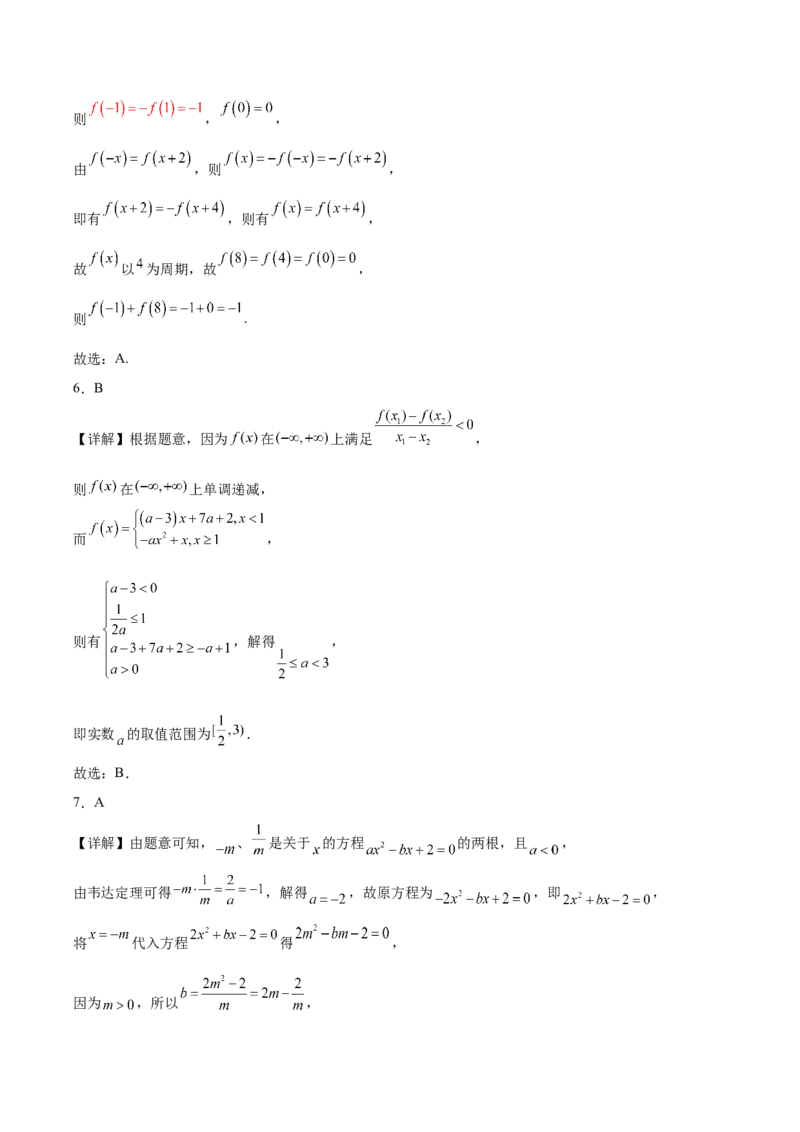文档内容
山东省德州市五校2025-2026学年高一上学期11月联考
数学试题
一、单选题
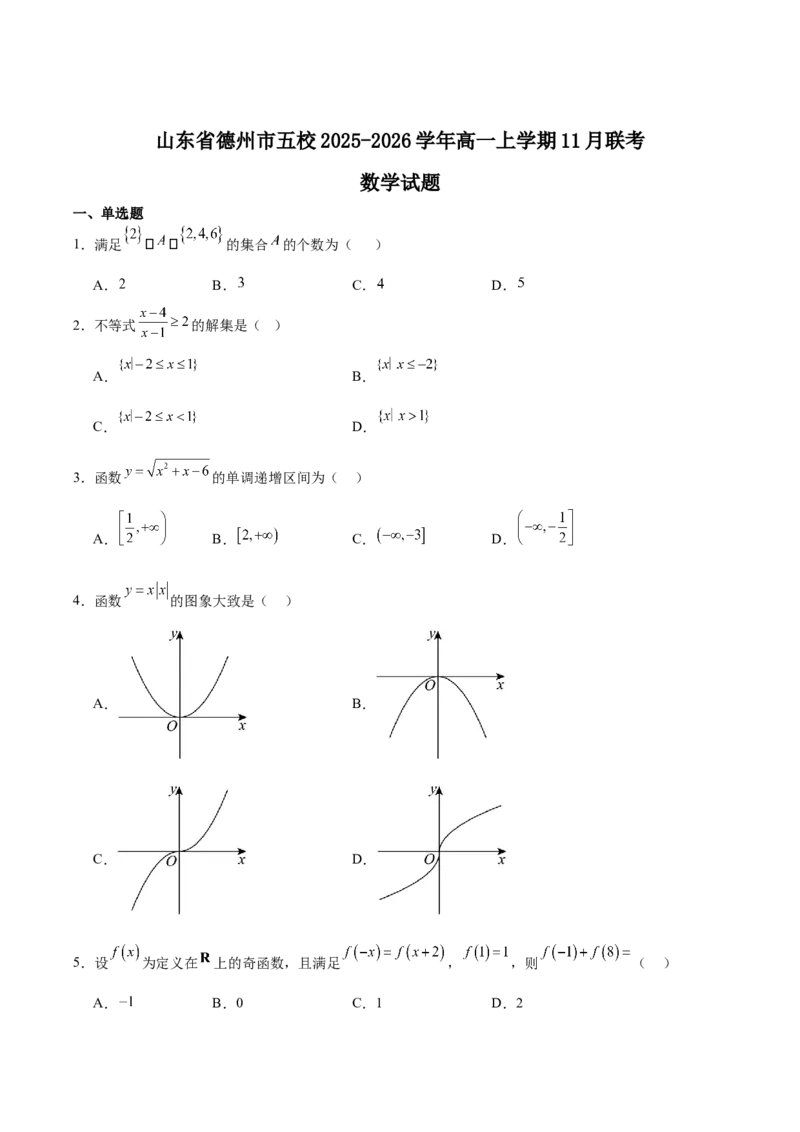
1.满足 的集合 的个数为( )
A. B. C. D.
2.不等式 的解集是( )
A. B.
C. D.
3.函数 的单调递增区间为( )
A. B. C. D.
4.函数 的图象大致是( )
A. B.
C. D.
5.设 为定义在 上的奇函数,且满足 , ,则 ( )
A. B.0 C.1 D.26.已知 在 上满足 ,则实数 的取值范围为( )
A. B. C. D.
7.已知关于 的不等式 的解集为 ,其中 ,则 的最小值为
( )
A. B. C. D.
8.已知函数 ,若存在四个不相等的实数 使得
,则 的取值范围是( )
A. B. C. D.
二、多选题
9.以下四个命题中,是真命题的有( )
A.
B.“ ”是“ ”的必要不充分条件
C.若 ,则
D.若命题 ,则 的否定为:
10.设正实数 满足 ,则( )
A. 有最大值为
B. 有最大值为C. 有最小值为5
D. 有最小值为
11.德国著名数学家狄利克雷(Dirichlet,1805~1859)在数学领域成就显著.19世纪,狄利克雷定义了一
个“奇怪的函数” 其中 为实数集, 为有理数集.则关于函数 有如下四个命
题,正确的为( )
A.对任意 ,都有
B.对任意 ,都存在 ,
C.若 , ,则有
D.存在三个点 , , ,使 为等腰直角三角形
三、填空题
12.函数 的定义域是 .
13.已知 ,则 的取值范围为 .
14.已知定义在R上的函数 在区间 上单调递增,若函数 为偶函数,且 ,则不
等式 的解集为
四、解答题
15.已知函数 .
(1)若函数 在区间 上是单调递增函数,求实数 的取值范围;(2)若 对一切实数 都成立,求实数 的取值范围.
16.已知集合 .
(1)当 时,求 ;
(2)若 ,求 的取值范围.
17.函数 为定义在 上的奇函数, 已知当 时, .
(1)当 时,求 的解析式;
(2)判断 在 上的单调性,并利用单调性的定义证明;
(3)若 ,求a的取值范围.
18.某公司每月生产某种电子仪器的固定成本为20000元,每生产一台仪器需增加投入100元,公司每月
生产量为 (单位:台),已知总收入 (单位:元)满足函数:
(1)将每月投入的成本 表示为月产量 的函数;
(2)将每月利润 表示为月产量 的函数;
(3)当月产量为何值时,公司所获利润最大?最大利润为多少万元?如果你是公司董事长,你应该确定月产
量为多少台?(总收入=总成本+利润)
19.已知函数 , .
(1)讨论函数 在 的单调性;
(2)若存在实数 , ,使得函数 的定义域为 时,值域为 ,求实数 的取值范围;
(3)若存在 ,使得 ,记 ,求 的最大值.参考答案
1.A
【详解】 为 的真子集, ,又 为 的真子集,
集合 中含有元素 或 ,但不同时包含 两个元素, 或 ,
满足题意的集合 的个数为 .
故选:A.
2.C
【详解】 即为 即 ,故 ,
故解集为 .
故选:C.
3.B
【详解】由题意可得 ,解得 或 ,
又 的单调递增区间为 ,
在 上单调递增,
故函数 的单调递增区间为 .
故选:B.
4.C
【详解】函数 的定义域为 ,且 ,即函数 是奇函数,
其图象关于原点对称,排除AB;
当 时, ,其图象是开口向上的抛物线 在 轴右侧部分,排除D,C满足.
故选:C
5.A
【详解】由 为定义在 上的奇函数,则 ,则 , ,
由 ,则 ,
即有 ,则有 ,
故 以 为周期,故 ,
则 .
故选:A.
6.B
【详解】根据题意,因为 在 上满足 ,
则 在 上单调递减,
而 ,
则有 ,解得 ,
即实数 的取值范围为 .
故选:B.
7.A
【详解】由题意可知, 、 是关于 的方程 的两根,且 ,
由韦达定理可得 ,解得 ,故原方程为 ,即 ,
将 代入方程 得 ,
因为 ,所以 ,所以 ,
当且仅当 时,即当 时,等号成立,
故 的最小值为 .
故选:A.
8.D
【详解】如图所示,
,
设 , ,
则 , , 是方程 ,即 的两个正根,所以 ,
令 ,解得 或 ,
所以 ,由题意 ,
所以 的取值范围是 .
故选:D.
9.ABD
【详解】对于A: ,故A是真命题;
对于B:因为 是 的真子集,
所以“ ”是“ ”的必要不充分条件,故B为真命题;
对于C:若 ,则 ,故C为假命题;
对于D:根据存在量词命题的否定,可知 的否定为: , ,故D为真命题.故选:ABD
10.ACD
【详解】对于A,因为 ,且 ,
所以 ,当且仅当 时等号成立,故A正确;
对于D,因为 又因为 ,
所以 ,
当且仅当 时等号成立,故D正确;
对于C,由 ,可得 ,
当且仅当 ,即 时等号成立,故C正确;
对于B,设 ,则
,当 取最大值时,即 最大,
将 代入,得 ,
因为 ,所以 ,
所以 ,所以 ,所以 ,
所以 的最大值取不到 ,故B错误.
故选:ACD.
11.BC
【详解】解:对于A选项,当 ,则 ,此时 ,故A选项错误;
对于B选项,当任意 时,存在 ,则 ,故 ;当任意 时,存在 ,则 ,故 ,故对任意 ,都存在 ,
成立,故B选项正确;
对于C选项,根据题意得函数 的值域为 ,当 , 时, ,
故C选项正确;
对于D选项,要为等腰直角三角形,只可能为如下四种情况:
①直角顶点 在 上,斜边在 轴上,此时点 ,点 的横坐标为无理数,则 中点的横坐标仍然为
无理数,那么点 的横坐标也为无理数,这与点 的纵坐标为1矛盾,故不成立;
②直角顶点 在 上,斜边不在 轴上,此时点 的横坐标为无理数,则点 的横坐标也应为无理数,
这与点 的纵坐标为1矛盾,故不成立;
③直角顶点 在 轴上,斜边在 上,此时点 ,点 的横坐标为有理数,则 中点的横坐标仍然为
有理数,那么点 的横坐标也应为有理数,这与点 的纵坐标为0矛盾,故不成立;
④直角顶点 在 轴上,斜边不在 上,此时点 的横坐标为无理数,则点 的横坐标也应为无理数,这与点 的纵坐标为1矛盾,故不成立.
综上,不存在三个点 , , ,使得 为等腰直角三角形,故选项
D错误.
故选:BC.
12.
【详解】由已知,若函数有意义,则 ,解得 ,
即 ,
故答案为: .
13.
【详解】依题意, ,
由 ,得 ,而 ,
因此 ,即 ,
所以 的取值范围是 .
故答案为:
14.
【详解】因为 定义域为R,且 为偶函数,则 ,
所以 的图象关于直线 对称,因为 ,则 ,
根据已知区间单调性和对称性: 时, 得 , 时, 得 ,综上,不等式 的解集为 .
故答案为:
15.(1)
(2)
【详解】(1)因为函数 在区间 上是单调递增函数,
且 的对称轴为 ,
所以 ,解得 .
(2)若 对一切实数 都成立,
则 ,解得 .
16.(1) 或 .
(2) 或 .
【详解】(1) ,
当 时, ,因为 ,
所以 或 ,
所以 或 .
(2)因为 ,所以 .
当 时, ,解得 ;
当 时, ,解得 .
由 ,得 解得 .
综上, 的取值范围为 或 .17.(1) 时, ;
(2)单调递增,证明见解析;
(3) .
【详解】(1)当 时, ,则 ,
因为函数为奇函数,所以 ,
即 时, 的解析式为 ;
(2) 在 上的单调递增,
证明如下:
任取 , ,且 ,则 ,
因为 , ,且 ,所以 , , ,
则 ,即 ,
所以 在 上的单调递增;
(3) 在 上的单调递增,且函数 为 上的奇函数,故 为 上的增函数.
由 , ,
于是 ,解得 ,即所求为 .
18.(1) ;
(2)(3)500台,5万元,500台.
【详解】(1)依题意,每月投入的成本 与月产量 的函数关系为: .
(2)由(1)及 ,
得利润 .
(3)由(2)知,当 时, ,
则当 时,利润 取得最大值5000;
当 时, ,
当且仅当 时,利润 取得最大值50000,而 ,
所以当月产量为500台时,公司所获利润最大值为5万元,应当应该确定月产量为500台.
19.(1)答案见解析
(2)
(3)
【详解】(1) ,
任取 ,则
①当 时, , ,所以 ,所以 ,所以 ,即 ,
所以 在 上单调递减.
②当 时, , ,所以 在 上单调递增.
(2) ,显然函数 在 上单调递增,
所以当 时函数 在 上单调递增,
所以由题意可得 ,所以 ,
所以 、 是方程 的两个实数根,
即关于 的方程 在 上有两个不等的实数根,
设 ,显然函数 过点 ,
所以 ,解得 ,
所以实数 的取值范围 ;
(3)由(1)可知 在 上单调递减.
若 ,此时 ,不满足题意;
故必有 ,于是 ,所以 ,
整理得: (当 时不成立),记函数 ,则方程 在 上有解,
函数 开口向上,对称轴为 ,
于是 在 上单调递增,为使 有解,则 .