文档内容
格致课堂
第八章 章末测试题
一、选择题
1.如图所示, ,则平面 与平面 的交线是(
)
A.直线 B.直线 C.直线 D.直线
【答案】C
【解析】由题意知, , ,∴ ,又∵ ,∴ 平面 ,即 在平面 与
平面 的交线上,又 平面 , ,∴点 在平面 与平面 的交线上,
∴平面 平面 ,故选 .
2.正方体内切球与外接球体积之比为 ( )
A.1∶ B.1∶3 C.1∶3 D.1∶9
【答案】C
【解析】
设正方体的棱长为a,则它的内切球的半径为 a,它的外接球的半径为 a,故所求体积之比为1︰3
.
故答案为C.
3.已知三棱锥 的所有顶点都在球 的求面上, 是边长为 的正三角形, 为球 的直格致课堂
径,且 ,则此棱锥的体积为( )
A. B. C. D.
【答案】A
【解析】根据题意作出图形:
设球心为O,过ABC三点的小圆的圆心为O,则OO ⊥平面ABC,
1 1
延长CO 交球于点D,则SD⊥平面ABC.∵CO= ,
1 1
∴ ,
∴高SD=2OO = ,∵△ABC是边长为1的正三角形,∴S = ,
1 ABC
△
∴ .
4.设 是两条不同的直线, 是两个不同的平面,则下列命题正确的是( )
A.若 , ,则 B.若 , ,则
C.若 , , ,则 D.若 , , ,则
【答案】C
【解析】对于 ,当 为 内与 垂直的直线时,不满足 , 错误;
对于 ,设 ,则当 为 内与 平行的直线时, ,但 , 错误;格致课堂
对于 ,由 , 知: ,又 , , 正确;
对于 ,设 ,则当 为 内与 平行的直线时, , 错误.
故选: .
5.已知直线a,b分别在两个不同的平面 , 内 则“直线a和直线b相交”是“平面 和平面 相交”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
【答案】A
【解析】当“直线a和直线b相交”时,平面α和平面β必有公共点,即平面α和平面β相交,充分性成立;
当“平面α和平面β相交”,则 “直线a和直线b可以没有公共点”,即必要性不成立.
故选A.
6.如图所示,在长方体 中, ,则 与平面 所成角
的正弦值为( )
A. B. C. D.
【答案】D
A B C D
【解析】如图所示,在平面 1 1 1 1内过点 作 的垂线,垂足为 ,连接 .
平面 , 的正弦值即为所求. ,格致课堂
, .
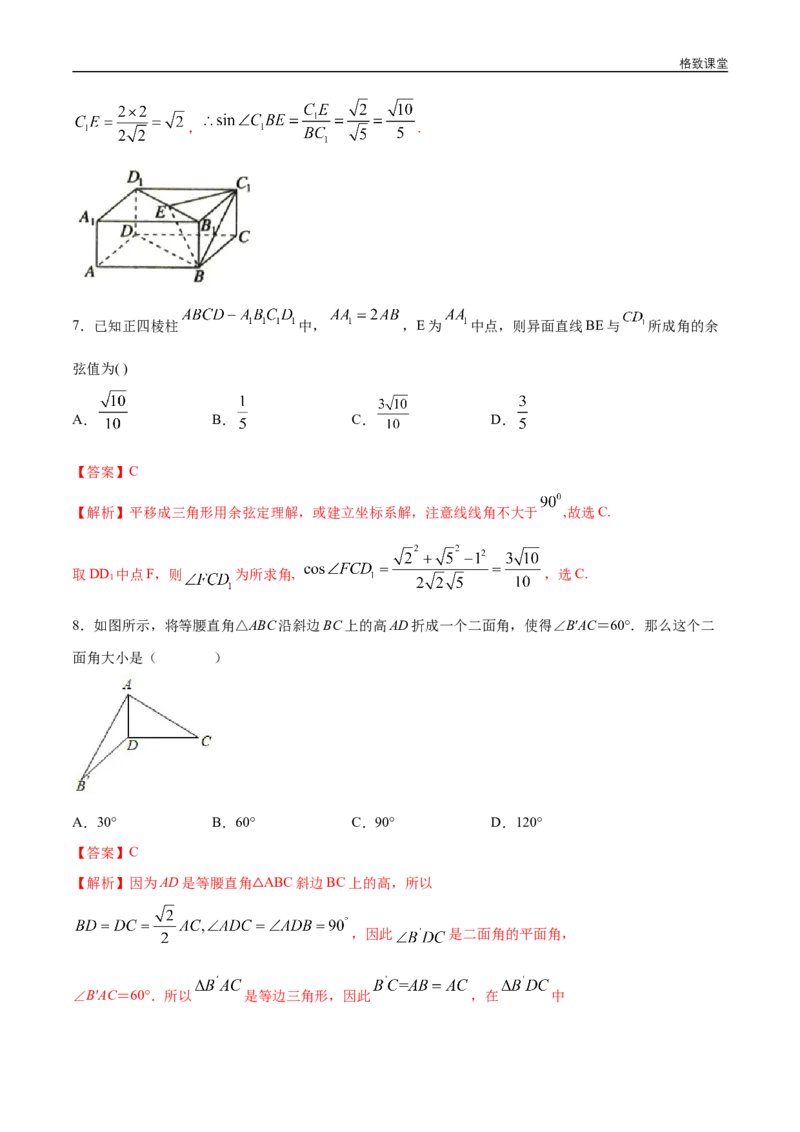
7.已知正四棱柱 中, ,E为 中点,则异面直线BE与 所成角的余
弦值为( )
A. B. C. D.
【答案】C
【解析】平移成三角形用余弦定理解,或建立坐标系解,注意线线角不大于 ,故选C.
取DD 中点F,则 为所求角, ,选C.
1
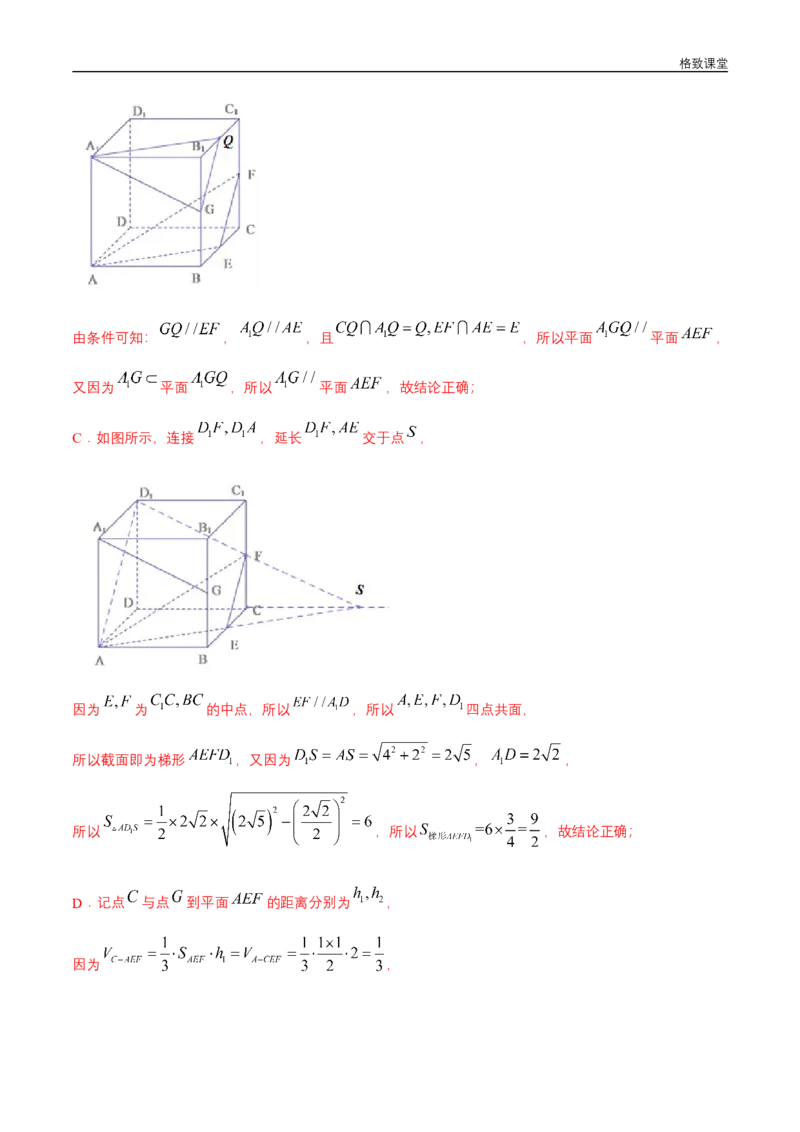
8.如图所示,将等腰直角△ABC沿斜边BC上的高AD折成一个二面角,使得∠B′AC=60°.那么这个二
面角大小是( )
A.30° B.60° C.90° D.120°
【答案】C
【解析】因为AD是等腰直角 ABC斜边BC上的高,所以
△
,因此 是二面角的平面角,
∠B′AC=60°.所以 是等边三角形,因此 ,在 中格致课堂
.
故选:C
二、多选题
9.下列命题为真命题的是( )
A.若两个平面有无数个公共点,则这两个平面重合
B.若一个平面经过另一个平面的垂线,那么这两个平面相互垂直
C.垂直于同一条直线的两条直线相互平行
D.若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面不垂直
【答案】BD
【解析】A错,两个平面相交时,也有无数个公共点;
B选项就是面面垂直的判定定理,正确;
C错,比如 , , ,显然有 , ,但b与c也可能相交;
D利用反证法证明,假设这条直线与另一个平面垂直,则这条直线垂直于平面内的任何一条直线,当然就
垂直于这条交线,与已知条件矛盾,所以原说法正确.
故选:BD.
10.如图,在棱长均相等的四棱锥 中, 为底面正方形的中心, , 分别为侧棱 , 的中
点,有下列结论正确的有:( )
A. ∥平面 B.平面 ∥平面
C.直线 与直线 所成角的大小为 D.
【答案】ABD
【解析】选项A,连接BD,显然O为BD的中点,又N为PB的中点,所以 ∥ON,由线面平行的判定定
理可得, ∥平面 ;选项B, 由 , 分别为侧棱 , 的中点,得MN∥AB,又底面为正方形,格致课堂
所以MN∥CD,由线面平行的判定定理可得,CD∥平面OMN,又选项A得 ∥平面 ,由面面平行
的判定定理可得,平面 ∥平面 ;选项C,因为MN∥CD,所以∠ PDC为直线 与直线
所成的角,又因为所有棱长都相等,所以∠ PDC= ,故直线 与直线 所成角的大小为 ;选
项D,因底面为正方形,所以 ,又所有棱长都相等,所以 ,故
,又
∥ON,所以 ,故ABD均正确.
11、正方体 的棱长为2, 分别为 的中点,则( )
A.直线 与直线 垂直 B.直线 与平面 平行
C.平面 截正方体所得的截面面积为 D.点 与点 到平面 的距离相等
【答案】BC
【解析】A.若 ,又因为 且 ,所以 平面 ,
所以 ,所以 ,显然不成立,故结论错误;
B.如图所示,取 的中点 ,连接 ,格致课堂
由条件可知: , ,且 ,所以平面 平面 ,
又因为 平面 ,所以 平面 ,故结论正确;
C.如图所示,连接 ,延长 交于点 ,
因为 为 的中点,所以 ,所以 四点共面,
所以截面即为梯形 ,又因为 , ,
所以 ,所以 ,故结论正确;
D.记点 与点 到平面 的距离分别为 ,
因为 ,格致课堂
又因为 ,
所以 ,故结论错误.
故选:BC.
12.正方体 的棱长为2,已知平面 ,则关于 截此正方体所得截面的判断正
确的是( )
A.截面形状可能为正三角形 B.截面形状可能为正方形
C.截面形状可能为正六访形 D.截面面积最大值为
【答案】ACD
【解析】如图,显然A,C成立,下面说明D成立,
如图设截面为多边形 ,
设 ,则 ,
则
所以多边形 的面积为两个等腰梯形的面积和,
所以
因为 ,格致课堂
,
所以
当 时, ,故D成立。
故选:ACD.
三、填空题
13.一个圆柱的侧面展开图是一个边长为1的正方形,则该圆柱的体积是____.
【答案】
【解析】依题意可得,圆柱的高为1,底面周长为1,则底面半径为 ,
所以圆柱体积为 .
故答案为: .
14.如图,在正方体ABCD-ABC D 中,AB=2,点E为AD的中点,点F在CD上.若EF∥平面ABC,
1 1 1 1 1
则线段EF的长度等于________.
【答案】
【解析】如图:格致课堂
因为 平面 , 平面 ,且平面 平面 ,
所以 ,
又因为 为 的中点,所以 为 的中点,
所以 ,
因为正方体的棱长为2.所以 ,
所以 .
故答案为: .
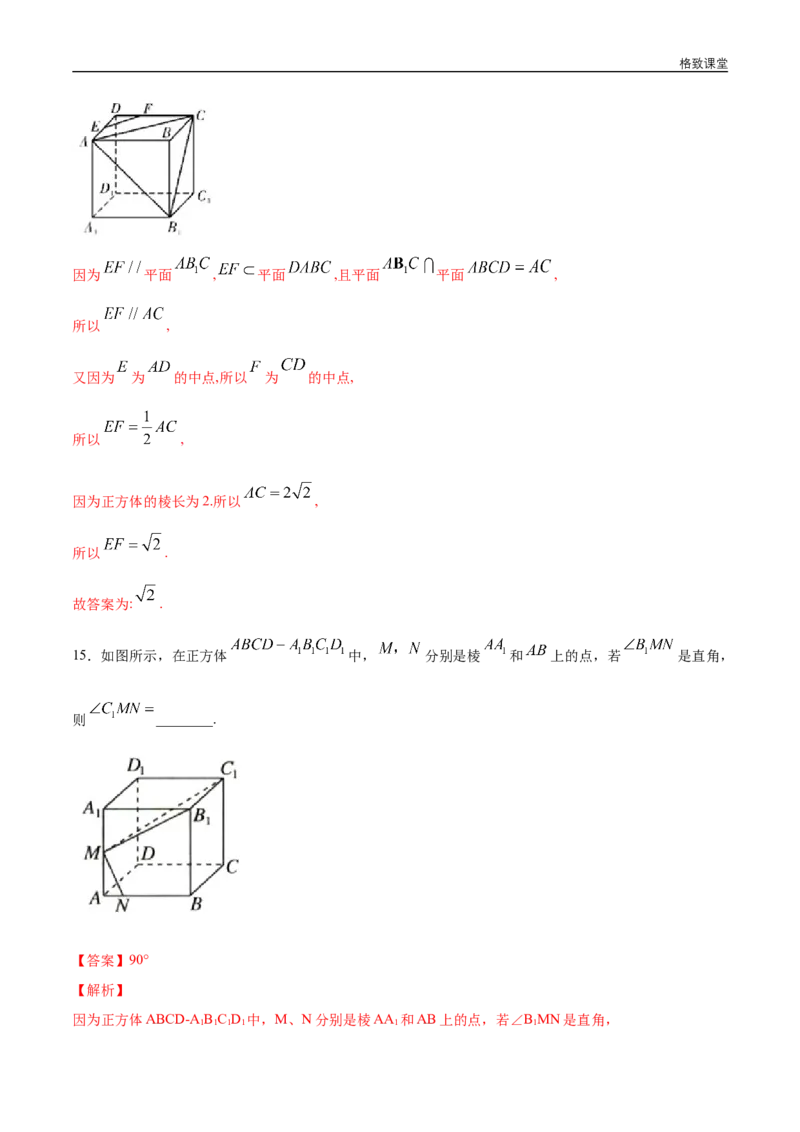
15.如图所示,在正方体 中, 分别是棱 和 上的点,若 是直角,
则 ________.
【答案】90°
【解析】
因为正方体ABCD-A B C D 中,M、N分别是棱AA 和AB上的点,若∠B MN是直角,
1 1 1 1 1 1格致课堂
所以MN⊥MB ,因为B C 是棱,所以MN⊥B C ,所以MN⊥平面MB C ,
1 1 1 1 1 1 1
所以∠C MN=90°
1
故答案为90°
16.在棱长为a的正方体ABCDABC D 中,EF是棱AB上的一条线段,且EF=b(b