文档内容
格致课堂
第八章 立体几何初步
一、单选题
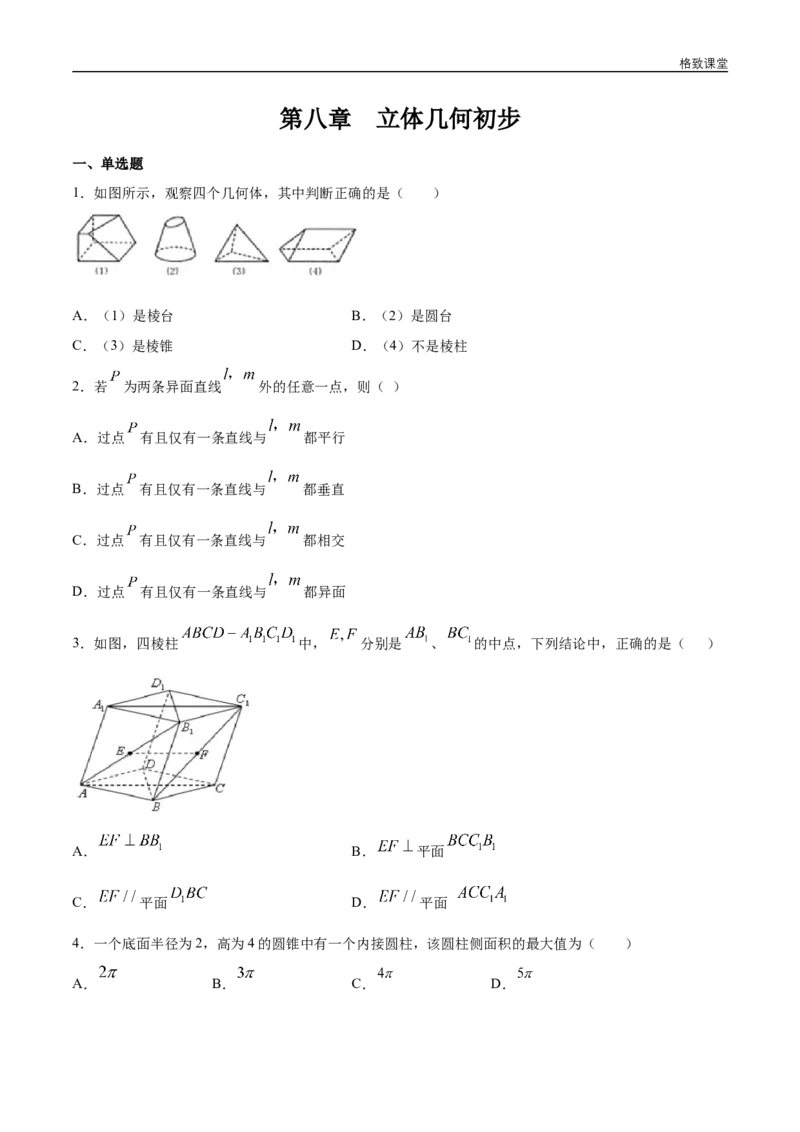
1.如图所示,观察四个几何体,其中判断正确的是( )
A.(1)是棱台 B.(2)是圆台
C.(3)是棱锥 D.(4)不是棱柱
2.若 为两条异面直线 外的任意一点,则( )
A.过点 有且仅有一条直线与 都平行
B.过点 有且仅有一条直线与 都垂直
C.过点 有且仅有一条直线与 都相交
D.过点 有且仅有一条直线与 都异面
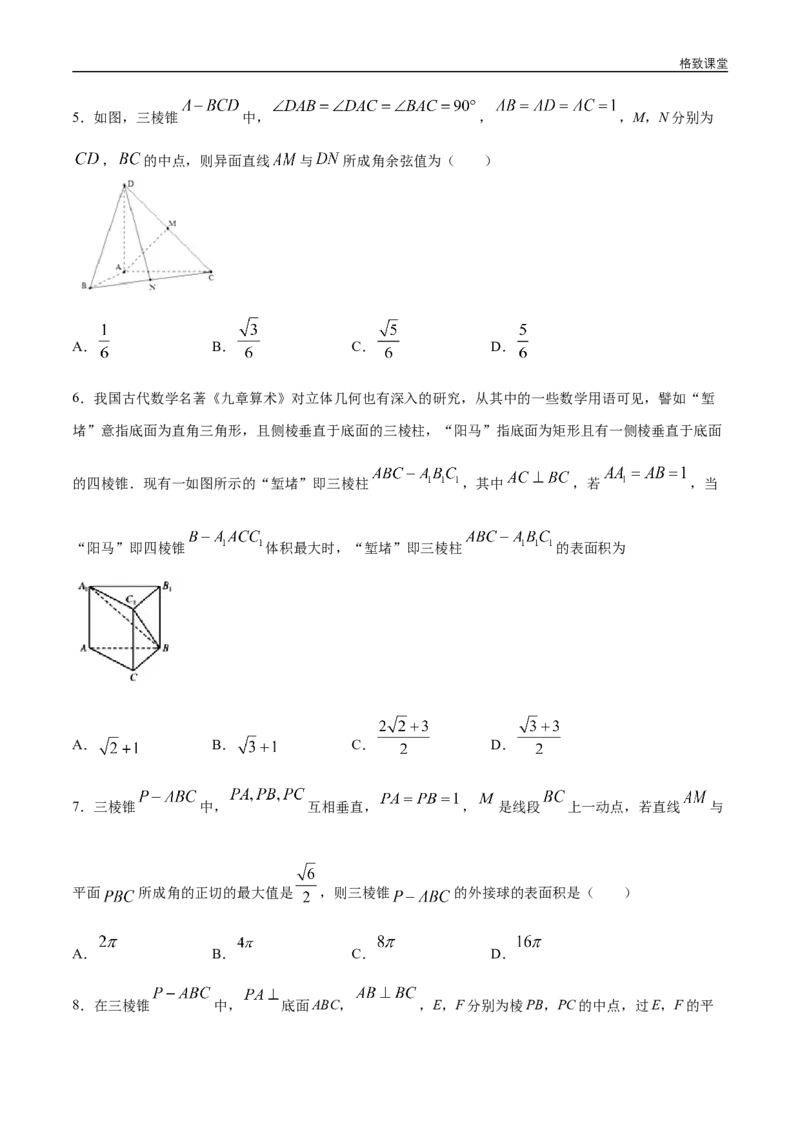
3.如图,四棱柱 中, 分别是 、 的中点,下列结论中,正确的是( )
A. B. 平面
C. 平面 D. 平面
4.一个底面半径为2,高为4的圆锥中有一个内接圆柱,该圆柱侧面积的最大值为( )
A. B. C. D.格致课堂
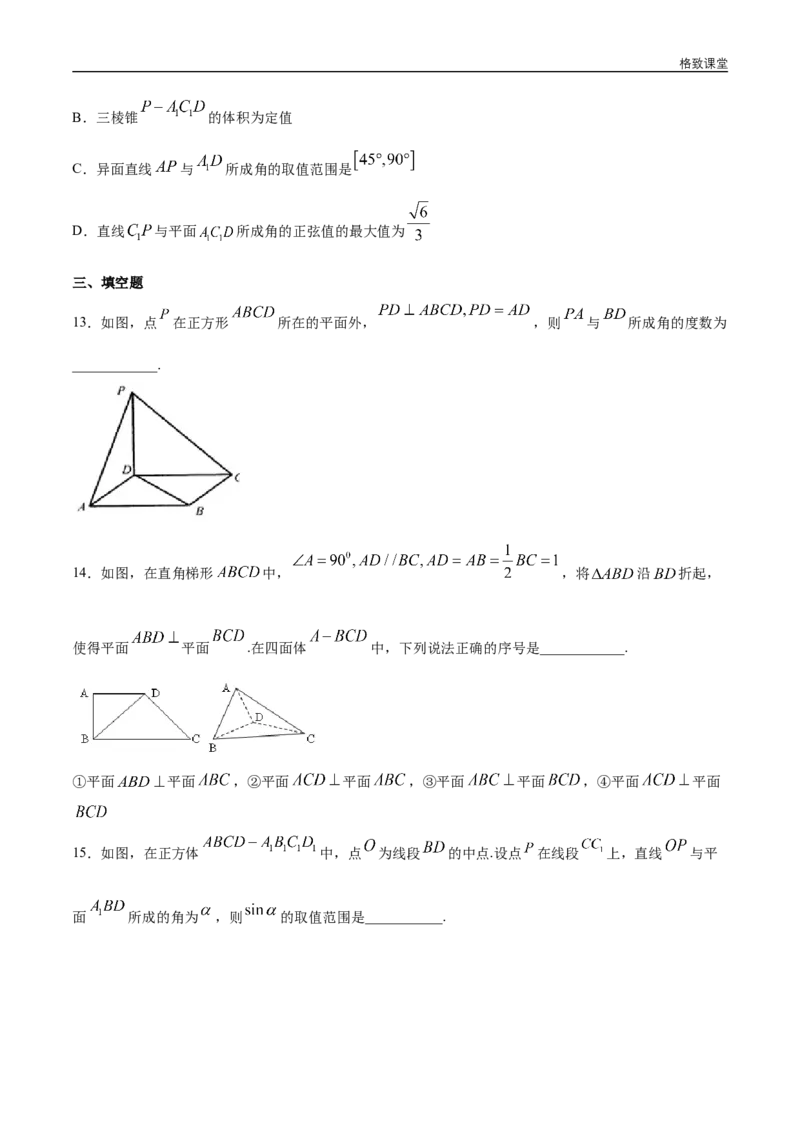
5.如图,三棱锥 中, , ,M,N分别为
, 的中点,则异面直线 与 所成角余弦值为( )
A. B. C. D.
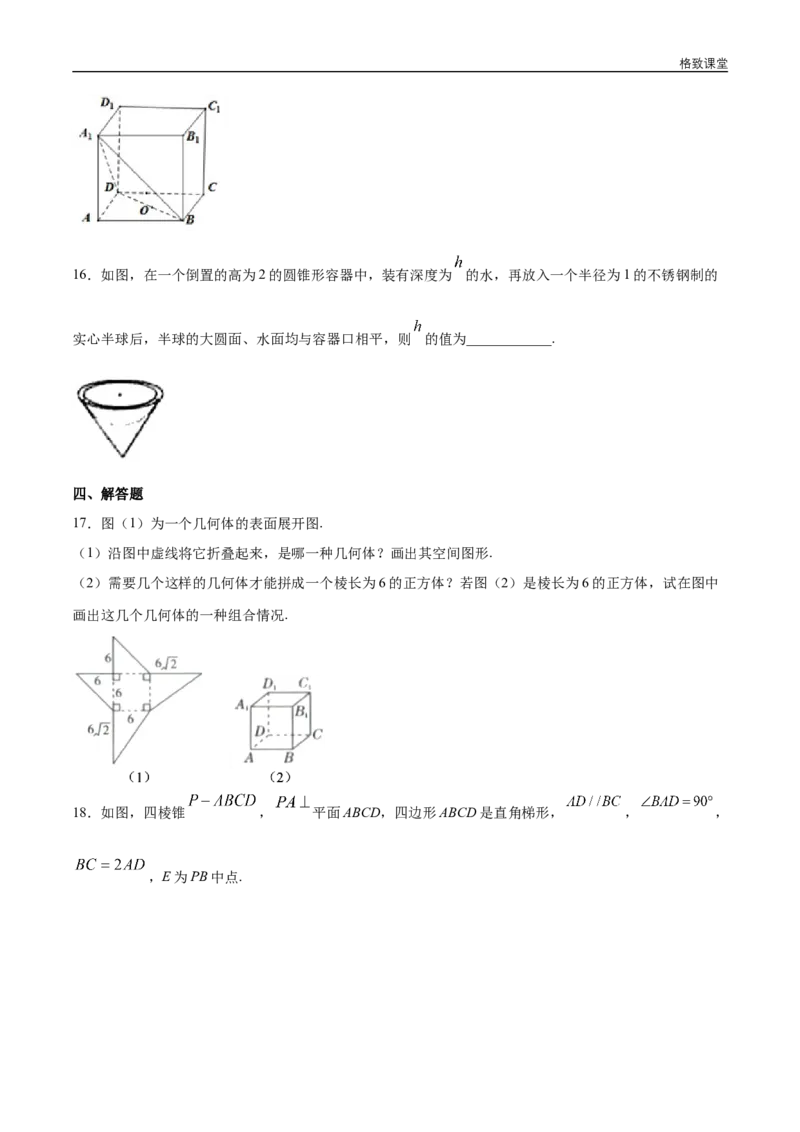
6.我国古代数学名著《九章算术》对立体几何也有深入的研究,从其中的一些数学用语可见,譬如“堑
堵”意指底面为直角三角形,且侧棱垂直于底面的三棱柱,“阳马”指底面为矩形且有一侧棱垂直于底面
的四棱锥.现有一如图所示的“堑堵”即三棱柱 ,其中 ,若 ,当
“阳马”即四棱锥 体积最大时,“堑堵”即三棱柱 的表面积为
A. B. C. D.
7.三棱锥 中, 互相垂直, , 是线段 上一动点,若直线 与
平面 所成角的正切的最大值是 ,则三棱锥 的外接球的表面积是( )
A. B. C. D.
8.在三棱锥 中, 底面ABC, ,E,F分别为棱PB,PC的中点,过E,F的平格致课堂
面分别与棱AB,AC相交于点D,G,给出以下四个结论:
① ;② ;③ ;④ .
则以上正确结论的个数是
A.1 B.2 C.3 D.4
二、多选题
9.已知两条直线 , 及三个平面 , , ,则 的充分条件是( ).
A. , B. , ,
C. ,β∥γ D. , ,
10.在正四面体 中, 、 、 分别是 、 、 的中点,下面四个结论中正确的是( )
A. 平面 B. 平面
C.平面 平面 D.平面 平面
11.在三棱锥D-ABC中, ,且 , ,M,N分别是棱BC,
CD的中点,下面结论正确的是( )
A. B. 平面ABD
C.三棱锥A-CMN的体积的最大值为 D.AD与BC一定不垂直
12.如图,在正方体 中,点 在线段 上运动,则 ( )
A.直线 平面格致课堂
B.三棱锥 的体积为定值
C.异面直线 与 所成角的取值范围是
D.直线 与平面 所成角的正弦值的最大值为
三、填空题
13.如图,点 在正方形 所在的平面外, ,则 与 所成角的度数为
____________.
14.如图,在直角梯形 中, ,将 沿 折起,
使得平面 平面 .在四面体 中,下列说法正确的序号是____________.
①平面 平面 ,②平面 平面 ,③平面 平面 ,④平面 平面
15.如图,在正方体 中,点 为线段 的中点.设点 在线段 上,直线 与平
面 所成的角为 ,则 的取值范围是___________.格致课堂
16.如图,在一个倒置的高为2的圆锥形容器中,装有深度为 的水,再放入一个半径为1的不锈钢制的
实心半球后,半球的大圆面、水面均与容器口相平,则 的值为____________.
四、解答题
17.图(1)为一个几何体的表面展开图.
(1)沿图中虚线将它折叠起来,是哪一种几何体?画出其空间图形.
(2)需要几个这样的几何体才能拼成一个棱长为6的正方体?若图(2)是棱长为6的正方体,试在图中
画出这几个几何体的一种组合情况.
18.如图,四棱锥 , 平面ABCD,四边形ABCD是直角梯形, , ,
,E为PB中点.格致课堂
(1)求证: 平面PCD;
(2)求证: .
19.如图所示,已知 平面 , , 分别是 , 的中点, .
(1)求证: 平面 ;
(2)求证:平面 平面 ;
(3)若 , ,求直线 与平面 所成的角.
20.如图,四棱锥 中,底面 为矩形, 面 , 为 的中点.
(1)证明: 平面 ;
(2)设 , ,三棱锥 的体积 ,求A到平面PBC的距离.格致课堂
21 . 如 图 , 在 四 棱 锥 中 , 底 面 , , ,
, ,点 为棱 的中点.
(Ⅰ)证明: ;
(Ⅱ)求直线 与平面 所成角的正切值.
22.如图,在四棱锥 中,底面 为平行四边形,点 在面 内的射影为 ,
,点 到平面 的距离为 ,且直线 与 垂直.
(Ⅰ)在棱 上找一点 ,使直线 与平面 平行,并说明理由;
(Ⅱ)在(Ⅰ)的条件下,求二面角 的大小.