文档内容
枣庄三中 ~ 学年度⾼⼀年级学情调查考试
2025 2026
数学试题
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(⾮选择题)两部分。满分150分,考试⽤时120分钟。答卷前,
考⽣务必将⾃⼰的姓名、准考证号、考试科⽬填涂在答题卡和答题纸规定的地⽅。
第 Ⅰ 卷(选择题 共 58 分)
⼀、单项选择题(共8⼩题,每⼩题5分,共40分.在每题给出的四个选项中,只有⼀项是符合题⽬要求
的.)
1. 已知集合 , ,则( )
A. B. C. D.
2.“ ”是“ 的终边落在第⼀象限或落在第四象限”的( )
A.充分不必要条件 B.必要不充分条件 C.既不充分⼜不必要条件 D. 充要条件
3. 若 ,则 ( )
A. B. C. D.
4.已知函数 的图象是⼀条连续不断的曲线,且有如下对应值表:
1 2 3 4 5 6
﹣6.136 15.552 ﹣3.92 10.88 ﹣52.488 ﹣232.064
则函数 ⾄少有⼏个零点( )
A.1. B.2 C.3 D.4
5. 已知 ,则 ( )
A.2 B. C. D.
6. 已知 ,则( )
A. B. C. D.
7. 若函数 的值域为 ,且在区间 上单调递增,则实数 的取
值范围是( )
第 1 ⻚ 共 5 ⻚
学科⽹(北京)股份有限公司A. B. C. D.
8.若函数 ,则函数 的值域为( )
A. B. C. D. ,2]
⼆、多选题(共3⼩题,每⼩题6分,共18分.在每⼩题给出的选项中,⾄少有两项是符合题⽬要求的.
若全部选对得6分,部分选对得部分分,选错或不选得0分.)
9. 以下说法正确的是( )
A. 与 是同⼀个函数.
B.函数 的值域为 .
C. 过定点 ,则 9.
D. 函数 的最⼩值为6.
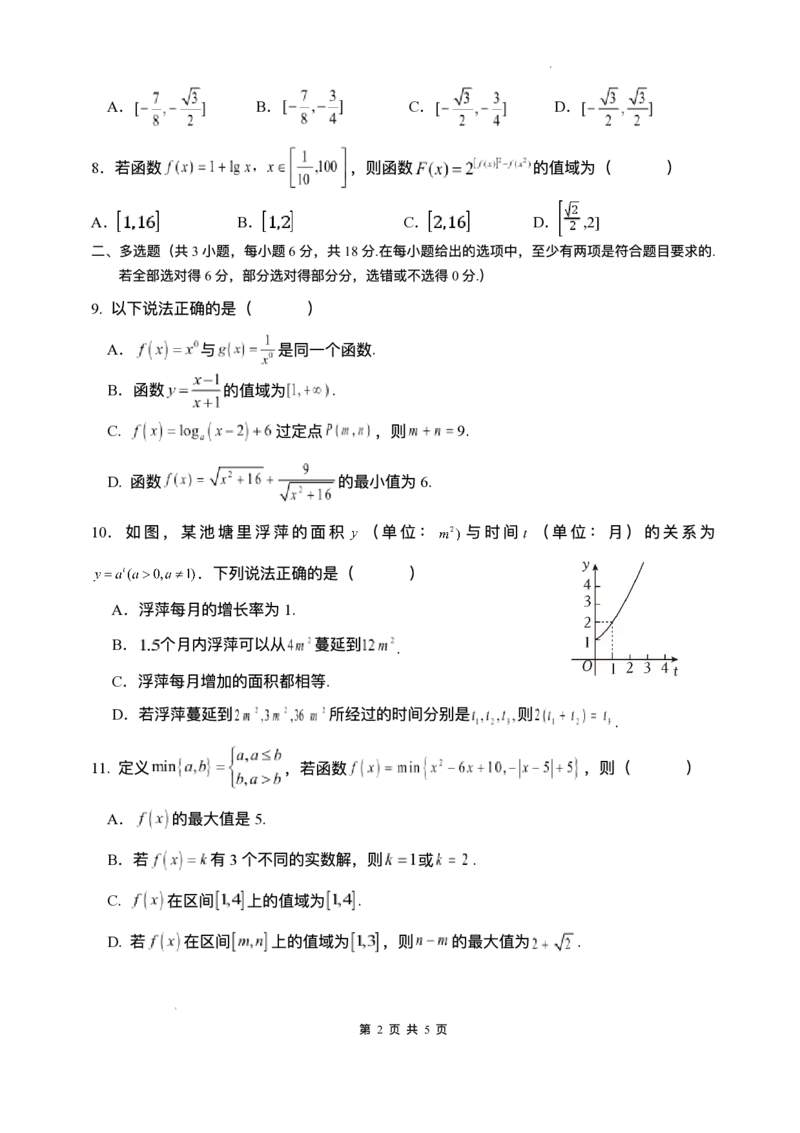
10.如图,某池塘⾥浮萍的⾯积 (单位: 与时间 (单位:⽉)的关系为
.下列说法正确的是( )
A.浮萍每⽉的增⻓率为1.
B. 个⽉内浮萍可以从 蔓延到
.
C.浮萍每⽉增加的⾯积都相等.
D.若浮萍蔓延到 所经过的时间分别是 则
.
11. 定义 ,若函数 ,则( )
A. 的最⼤值是5.
B.若 有3个不同的实数解,则 或 .
C. 在区间 上的值域为 .
D. 若 在区间 上的值域为 ,则 的最⼤值为 .
第 2 ⻚ 共 5 ⻚
学科⽹(北京)股份有限公司第 Ⅱ 卷(⾮选择题 共 92 分)
三、填空题(共3⼩题,每⼩题5分,满分15分.)
12. 若已知 ,且 ,则 .
13. 已知扇形的周⻓为20,则扇形⾯积取到最⼤值时圆⼼⻆的弧度数是 .
14. 借助信息技术计算 的值,我们发现当 …时,
的底数越来越⼩,⽽指数越来越⼤,随着 越来越⼤, 会⽆限趋近于 ,根据
以上知识判断,当 越来越⼤时, 会趋近于 .
四、解答题(共5⼩题,满分77分.解答应写出⽂字说明、证明过程或演算步骤.)
15. (13分)
(1)已知 ,求 的值;
(2)求值: ;
16. (15分)
已知幂函数 的图象关于 轴对称.
(1)求 的值及函数 的解析式;
(2)设函数 在区间 , 上的最⼩值为2,求实数 的值.
第 3 ⻚ 共 5 ⻚
学科⽹(北京)股份有限公司17. (15分)
在某种药物研究试验中发现其在⾎液内的浓度 (单位:毫克/毫升)与时间 (单位:
⼩时)满⾜函数关系 ,其中 , 为⼤于 的常数.已知该药物在⾎
液内的浓度是⼀个连续变化的过程,且在 ⼩时时达到最⼤值 毫克/毫升.
(1)求实数 , 的值;
(2)当该药物浓度不⼩于最⼤值的⼀半时,称该药物有效.求该药物有效的时间⻓度 (单
位:⼩时).
18. (17分)
已知定义在 上的函数 满⾜:对任意的实数 ,均有 ,且
,当 时, .
(1)判断 的奇偶性并证明;
(2)判断 在 上的单调性,并证明;
(3)若对任意 ,总有 恒成⽴,求实数
的取值范围.
19. (17分)
已知函数 .
(1)若 ,求函数 在区间 上的值域;
(2)若 ,求 的值;
第 4 ⻚ 共 5 ⻚
学科⽹(北京)股份有限公司(3)令 ,则 ,已知函数 在区间 上有零点,
求实数 的取值范围.
第 5 ⻚ 共 5 ⻚
学科⽹(北京)股份有限公司枣庄三中2025~2026学年度⾼⼀年级学情调查考试
数学试题答案
⼀、选择题1. B.2. C.3. A.4.D 5.B 6. B. 7. A.8.B 9.AC 10. AD. 11.ABD
三、填空12. .13. 2 14.e4
14.解:根据题意,(1+ )2n=(1+ )2n=[(1+ ]4,由于随着n越来越⼤, 会⽆限趋近
于e,则随着n越来越⼤,(1+ 会⽆限趋近于e,1+ 会⽆限趋近于1,故(1+ )2n+1=[(1+ ]4
会⽆限趋近于e4,故答案为:e4.
四、解答题
41516(1) , ……………3分
……………6分
所以 . ……………7分
(2)
. ……………13分
16. (1) 得 或 , ……………3分
⼜ 的图象关于 轴对称,则 ,此时 ; ……………4分
(2) ,易知⼆次函数 图象的开⼝向上,对称轴为 , ……………5分
当 ,即 时,函数 在区间 , 上单调递增,
则 (1) ,解得 ,⽭盾; ……………8分
当 ,即 时,函数 在区间 , 上单调递减,
则 (4) ,解得 ,⽭盾; ……………11分
当 ,即 时, ,解得 (负值舍去);…………14分
综上,实数 的值为 . ……………15分
第 1 ⻚第共 4 ⻚
学科⽹(北京)股份有限公司17.(1)因为该药物在⾎液内的浓度是⼀个连续变化的过程,
函数 在 时取最⼤值 ,
所以 , , ,
所以 , , ……………6分
(2)由(1) , ……………8分
令 可得,
若 ,则 ,解得 , ……………10分
若 ,则 ,解得 , ……………12分
综上: 的取值范围为 ……………14分
所以该药物有效的时间⻓度 为 (⼩时) ……………15分
18.(1)函数 为R上的奇函数. ……………1分
证明如下:易知函数 的定义域为 ,
令 ,则 ,⼜ ,
所以 ,所以函数 为奇函数. ……………3分
(2) 在 上的单调递增,证明如下:由(1)知, ,
当 时, ,所以 ,
从⽽ , ……………5分
,则
, ……………8分
第 2 ⻚第共 4 ⻚
学科⽹(北京)股份有限公司因为 ,所以 ,⼜当 时, ,
所以 ,所以 ,所以
故 在 上的单调递增. ……………10分
(3) 由(1)知,函数 为R上的奇函数,所以 , ……………11分
由(2)知,当 时, ,且 在 上的单调递增,
所以 在 上单调递增, ……………12分
所以当 时,函数 的最⼤值为 ,最⼩值为 ,
⼜任意 ,总有 恒成⽴,所以
, ……………14分
即 ,由题意, 对 恒成⽴,
令 ,则 , ……………15分
所以 ,解得 或 ,
故实数 的取值范围是 ……………17分
19(1). ……………2分
,当 时,函数 为增函数,
则函数 的最⼤值为 ,函数 的最⼩值为 ,
所以函数 的值域 . ……………4分
(2) ,则 ,
第 3 ⻚第共 4 ⻚
学科⽹(北京)股份有限公司, ……………7分
设 ,则
,
两式相加得 ,则 ,
故 ……………10分
(3) ,设 ,
当 时, ,则函数 等价于 ,
若函数 在区间 上有零点,
则等价于 在 上有零点, ……………12分
即 在区间 上有解,
所以, 在区间 上有解,
所以, , ……………14分
设 ,则 ,则 ,
因为函数 在区间 上单调递增,且 , ……………16分
当 时, ,所以 ,所以,实数 的取值范围是 .…………17分
第 4 ⻚第共 4 ⻚
学科⽹(北京)股份有限公司