文档内容
格致课堂
第十章 概率
一、单选题
1.某袋中有9个除颜色外其他都相同的球,其中有5个红球,4个白球,现从中任意取出1个,则取出的球恰好
是白球的概率为( )
A. B. C. D.
2.把红、黄、蓝、白4张纸牌随机分给甲、乙、丙、丁4个人,每人分得一张,事件“甲分得红牌”与事
件“乙分得红牌”是
A.对立事件 B.互斥但不对立事件
C.不可能事件 D.以上都不对
3.根据某教育研究机构的统计资料,在校学生近视的概率为40%,某眼镜商要到一中学给学生配眼镜,
若已知该校学生总人数为1200,则该眼镜商应准备眼镜的数目为( )
A.460 B.480 C.不少于480 D.不多于480
4.已知某运动员每次投篮命中的概率都为40%.现采用随机模拟的方法估计该运动员三次投篮恰有两次命
中的概率:先由计算器算出0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0
表示不命中;再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了20组随机数:
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
据此估计,该运动员三次投篮恰有两次命中的概率为( )
A.0.35 B.0.25 C.0.20 D.0.15
5.甲在微信群中发了一个6元“拼手气”红包,被乙、丙、丁三人抢完,若三人均领到整数元,且每人至少领到
1元,则乙获得“最佳手气”(即乙领到的钱数多于其他任何人)的概率是( )
A. B. C. D.
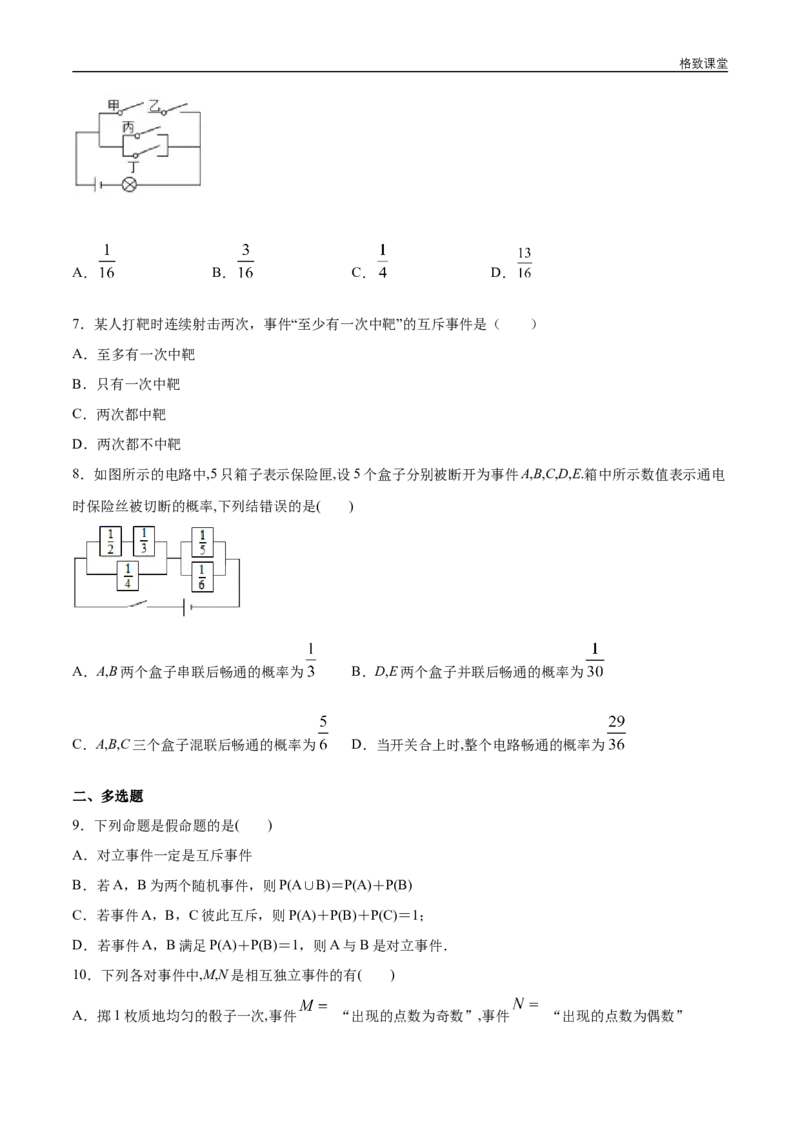
6.如图,已知电路中4个开关闭合的概率都是 ,且是相互独立的,则灯亮的概率为( )格致课堂
A. B. C. D.
7.某人打靶时连续射击两次,事件“至少有一次中靶”的互斥事件是( )
A.至多有一次中靶
B.只有一次中靶
C.两次都中靶
D.两次都不中靶
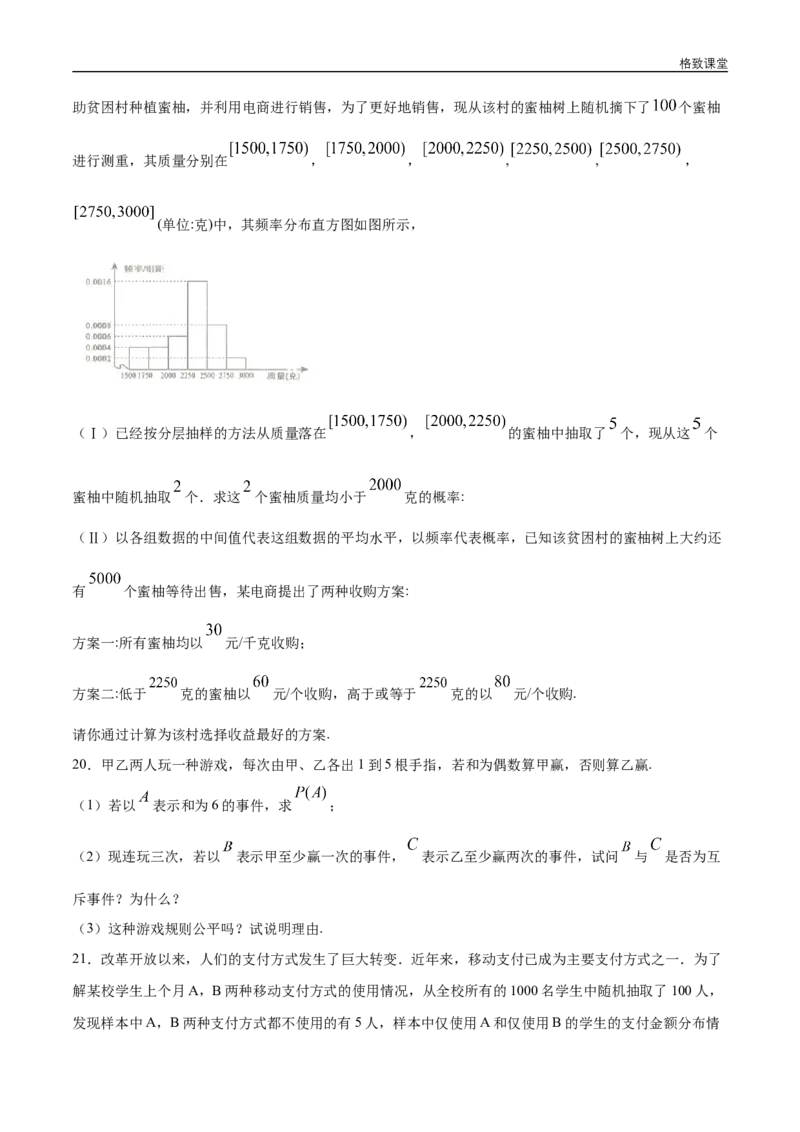
8.如图所示的电路中,5只箱子表示保险匣,设5个盒子分别被断开为事件A,B,C,D,E.箱中所示数值表示通电
时保险丝被切断的概率,下列结错误的是( )
A.A,B两个盒子串联后畅通的概率为 B.D,E两个盒子并联后畅通的概率为
C.A,B,C三个盒子混联后畅通的概率为 D.当开关合上时,整个电路畅通的概率为
二、多选题
9.下列命题是假命题的是( )
A.对立事件一定是互斥事件
B.若A,B为两个随机事件,则P(A∪B)=P(A)+P(B)
C.若事件A,B,C彼此互斥,则P(A)+P(B)+P(C)=1;
D.若事件A,B满足P(A)+P(B)=1,则A与B是对立事件.
10.下列各对事件中,M,N是相互独立事件的有( )
A.掷1枚质地均匀的骰子一次,事件 “出现的点数为奇数”,事件 “出现的点数为偶数”格致课堂
B.袋中有5个白球,5个黄球,除颜色外完全相同,依次不放回地摸两次,事件 “第1次摸到红球”,事件
“第2次模到红球”
C.分别抛掷2枚相同的硬币,事件 “第1枚为正面”,事件 “两枚结果相同”
D.一枚硬币掷两次,事件 “第一次为正面”,事件 “第二次为反面”
11.某超市随机选取1000位顾客,记录了他们购买甲、乙、丙、丁四种商品的情况,整理成如下统计表,其中
“√”表示购买,“×”表示未购买.
顾客人数 商品 甲 乙 丙 丁
100 √ × √ √
217 × √ × √
200 √ √ √ ×
300 √ × √ ×
85 √ × × ×
98 × √ × ×
根据表中数据,下列结论正确的是( )
A.顾客购买乙商品的概率最大 B.顾客同时购买乙和丙的概率约为0.2
C.顾客在甲、乙、丙、丁中同时购买3种商品的概率约为0.3 D.顾客仅购买1种商品的概率不大于0.3
12.甲罐中有3个红球、2个白球,乙罐中有4个红球、1个白球,先从甲罐中随机取出1个球放入乙罐,
分别以 , 表示由甲罐中取出的球是红球、白球的事件,再从乙罐中随机取出1个球,以B表示从乙罐
中取出的球是红球的事件,下列命题正确的是( )
A. B.事件B与事件 相互独立
C.事件B与事件 相互独立 D. , 互斥
三、填空题
13.玲玲和倩倩下象棋,为了确定谁先走第一步,玲玲对倩倩说:“拿一个飞镖射向如图所示的靶中,若射中区
域所标的数字大于3,则我先走第一步,否则你先走第一步.”你认为这个游戏规则公平吗?_____.(填“公平”或格致课堂
“不公平”)
14.在抛掷一颗骰子的试验中,事件 表示“不大于4的偶数点出现”,事件 表示“小于5的点数出
现”,则事件 发生的概率为________( 表示 的对立事件).
15.一个口袋内装有大小相同的红球、白球和黑球,从中摸出一个球,摸出红球或白球的概率为0.58,摸
出红球或黑球的概率为0.62,那么摸出红球的概率为________.
16.某地移动分公司为打破“流量月清零”的做法,推出流量“季度包”“半年包”“一年以上”三种业
务.甲乙丙分别随机选择其中一种流量业务,则至少有一人选择“半年包”业务的概率是__________.
四、解答题
17.现有7名数理化成绩优秀者,分别用 , , , , , , 表示,其中 , , 的数学成绩优秀, ,
的物理成绩优秀, , 的化学成绩优秀.从中选出数学、物理、化学成绩优秀者各1名,组成一个小组代表
学校参加竞赛,求 和 不全被选中的概率.
18.在一个选拔项目中,每个选手都需要进行4轮考核,每轮设有一个问题,能正确回答者进入下一轮考
核,否则被淘汰.已知某选手能正确回答第一、二、三、四轮问题的概率分别为 、 、 、 ,且各轮
问题能否正确回答互不影响.
(Ⅰ)求该选手进入第三轮才被淘汰的概率;
(Ⅱ)求该选手至多进入第三轮考核的概率;
19.十九大提出,坚决打赢脱贫攻坚战,某帮扶单位为帮助定点扶贫村真脱贫,坚持扶贫同扶智相结合,帮格致课堂
助贫困村种植蜜柚,并利用电商进行销售,为了更好地销售,现从该村的蜜柚树上随机摘下了 个蜜柚
进行测重,其质量分别在 , , , , ,
(单位:克)中,其频率分布直方图如图所示,
(Ⅰ)已经按分层抽样的方法从质量落在 , 的蜜柚中抽取了 个,现从这 个
蜜柚中随机抽取 个.求这 个蜜柚质量均小于 克的概率:
(Ⅱ)以各组数据的中间值代表这组数据的平均水平,以频率代表概率,已知该贫困村的蜜柚树上大约还
有 个蜜柚等待出售,某电商提出了两种收购方案:
方案一:所有蜜柚均以 元/千克收购;
方案二:低于 克的蜜柚以 元/个收购,高于或等于 克的以 元/个收购.
请你通过计算为该村选择收益最好的方案.
20.甲乙两人玩一种游戏,每次由甲、乙各出1到5根手指,若和为偶数算甲赢,否则算乙赢.
(1)若以 表示和为6的事件,求 ;
(2)现连玩三次,若以 表示甲至少赢一次的事件, 表示乙至少赢两次的事件,试问 与 是否为互
斥事件?为什么?
(3)这种游戏规则公平吗?试说明理由.
21.改革开放以来,人们的支付方式发生了巨大转变.近年来,移动支付已成为主要支付方式之一.为了
解某校学生上个月A,B两种移动支付方式的使用情况,从全校所有的1000名学生中随机抽取了100人,
发现样本中A,B两种支付方式都不使用的有5人,样本中仅使用A和仅使用B的学生的支付金额分布情格致课堂
况如下:
支
大于2000元
不大于2000元
付金额
支付方式
仅使用A 27人 3人
仅使用B 24人 1人
(Ⅰ)估计该校学生中上个月A,B两种支付方式都使用的人数;
(Ⅱ)从样本仅使用B的学生中随机抽取1人,求该学生上个月支付金额大于2000元的概率;
(Ⅲ)已知上个月样本学生的支付方式在本月没有变化.现从样本仅使用B的学生中随机抽查1人,发现
他本月的支付金额大于2000元.结合(Ⅱ)的结果,能否认为样本仅使用B的学生中本月支付金额大于
2000元的人数有变化?说明理由.
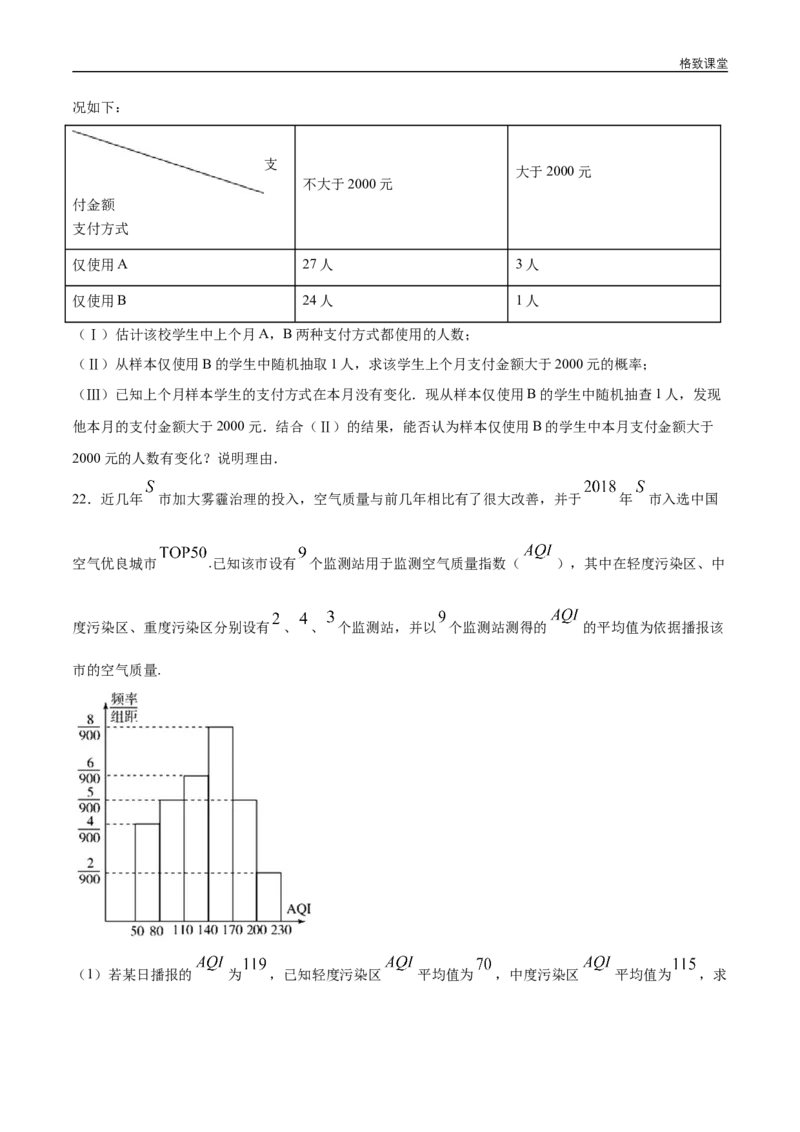
22.近几年 市加大雾霾治理的投入,空气质量与前几年相比有了很大改善,并于 年 市入选中国
空气优良城市 .已知该市设有 个监测站用于监测空气质量指数( ),其中在轻度污染区、中
度污染区、重度污染区分别设有 、 、 个监测站,并以 个监测站测得的 的平均值为依据播报该
市的空气质量.
(1)若某日播报的 为 ,已知轻度污染区 平均值为 ,中度污染区 平均值为 ,求格致课堂
重度污染区 平均值;
(2)如图是 年 月份 天的 的频率分布直方图, 月份仅有 天 在 内.
①某校参照官方公布的 ,如果周日 小于 就组织学生参加户外活动,以统计数据中的频率为
概率,求该校学生周日能参加户外活动的概率;
②环卫部门从 月份 不小于 的数据中抽取两天的数据进行研究,求抽取的这两天中 值在
的天数的概率.