文档内容
期末模拟卷4
一.选择题(共8小题)
1.在一次抛硬币的试验中,同学甲用一枚质地均匀的硬币做了 100次试验,发现正面朝上
出现了45次,那么出现正面朝上的频率和概率分别为( )
A.0.45 0.45 B.0.5 0.5 C.0.5 0.45 D.0.45 0.5
【分析】出现正面的频率是45÷100=0.45,出现正面的概率是0.5.
【解答】解:出现正面的频率是45÷100=0.45,出现正面的概率是0.5,
故选:D.
2.已知i是虚数单位,则复数 的实部和虚部分别是( )
A.﹣7,3 B.7,﹣3i C.7,﹣3 D.﹣7,3i
【分析】直接利用复数代数形式的乘除运算化简得答案.
【解答】解:∵z= ,
∴复数 的实部和虚部分别是7,﹣3.
故选:C.
3.在某次测量中得到的A样本数据如下:42,43,46,52,42,50,若B样本数据恰好是
A样本数据每个都减5后所得数据,则A、B两样本的下列数字特征对应相同的是(
)
A.平均数 B.标准差 C.众数 D.中位数
【分析】根据样本A,B中数据之间的关系,结合众数,平均数,中位数和标准差的定
义即可得到结论.
【解答】解:设样本A中的数据为x,则样本B中的数据为y=x﹣5,
i i i
则样本数据B中的众数和平均数以及中位数和A中的众数,平均数,中位数相差5,
只有标准差没有发生变化,
故选:B.
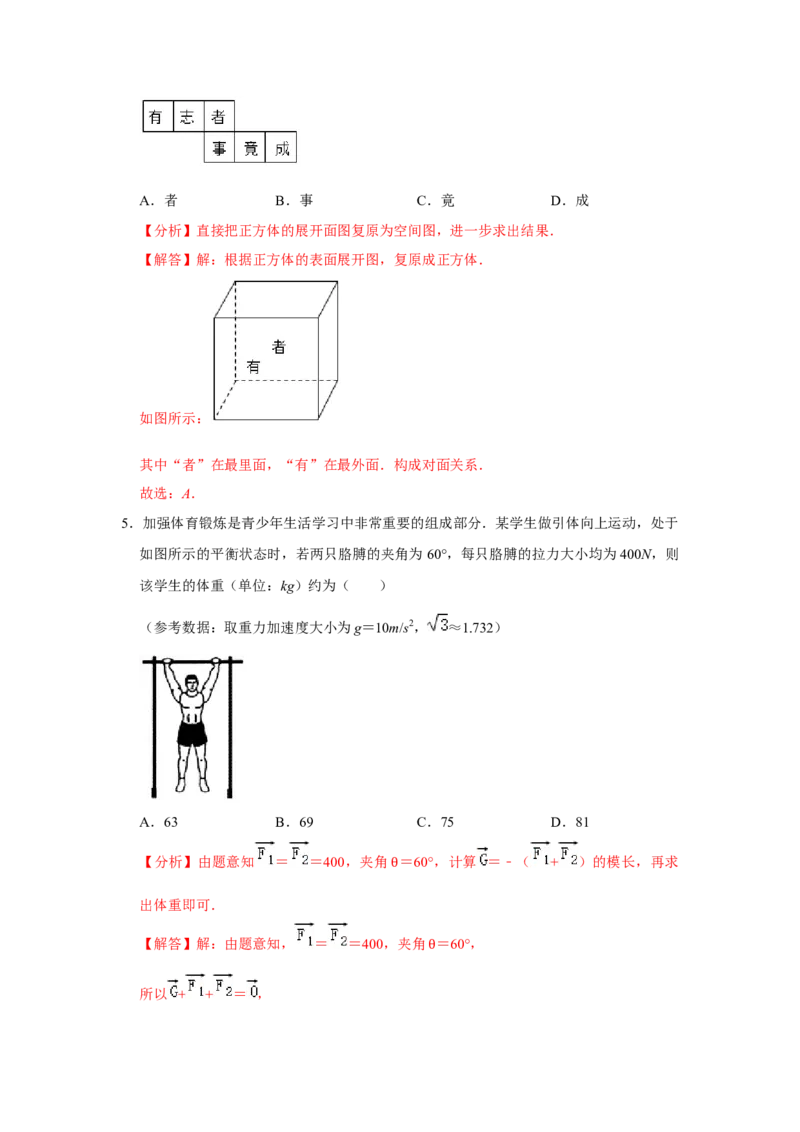
4.如图是一个正方体的表面展开图,则图中“有”在正方体中所在的面的对面上的是(
)A.者 B.事 C.竟 D.成
【分析】直接把正方体的展开面图复原为空间图,进一步求出结果.
【解答】解:根据正方体的表面展开图,复原成正方体.
如图所示:
其中“者”在最里面,“有”在最外面.构成对面关系.
故选:A.
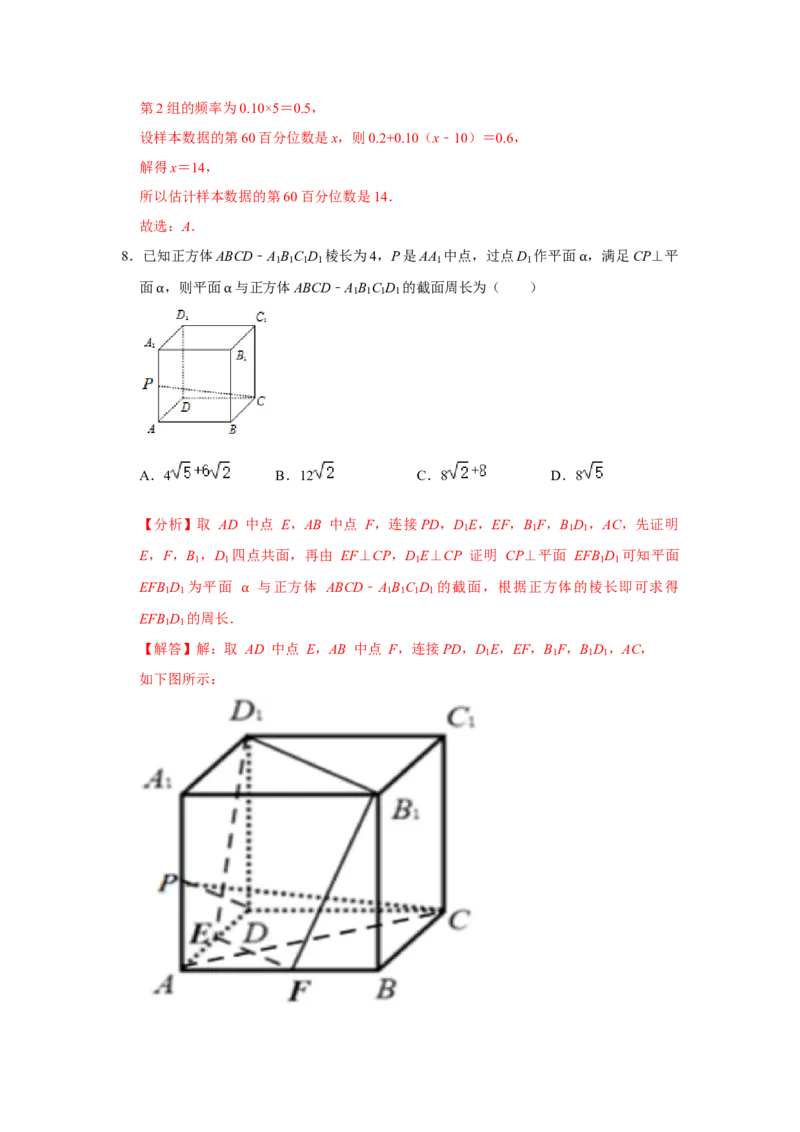
5.加强体育锻炼是青少年生活学习中非常重要的组成部分.某学生做引体向上运动,处于
如图所示的平衡状态时,若两只胳膊的夹角为 60°,每只胳膊的拉力大小均为400N,则
该学生的体重(单位:kg)约为( )
(参考数据:取重力加速度大小为g=10m/s2, ≈1.732)
A.63 B.69 C.75 D.81
【分析】由题意知 = =400,夹角 =60°,计算 =﹣( + )的模长,再求
θ
出体重即可.
【解答】解:由题意知, = =400,夹角 =60°,
θ
所以 + + = ,即 =﹣( + );
所以 = =4002+2×400×400×cos60°+4002=3×4002;
| |=400 (N),
则该学生的体重(单位:kg)约为40 =40×1.732≈69(kg),
故选:B.
6.已知向量 不共线, , ,若 ,则m=( )
A.﹣12 B.﹣9 C.﹣6 D.﹣3
【分析】由向量平行的性质得3 + = m + (m+2) ,由此能求出m.
λ λ
【解答】解:∵向量 不共线, , , ,
∴3 + = m + (m+2) ,
λ λ
∴ ,
解得 =﹣1,m=﹣3.
故选:λ D.
7.如图所示是一样本的频率分布直方图,样本数据共分 3组,分别为[5,10),[10,
15),[15,20].估计样本数据的第60百分位数是( )
A.14 B.15 C.16 D.17
【分析】由频率分布直方图,根据样本数据的百分位数列方程求出即可.
【解答】解:由频率分布直方图知,第1组的频率为0.04×5=0.2,第2组的频率为0.10×5=0.5,
设样本数据的第60百分位数是x,则0.2+0.10(x﹣10)=0.6,
解得x=14,
所以估计样本数据的第60百分位数是14.
故选:A.
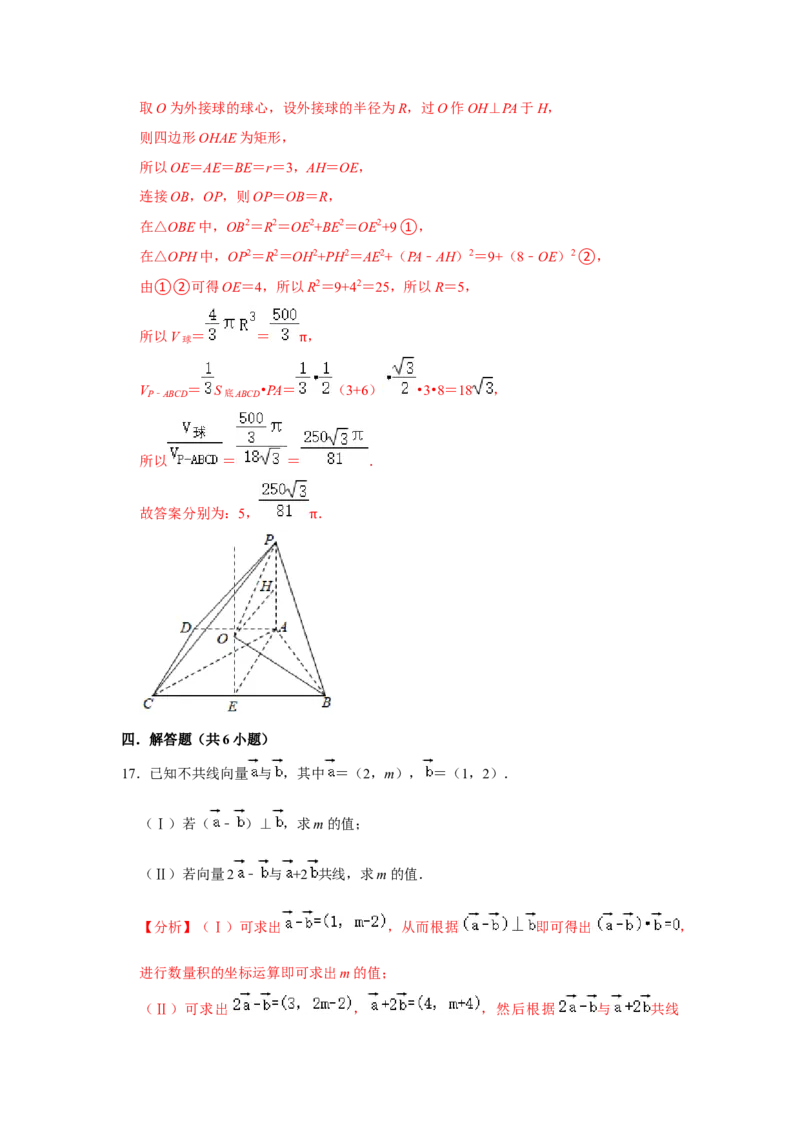
8.已知正方体ABCD﹣A B C D 棱长为4,P是AA 中点,过点D 作平面 ,满足CP⊥平
1 1 1 1 1 1
面 ,则平面 与正方体ABCD﹣A B C D 的截面周长为( ) α
1 1 1 1
α α
A.4 B.12 C.8 D.8
【分析】取 AD 中点 E,AB 中点 F,连接PD,D E,EF,B F,B D ,AC,先证明
1 1 1 1
E,F,B ,D 四点共面,再由 EF⊥CP,D E⊥CP 证明 CP⊥平面 EFB D 可知平面
1 1 1 1 1
EFB D 为平面 与正方体 ABCD﹣A B C D 的截面,根据正方体的棱长即可求得
1 1 1 1 1 1
EFB D 的周长.α
1 1
【解答】解:取 AD 中点 E,AB 中点 F,连接PD,D E,EF,B F,B D ,AC,
1 1 1 1
如下图所示:E 为 AD 中点,F 为 AB 中点,则 EF∥BD,BD∥B D
1 1
所以 EF∥B D
1 1
所以 E,F,B ,D 四点共面.
1 1
根据正方形性质可知 CD⊥平面 ADD A ,
1 1
而 D E 平面ADD A ,所以 CD⊥D E,
1 1 1 1
A△D
1
D⊂E≌△DAP,可知∠ED
1
D=∠PDA,
而∠PDA+∠PDD =90°,所以∠ED D+∠PDD =90°,
1 1 1
即 PD⊥D E
1
为 CD∩PD=D,所以 D E⊥平面 PDC,
1
而CP 平面 PDC,所以 D E⊥CP;
1
E 为 ⊂AD 中点,F 为 AB 中点,由正方形和正方体性质可知
EF⊥AC,PA⊥EF,且 PA∩AC=A,
所以 EF⊥平面 PAC,而 CP 平面 PDC,
所以 EF⊥CP,又因为 D
1
E⊥⊂CP,D
1
E∩EF=E
所以 CP⊥平面 EFB D
1 1
即平面 EFB D 为平面 与正方体 ABCD﹣A B C D 的截面,
1 1 1 1 1 1
正方体 ABCD﹣A
1
B
1
C
1
Dα1 棱长为 4
所以 EFB D 的周长为 B D +D E+EF+B F
1 1 1 1 1 1
=
= ,
故选:A.
二.多选题(共4小题)
9.某城市为了解二手房成交价格的变化规律,更有效地调控房产经济,收集并整理了
2019年1月至2019年12月期间二手房成交均价(单位:元/平方米)的数据(均价=销
售总额÷销售总面积),绘制了下面的折线统计图,那么下列结论中正确的有( )A.月均价的极差大于4000元/平方米
B.年均价一定小于18000元/平方米
C.月均价高峰期大致在9月份和10月份
D.上半年月均价变化相对下半年,波动性较小,变化比较平稳
【分析】数据分析题目,可根据定义进行分析判断.
【解答】A.极差等于极大值﹣极小值.根据折线统计图,可得极大值>19000,极小值
<15000,所以极差>19000﹣15000=4000元/平方米,故A正确;
B.由于每月的成交数量未知,因此平均价无法确定,故B错误;
C.根据折线图可得,月均价高峰期大致在9月份和10月份,故C正确;
D.根据折线图,可知1﹣6月份极差<18000﹣15000=3000元/平方米,7﹣12月份极
差>4000元/平方米,所以可判定上半年月均价变化相对波动性较小,变化比较平稳.
故D正确.
故选:ACD.
10.在△ABC中,角A、B、C所对的边分别为a、b、c,下列结论正确的是( )
A.若b2+c2﹣a2>0,则△ABC为锐角三角形
B.若A>B,则sinA>sinB
C.若b=3,A=60°,三角形面积S=3 ,则a=
D.若acosA=bcosB,则△ABC为等腰三角形
【分析】A,根据余弦定理,判定命题A为锐角;
B,由大角对大边,及正弦定理判定;
C,利用三角形的面积计算公式、余弦定理即可得出;
D,据正弦定理把等式acosA=bcosB的边换成角的正弦,再利用倍角公式化简整理得
sin2A=sin2B,进而推断A=B,或A+B=90°,即可判定.
【解答】解:对于A,若b2+c2﹣a2>0,则cosA>0,A为锐角,不能判定△ABC为锐角三角形,故错;
对于B,在△ABC中,若a>b,则2RsinA>2RsinB,则sinA>sinB,故正确;
对于C,A=60°,b=3,面积S=3 ,即有 ,解得c=4.
∴a2=b2+c2﹣2bccosA=32+42﹣2×3×4cos60°=13.∴a= ,故正确;
对于D,∵acosA=bcosB,∴sinAcosA=sinBcosB,
∴sin2A=sin2B,∴A=B,或2A+2B=180°即A+B=90°,
∴△ABC为等腰或直角三角形,故不正确.
故选:BC.
11.下列说法正确的是( )
A.对于任意两个向量 ,若 |,且 与 同向,则
B.已知 , 为单位向量,若 ,则 在 上的投影向量为
C.设 为非零向量,则“存在负数 ,使得 ”是“ ”的充分不必
λ
要条件
D.若 ,则 与 的夹角是钝角
【分析】利用向量的定义判断A;向量的投影判断B;向量的数量积与充要条件判断
C;向量的数量积的符号判断D;
【解答】解:对于任意两个向量 ,若 |,且 与 同向,
但是不能说 ,因为向量不能比较大小,所以A不正确;
已知 , 为单位向量,若 ,
则 在 上的投影为: =﹣3 ,投影向量为 ,所以B正确;
存在负数 ,使得 ,则 与 反向共线,夹角为180°,此时 成立,
λ当 成立时,则 与 夹角满足90°< ≤180°,则 与 不一定反向共线,
θ
即“存在负数 ,使得 ”是“ ”的充分而不必要条件成立,故C正确,
λ
若 ,则 与 的夹角是钝角或平角,所以D不正确;
故选:BC.
12.如图,正方体 ABCD﹣A B C D 的棱长为1,动点E在线段A C 上,F、M分别是
1 1 1 1 1 1
AD、CD的中点,则下列结论中正确的是( )
A.FM∥A C
1 1
B.BM⊥平面CC F
1
C.存在点E,使得平面BEF∥平面CC D D
1 1
D.三棱锥B﹣CEF的体积为定值
【分析】本题利用中位线定理以及线面垂直,三棱锥的特征求解.
【解答】解:A:∵F,M分别是AD,CD的中点,
∴FM∥AC∥A C ,故A正确;
1 1
B:由平面几何得BM⊥CF,又BM⊥C C,
1
∴BM⊥平面CC F,故B正确;
1
C:BF与平面CC D D有交点,
1 1
∴不存在点E,使平面BEF∥平面CC D D,故C错误;
1 1
D:三棱锥B﹣CEF以面BCF为底,则高是定值,
∴三棱锥B﹣CEF的体积为定值,故D正确.
故选:ABD.
三.填空题(共4小题)
13.甲、乙两人参加“社会主义价值观”知识竞赛,甲、乙两人能荣获一等奖的概率分别为 和 ,甲、乙两人是否获得一等奖相互独立,则这两个人中恰有一人获得一等奖的
概率为 .
【分析】设事件事件A表示“甲参加知识竞赛”,事件B表示“乙参加知识竞赛”,则
P(A)= ,P(B)= ,利用相互独立事件概率乘法公式和互斥事件概率加法公式
能求出这两个人中恰有一人获得一等奖的概率.
【解答】解:设事件事件A表示“甲参加知识竞赛”,事件B表示“乙参加知识竞赛”,
则P(A)= ,P(B)= ,
∵甲、乙两人是否获得一等奖相互独立,
∴这两个人中恰有一人获得一等奖的概率为:
P(A )+P( )=P(A)P( )+P( )P(B)
=
= .
故答案为: .
14.我国古代数学名著《九章算术》有一抽样问题:“今有北乡若干人,西乡七千四百八
十八人,南乡六千九百一十二人,凡三乡,发役三百人,而北乡需遣一百零八人,问北
乡人数几何?“其意思为:“今有某地北面若干人,西面有 7488人,南面有6912人,
这三面要征调300人,而北面共征调108人(用分层抽样的方法),则北面共有 810 0
人.”
【分析】根据分层抽样时抽取的比例相等,列方程求出结果.
【解答】解:设北面有x人,根据题意得
= ,
解得x=8100.
故答案为:8100.
15.如图,为测量山高MN,选择A和另一座山的山顶C为测量观测点.从A点测得M点的仰角∠MAN=60°,C点的仰角∠CAB=45°以及∠MAC=75°;从C点测得∠MCA=
60°.已知山高BC=100m,则山高MN= 15 0 m.
【分析】由题意,可先求出AC的值,从而由正弦定理可求AM的值,在RT△MNA中,
AM=100 m,∠MAN=60°,从而可求得MN的值.
【解答】解:在RT△ABC中,∠CAB=45°,BC=100m,所以AC=100 m.
在△AMC中,∠MAC=75°,∠MCA=60°,从而∠AMC=45°,
由正弦定理得, ,因此AM=100 m.
在RT△MNA中,AM=100 m,∠MAN=60°,由
得MN=100 × =150m.
故答案为:150.
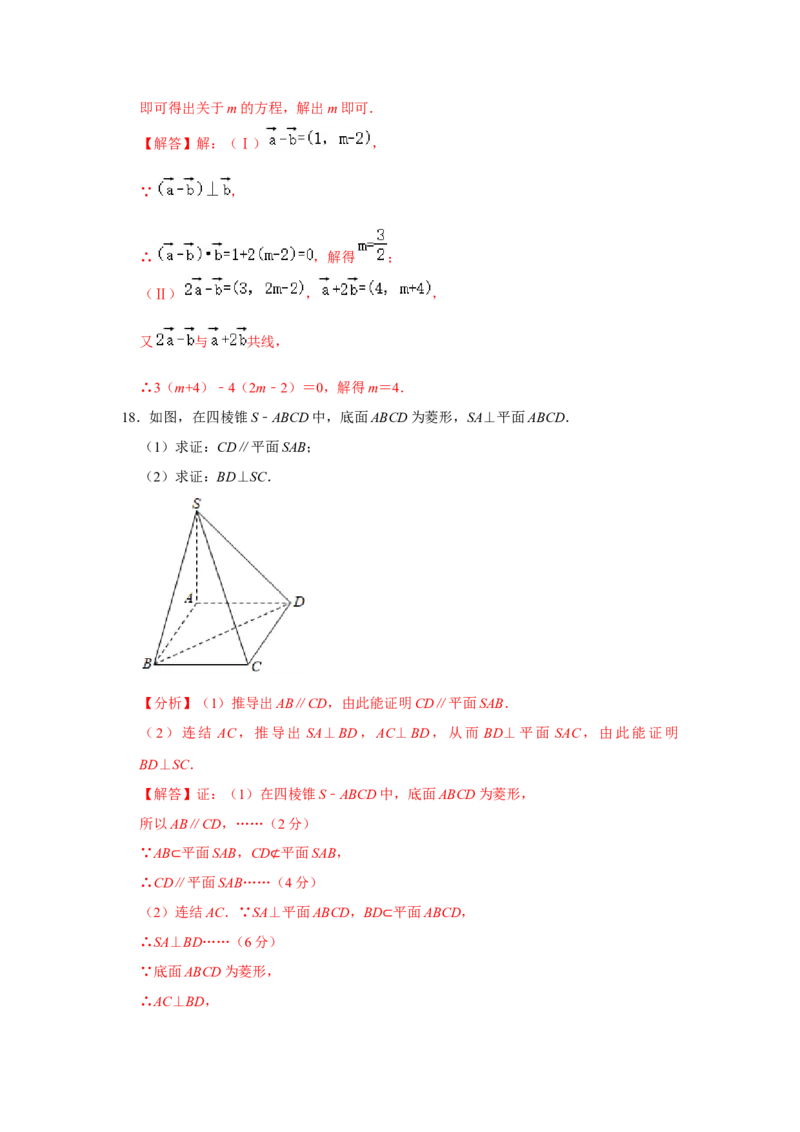
16.在底面为等腰梯形的四棱锥P﹣ABCD中,AD∥BC,AB=AD=CD=3,BC=6,PA=
8,PA⊥平面ABCD,该四棱锥的各个顶点都在球O的球面上,则球O的半径为 5 ,
球O的体积与四棱锥P﹣ABCD的体积的比值为 .
【分析】由题意可得底面等腰梯形的外接圆的半径,过底面 π 外 接圆的圆心E作垂直于底
面的直线,则外接球的球心在此直线上,在两个三角形中求出外接球的半径,进而求出
球的体积,及体积之比.
【解答】解:如图,取BC的中点E,过E作EO⊥面AC,
因为PA⊥面AC,所以PA∥OE
因为AB=CD,AD∥BC,AB=AD=CD=3,BC=6,
所以△ABC为等边三角形,∠ABC=60°∠CAB=90°,
所以E为梯形ABCD的外接圆的圆心,则外接圆的半径r=3,取O为外接球的球心,设外接球的半径为R,过O作OH⊥PA于H,
则四边形OHAE为矩形,
所以OE=AE=BE=r=3,AH=OE,
连接OB,OP,则OP=OB=R,
在△OBE中,OB2=R2=OE2+BE2=OE2+9①,
在△OPH中,OP2=R2=OH2+PH2=AE2+(PA﹣AH)2=9+(8﹣OE)2②,
由①②可得OE=4,所以R2=9+42=25,所以R=5,
所以V球 = = ,
π
V P﹣ABCD = S底ABCD •PA= (3+6) •3•8=18 ,
所以 = = .
故答案分别为:5, .
π
四.解答题(共6小题)
17.已知不共线向量 与 ,其中 =(2,m), =(1,2).
(Ⅰ)若( ﹣ )⊥ ,求m的值;
(Ⅱ)若向量2 ﹣ 与 +2 共线,求m的值.
【分析】(Ⅰ)可求出 ,从而根据 即可得出 ,
进行数量积的坐标运算即可求出m的值;
(Ⅱ)可求出 , ,然后根据 与 共线即可得出关于m的方程,解出m即可.
【解答】解:(Ⅰ) ,
∵ ,
∴ ,解得 ;
(Ⅱ) , ,
又 与 共线,
∴3(m+4)﹣4(2m﹣2)=0,解得m=4.
18.如图,在四棱锥S﹣ABCD中,底面ABCD为菱形,SA⊥平面ABCD.
(1)求证:CD∥平面SAB;
(2)求证:BD⊥SC.
【分析】(1)推导出AB∥CD,由此能证明CD∥平面SAB.
(2)连结 AC,推导出 SA⊥BD,AC⊥BD,从而 BD⊥平面 SAC,由此能证明
BD⊥SC.
【解答】证:(1)在四棱锥S﹣ABCD中,底面ABCD为菱形,
所以AB∥CD,……(2分)
∵AB 平面SAB,CD 平面SAB,
∴CD⊂∥平面SAB……⊄(4分)
(2)连结AC.∵SA⊥平面ABCD,BD 平面ABCD,
∴SA⊥BD……(6分) ⊂
∵底面ABCD为菱形,
∴AC⊥BD,∵AC∩SA=A,AC,SA 平面SAC,
∴BD⊥平面SAC,又SC⊂ 平面SAC……(9分)
∴BD⊥SC.……(10分⊂)
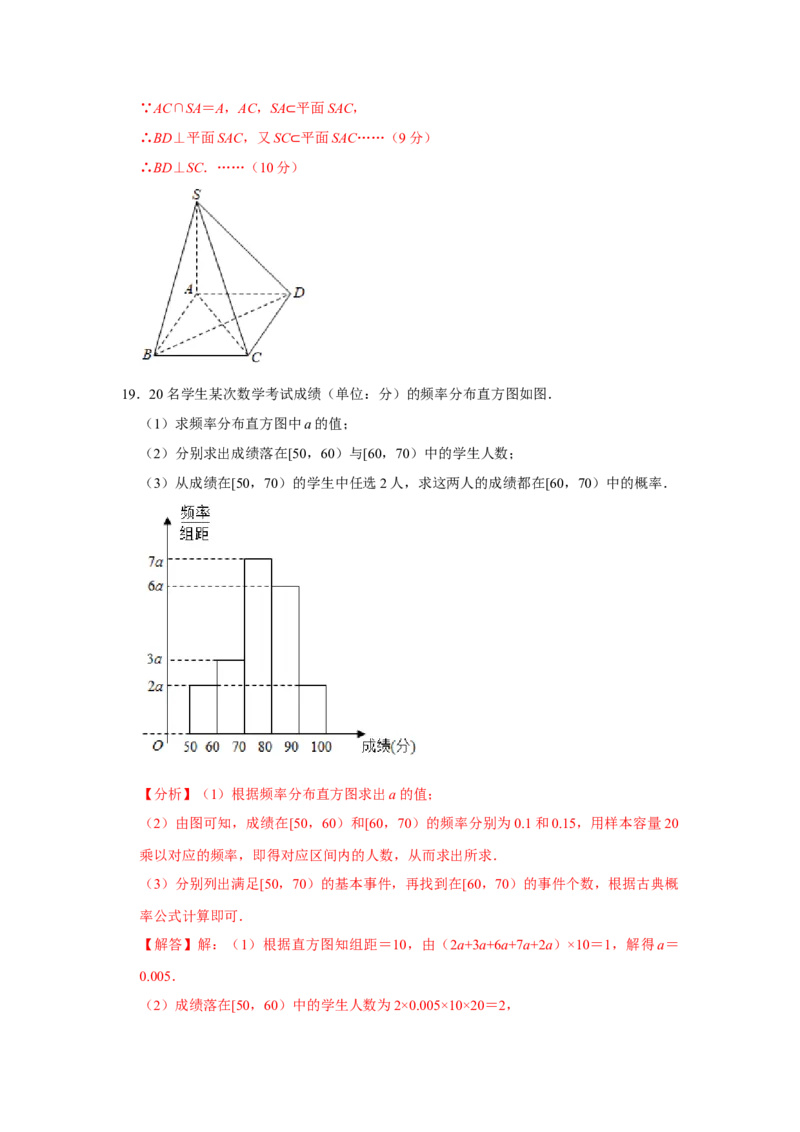
19.20名学生某次数学考试成绩(单位:分)的频率分布直方图如图.
(1)求频率分布直方图中a的值;
(2)分别求出成绩落在[50,60)与[60,70)中的学生人数;
(3)从成绩在[50,70)的学生中任选2人,求这两人的成绩都在[60,70)中的概率.
【分析】(1)根据频率分布直方图求出a的值;
(2)由图可知,成绩在[50,60)和[60,70)的频率分别为0.1和0.15,用样本容量20
乘以对应的频率,即得对应区间内的人数,从而求出所求.
(3)分别列出满足[50,70)的基本事件,再找到在[60,70)的事件个数,根据古典概
率公式计算即可.
【解答】解:(1)根据直方图知组距=10,由(2a+3a+6a+7a+2a)×10=1,解得a=
0.005.
(2)成绩落在[50,60)中的学生人数为2×0.005×10×20=2,成绩落在[60,70)中的学生人数为3×0.005×10×20=3.
(3)记成绩落在[50,60)中的2人为A,B,成绩落在[60,70)中的3人为C,D,
E,
则成绩在[50,70)的学生任选2人的基本事件有AB,AC,AD,AE,BC,BD,BE,
CD,CE,DE共10个,
其中2人的成绩都在[60,70)中的基本事件有CD,CE,DE共3个,
故所求概率为P= .
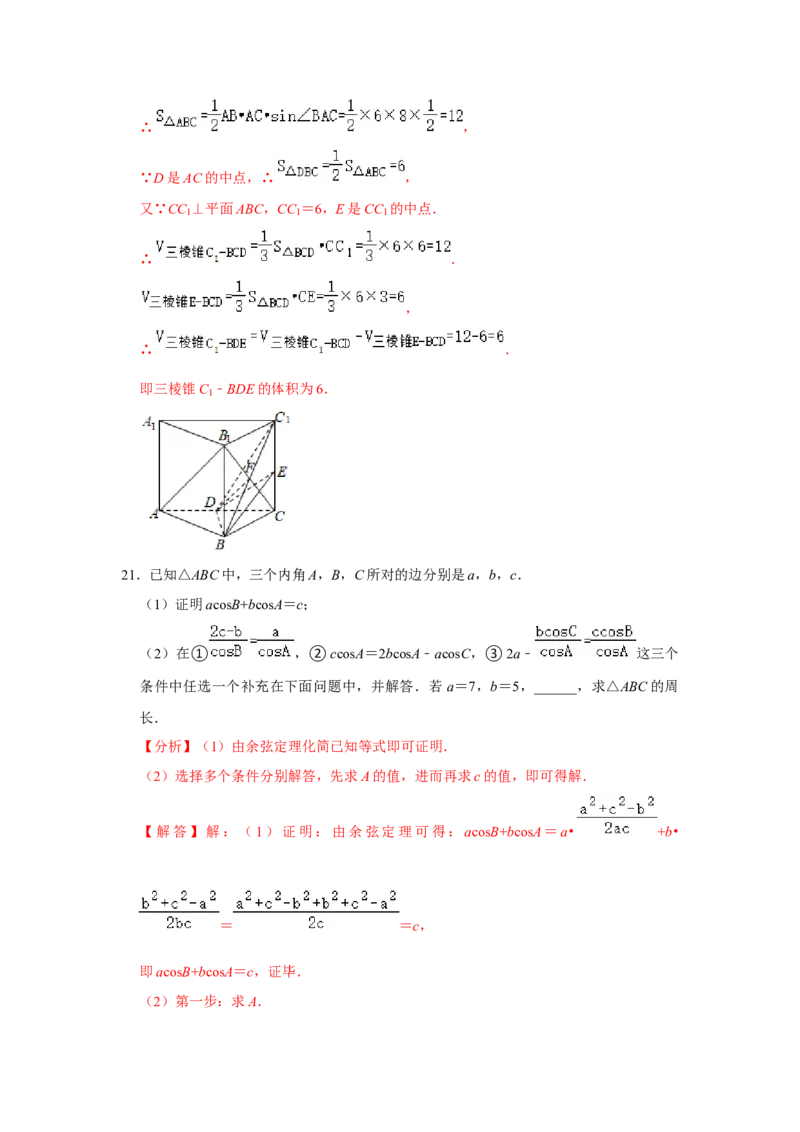
20.如图,在三棱柱ABC﹣A B C 中,AA ⊥平面ABC,AB=AA =6,AC=8,D,E分别
1 1 1 1 1
是AC,CC 的中点.
1
(1)求证:AB ∥平面BDC ;
1 1
(2)若异面直线AB与A C 所成的角为30°,求三棱锥C ﹣BDE的体积.
1 1 1
【分析】(1)如图,连接B C,交BC 于点F,连接DF,由已知结合三角形中位线定
1 1
理可得DF∥AB ,再由直线与平面平行的判定定理,证明AB ∥平面BDC ;
1 1 1
(2)由AC∥A C ,可得∠BAC即为异面直线AB与A C 所成的角为30°,求三角形
1 1 1 1
ABC的面积,得到三角形DBC的面积,然后分别求出三棱锥C ﹣BCD,E﹣BCD的体
1
积,再由 求解.
【解答】解:(1)证明:如图,连接B C,交BC 于点F,连接DF,
1 1
在△ACB 中,由于D为AC的中点,F为B C的中点
1 1
∴DF为△ACB 的中位线,∴DF∥AB ,
1 1
∵DF 平面BDC ,AB 平面BDC ,
1 1 1
∴AB 1⊂∥平面BDC 1 ; ⊄
(2)∵AC∥A C ,∴∠BAC即为异面直线AB与A C 所成的角,
1 1 1 1
∵异面直线AB与A C 所成的角为30°,∴∠BAC=30°,
1 1∴ ,
∵D是AC的中点,∴ ,
又∵CC ⊥平面ABC,CC =6,E是CC 的中点.
1 1 1
∴ .
,
∴ .
即三棱锥C ﹣BDE的体积为6.
1
21.已知△ABC中,三个内角A,B,C所对的边分别是a,b,c.
(1)证明acosB+bcosA=c;
(2)在① ,②ccosA=2bcosA﹣acosC,③2a﹣ 这三个
条件中任选一个补充在下面问题中,并解答.若 a=7,b=5,______,求△ABC的周
长.
【分析】(1)由余弦定理化简已知等式即可证明.
(2)选择多个条件分别解答,先求A的值,进而再求c的值,即可得解.
【解答】解:(1)证明:由余弦定理可得:acosB+bcosA=a• +b•
= =c,
即acosB+bcosA=c,证毕.
(2)第一步:求A.选①:
∵ ,
∴2ccosA=bcosA+acosB,
∴由(1)中所证结论可得:2ccosA=c,可得cosA= ,
∵A (0, ),
∈ π
∴A= .
选②:
∵ccosA=2bcosA﹣acosC,
∴2bcosA=acosC+ccosA,
由(1)中的证明同理可得:acosC+ccosA=b,
∴2bcoA=b,可得cosA= ,
∵A (0, ),
∈ π
∴A= .
选③:
∵2a﹣ ,
∴2acosA=bcosC+ccosB,
由(1)中的证明过程同理可得bcosC+ccosB=a,
∴2acoA=a,可得cosA= ,
∵A (0, ),
∈ π
∴A= .
第二步:求c
在△ABC中,由余弦定理可得:a2=b2+c2﹣2bccosA=25+c2﹣10c =49,即c2﹣5c﹣
24=0,解得c=8,或c=﹣3(舍去),
所以a+b+c=7+5+8=20,即△ABC的周长为20.
22.2019年,我国施行个人所得税专项附加扣除办法,涉及子女教育、继续教育、大病医疗、住房贷款利息或者住房租金、赡养老人等六项专项附加扣除.某单位老、中、青员
工分别有72,108,120人,现采用分层抽样的方法,从该单位上述员工中抽取 25人调
查专项附加扣除的享受情况.
员工 A B C D E F
项目
子女教育 〇 〇 × 〇 × 〇
继续教育 × × 〇 × 〇 〇
大病医疗 × × × 〇 × ×
住房贷款利息 〇 〇 × × 〇 〇
住房租金 × × 〇 × × ×
赡养老人 〇 〇 × × × 〇
(1)应从老、中、青员工中分别抽取多少人?
(2)抽取的25人中,享受至少两项专项附加扣除的员工有6人,分别记为A,B,C,
D,E,F.享受情况如上表,其中“〇”表示享受,“×”表示不享受现从这6人中随
机抽取2人接受采访.
(i)试用所给字母列举出所有可能的抽取结果;
(ii)设M为事件“抽取的2人享受的专项附加扣除至少有一项相同”,求事件 M发生
的概率.
【分析】(1)老、中、青员工人数之比为6:9:10,利用分层抽样的性质能求出应从
老、中、青员工中分别抽取多少人.
(2)(i)从已知的6人中随机抽取2人,利用列举法能求出所有可能结果.
(ii)由表格知,列举出符合题意的所有可能结果,由此能求出事件M发生的概率.
【解答】解:(1)由已知,老、中、青员工人数之比为6:9:10,
由于采用分层抽样的方法从中抽取25位员工,
因此应从老、中、青员工中分别抽取6人,9人,10人.
(2)(i)从已知的6人中随机抽取2人的所有可能结果为:
{A,B},{A,C},{A,D},{A,E},{A,F},{B,C},{B,D},{B,E},
{B,F},{C,D},{C,E},{C,F},{D,E},{D,F},{E,F}共15种.
(ii)由表格知,符合题意的所有可能结果为:
{A,B},{A,D},{A,E},{A,F},{B,D},{B,E},{B,F},
{C,E},{C,F},{D,F},{E,F}共11种.所以,事件M发生的概率 .