文档内容
2024 年深圳市普通高中高一年级调研考试
数 学
本试卷共 4 页, 19 小题, 满分 150 分。考试用时 120 分钟。
注意事项:
1. 答题前, 考生请务必用黑色字迹钢笔或签字笔将自己的姓名、准考证号填写在答题卡上。
用 2B 铅笔将试卷类型 (A) 填涂在答题卡相应位置上。将条形码横贴在答题卡右上角
“条形码粘贴处”。
2. 作答选择题时, 选出每小题答案后, 用 2B 铅笔把答题卡上对应题目选项的答案信息点
涂黑; 如需改动, 用橡皮擦干净后, 再选涂其他答案, 答案不能答在试卷上。
3. 非选择题必须用黑色字迹钢笔或签字笔作答, 答案必须写在答题卡各题目指定区域内相
应位置上; 如需改动, 先划掉原来的答案, 然后再写上新的答案; 不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
4. 考生必须保持答题卡的整洁。考试结束后, 将试卷和答题卡一并交回。
一、选择题: 本题共 8 小题, 每小题 5 分, 共 40 分。在每小题给出的四个选项中, 只
有一项是符合题目要求的。
1.已知集合 A={−1,1,3},B={0,1,3},则 A∪B=( )
A.{1,3} B.{−1,1,3} C.{0,1,3} D.
{−1,0,1,3}
2.函数 f (x)=lnx+x−2 的零点所在的区间为( )
A.(0,1) B.(1,2) C.(2,3) D.(3,4)
3.已知幂函数 ,则 “ ” 是“ 在 上单调递增”的(
f (x)=xα α>0 f (x) (0,+∞)
)
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
4.已知向量 ,则 ( )
⃗a=(2,0),⃗b=(1,2),(λ⃗a+⃗b)⊥⃗a λ=
1
A.-1 B.− C.1 D.2
2
5.设 m,n 是两条不同的直线, α,β 是两个不同的平面,下列命题中为真命题的是
( )
试卷第1页,共4页
学科网(北京)股份有限公司A.若 m//α,n⊂α ,则 m//n B.若 m//α,α//β ,则
m//β
C.若 m⊥α,m⊥n ,则 n//α D.若 m⊥α,m//β ,则
α⊥β
6.已知 △ABC 中, ⃗AE=2⃗AB,⃗BM=2⃗MC,若 ⃗AF=x⃗AC,且 E,M,F 三点
共线, 则 x=( )
2 3 4 5
A. B. C. D.
3 4 5 6
7.已知正实数 a,b 满足 a+4b=ab,则 a+b 的最小值为( )
A.4 B.9 C.10 D.20
8.已知函数 ,则 的大
f (x)=x−sinx,a=f (π),b=f (2),c=−f (−√3) a,b,c
小关系为( )
A.a>b>c B.a>c>b C.b>c>a D.b>a>c
二、选择题: 本题共 3 小题, 每小题 6 分, 共 18 分。在每小题给出的选项中, 有多项
符合题目要求。全部选对的得 6 分, 部分选对的得部分分, 有选错的得 0 分。
9.若复数 z 满足 iz=1−i,下列说法正确的是( )
A.z 的虚部为 −i B.´z=−1+i
C.|z|=√2 D.z⋅´z=z2
10.抛掷一枚质地均匀的骰子两次,记下每次朝上的点数,设事件 A= “第一次的点数
不大于 3 ”, B= “第二次的点数不小于 4 ”, C= “两次的点数之和为 3 的倍
数”,则下列结论正确的是( )
1
A.事件 A 发生的概率 P(A)= B.事件 A 与事件 B 相互独立
2
1
C.事件 C 发生的概率 P(C)= D.事件 AB 与事件 C 对立
3
11.已知正方体 ABCD−A B C D 的棱长为 2,E 是正方形 ABB A 的中心,
1 1 1 1 1 1
F 是棱 CD (包含顶点) 上的动点, 则以下结论正确的是( )
A.EF 的最小值为 √5
B.不存在点 F,使 EF 与 A D 所成角等于 30∘
1 1
试卷第2页,共4页C.二面角 正切值的取值范围为
E−AF−B [1,√2]
25
D.当 F 为 CD 中点时,三棱锥 F−ABE 的外接球表面积为 π
4
三、填空题: 本题共 3 小题, 每小题 5 分, 共 15 分。
12.已知 1 则 ( π)
sinα= , cos α+ =
3 2
13.若 [1 ],不等式 恒成立,则 的取值范围为
∀x∈ ,2 x2−ax+1≤0 a
2
.
π
14.已知圆 O 为 △ABC 的外接圆, A= ,BC=√3,则 AO⋅(AB+AC) 的最大
3
值为 .
四 解答题: 本题共 9 小题,共 77 分、解答应笃出文学说明、证明过程或演算步骤。
15.(13分)
已知 △ABC 的内角 A,B,C 的对边分别为 a,b,c,csin A+√3acosC=0 .
(1)求 C ;
(2)若 a=4,△ABC 的面积为 √3,求 b 和 c .
16.(15 分)
已知函数 ( π),函数 的最小正周期为 ,且
f (x)=sin(ωx+φ) ω>0,|φ|< f (x) π
2
(π)
f =0
6
(1)求函数 f (x) 的解析式:
(2)求使 2f (x)−1≥0 成立的 x 的取值范围.
试卷第3页,共4页
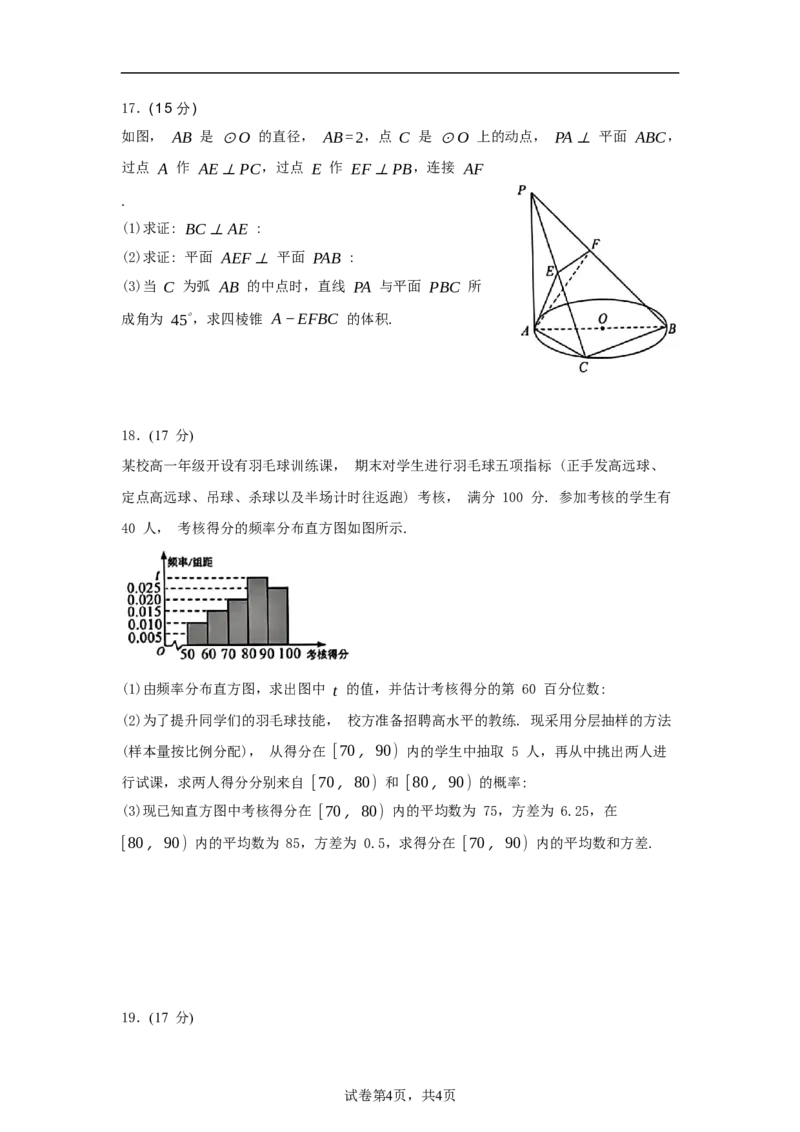
学科网(北京)股份有限公司17.(15 分)
如图, AB 是 ⊙O 的直径, AB=2,点 C 是 ⊙O 上的动点, PA⊥ 平面 ABC,
过点 A 作 AE⊥PC,过点 E 作 EF⊥PB,连接 AF
.
(1)求证: BC⊥AE :
(2)求证: 平面 AEF⊥ 平面 PAB :
(3)当 C 为弧 AB 的中点时,直线 PA 与平面 PBC 所
成角为 45∘,求四棱锥 A−EFBC 的体积.
18.(17 分)
某校高一年级开设有羽毛球训练课, 期末对学生进行羽毛球五项指标 (正手发高远球、
定点高远球、吊球、杀球以及半场计时往返跑) 考核, 满分 100 分. 参加考核的学生有
40 人, 考核得分的频率分布直方图如图所示.
(1)由频率分布直方图,求出图中 t 的值,并估计考核得分的第 60 百分位数:
(2)为了提升同学们的羽毛球技能, 校方准备招聘高水平的教练. 现采用分层抽样的方法
(样本量按比例分配), 从得分在 [70,90) 内的学生中抽取 5 人,再从中挑出两人进
行试课,求两人得分分别来自 [70,80) 和 [80,90) 的概率:
(3)现已知直方图中考核得分在 [70,80) 内的平均数为 75,方差为 6.25,在
[80,90) 内的平均数为 85,方差为 0.5,求得分在 [70,90) 内的平均数和方差.
19.(17 分)
试卷第4页,共4页已知函数 为 上的奇函数. 当 时, ( 为
y=f (x) R 0≤x≤1 f (x)=ax2+3x+c a,c
常数), f (1)=1 .
1 1
(1)当 − ≤x≤ 时,求函数 y=2f(x) 的值域:
2 2
(2)若函数 y=f (x) 的图像关于点 (1,1) 中心对称.
① 设函数 g(x)=f (x)−x,x∈R,求证: 函数 g(x) 为周期函数;
9 41
②若 − ≤f (x)≤ 对任意 x∈[m,n] 恒成立,求 n−m 的最大值.
8 8
试卷第5页,共4页
学科网(北京)股份有限公司