文档内容
2024年深圳市普通高中高一年级调研考试数学
参考答案及评分标准
1.解析:AUB={−1,0,1,3}, 选D
2..解 析 : f (1)=−1<0,f (2)=ln2>0 , 故 选 B
3.解析:充分必要件选 C
4. 【详解】∵⃗a=(2,0),⃗b=(1,2),(λ⃗a+⃗b)⊥⃗a
∴(λ⃗a+⃗b)⋅⃗a=0,即, [λ(2,0)+(1,2)]⋅(2,0)=0,
1
得:(2λ+1,2)⋅(2,0)=0,整理得,2(2λ+1)=0,λ=− ,
2
故选:B.
5.【详解】如图所示
对于A选项,A D //面ABCD,A B //面
1 1 1 1
ABCD,
但是A D 和A B 并不平行,所以选项A错误;
1 1 1 1
对于B选项,A D //面ABCD,
1 1
面ABCD//A B C D 面,
1 1 1 1
但是A D ⊂面A B C D A D 和面A B C D 并
1 1 1 1 1 1 1 1 1 1 1 1
不平行,
所以选项B错误;
对于C选项,BB ⊥面ABCD,BB ⊥BC,但是
1 1
BC⊂面ABCD,所以选项C错误
对于选项D是面面垂直的一种判定方法,所以选项D正确.故选:D
6.【详解】⃗AE=2⃗AB,⃗BM=2⃗MC,若 ⃗AF=x⃗AC,
1 2 1 2
∴⃑AM= ⃑AB+ ⃑AC= ⃑AE+ ⃑AF,
A
3 3 6 3x
又E,M,F三点共线,
1 2
∴ + =1, F
6 3x
B
即x=5, 故选:C C
M
7.【详解】因为正实数a,b满足a+4b=ab,
1 4
所以 + =1,
b a E
因此
(1 4) a 4b √a 4b
a+b=(a+b) + = +4+1+ ≥5+2 ⋅ =9,
b a b a b a
a 4b
当且仅当 = ,即¿时,等号成立;故选:B
b a
8.【详解】f(x)=x﹣sinx为奇函数, =
−f (−√3) f (√3)
当x≥0时,f(x)=x﹣sinx,f'(x)=1﹣cosx≥0,
1
学科网(北京)股份有限公司∴f(x)在(0,+∞)上单调递增,
∵π>2>√3
∴ a>b>c,故选A.
9.【详解】由iz=1−i两边乘以−i得,z=−1−i,
z的虚部为−1,z=−1+i,|z|=√(−1) 2+12=√2,
故选:BC
10. 【详解】抛掷一枚质地均匀的骰子(六个面上的数字是1、2、3、4、5、6),抛掷
两次,设第一次、第二次抛掷骰子正面朝上的点数分别为m、n,
以(m,n)为一个基本事件,则基本事件的总数为62=36,
事件A包含的基本事件有:(1,1)、(1,2)、(1,3)、(1,4)、(1,5)、(1,6)、(2,1)、(2,2)、(2,3)、
(2,4)、(2,5)、(2,6),(3,1)、(3,2)、(3,3)、(3,4)、(3,5)、(3,6),共18种,
事件B包含的基本事件有:(1,4)、(2,4)、(3,4),(4,4)、(5,4)、(6,4),(1,5)、(2,5)、
(3,5),(4,5)、(5,5)、(6,5),(1,6)、(2,6)、(3,6),(4,6)、(5,6)、(6,6),共18种,,
事件C包含的基本事件有:(1,2)、(1,5)、(2,2),(2,4)、(3,3)、(3,6)、(4,2)、(4,6)、
(5,1)、(5.4)、(6,3)、(6,6)、共12种,
事件AB包含的基本事件有:(1,4)、(1,5)、(1,6),(2,4)、(2,5)、(2,6),(3,4)、(3,5),
(3,6)、共9种,
18 1 18 1 12 9 1
P(A)= = ,P(B)= = ,P(C)= =3,,P(AB)= = ,
36 2 36 2 36 36 4
P(AB)=P(A)⋅P(B),故选:ABC.
D1 C1
11.【详解】对于A,要使EF的值最小,
即要使得E到 D H C
直线CD距离最小, F
这最小距离就是E到直线CD
的中点H距离,,为√5,
故A正确;
B1
A1
E
A G B
对于B,因为FL//A D , D1 C1
1 1
所以直线EF与A 1 D 1 所成的角, D C
即为直线EF与FL所成角, F
即∠EFL或其补角,
EL EL
tan∠EFL= =
FL 2
B1
A1
由在线段AB上存在点L,使1≤EL≤√2,
E
√3 A L B
由tan30∘= ,得B不正确
3
对于C,取AB中点M,连接EM,则EM⊥平 面A,B CD
作EN ⊥AF ,连接EN , D1 C1
所以ENM为二面角 E−AF−B的平面角。
EM 1 D C
tan∠ENM= =
F
MN MN
√2
由在线段AF上存在点N,使 ≤MN≤1
2
N
B1
A1
E
A M B
2
学科网(北京)股份有限公司D1 C1
C
D
F
O
B1
A1
E
A Z B
所以E二面角 E−AF−B 正切值的取值范围为 [1,√2],
得C正确
对D选项,如图,取AB的中点Z,
则三棱锥F−ABE的外接球的球心O在线段EN上,
设外接球O的半径为R,则OZ=2-R。
由勾股定理可得:1+(2−R) 2=R2,
5
得:R= ,
4
25
三棱锥 F−ABE 的外接球表面积为 =4πR2= π
4
故D正确.
故选:ACD.
π 1
12.【详解】因cos(α+ )=−sinα =−
2 3
1
故答案为:− .
3
[1 ]
13.【详解】解:∀x∈ ,2 ,使关于x的不等式x2−ax+1≤0恒成立,
2
1 [1 ]
则ax≥x2+1,即a≥(x+ ) ,x∈ ,2 ,
x max 2
1 [1 ] [1 ]
令g(x)=x+ ,x∈ ,2 ,则对勾函数g(x)在 ,1 上单调递减,
x 2 2
5 5
在[1,2]上单调递增所以g(x) =g(2)= ,故a∈ [ ,+∞)
max 2 2
5
故答案为:[ ,+∞).
2
1 A
14. 【 详 解 】 因 为 ⃗AO⋅⃗AB=⃗AD⋅⃗AB= ⃗AB2,
2
1
⃗AO⋅⃗AC=⃗AE⋅⃗AC= ⃗AC2, E
2 D
O
1 1 1
所以AO⋅(AB+AC)= ⃗AB2+ ⃗AC2= (b2+c2 )
2 2 2 B C
由余弦定理得b2+⃗c2-bc=3
3
学科网(北京)股份有限公司因为b2+⃗c2≥2bc
所以b2+⃗c2≤6,当且仅当b=c=√3是取等号
所以AO⋅(AB+AC) 的最大值为3
故答案为:3
15.(13分)
16.(15分)
4
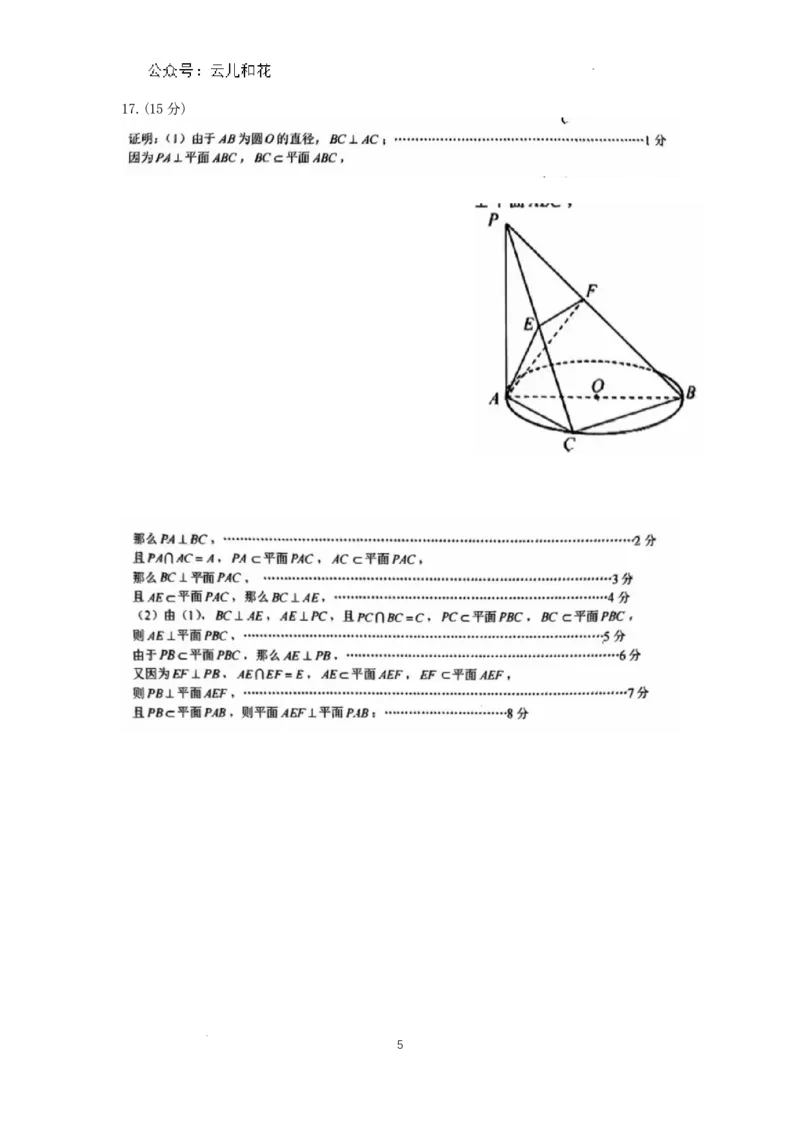
学科网(北京)股份有限公司17.(15分)
5
学科网(北京)股份有限公司18.(17分)
6
学科网(北京)股份有限公司7
学科网(北京)股份有限公司I9.(17分)
8
学科网(北京)股份有限公司9
学科网(北京)股份有限公司