文档内容
期末模拟卷5
一.选择题(共8小题)
1.复数z满足 •(1+2i)=4+3i,则z等于( )
A.2﹣i B.2+i C.1+2i D.1﹣2i
【分析】利用复数的运算法则、共轭复数的定义即可得出.
【解答】解:∵ •(1+2i)=4+3i,
∴ = = =2﹣i,
∴z=2+i.
故选:B.
2.某制药厂正在测试一种减肥药的疗效,有 1000名志愿者服用此药,体重变化结果统计
如表:
体重变化 体重减轻 体重不变 体重增加
人数 600 200 200
如果另有一人服用此药,估计这个人体重减轻的概率约为( )
A.0.1 B.0.2 C.0.5 D.0.6
【分析】用样本的数字特征估计总体的数字特征,可得结论.
【解答】解:由题意可得,这个人体重减轻的概率约为 =0.6,
故选:D.
3.若圆锥W的底面半径与高均为1,则圆锥W的表面积等于( )
A. B. C.2 D.
【分析】求出圆锥的母线长,再计算圆锥的侧面积π和表面积.
【解答】解:圆锥的轴截面如图所示,
则圆锥的母线为l= = ,所以该圆锥的侧面积为S侧面积 = rl= •1• = ,
π π π
圆锥的表面积为S表面积 =S侧面积+S底面积 = + •12=( +1) .
π π π
故选:A.
4.不透明的口袋内装有红色、绿色和蓝色卡片各2张,一次任意取出2张卡片,则与事件
“2张卡片都为红色”互斥而不对立的事件有( )
A.2张卡片都不是红色
B.2张卡片不都是红色
C.2张卡片至少有一张红色
D.2张卡片至多有1张红色
【分析】利用互斥事件、对立事件的定义直接判断.
【解答】解:不透明的口袋内装有红色、绿色和蓝色卡片各 2张,一次任意取出2张卡
片,
对于A,2张卡片都不是红色与事件“2张卡片都为红色”互斥而不对立的事件,故A正
确;
对于B,2张卡片不都是红色与事件“2张卡片都为红色”是对立的事件,故B错误;
对于C,2张卡片至少有一张红色与事件“2张卡片都为红色”能同时发生,不是互斥
事件,故C错误;
对于D,2张卡片至多有1张红色现事件“2张卡片都为红色”是对立事件,故D错误.
故选:A.
5.△ABC的内角A,B,C的对边分别为a,b,c.若A=45°,B=60°, ,则b的值
为( )
A. B. C. D.
【分析】由已知利用正弦定理即可求解.
【解答】解:因为A=45°,B=60°, ,
所以由正弦定理 ,可得b= = = .
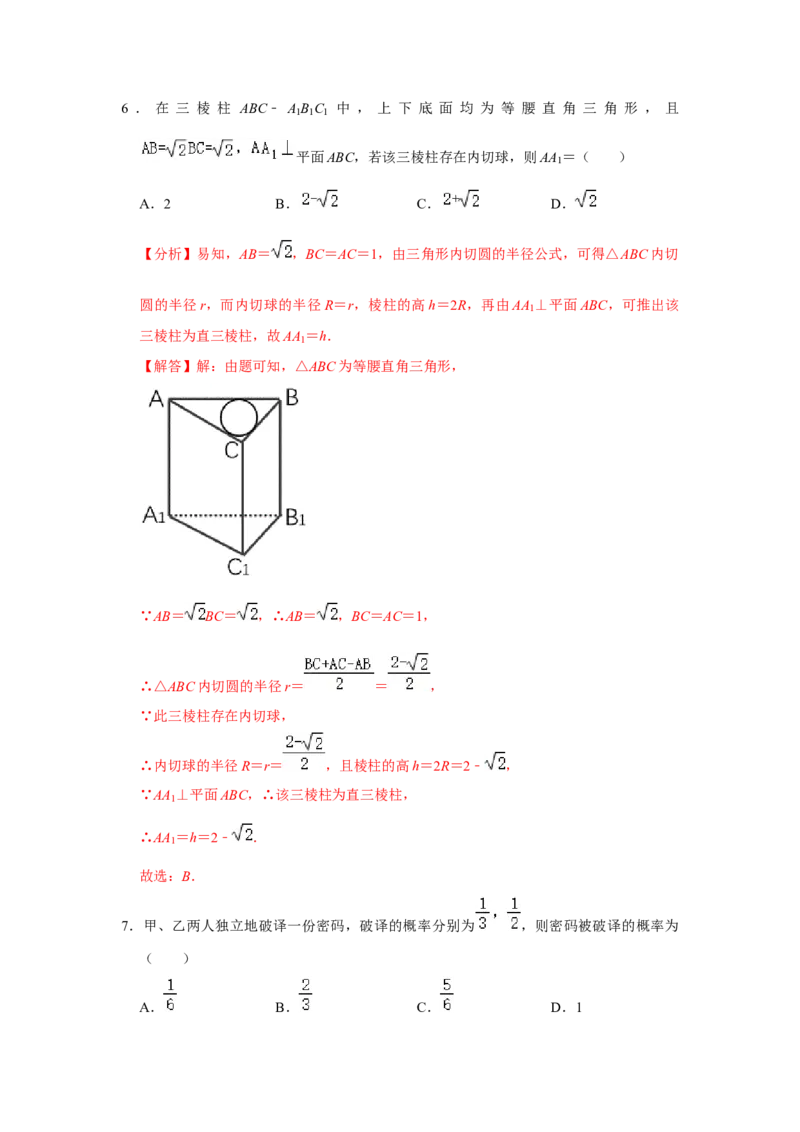
故选:B.6 . 在 三 棱 柱 ABC﹣ A B C 中 , 上 下 底 面 均 为 等 腰 直 角 三 角 形 , 且
1 1 1
平面ABC,若该三棱柱存在内切球,则AA =( )
1
A.2 B. C. D.
【分析】易知,AB= ,BC=AC=1,由三角形内切圆的半径公式,可得△ABC内切
圆的半径r,而内切球的半径R=r,棱柱的高h=2R,再由AA ⊥平面ABC,可推出该
1
三棱柱为直三棱柱,故AA =h.
1
【解答】解:由题可知,△ABC为等腰直角三角形,
∵AB= BC= ,∴AB= ,BC=AC=1,
∴△ABC内切圆的半径r= = ,
∵此三棱柱存在内切球,
∴内切球的半径R=r= ,且棱柱的高h=2R=2﹣ ,
∵AA ⊥平面ABC,∴该三棱柱为直三棱柱,
1
∴AA =h=2﹣ .
1
故选:B.
7.甲、乙两人独立地破译一份密码,破译的概率分别为 ,则密码被破译的概率为
( )
A. B. C. D.1【分析】密码被破译的对立事件是甲、乙同时不能破译密码,由此利用对立事件概率计
算公式和相互独立事件概率乘法公式能求出密码被破译的概率.
【解答】解:甲、乙两人独立地破译一份密码,
设事件A表示甲能破译密码,事件B表示乙能破译密码,
则P(A)= ,P(B)= ,
密码被破译的对立事件是甲、乙同时不能破译密码,
∴密码被破译的概率为:
P=1﹣P( )=1﹣P( )P( )
=1﹣(1﹣ )(1﹣ )
= .
故选:B.
8.设m、n是两条不同的直线, 、 是两个不同的平面,下列命题中错误的是( )
A.若m⊥ ,m∥n,n∥ ,则α ⊥β B.若 ⊥ ,m ,m⊥ ,则m∥
C.若m⊥α,m ,则 β⊥ α β D.若α⊥β,m⊄α,n β,则m⊥nα
【分析】利β用空⊂间α中线线α、β线面、面面间的位置关系α求解β . ⊂α ⊂β
【解答】解:若m⊥ ,m∥n,n∥ ,
则由平面与平面垂直α的判定定理得β⊥ ,故A正确;
若 ⊥ ,m ,m⊥ ,则由直线与α平面β 平行的判定定理得m∥ ,故B正确;
若αm⊥β,m⊄α,则由β平面与平面垂直的判定定理得 ⊥ ,故Cα正确;
若 ⊥β,m⊂α,n ,则m与n相交、平行或异面,α故βD错误.
故选α:βD. ⊂α ⊂β
二.多选题(共4小题)
9.如图,在四棱锥B﹣ACDE中,AE∥CD,CD=2AE,点M,N分别为BE,BA的中点,
若DM∩CN=P,DE∩CA=Q,则下述正确的是( )A. B.直线DE与BC异面
C.MN∥CD D.B,P,Q三点共线
【分析】对于A, = ;对于B,由条件可知直线DE与BC是异面直线;
对于C,由MN∥AE,AE∥CD,得MN∥CD;对于D,B,P,Q是平面ABC和平面
BDE的公共点,从而B,P,Q三点共线.
【解答】解:在四棱锥B﹣ACDE中,AE∥CD,CD=2AE,
点M,N分别为BE,BA的中点,DM∩CN=P,DE∩CA=Q,
对于A, = ,故A错误;
对于B,DE 平面ACDE,BC∩平面ACDE于C,C DE,
∴由异面直线⊂判定定理得直线DE与BC是异面直线,∉故B正确;
对于C,∵点M,N分别为BE,BA的中点,∴MN∥AE,
∵AE∥CD,∴MN∥CD,故C正确;
对于D,∵DM∩CN=P,DE∩CA=Q,平面ABC∩平面BDE=B,
∴B,P,Q是平面ABC和平面BDE的公共点,
∴B,P,Q三点共线,故D正确.
故选:BCD.
10.某地区公共部门为了调查本地区中学生的吸烟情况,对随机抽出的编号为 1~1000的
1000名学生进行了调查.调查中使用了两个问题,问题1:您的编号是否为奇数?问题
2:您是否吸烟?被调查者随机从设计好的随机装置(内有除颜色外完全相同的白球100
个,红球100个)中摸出一个小球:若摸出白球则回答问题 1,若摸出红球则回答问题
2,共有270人回答“是”,则下述正确的是( )
A.估计被调查者中约有520人吸烟B.估计约有20人对问题2的回答为“是”
C.估计该地区约有4%的中学生吸烟
D.估计该地区约有2%的中学生吸烟
【分析】根据题意知被调查者回答第一个问题的概率为 ,其编号是奇数的概率也是 ,
计算可得随机抽出的1000名学生中回答第一个问题且为“是”的学生数,
由此求出回答第二个问题且为是的人数,由此估计此地区中学生吸烟人数的百分比,进
而估计出被调查者中吸烟的人数,判断选项可得结论.
【解答】解:随机抽出的1000名学生中,回答第一个问题的概率是 ,
其编号是奇数的概率也是 ,
所以回答问题1且回答是的人数为1000× × =250;
所以回答第二个问题,且为是的人数270﹣250=20;
由此估计此地区中学生吸烟人数的百分比为 =4%.
估计被调查者中约有1000×4%=40人吸烟.
故表述正确的是BC.
故选:BC.
11.△ABC中,D为边AC上的一点,且满足 ,若P为边BD上的一点,且满足
(m>0,n>0),则下列结论正确的是( )
A.m+2n=1 B.mn的最大值为
C. 的最小值为6+4 D.m2+9n2的最小值为
【分析】利用向量共线定理可得:m+3n=1,再利用基本不等式以及“乘1法”逐一判
断即可.
【解答】解:因为 ,所以 ,
所以 =m +3n ,因为B、P、D三点共线,所以m+3n=1,故A错误;
则3mn≤ = ,则mn≤ ,
即mn最大值为 ,当且仅当m=3n,即m= ,n= 时取等号,故B正确;
=( )(m+3n)= + +7≥4 +7,当且仅当 = 时取等号,
所以 的最小值为4 +7,故C错误;
m2+9n2=(m+3n)2﹣6mn=1﹣6mn≥1﹣6× = ,当且仅当m= ,n= 时取等号,
所以m2+9n2的最小值为 ,故D正确.
故选:BD.
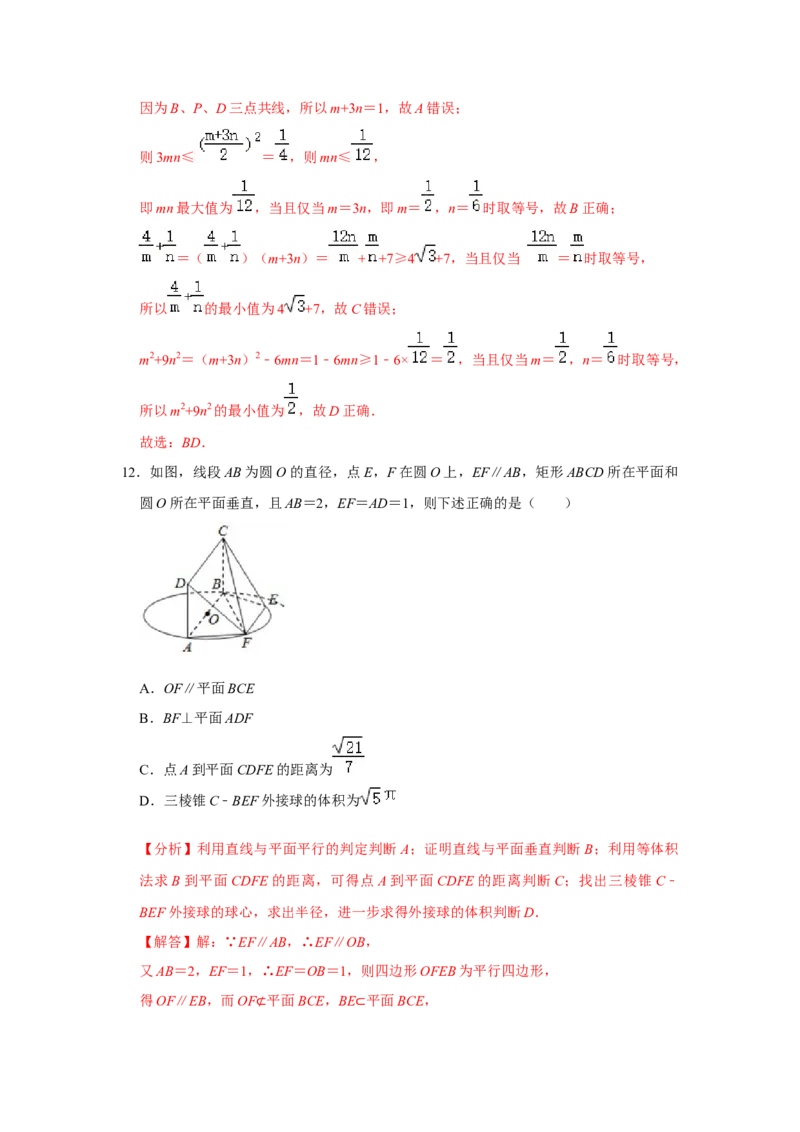
12.如图,线段AB为圆O的直径,点E,F在圆O上,EF∥AB,矩形ABCD所在平面和
圆O所在平面垂直,且AB=2,EF=AD=1,则下述正确的是( )
A.OF∥平面BCE
B.BF⊥平面ADF
C.点A到平面CDFE的距离为
D.三棱锥C﹣BEF外接球的体积为
【分析】利用直线与平面平行的判定判断 A;证明直线与平面垂直判断B;利用等体积
法求B到平面CDFE的距离,可得点A到平面CDFE的距离判断C;找出三棱锥C﹣
BEF外接球的球心,求出半径,进一步求得外接球的体积判断D.
【解答】解:∵EF∥AB,∴EF∥OB,
又AB=2,EF=1,∴EF=OB=1,则四边形OFEB为平行四边形,
得OF∥EB,而OF 平面BCE,BE 平面BCE,
⊄ ⊂∴OF∥平面BCE,故A正确;
∵DA⊥AB,平面ABCD⊥平面AFEB,且平面ABCD∩平面AFEB=AD,
∴AD⊥平面AFEB,则AD⊥BF,由BF⊥AF,AD∩AF=A,
∴BF⊥平面ADF,故B正确;
由AB∥EF,AB 平面CEF,EF 平面CEF,可得AB∥平面CEF.
则点A到平面C⊄DFE的距离等于⊂B到平面CDFE的距离.
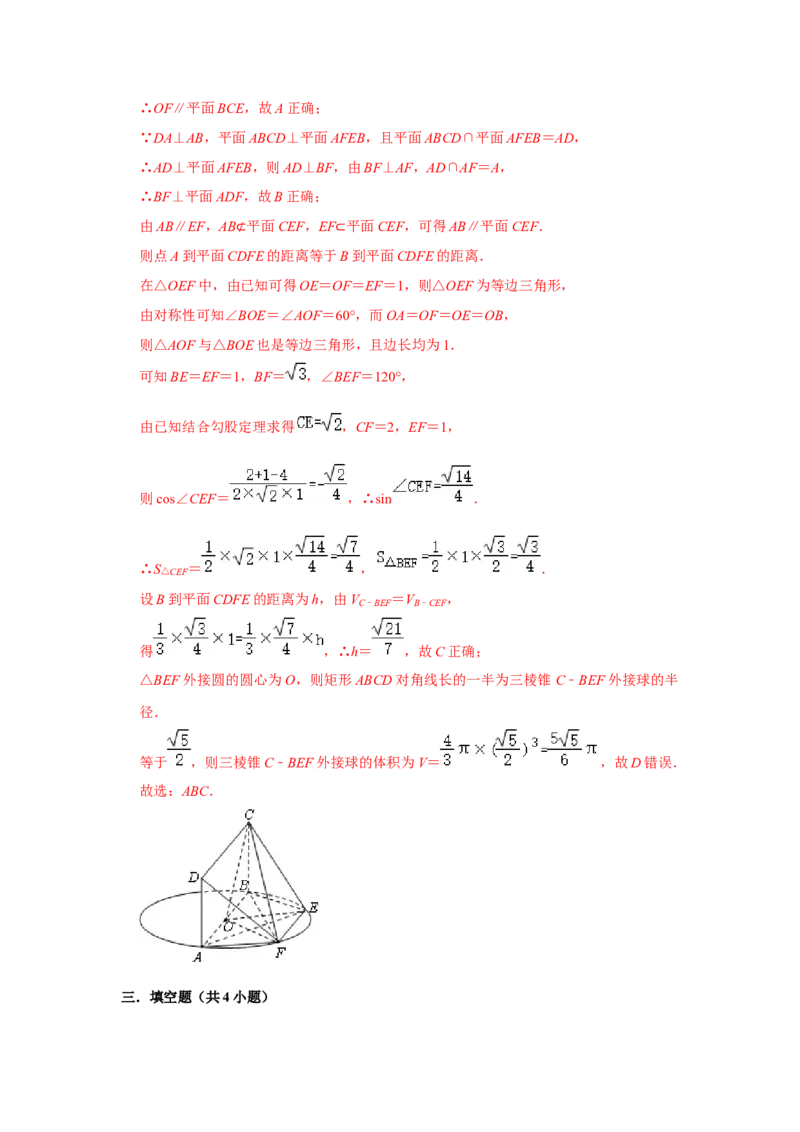
在△OEF中,由已知可得OE=OF=EF=1,则△OEF为等边三角形,
由对称性可知∠BOE=∠AOF=60°,而OA=OF=OE=OB,
则△AOF与△BOE也是等边三角形,且边长均为1.
可知BE=EF=1,BF= ,∠BEF=120°,
由已知结合勾股定理求得 ,CF=2,EF=1,
则cos∠CEF= ,∴sin .
∴S△CEF = , .
设B到平面CDFE的距离为h,由V
C﹣BEF
=V
B﹣CEF
,
得 ,∴h= ,故C正确;
△BEF外接圆的圆心为O,则矩形ABCD对角线长的一半为三棱锥C﹣BEF外接球的半
径.
等于 ,则三棱锥C﹣BEF外接球的体积为V= ,故D错误.
故选:ABC.
三.填空题(共4小题)13.向量 是单位向量,| |=2, ⊥ ,则| |= .
【分析】由题意可得 ,进行向量的模的运算带入求值即可得答案.
【解答】解:∵ ;
⇒
∴| |= = .
故答案为: .
14.正三棱柱ABC﹣A B C 的底面边长和高均为2,点D为侧棱CC 的中点,连接AD,
1 1 1 1
BD,则C D与平面ABD所成角的正弦值为 .
1
【分析】建立空间直角坐标系O﹣xyz,求出平面ABD的法向量,利用空间向量的数量
积求解C D与平面ABD所成角的正弦值即可.
1
【解答】解:如图,建立空间直角坐标系O﹣xyz,
O 为 A B 的中点,由已知,A(﹣1,0,2),B(1,0,2), ,
1 1
,
所以 , .
设平面ABD的法向量为 =(x,y,z),
由 ,令y=1,则z= ,
所以平面ABD的法向量为 = , ,则C D与平面ABD所成角的正弦值为: .
1
故答案为: .
15.设角 A,B,C 是△ABC 的三个内角,已知向量 ,
,且 .则角C的大小为 .
【分析】由已知结合向量数量积的坐标表示及正弦定理,余弦定理即可求解.
【解答】解:由已知可得, =sin2A﹣sin2C+sin2B﹣sinAsinB=0,
所以sin2A﹣sin2C+sin2B=sinAsinB,
由正弦定理可得,a2+b2﹣c2=ab,
所以cosC= = ,
因为C为三角形的内角,
所以C= ;
故答案为:
16.某人有3把钥匙,其中2把能打开门,如果随机地取一把钥匙试着开门,把不能打开
门的钥匙扔掉,那么第二次才能打开门的概率为 ;如果试过的钥匙又混进去,第
二次才能打开门的概率为 .
【分析】(1)第二次才能打开门是指第一次没有打开门,第二次打开门,由此利用相
互独立事件概率乘法公式能求出第二次才能打开门的概率;
(2)试过的钥匙又混进去,利用相互独立事件概率乘法公式能求出第二次才能打开门
的概率.
【解答】解:(1)某人有3把钥匙,其中2把能打开门,随机地取一把钥匙试着开门,
把不能打开门的钥匙扔掉,
第二次才能打开门是指第一次没有打开门,第二次打开门,∴第二次才能打开门的概率为P= = ;
(2)试过的钥匙又混进去,第二次才能打开门的概率为:P= = .
故答案为: , .
四.解答题(共6小题)
17.已知i是虚数单位,复数 .
(1)求|Z |,|Z |,|Z |,|Z |;
1 2 3 4
(2)随机从复数Z ,Z ,Z 中有放回的先后任取两个复数,求所取两个复数的模之积
2 3 4
等于1的概率.
【分析】(1)利用复数代数形式的乘除运算化简,再由复数模的计算公式求解|Z |,|
1
Z |,|Z |,|Z |;
2 3 4
(2)写出随机从复数Z ,Z ,Z 中有放回的先后任取两个复数的事件数,求出所取两
2 3 4
个复数的模之积等于1的事件数,再由古典概型概率公式求解.
【解答】解:(1)由题意知:|Z |=1, ,
1
,
;
(2)设随机从复数Z ,Z ,Z 中有放回的任取两个复数的样本点为(a,b),
2 3 4
则该随机试验的样本空间为 ={(Z ,Z ),(Z ,Z ),(Z ,Z ),(Z ,Z ),
2 2 2 3 2 4 3 2
(Z ,Z ),(Z ,Z ),(ΩZ ,Z ),(Z ,Z ),(Z ,Z )}
3 3 3 4 4 2 4 3 4 4
所以n( )=9,
设事件AΩ=“所取两个复数的模之积等于1”,
则事件A={(Z ,Z ),(Z ,Z ),(Z ,Z ),(Z ,Z )},
2 4 3 4 4 2 4 3
∴n(A)=4,故 .
18.已知在四面体ABCD中,AB=AC,DB=DC,点E,F,G,M分别为棱AD,BD,
DC,BC上的点,且BM=MC,DF=2FB,DG=2GC,AE= AD(0≤ ≤1).
λ λ(Ⅰ)当 = 时,求证:AM∥平面EFG;
(Ⅱ)当λ变化时,求证:平面ADM⊥平面EFG.
λ
【分析】(Ⅰ)当 = 时, ,推导出EF∥AB,EG∥AC,从而平面ABC∥平
面EFG,由此能证明λ AM∥平面EFG.
(Ⅱ)推导出AM⊥BC,DM⊥BC,BC∥GF,从而BC⊥平面ADM,GF⊥平面ADM,
由此能证明当 变化时,平面ADM⊥平面EFG.
λ
【解答】证明:(Ⅰ)当 = 时, ,
∵四面体ABCD中,AB=λAC,DB=DC,
点E,F,G,M分别为棱AD,BD,DC,BC上的点,BM=MC,DF=2FB,DG=
2GC,
∴EF∥AB,EG∥AC,又EF∩EG=E,AB∩AC=A,
∴平面ABC∥平面EFG,
∵AM 平面ABC,∴AM∥平面EFG.
(Ⅱ)⊂∵AB=AC,DB=DC,点E,F,G,M分别为棱AD,BD,DC,BC上的点,
BM=MC,DF=2FB,DG=2GC,AE= AD(0≤ ≤1).
∴AM⊥BC,DM⊥BC,BC∥GF, λ λ
∵AM∩DM=M,∴BC⊥平面ADM,
∵GF∥BC,∴GF⊥平面ADM,
∵GF 平面EFG,
∴当 ⊂变化时,平面ADM⊥平面EFG.
λ
19.在① ;② 这两个条件中任选一个,补充到下面问题
中,并进行作答.在△ABC 中,内角 A,B,C 的对边分别为 a,b,c, , ,
______.
(1)求角A,B,C的大小;
(2)求△ABC的周长和面积.
【分析】(1)若选择①:利用三角函数恒等变换的应用,结合范围 B+C (0, ),
∈ π
可求 , ,利用两角差的余弦函数公式可求 cos(B﹣C)=1,结合
,可求B﹣C=0,可得 ;
若 选 择 ② : ( 法 一 ) 由 题 意 , 利 用 基 本 不 等 式 可 求
,可得 ,利用三角形的内角和定理可求A
的值;
(法二)设tanB,tanC为方程, 的两根,利用一元二次方程的解法可
得 ,且B,C (0, ),可求 ,利用三角形的内角和定理可
求A的值; ∈ π
(2)由正弦定理可求b=c=2,利用三角形的面积公式即可求解.
【解答】解:(1)若选择①:
因为 , ,所以 (2分)
所以 ,
因为B+C (0, ),所以 , (4分)
∈ π
又因为cos(B﹣C)=cosBcosC+sinBsinC=1,
所以B﹣C=0, (6分)
若选择②:
(法一)由题意知,tanB>0,tanC>0,所以 (2分)
因为当且仅当 时,上式的等号成立,且B,C (0, )(3分)
∈ π
所以 (5分)
所以 (6分)
(法二)设tanB,tanC为方程, 的两根(2分)
解得 ,且B,C (0, )(4分)
∈ π
所以 (5分)
所以 (6分)
(2)由正弦定理知: (7分)
因为 , ,
所以b=c=2(9分)
所以△ABC的周长为 (10分)
所以△ABC的面积 (12分)
20.如图1,△ABC是等腰直角三角形∠CAB=90°,AC=2a,E,F分别为AC,BC的中
点,沿EF将△CEF折起,得到如图2所示的四棱锥C′﹣ABFE
(Ⅰ)求证:AB⊥平面AEC′;
(Ⅱ)当四棱锥C′﹣ABFE体积取最大值时,
(i)若G为BC′中点,求异面直线GF与AC′所成角;
(ii)在C′﹣ABFE中AE交BF于C,求二面角A﹣CC′﹣B的余弦值.【分析】(Ⅰ)推导出EF⊥AE,EF⊥C'E,从而EF⊥平面AEC',由此能证明AB⊥平
面AEC'.
(Ⅱ)(i)取AC'中点D,连接DE,EF,FG,GD,推导出四边形DEFG 为平行四边
形,直线GF 与AC'所成角就是DE 与AC'所成角,由此能求出直线GF 与AC'所成角.
(ii) 分别以EA、EF、EC'所在直线为x 轴、y 轴、z 轴,建立空间直角坐标系,利用
向量法能求出平面C'AE与平面C'BF的平面角的夹角的余弦值.
【解答】证明:(Ⅰ)因为△ABC 是等腰直角三角形,∠CAB=90°,E,F 分别为
AC,BC 的中点,
所以EF⊥AE,EF⊥C'E.
又因为AE∩C'E=E,所以EF⊥平面AEC'.
由于EF∥AB,所以有AB⊥平面AEC'.4分
解:(Ⅱ)(i)取AC'中点D,连接DE,EF,FG,GD,
由于GD 为△ABC'中位线,以及EF 为△ABC 中位线,
所以四边形DEFG 为平行四边形.
直线GF 与AC'所成角就是DE 与AC'所成角.
所以四棱锥C'﹣ABFE 体积取最大值时,C'E 垂直于底面ABFE.
此时△AEC'为等腰直角三角形,
ED 为中线,所以直线ED⊥AC'.
又因为ED∥GF,所以直线GF 与AC'所成角为 .10分
(ii) 因为四棱锥C'﹣ABFE 体积取最大值,
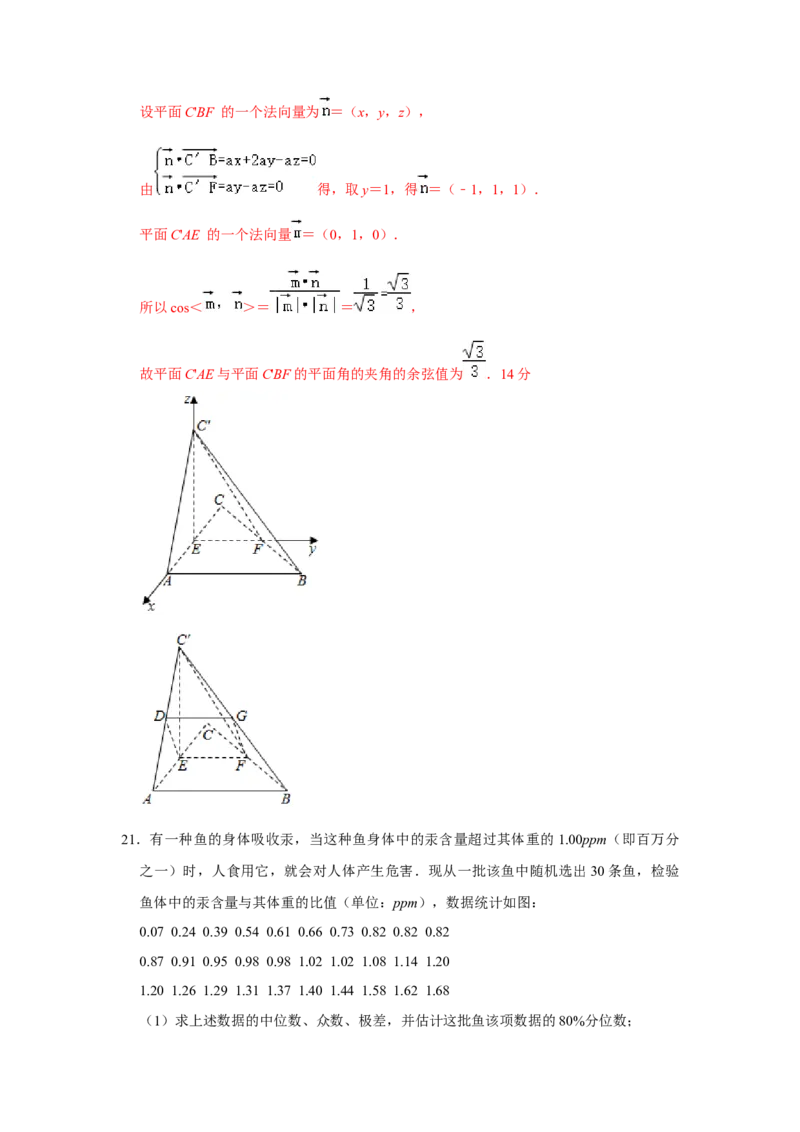
分别以EA、EF、EC'所在直线为x 轴、y 轴、z 轴,建立空间直角坐标系如图,
则C'(0,0,a),B(a,2a,0),F(0,a,0),C'B(a,2a,﹣a),C'F(0,a,
﹣a).设平面C'BF 的一个法向量为 =(x,y,z),
由 得,取y=1,得 =(﹣1,1,1).
平面C'AE 的一个法向量 =(0,1,0).
所以cos< >= = ,
故平面C'AE与平面C'BF的平面角的夹角的余弦值为 .14分
21.有一种鱼的身体吸收汞,当这种鱼身体中的汞含量超过其体重的1.00ppm(即百万分
之一)时,人食用它,就会对人体产生危害.现从一批该鱼中随机选出30条鱼,检验
鱼体中的汞含量与其体重的比值(单位:ppm),数据统计如图:
0.07 0.24 0.39 0.54 0.61 0.66 0.73 0.82 0.82 0.82
0.87 0.91 0.95 0.98 0.98 1.02 1.02 1.08 1.14 1.20
1.20 1.26 1.29 1.31 1.37 1.40 1.44 1.58 1.62 1.68
(1)求上述数据的中位数、众数、极差,并估计这批鱼该项数据的80%分位数;(2)有A,B两个水池,两水池之间有10个完全相同的小孔联通,所有的小孔均在水
下,且可以同时通过2条鱼.
(ⅰ)将其中汞的含量最低的2条鱼分别放入A水池和B水池中,若这2条鱼的游动相
互独立,均有 的概率进入另一水池且不再游回,求这两条鱼最终在同一水池的概率;
(ⅱ)将其中汞的含量最低的2条鱼都先放入A水池中,若这2条鱼均会独立地且等可
能地从其中任意一个小孔由A水池进入B水池且不再游回A水池,求这两条鱼由不同小
孔进入B水池的概率.
【分析】(1)由所给数据能求出数据的中位数,数据的众数,数据的极差,能估计这
批鱼该项数据的80百分位数.
(2)(ⅰ)记“两鱼最终均在A水池”为事件A,记“两鱼最终均在B水池”为事件
B,利用相互独立事件概率乘法公式求出P(A),P(B),由事件A与事件B互斥,
能求出两条鱼最终在同一水池的概率.
(ⅱ)记“两鱼同时从第一个小孔通过”为事件C ,“两鱼同时从第二个小孔通过”为
1
事 件 C , … … 依 此 类 推 . 由 两 鱼 的 游 动 独 立 , 得 到
2
,由事件 C ,事件 C ,……互斥,得到
1 2
,记“两条鱼由不同小孔进入 B 水
池”为事件C,由C与C ∪C ∪…∪C 对立,能求出这两条鱼由不同小孔进入B水池
1 2 10
的概率.
【解答】解:(1)由题意知,数据的中位数为 ,
数据的众数为0.82,
数据的极差为1.68﹣0.07=1.61,
估计这批鱼该项数据的80百分位数约为 ;
(2)(ⅰ)记“两鱼最终均在A水池”为事件A,则 ,
记“两鱼最终均在B水池”为事件B,则 ,
因为事件A与事件B互斥,所以两条鱼最终在同一水池的概率为 .
(ⅱ)记“两鱼同时从第一个小孔通过”为事件C ,
1
“两鱼同时从第二个小孔通过”为事件C ,……依此类推.
2
因为两鱼的游动独立,所以 ,
因为事件C ,事件C ,……互斥,
1 2
所以 ,
记“两条鱼由不同小孔进入B水池”为事件C,
则C与C ∪C ∪…∪C 对立,
1 2 10
所以 .
22.某学校高一100名学生参加数学竞赛,成绩均在40分到100分之间.学生成绩的频率
分布直方图如图:
(1)估计这100名学生分数的中位数与平均数;(精确到0.1)
(2)某老师抽取了10名学生的分数:x ,x ,x ,…,x ,已知这10个分数的平均数
1 2 3 10
,标准差s=6,若剔除其中的100和80两个分数,求剩余8个分数的平均数与标
准差.
(参考公式: )
(3)该学校有3座构造相同教学楼,各教学楼高均为20米,东西长均为60米,南北宽
均为20米.其中1号教学楼在2号教学楼的正南且楼距为40米,3号教学楼在2号教学
楼的正东且楼距为72米.现有3种型号的考试屏蔽仪,它们的信号覆盖半径依次为
35,55,105米,每个售价相应依次为1500,2000,4000元.若屏蔽仪可在地下及地上
任意位置安装且每个安装费用均为100元,求让各教学楼均被屏蔽仪信号完全覆盖的最
小花费.
(参考数据:2102=44100,1922=36864,1102=12100)【分析】(1)利用频率分布直方图能求出中位数、平均分.
(2)由题意,求出剩余8个分数的平均值,由10个分数的标准差,能求出剩余8个分
数的标准差.
(3)求出将3座教学楼完全包裹的球的最小直径、将一座教学楼完全包裹的球的最小
直径和将1号教学楼与2号教学楼完全包裹的球的最小直径,由此能求出让各教学楼均
被屏蔽仪信号完全覆盖的最小花费.
【解答】解:(1)因为0.05+0.15+0.25=0.45<0.50.05+0.15+0.25+0.35=0.8>0.5
所以中位数为x满足70<x<80,
由 ,解得 ,
设平均分为y,
则y=0.05×45+0.15×55+0.25×65+0.35×75+0.1×85+0.1×95=71.
(2)由题意,剩余8个分数的平均值为 ,
因为10个分数的标准差
所以 ,
所 以 剩 余 8 个 分 数 的 标 准 差 为 =
.
( 3 ) 将 3 座 教 学 楼 完 全 包 裹 的 球 的 最 小 直 径 为 :因此若用一个覆盖半径为105米的屏蔽仪则总费用为4100元,
将一座教学楼完全包裹的球的最小直径为
因此若用3个覆盖半径为35米的屏蔽仪则总费用为4800元,
将 1 号 教 学 楼 与 2 号 教 学 楼 完 全 包 裹 的 球 的 最 小 直 径 为 :
又因为
因此若用1个覆盖半径为55米和1个覆盖半径为35米的屏蔽仪则总费用为3700元;
所以,让各教学楼均被屏蔽仪信号完全覆盖的最小花费为3700元.