文档内容
第六章 平面向量及其应用A(基础卷)
试卷副标题
考试范围:xxx;考试时间:100分钟;命题人:xxx
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 四 总分
得分
第Ⅰ卷(选择题)
请点击修改第I卷的文字说明
评卷人 得 分
一.选择题(共8小题)
1.(2019秋•公安县期末)如果向量 (0,1), (﹣2,1),那么| 2 |=( )
A.6 B.5 C.4 D.3
2.(2020•葫芦岛模拟)在矩形ABCD中,AB=1,AD ,点M在对角线AC上,点N在边CD上,且
, ,则 ( )
A. B.4 C. D.
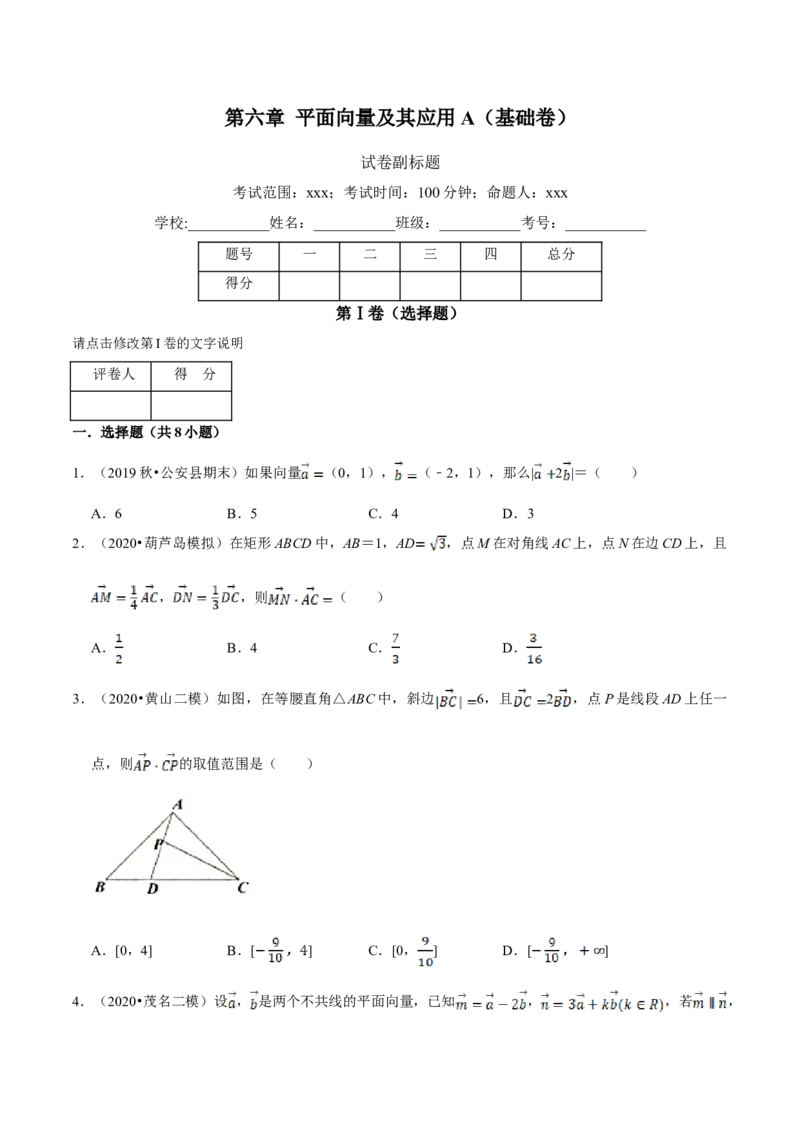
3.(2020•黄山二模)如图,在等腰直角△ABC中,斜边 6,且 2 ,点P是线段AD上任一
点,则 的取值范围是( )
A.[0,4] B.[ ] C.[0, ] D.[ ]
4.(2020•茂名二模)设 , 是两个不共线的平面向量,已知 , ,若 ,则k=( )
A.2 B.﹣2 C.6 D.﹣6
5.(2020春•扬州期末)已知△ABC的内角A,B,C的对边分别为a,b,c,若A=60°,a ,则
等于( )
A. B. C. D.2
6.(2020春•房山区期末)在△ABC中,角A,B,C所对的边分别为a,b,c,如果a=2,A=45°,B=
30°,那么b=( )
A. B. C. D.
7.(2020•罗湖区校级模拟)海伦公式是利用三角形的三条边的边长a,b,c直接求三角形面积S的公式,
表达式为:S ,p ;它的特点是形式漂亮,便于记忆.中国宋代的数
学家秦九韶在1247年独立提出了“三斜求积术”,虽然它与海伦公式形式上有所不同,但它与海伦公
式完全等价,因此海伦公式又译作海伦﹣秦九韶公式.现在有周长为 10+2 的△ABC满足sinA:
sinB:sinC=2:3: ,则用以上给出的公式求得△ABC的面积为( )
A. B. C. D.12
8.(2020•山西模拟)已知向量 , , ,则当 取最小值时,实数t
=( )
A. B. C. D.第Ⅱ卷(非选择题)
请点击修改第Ⅱ卷的文字说明
评卷人 得 分
二.多选题(共4小题)
9.(2020春•江阴市期中)在△ABC中, ,AC=1, ,则角A的可能取值为( )
A. B. C. D.
10.(2020•青岛模拟)已知△ABC的面积为3,在△ABC所在的平面内有两点P,Q,满足 2
, ,记△APQ的面积为S,则下列说法正确的是( )
A. ∥ B.
C. D.S=4
11.(2020春•正定县校级月考)以下关于正弦定理或其变形正确的有( )
A.在△ABC中,a:b:c=sin A:sin B:sin C
B.在△ABC中,若sin 2A=sin 2B,则a=b
C.在△ABC中,若sin A>sin B,则A>B,若A>B,则sin A>sin B都成立
D.在△ABC中,
12.(2020•泰安模拟)已知向量 (2,1), (1,﹣1), (m﹣2,﹣n),其中m,n均为正
数,且( )∥ ,下列说法正确的是( )
A.a与b的夹角为钝角
B.向量a在b方向上的投影为
C.2m+n=4
D.mn的最大值为2评卷人 得 分
三.填空题(共4小题)
13.(2020•新课标Ⅰ)设向量 (1,﹣1), (m+1,2m﹣4),若 ⊥ ,则m= .
14.(2020•新课标Ⅰ)设 , 为单位向量,且| |=1,则| |= .
15.(2020•葫芦岛模拟)若tan ,向量 (1,﹣1), (cos2 ,sin2 ),则 • .
α α α
16.(2020春•房山区期末)在△ABC中,角A,B,C所对的边分别为a,b,c,如果a=3,b ,c=
2 ,那么cosA= .
评卷人 得 分
四.解答题(共5小题)
17.(2020春•胶州市期中)已知 , R.
α∈
(1)若向量 ,求 的值;
(2)若向量 ,证明: .
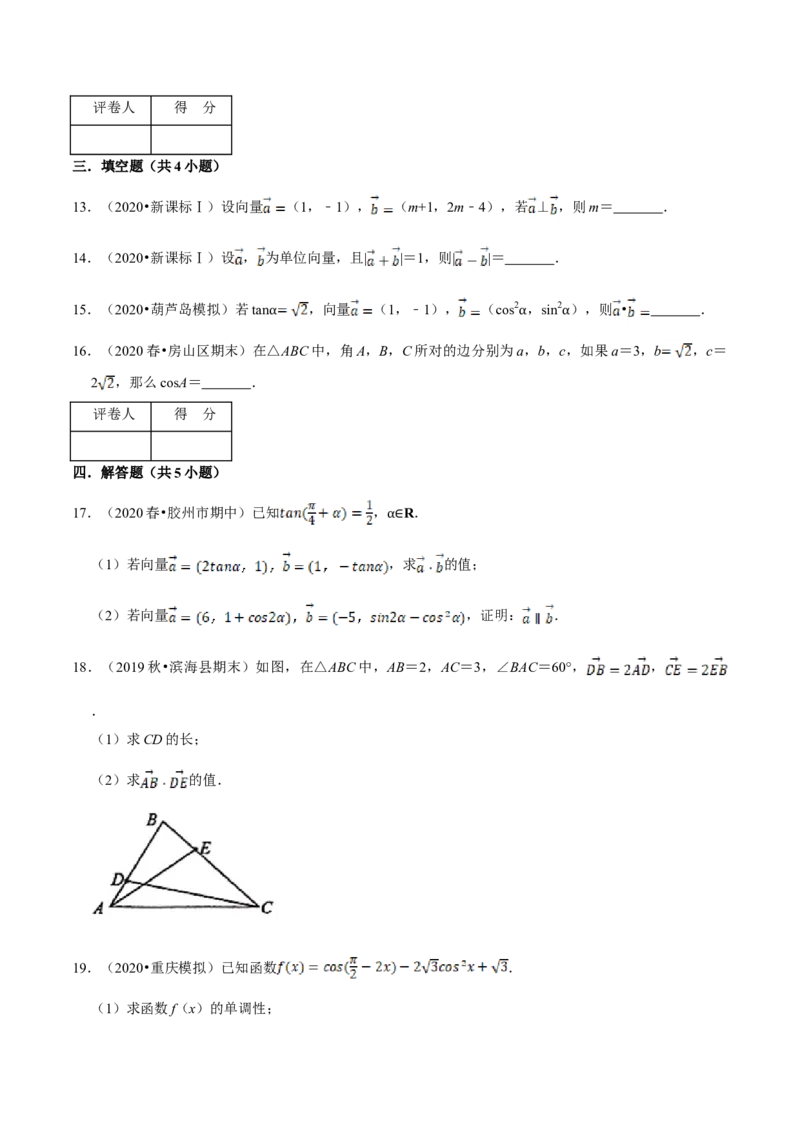
18.(2019秋•滨海县期末)如图,在△ABC中,AB=2,AC=3,∠BAC=60°, ,
.
(1)求CD的长;
(2)求 的值.
19.(2020•重庆模拟)已知函数 .
(1)求函数f(x)的单调性;(2)在△ABC中,角A,B,C的对边分别为a,b,c,且 , ,c=1,求△ABC的面积.
20.(2019 秋•安徽期末)在△ABC 中,内角 A,B,C 的对边分别为 a,b,c,设平面向量
,且
(Ⅰ)求C;
(Ⅱ)若 ,求△ABC中AB边上的高h.
21.(2020•山东模拟)在 a , (2a﹣b)sinA+(2b﹣a)sinB=2csinC这两个条件
中任选一个,补充在下列①问题中,并解答. ②
已知△ABC的角A,B,C对边分别为a,b,c,c 而且 _______.
(1)求∠C;
(2)求△ABC周长的最大值.