文档内容
2024-2025学年春期高一数学月考模拟
考试范围:第一章;
一、单选题
1.集合 中角 的终边在单位圆中的位置(阴影部
分)是( )
A B C D
2.将函数 图象向右平移 个单位得到奇函数,则 的最小值为
( )
A. B. C. D.
3.智能主动降噪耳机工作的原理是通过耳机两端的噪声采集器采集周围的噪声,然后通过
主动降噪芯片生成与噪声相位相反、振幅相同的声波来抵消噪声(如图).已知噪声的声
波曲线 (其中 , , )的振幅为1,周期为2π,初相为
,则通过主动降噪芯片生成的声波曲线的解析式为( ).
A. ; B. ; C. ; D. .
4.已知角 的终边过点 ,且 ,则 ( )
A.310° B.50° C.220° D.40°
5.已知△ABC为锐角三角形,设函数 ,则( )
A. B.C. D.
6.勒洛三角形是一种定宽曲线,它是德国机械工程专家勒洛首先进行研究的,其画法是:
先画一个正三角形,再以正三角形每个顶点为圆心,以边长为半径,在另两个顶点间作一
段弧,三段弧围成的曲边三角形就是勒洛三角形,如图所示,若正三角形 的边长为
2,则勒洛三角形的面积为( )
A. B. C. D.
7.函数 的图象如图所示,直线 经过函数
图象的最高点M和最低点N,则 ( )
A.0 B. C. D.
8.将函数 的图象向左平移 个单位长度得到函数 的
图象,如图所示,图中阴影部分的面积为 ,则 ( )
A. B. C. D.
二、多选题
9.下列说法正确的有( )
√2
A.若 是锐角,则 是第一象限角 B.“x= ”是“sinx= ”的充分不必要
2条件
C.若 ,则 为第一或第二象限角
D.小圆中1弧度的圆心角比大圆中1弧度制的圆心角小
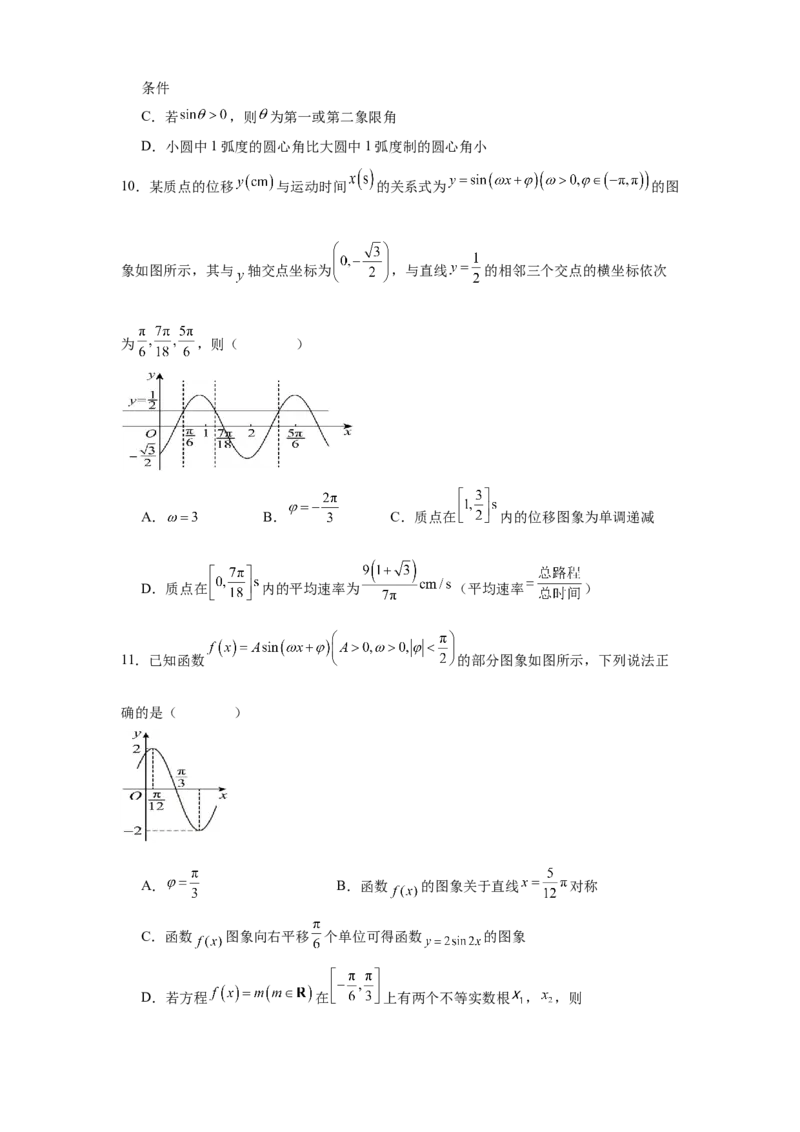
10.某质点的位移 与运动时间 的关系式为 的图
象如图所示,其与 轴交点坐标为 ,与直线 的相邻三个交点的横坐标依次
为 ,则( )
A. B. C.质点在 内的位移图象为单调递减
D.质点在 内的平均速率为 (平均速率 )
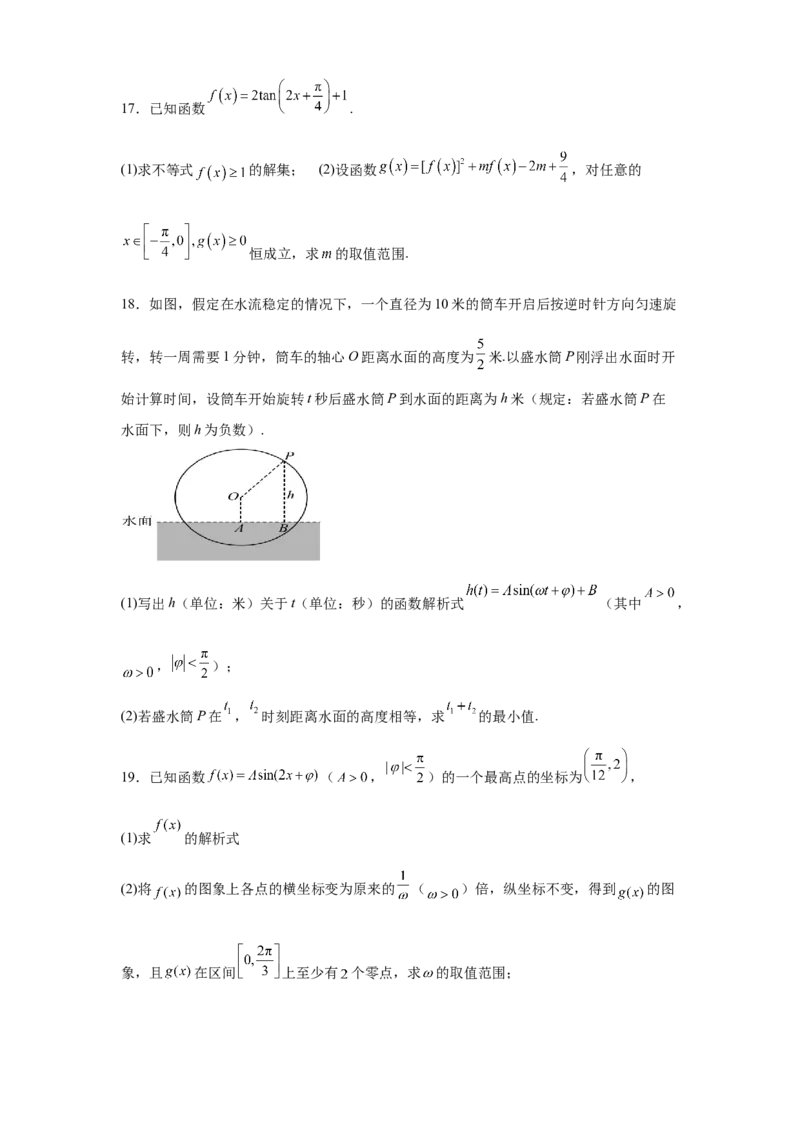
11.已知函数 的部分图象如图所示,下列说法正
确的是( )
A. B.函数 的图象关于直线 对称
C.函数 图象向右平移 个单位可得函数 的图象
D.若方程 在 上有两个不等实数根 , ,则三、填空题
12.设函数 ( 是常数, ). 若 在区间 上
具有单调性,且 , 则 的最小正周期为 .
13.奇函数 的定义域为 ,若 为偶函数,且 ,则
.
14.设函数 ,若 为函数 的零点, 为函数
的图象的对称轴,且 在区间 上单调,则 的最大值为 .
四、解答题
15.在平面直角坐标系 中,锐角 的顶点是坐标原点,始边与x轴正半轴重合,终边
交单位圆于点 .将角 的终边按逆时针方向旋转 得到角 .
(1)求 ; (2)求 的值.
16.已知函数 ,当 时, 的最大值为 .
(1)求函数 在 上的单调区间;
(2)若 且满足 ,求 的取值集合17.已知函数 .
(1)求不等式 的解集; (2)设函数 ,对任意的
恒成立,求 的取值范围.
18.如图,假定在水流稳定的情况下,一个直径为10米的筒车开启后按逆时针方向匀速旋
转,转一周需要1分钟,筒车的轴心O距离水面的高度为 米.以盛水筒P刚浮出水面时开
始计算时间,设筒车开始旋转t秒后盛水筒P到水面的距离为h米(规定:若盛水筒P在
水面下,则h为负数).
(1)写出h(单位:米)关于t(单位:秒)的函数解析式 (其中 ,
, );
(2)若盛水筒P在 , 时刻距离水面的高度相等,求 的最小值.
19.已知函数 ( , )的一个最高点的坐标为 ,
(1)求 的解析式
(2)将 的图象上各点的横坐标变为原来的 ( )倍,纵坐标不变,得到 的图
象,且 在区间 上至少有 个零点,求 的取值范围;(3)在(2)的条件下,当 取得最小值时,对 ,都有
成立,求 的取值范围.2024-2025学年春期高一数学月考模拟参考答案
1.C 2.B 3.D 4.A 5.B 6.B 7.D 8.A 9.AB 10.AC
11.ACD
15 3
12、 π 13、-2 14、 /3
4 4
1 2√2 2√2
15、(1) − (2)−
3 3 7
16、 的单调递增区间为[ π],减区间[π π] x 的取值集合为
f(x) 0 , ,
6 6 2
{ π π π 5π}
− , − , ,
2 6 2 6
17、 ;
18、 ; 。
19、 ; ; 。