文档内容
2024-2025 学年辽宁省鞍山市高一下学期期中考试
数学试卷 B
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.−1600°的终边在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2.如图1,这是杭州第19届亚运会会徽,名为“潮涌”,如图2,这是“潮涌”的平面图,若OA=2OB,
则图形ABCD的面积与扇形AOD的面积的比值是( )
1 1 2 3
A. B. C. D.
4 3 3 4
cosα √3
3.若 = ,则tanα=( )
cosα−sinα 3
√3 √3
A. 1− B. 1−√3 C. D. 1+√3
3 3
π 3
4.在▵ABC中,角A,B,C的对边长分别为a,b,c.若A= ,cosB= ,a=5,则c=( )
4 5
A. 10 B. 7 C. 4 D. 3
5.若 ( π) 1,则 ( π) ( )
sin θ+ = cos θ− =
4 3 4
1 1 2√2 2√2
A. B. − C. D. −
3 3 3 3
6.在▵ABC中,内角A,B,C的对边分别为a,b,c,已知c=acosB,则▵ABC的形状为( )
A. 等腰三角形 B. 直角三角形 C. 等腰直角三角形 D. 等腰或直角三角形
7.已知向量 ⃗a 与⃗b 的夹角为 60° , |⃗a|=1 ,|⃗
b
|
=√3
,若⃗
a⊥
(
λ
⃗
a+
⃗
b
),则实数 λ=( )
第 页,共 页
1 1√3 4
A. − B. 1 C. − D. 2
2 3
2 1
8.已知cos(α+β)= ,cos(α−β)= ,则tanαtanβ=( )
3 3
1 1 1
A. −3 B. − C. − D. −
3 4 5
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.下列说法正确的是( )
A. 若α是第一象限角,则α是锐角
π
B. 3°= rad
60
C. 若sinθ<0,则θ为第三或第四象限角
θ
D. 若θ为第二象限角,则 为第一象限或第三象限角
2
1
10.下列代数式的值为 的是( )
4
tan15°
A. cos275°−sin275° B.
1+tan215°
C. cos36°cos72° D. 4sin10°sin30°sin50°sin70°
11.已知▵ABC的内角A,B,C的对边分别为a,b,c,则下列说法正确的是( )
A. 若sin A>sinB,则A>B
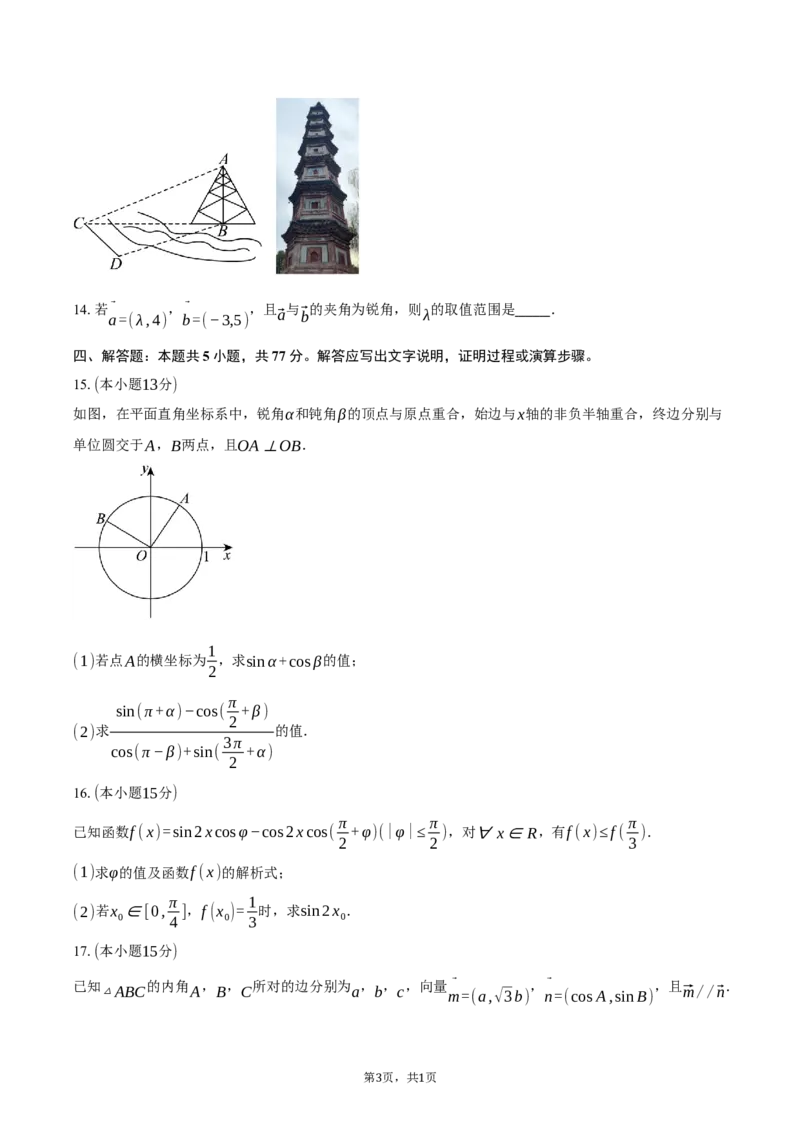
B. 若sin2A+sin2B0,ω>0,0<φ<π)在一个周期内的图象如图所示.
(1)求函数解析式;
(2)求f(x)的单调递增区间;
当 [ π π]时,求 的最大值和最小值.
(3) x∈ , f(x)
12 2
19.(本小题17分)
⃗ ⃗ ⃗ ⃗ 1
已知向量 a=(sinωx,cosωx) , b=(√3cosωx,−cosωx) ,ω>0,f(x)=a⋅b+ ,且f(x)的图象上相邻
2
π
两条对称轴之间的距离为 .
2
(1)求函数f(x)的解析式;
(2)求函数f(x)的单调递减区间;
若函数 在 [ π π]有三个不同的零点从小到大依次为 ,求
(3) y=[f(x)] 2 −(m+1)f(x)+m x∈ − , x ,x ,x
2 3 1 2 3
的值.
tan(x +x +2x )
1 2 3
第 页,共 页
4 1参考答案
1.C
2.D
3.B
4.B
5.A
6.B
7.A
8.B
9.BD
10.BCD
11.AD
3
12. /0.6
5
13.20√6−20√2
20 12
14.λ< 且λ≠− .
3 5
π
15.解:(1)由题意:β= +α,
2
π
所以sinα+cosβ=sinα+cos( +α)=sinα−sinα=0;
2
π π π
sin(π+α)−cos( +β) sin(π+α)−cos( + +α)
2 2 2 −sinα+cosα
(2) = = =−1.
3π π 3π sinα−cosα
cos(π−β)+sin( +α) cos(π− −α)+sin( +α)
2 2 2
16.(1)f(x)=sin2xcosφ+cos2xsinφ=sin(2x+φ),
π 2π
对∀x∈R,有f(x)≤f( ),则sin( +φ)=1,
3 3
2π π π π π
则 +φ= +2kπ,k∈Z,因|φ|≤ ,解得φ=− ,故f(x)=sin(2x− );
3 2 2 6 6
π 1 π π π π
(2)因f(x )=sin(2x − )= ,由x ∈[0, ],可得2x − ∈[− , ],
0 0 6 3 0 4 0 6 6 3
第 页,共 页
5 1则 π √ π √ 1 2 2√2,
cos(2x − )= 1−sin2 (2x − )= 1−( ) =
0 6 0 6 3 3
π π √3 π 1 π
故sin2x =sin(2x − + )= sin(2x − )+ cos(2x − )
0 0 6 6 2 0 6 2 0 6
√3 1 1 2√2 2√2+√3
= × + × = .
2 3 2 3 6
17.解: 向量⃗ ,⃗ ,
(1) m=(a,√3b) n=(cosA,sinB)
因为⃗m//⃗n,所以asinB−√3bcosA=0,
由正弦定理,得sin AsinB−√3sinBcosA=0,
∵B∈(0,π),∴sinB>0,
∴sin A=√3cosA,∴tan A=√3,
∵A∈(0,π),A为△ABC的内角,
π
所以A= ;
3
(2)由余弦定理,得a2=b2+c2−2bccosA,
已知 a=√13,b=3,
∴c2−3c−4=0,
∴(c−4)(c+1)=0,
因为c>0, ∴c=4,
1
则 S= bcsin A=3√3;
2
,
(3)∵a2=b2+c2−2bccosA
, ,
∴b2+c2=bc+4 ∴(b+c) 2=3bc+4
(b+c) 2
∵bc≤ ,
4
3(b+c) 2
∴(b+c) 2≤ +4,
4
第 页,共 页
6 1,
∴(b+c) 2≤16
∵b+c>0,∴b+c≤4,当且仅当b=c=2时,等号成立,
∴b+c的最大值为4.
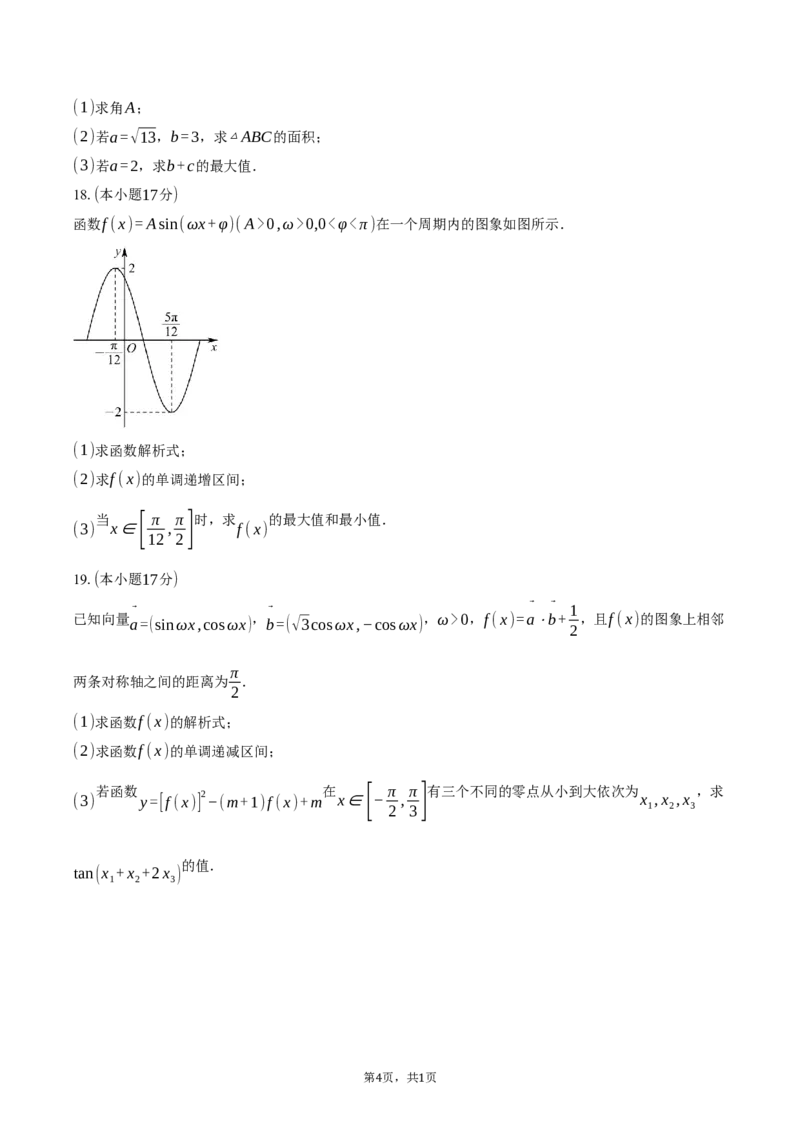
18.解: 由图象知 ,T 5π ( π ) π, 2π ,即 .
(1) A=2 = − − = ∴ =π ω=2
2 12 12 2 ω
由图象过点(5π ),代入函数 ,
,−2 f (x)
12
5π π 2π
即 +φ=− +2kπ,k∈Z,因为0<φ<π,则φ= ,
6 2 3
所以 ( 2π);
f (x)=2sin 2x+
3
π 2π π
(2)令2kπ− ≤2x+ ≤2kπ+ ,k∈Z,
2 3 2
7π π
解得kπ− ≤x≤kπ− ,k∈Z,
12 12
故函数 的单调递增区间为[ 7π π ], ;
f (x) kπ− ,kπ− k∈Z
12 12
因为 [ π π],所以 2π [5π 5π],则
(3) x∈ , 2x+ ∈ ,
12 2 3 6 3
当 2π 5π时,即 π 时, 取最大值,最大值为 ( π ) ,
2x+ = x= f (x) f =1
3 6 12 12
当 2π 3π时,即 5π时, 取最小值,最小值为 (5π) ,
2x+ = x= f (x) f =−2
3 2 12 12
所以f (x)的最大值为1,最小值为−2.
⃗ ⃗ 1 1 √3 1 π
19.(1)f(x)=a⋅b+ =√3sinωxcosωx−cos2ωx+ = sin2ωx− cos2ωx=sin(2ωx− ),
2 2 2 2 6
π
因为f(x)的图象上相邻两条对称轴之间的距离为 ,
2
π 2π
所以该函数的最小正周期T=2× =π,则2ω= =2,
2 T
第 页,共 页
7 1所以 ( π).
f(x)=sin 2x−
6
π π 3 π 5
(2)由 +2kπ≤2x− ≤ π+2kπ(k∈Z)得 +kπ≤x≤ π+kπ(k∈Z),
2 6 2 3 6
所以 的单调递减区间是[π 5 ] .
f(x) +kπ, π+kπ (k∈Z)
3 6
(3) 由 [f(x)] 2 −(m+1)f(x)+m=0 得 f(x)=1 或 f(x)=m ,
即 ( π) 或 ( π) ,
sin 2x− =1 sin 2x− =m
6 6
由 [ π π],可得 π [ 7π π],
x∈ − , t=2x− ∈ − ,
2 3 6 6 2
π π π
由sint=1得t=2x− = ,解得x = ;
6 2 3 3
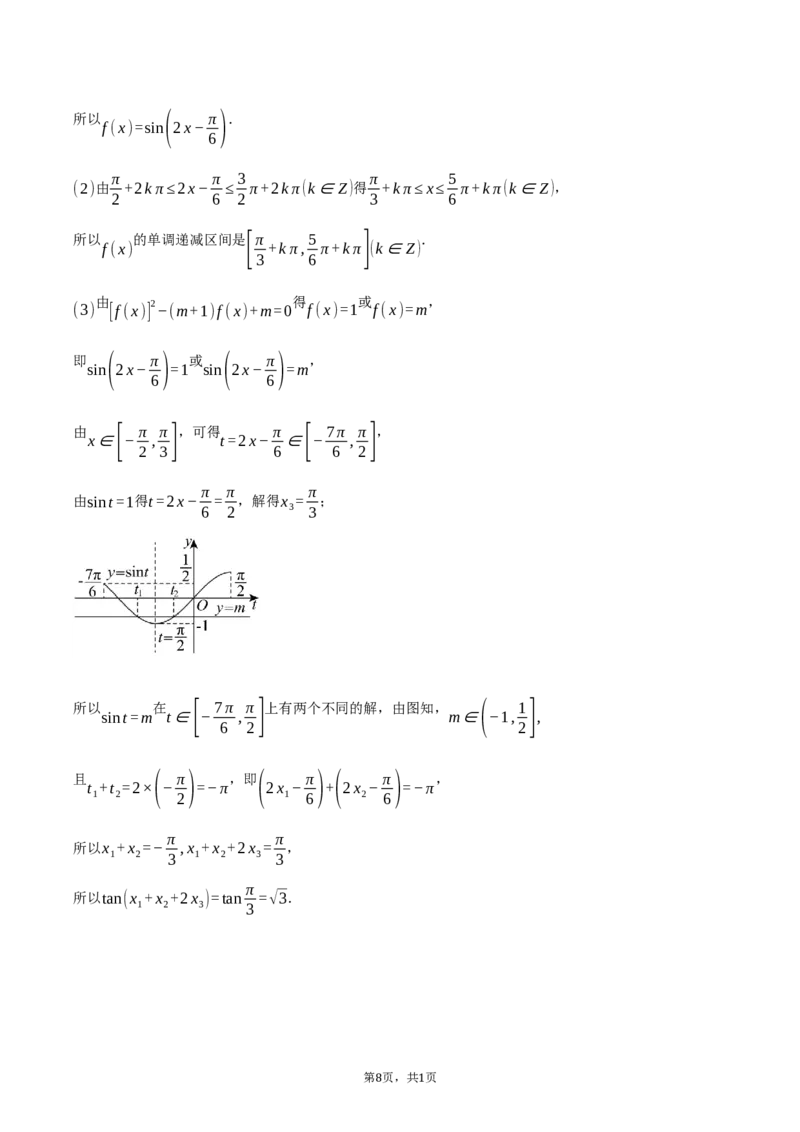
所以 在 [ 7π π]上有两个不同的解,由图知, ( 1]
sint=m t∈ − , m∈ −1, ,
6 2 2
且 ( π) ,即( π) ( π) ,
t +t =2× − =−π 2x − + 2x − =−π
1 2 2 1 6 2 6
π π
所以x +x =− ,x +x +2x = ,
1 2 3 1 2 3 3
π
所以tan(x +x +2x )=tan =√3.
1 2 3 3
第 页,共 页
8 1