数学理_2024年4月_01按日期_21号_2024届四川省绵阳市高中第三次诊断性考试_四川省绵阳市高中2021级第三次诊断性考试-理科数学

绵阳市高中 2021 级第三次诊断性考试 理科数学参考答案及评分意见 一、选择题：本大题共12小题，每小题5分，共60分． CBACB DDCBC DA 二、填空题：本大题共4小题，每小题5分，共20分． 6 13．10 14． 15．45 16．2 2 三、解答题：本大题共6小题，共70分． 100241248162 17．解：（1）由列联表可计算K2  4.7623.841，∙∙∙∙∙∙∙∙∙∙∙4分 40607228 ∴有95%的把握认为参数调试能够改变产品合格率．∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙5分 （2）根据题意，设备更新后的合格概率为0.8，淘汰品概率为0.2．∙∙∙∙∙∙∙∙∙∙∙6分 可以认为从生产线中抽出的6件产品是否合格是相互独立的，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙8分 设X表示这6件产品中淘汰品的件数，则X B(6，0.2)，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙9分 可得：pP(X 1)C00.860.20C10.850.21∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙10分 6 6 0.85(0.81.2)0.65536．∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙12分 18．解：（1）设{a }的公差为d，则1，1+d，2+2d成等比数列，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙1分 n ∴(1d)2 1(22d)，解得：d=1或d=−1，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙3分 而d=−1，不满足a ，a ，a 1成等比数列， 1 2 3 ∴d=1，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙4分 ∴数列{a }的通项公式a n．∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙5分 n n （2）令D ab a b L a b a b 3n 1，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙6分 n 1 n 2 n1 n1 2 n 1 ∴D ab a b ab L a b a b  3n11，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙7分 n1 1 n1 2 n 3 n1 n 2 n1 1 两式相减有：D D ab  (b b L b)23n， ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙8分 n1 n 1 n1 n n1 1 ∴数列{b }的前n+1项和为23n，即T 23n，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙9分 n n1 又D ab 2，所以b 2，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙10分 1 1 1 1 ∴b b L b b 23n1，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙11分 1 2 n1 n ∴T 23n1．∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙12分 n 数学（理科）评分标准 第 1 页 共 8 页19．解：（1）过C作CH⊥BB 交BB 于H，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙1分 1 1 ∵C 在平面ABB A 内的射影落在棱BB 上， 1 1 1 ∴CH 平面ABB A ，又AB平面ABB A ，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙2分 1 1 1 1 ∴CH  AB，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙3分 又ABBC，且BCI CH C，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙4分 1 1 ∴AB平面BCCB ；∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙5分 1 1 3 2 1 2 （2）∵V  S CH ，则CH  1，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙6分 ABCA 1 B 1 C 1 2 ABB 1 A 1 3 过C作CQ AA 交AA于Q，连结HQ， 1 1 ∵AA 与CC 的距离为 2 则CQ 2 ， 1 1 又∵CH 平面ABB A ，则CH HQ，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙7分 1 1 在Rt△CHQ中：HQ2 CQ2 CH2 211，则HQ1， 又AA CH 且AA CQ， 1 1 ∴AA 平面CHQ ∴AA HQ 1 1 又由（1）知：AB平面BCCB ，∴AB BB ， 1 1 1 ∴AB AA ，则四边形ABHQ为矩形， 1 ∴ABHQ1， 又四边形ABB A 的面积为3，则BB =3，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙8分 1 1 1 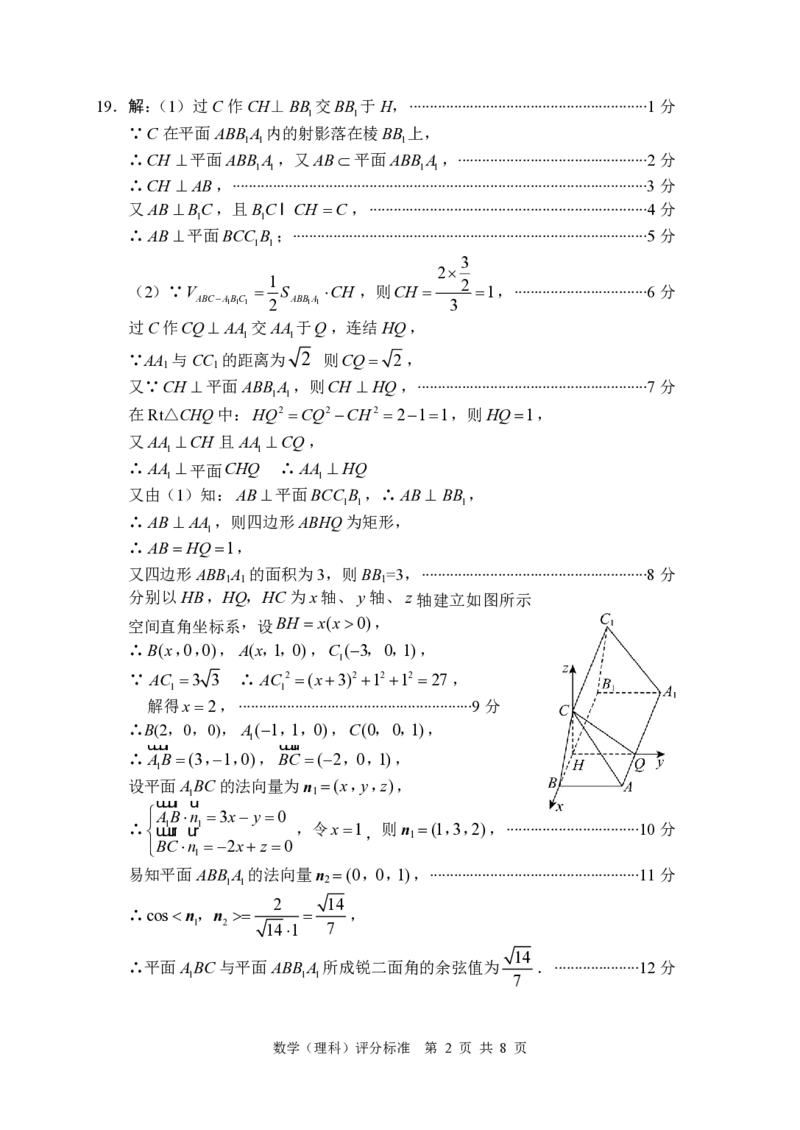分别以HB，HQ，HC为x轴、 y轴、z轴建立如图所示 空间直角坐标系，设BH x(x0)， ∴B(x，0，0)，A(x，1，0)，C (3，0，1)， 1 ∵AC 3 3 ∴AC2 (x3)2 12 12 27， 1 1 解得x2，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙9分 ∴B(2，0，0)，A(1，1，0)，C(0，0，1)， uuur 1 uuur ∴AB(3，1，0)，BC (2，0，1)， 1 设平面ABC的法向量为n (x，y，z)， 1 1 uuur ur  ABn 3x y0 ∴uu1ur ur1 ，令x1，则n 1 (1，3，2)，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙10分 BCn 2xz0 1 易知平面ABB A 的法向量n (0，0，1)，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙11分 1 1 2 2 14 ∴cosn，n   ， 1 2 141 7 14 ∴平面ABC与平面ABB A 所成锐二面角的余弦值为 ．∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙12分 1 1 1 7 数学（理科）评分标准 第 2 页 共 8 页b2 3 b 1 20．解：（1）离心率e 1  ，则  ，①∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙1分 a2 2 a 2 a2 1 a2 1 当x=1，yb ，则|AB|=2b = 3，②∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙3分 a2 a2 联立①②得: a 2，b1，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙4分 x2 故椭圆C方程为：  y2 1；∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙5分 4 （2）设过F，A，B三点的圆的圆心为Q (0，n)，A(x，y )，B(x，y )， 1 1 2 2 又F( 3，0)， 则|QA|2=|QF|2，即(x 0)2 (y n)2 (0 3)2 (n0)2，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙6分 1 1 x2 x2 又A(x ,y )在椭圆  y2 1上，故 1  y2 1， 1 1 4 4 1 带入上式化简得到：3y2 2ny 10，③∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙7分 1 1 同理，根据 QB2= QF 2可以得到：3y2 2ny 10，④ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙8分 2 2 1 由③④可得：y ,y 是方程3y2 2ny10的两个根，则y y  ，∙∙∙∙∙∙∙9分 1 2 1 2 3 x2   y2 1 设直线AB：xty1，联立方程： 4 ，  xty1 整理得：(t2 4)y2 2ty30，⑤∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙10分 3 1 故y y   ，解得：t2 5， 1 2 t2 4 3 ∴t  5，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙11分 ∴直线AB的方程为：x 5y10．∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙12分 数学（理科）评分标准 第 3 页 共 8 页1 1 21．解：（1）当a1时， f(x)( x2 x)lnx x2 x， 2 4 ∴ f(x)(x1)lnx，则切线斜率k e1，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙2分 1 ∴曲线 f(x)在(e， f(e))处的切线方程：y e2 (e1)(xe)，∙∙∙∙∙∙∙∙∙∙∙∙∙∙4分 4 3 即：(e1)x y e2 e0，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙5分 4 （2）证明方法一：因为 f(x)(xa)(lnxlna)，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙6分 由 f(x)0得到xa；由 f(x)0得到0 xa． ∴ f(x)在(0，a)单调递减，在(a，)单调递增． 5 ∴ f(x)  f(a) a2，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙7分 min 4 5 5 5 要证 f(x ) (2lna)ea1，即证： a2  (2lna)ea1， 0 8 4 8 2a2 只需证： lna20 (1a2) （*）∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙8分 ea1 2x2 设g(x) lnx2(1x2)， ex1 4x2x2 1 4x2 2x3 ex1 则g(x)   ，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙9分 ex1 x xex1 4x2 2x3 设h(x) 1(1x2)， ex1 2x310x2 8x 2x(x1)(x4) 则h(x)  ， ex1 ex1 易知：h(x)在(1，2)上单调递减， 而h(1)10，h(2)10， 故必存在唯一x (1，2)，使得h(x )0，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙10分 0 0 ∴当x(1，x )时，h(x)0，即g(x)0； 0 当x(x，2)时，h(x)0，即g(x)0， 0 ∴g(x)在(1，x )上单调递增，在(x，2)上单调递减．∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙11分 0 0 8 而g(1)0，g(2) ln220， e ∴g(x)0在(1，2)上恒成立，即（*）式成立，原命题得证．∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙12分 数学（理科）评分标准 第 4 页 共 8 页方法二：因为 f(x)(xa)(lnxlna)，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙6分 由 f(x)0得到xa；由 f(x)0得到0 xa． ∴ f(x)在(0，a)单调递减，在(a，)单调递增． 5 ∴ f(x)  f(a) a2，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙7分 min 4 5 5 5 要证 f(x ) (2lna)ea1，即证： a2  (2lna)ea1， 0 8 4 8 2a 2lna 只需证：  0(1a2)，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙8分 ea1 a 2x 2lnx 设g(x)  (1x2)，即证g(x)0在x(1，2)恒成立. ex1 x 22x 1lnx 则g(x)  (1x2)， ex1 x2 2(x2) 12lnx 令h(x)g(x)，则h(x)  (1x2)，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙9分 ex1 x3 又∵1 x2， 2(x2) 12lnx ∴ 0， 0， ex1 x3 2(x2) 12lnx ∴h(x)  0在(1，2)上恒成立.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙10分 ex1 x3 8e(1+ln2) ∴g(x)在(1，2)单调递减，又g(1)10，g(2) 0， 4e ∴存在x (1，2)，使得g(x)在(1，x )单调递增，在(x，2)单调递减. 0 0 0 8e(2ln2) 又g(1)0，g(2) 0，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙11分 2e ∴g(x)0在x(1，2)恒成立，得证．∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙12分 数学（理科）评分标准 第 5 页 共 8 页方法三：因为 f(x)(xa)(lnxlna)，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙6分 由 f(x)0得到xa；由 f(x)0得到0xa． ∴ f(x)在(0，a)单调递减，在(a，)单调递增． 5 ∴ f(x)  f(a) a2，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙7分 min 4 5 5 5 要证 f(x ) (2lna)ea1，即证： a2  (2lna)ea1， 0 8 4 8 (2lna) 只需证： ea11，(1a2)，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙8分 2a2 (2lna) 令g(a) ea1(1a2)， 2a2 a(2lna)32lna 则g(a) ea1(1a2)， 2a3 设h(a)a(2lna)32lna(1a2)，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙9分 2 ∴h'(a)3lna (1a2)，易知h(a)在(1，2)单调递增． a ∴h'(a)h'(1)10，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙10分 ∴h(a)在(1，2)单调递增， 又h(1)10，h(2)10， ∴存在唯一a (1，2)，使得当a(1，a )，h(a)0，g(a)0，g(a)单调递减， 0 0 当a(a，2)，h(a)0，g(a)0，g(a)单调递增，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙11分 0 (22ln2)e 又g(1)1，g(2) 1， 8 ∴g(a)1在a(1，2)恒成立，原不等式得证．∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙12分 数学（理科）评分标准 第 6 页 共 8 页22．（1）方法一： 3 令x0，即cos 3sin0，解得tan ，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙1分 3 5 11 ∴ 2k或 2k，kZ ，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙2分 6 6 5 1 3 当 2k时，y2  3( )4；∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙3分 6 2 2 11 1 3 当 2k时，y2  3 0，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙4分 6 2 2 ∴曲线C 与y轴的交点坐标为（0，4），（0，0）．∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙5分 1 方法二：消参：由C 的参数方程得： 1 x2 (y2)2 (cos 3sin)2 (sin 3cos)2 134，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙1分 即曲线C 的普通方程为：x2 (y2)2 4，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙2分 1 令x0，得y0或4，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙4分 ∴曲线C 与y轴的交点坐标为（0，4），（0，0）．∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙5分 1 （2）方法一：将曲线C ：x2 (y2)2 4化为极坐标方程， 1 得：4sin，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙6分   sin( )2  联立C 1 ，C 2 的极坐标方程 3 ，得4sinsin( )2， 3   4sin 1cos2 3 从而sin(sin 3cos)1  sin21，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙7分 2 2  1   5 整理得：sin(2 ) ，所以2  或 ，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙8分 6 2 6 6 6   即 或 ，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙9分 6 2    ∴∠AOB   ．∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙10分 2 6 3  方法二：将C 的极坐标方程sin( )2， 2 3 化为直角坐标方程： 3x y40，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙6分 2 ∴C 是过点（0,4）且倾斜角为 的直线，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙7分 2 3   不妨设B（0,4），则∠OBA ，因为BO为直径，所以∠BAO ， ∙∙∙∙∙∙∙∙9分 6 2    ∴∠AOB   ．∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙10分 2 6 3 数学（理科）评分标准 第 7 页 共 8 页3 3 3(ab) 23.（1）由ab  得ab ab3， ①∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙1分 a b ab 又由 f(x) xa  xb （xa)(xb)  ba 2，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙3分 且ab0，所以ab2， ②∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙4分 由①②得：a3,b1；∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙5分 （2） 3at  bt  33t  t  3 1t  t ，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙6分  令 t sin，0 ，则 1t cos，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙7分 2  ∴ 3 1t  t  3cossin2sin( )，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙9分 3  1 ∴当 时，即t  时， 3at  bt 的最大值为2．∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙10分 6 4 数学（理科）评分标准 第 8 页 共 8 页