文档内容
数学答案与解析
1.D 2.C 3.A 4.A 5.B
6.【答案】B
→ → →
【解析】由AP=λAB+μAD,当 P在直线 BD上时,λ+μ=1,当
圆C与DB的切点在DB延长线上时,圆C落在四边形ABCD内
π
部部分与直线 DB没有公共点,此时 λ+μ>1,得∠DBC> ,
2
π π
0<∠C< ,故答案为(0, ).
3 3
7.【答案】D
【解析】f(x)为偶函数,所以f(x)=f(-x),f′(x)=-f′(-x)g(x)=-g(-x),
所以g(x)为奇函数.
3 3 3 3 3
g(0)=0.因为f( -2x)为奇函数,所以f( -2x)=-f( +2x),得f( -x)=-f( +x),
4 4 4 4 4
3 3 3
即f(x)关于点( ,0)对称,所以f′( +x)=f′( -x),
4 4 4
3 3 3
即g( +x)=g( -x)g(x)=g( -x), ①
4 4 2
3 3
所以g(x)=-g(-x)=g( -x)g(x)=-g(x+ ), ②
2 2
得g(x)=g(x+3),g(x)的周期为3.
故g(x)为周期为3的奇函数.g(0)=g(3)=0.
又2是f(x)的极值点,得g(2)=0,g(5)=0,g(-2)=0,g(1)=0,g(4)=0.
g(x)=g(x+3),又g(x)为奇函数,g(x)=-g(-x)=g(x+3),得-g(-x)=g(x+3),
3 3 3 9
所以g(x)关于点( ,0)对称,故g( )=0,且g( +3)=g( )=0,
2 2 2 2
3 3 1 1 1 7
由①g(x)=g( -x)g(1)=g( -1)=g( )=0,又g( )=g( +3)=g( )=0
2 2 2 2 2 2
3 3 5 5 5 11
由②g(x)=-g(x+ )g(1)=-g(1+ )=-g( )=0,又g( )=g( +3)=g( )=0
2 2 2 2 2 2
1 3 5 7 9 11
故g(x)=0在(0,6)内解最少有 ,1, ,2, ,3, ,4, ,5, ,最少有11个.
2 2 2 2 2 2
{#{QQABIYgUggAAAJIAARgCAwWwCgIQkAGCAIoOxAAIsAIACRFABAA=}#}
书书书8.【答案】C
a n+1
【解析】由na =(2n+2)a,得 n+1=2 ,
n+1 n a n
n
a n a n-1a n-2 a 2
所以 n =2 ,n-1=2 ,n-2=2 ,…,2=2 (n≥2,n∈N)
a n-1a n-2a n-3 a 1
n-1 n-2 n-3 1
a n
n=2n-1 ,得a=n2n-1.
a 1 n
1
设S=a+a+a+…+a =1·20+2·21+3·22+4·23+…+100·299 ①
1 2 3 100
则2S=1·21+2·22+3·23+4·24+…+100·2100 ②
①-②得-S=1+2+22+23+…+299-100·2100
1-2100
-S= -2100·100=-99·2100-1
1-2
S=99·2100+1
a 100·299 50
100 = = .
a+a+a+…+a 99·2100 99
2 3 4 100
9.BD
10.【答案】ACD
x x
【解析】【法一】由槡1+cosx+槡1-cosx=槡2cos2 +槡2sin2 =槡k得
2 2
( x x )
槡2 cos + sin =槡k
2 2
( x x )2 k-2
2 cos + sin =k2+2sinx=k sinx= .
2 2 2
k-2 槡2
由y= sinx的图象可知, 的值为0,1, 时,
2 2
槡1+cosx+槡1-cosx=槡k的正根构成等差数列,得k=2,4,2+槡2,故选ACD.
x x ( x x )
【法二】y=槡1+cosx+槡1-cosx=槡2cos2 +槡2sin2 =槡2 cos + sin
2 2 2 2
其周期为π,设x∈[0,π]
( x x )
则y=槡2 cos + sin x∈[0,π],
2 2
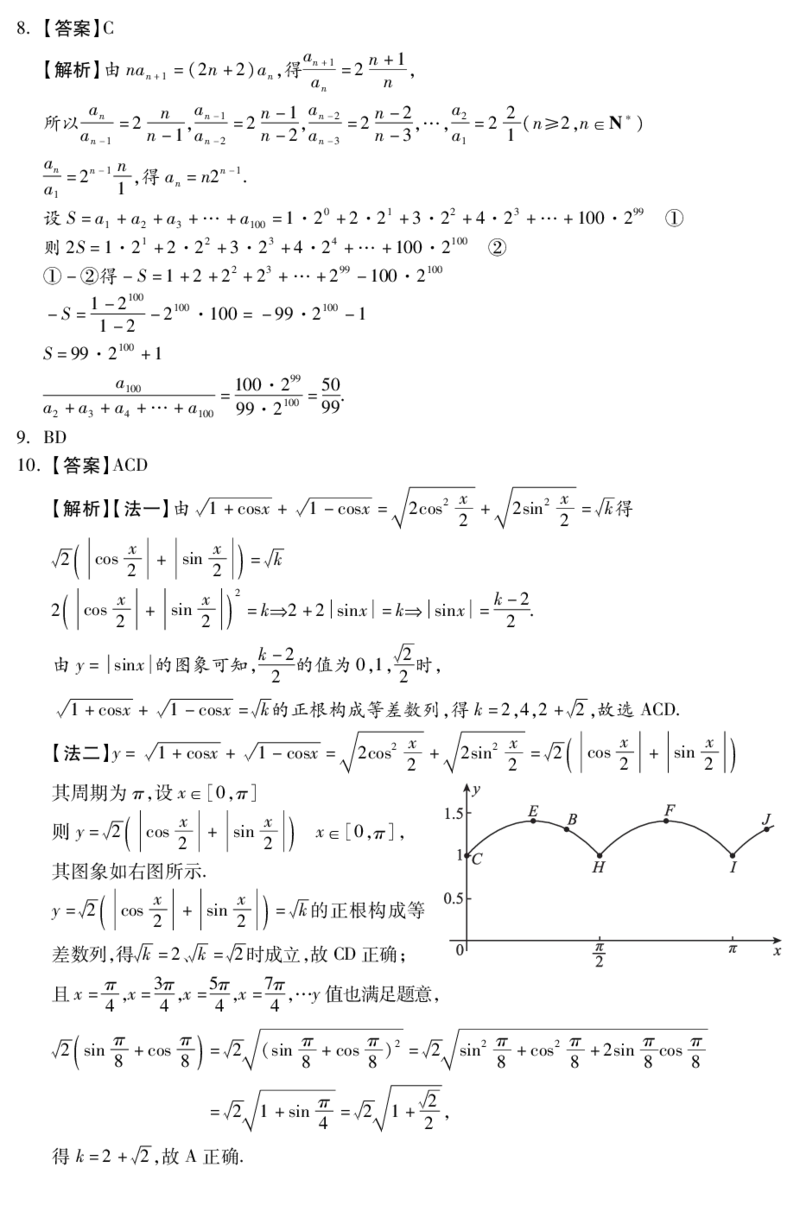
其图象如右图所示.
( x x )
y=槡2 cos + sin =槡k的正根构成等
2 2
差数列,得槡k=2、槡k=槡2时成立,故CD正确;
π 3π 5π 7π
且x= ,x= ,x= ,x= ,…y值也满足题意,
4 4 4 4
( π π) π π π π π π
槡2sin +cos =槡2槡(sin +cos )2=槡2槡sin2 +cos2 +2sin cos
8 8 8 8 8 8 8 8
π 槡2
=槡2槡1+sin =槡2槡1+ ,
4 2
得k=2+槡2,故A正确.
{#{QQABIYgUggAAAJIAARgCAwWwCgIQkAGCAIoOxAAIsAIACRFABAA=}#}11.【答案】BCD
1
【解析】f(x)= x4-bx2+cx有三个不同极值点x,x,x,
4 1 2 3
则f′(x)=x3-2bx+c=0有三个不等实根为x,x,x,则x3-2bx=-c定有三个解.
1 2 3
设g(x)=x3-2bxg′(x)=3x2-2b,
当b≤0,g′(x)=3x2+2b≥0,得g(x)单调递增,
2b
x3-2bx=-c不会有三个解,所以b>0,g′(x)=3x2-2b=0x±槡,
3
2b 2b 2b 2b
得g(x)在(-∞,-槡)单调递增,在(-槡,槡)单调递减,在(槡,+∞)单调递增.
3 3 3 3
2b
x3-2bx=-c定有三个解g(-槡)>-c恒成立,
3
2b
因为-c∈(0,1],所以g(-槡)>1恒成立.
3
3
即g(-槡
2b
)=(-槡
2b
)3+2b槡
2b
>1,得b>
3槡2
,故A错误;
3 3 3 4
设x3-2bx+c=(x-x)(x-x)(x-x)
1 2 3
=x3-(x+x+x)x2+(xx+xx+xx)x-xxx,
1 2 3 12 13 23 123
故x+x+x=0,xx+xx+xx=-2b,xxx=-c,故xxx∈(0,1],故D正确;
1 2 3 12 13 23 123 123
又(x+x+x)2=x2+x2+x2+2xx+2xx+2xx=0
1 2 3 1 2 3 12 13 23
x2+x2+x2=-(2xx+2xx+2xx)=4b>3槡 3 2,故B正确;
1 2 3 12 13 23
又x3+2bx+c=0,x3+2bx+c=0,x3+2bx+c=0,
1 1 2 2 3 3
则x3+x3+x3=-2bx-c-2bx-c-2bx-c=-3c,
1 2 3 1 2 3
又c∈[-1,0),故-3c∈(0,3],
x3+x3+x3的最大值为3,故C正确.
1 2 3
392π
12.3 13.
9
槡2(e2+1)
14.
4e2
y
【解析】由 y≤ ≤ lnx,得0<x≤1,
x
y
又 ≤ lnx,
x
当y≥0时,y≤-xlnx,
当y<0时,y≥xlnx,
由函数y=xlnx与y=-xlnx图象可知点 P位于
图中阴影部分区域,
则点P到直线x-y-m=0(m∈R)最大距离的
最小值为函数y=-xlnx上切线斜率为1的点到直线x-y-1=0的距离的一半.
{#{QQABIYgUggAAAJIAARgCAwWwCgIQkAGCAIoOxAAIsAIACRFABAA=}#}y=-xlnxy′=-lnx-1,
设-lnx-1=1,得x=e-2,
0 0
点(e-2,2e-2)到x-y-1=0的距离为
e-2-2e-2-1
=
e-2+1
=
槡2(e2+1)
.
槡2 槡2
2e2
槡2(e2+1)
故答案为 .
4e2
四、解答题:本题共5小题,共77分。解答应写出文字说明、证明过程或演算步骤。
15.解:(1)因为S=1-2-n
n
1
当n≥2时,a=S-S =1-2-n-(1-2-n+1)= !!!!!!!!!!!!!! 2分
n n n-1 2n
1
又因为n=1时,a=S=1-2-1= 也满足上式 !!!!!!!!!!!!!!! 3分
1 1 2
1
所以当n∈N时,a= !!!!!!!!!!!!!!!!!!!!!!!!! 4分
n 2n
1
b
n
=log1
2
a
n
=log1
22n
=n!!!!!!!!!!!!!!!!!!!!!!!!!! 5分
1 1 1 1
(2)由b=n,得 = = -
n bb n(n+1) n n+1
n n+1
1 1 1 1 1 1 1 1 1 1 1
T= + + +…+ = - + - +…+ - =1- !! 8分
n bb bb bb b b 1 2 2 3 n n+1 n+1
12 23 34 n-1 n
1 1 1 1 2n-(n+1)
S-T=(1- )-(1- )= - = !!!!!!!!!!! 10分
n n 2n n+1 n+1 2n (n+1)2n
当n=1时,2n=n+1
当n≥2时,2n=C0+C1+C2+…+Cn=1+n+C2+…+Cn>n+1,S>T.!!!! 12分
n n n n n n n n
综上所述:当n=1时,S=T,当n≥2时,S>T. !!!!!!!!!!!!!! 13分
n n n n
16.解:(1)等腰直角△ABC中,AB=BC,得∠ABC=90°
点E、F分别为AB,AC的中点,EF∥BC,
所以EF⊥AB.!!!!!!!!!!!!!!!!!! 2分
将△沿EF翻折到△DEF位置后,EF⊥ED,EF⊥EB,
ED面BDE,EB面BDE,DE∩EB=E,
所以EF⊥面BDE.!!!!!!!!!!!!!!!!!!!!!!!!!!!! 4分
又EF∥BC,得BC⊥面BDE,又BC面BCD,所以平面BCD⊥平面BDE !!!!! 6分
(2)【法一】由(1)知BC⊥面BDE,所以面ABC⊥面BDE.
又因为DB=EB,所以△BDE为等边三角形,
设EB的中点为O,则DO⊥面 ABC,过 O作 OM⊥AB交 AC
于M.以O为坐标原点,OM,OB,OD所在直线分别为 x,y,z
轴建立如图所示的空间直角坐标系.
不妨设AB=BC=4,
得D(0,0,槡3),E(0,-1,0),F(2,-1,0),C(4,1,0)
{#{QQABIYgUggAAAJIAARgCAwWwCgIQkAGCAIoOxAAIsAIACRFABAA=}#}→ → →
所以ED=(0,1,槡3),EF=(2,0,0),EC=(4,2,0)!!!!!!!!!!!!!!! 9分
设平面DEF的一个法向量为m=(x,y,z),
1 1 1
→
{m·ED=0 {y+槡3z=0
则 1 1
→
m·EF=0 x=0
1
可取m=(0,3,-槡3),!!!!!!!!!!!!!!!!!!!!!!!!!! 11分
设平面DEC的一个法向量为n=(x,y,z),
2 2 2
→
{n·ED=0 {y+槡3z=0
则 2 2
→
n·EC=0 4x+2y=0
2 2
3
可取n=(- ,3,-槡3),!!!!!!!!!!!!!!!!!!!!!!!!! 13分
2
m·n 12 4槡19
则cos<m,n>= = = ,
m · n 槡57 19
2槡3·
2
4槡19
平面DEF与平面DEC夹角的余弦值为 .!!!!!!!!!!!!!!!! 15分
19
【法二】点E、F分别为AB,AC的中点,EF∥BC,BC⊥面DEB,
所以EF⊥面DEB,
面DEF⊥面DEB,且面DEF∩面DEB=DE,
不妨设AB=BC=4,则点B到面DEF的距离为槡3,!!! 8分
故点C到面DEF的距离为槡3.
设EB的中点为O,则DO⊥面ABC,
∠OBC=90°,BD=4,OB=1OC=槡17,BE=2EC=2槡5 !!!!!!!!!! 10分
△DOC中∠DOC=90°,OC=槡17,OD=槡3DC=2槡5 !!!!!!!!!!!! 11分
所以△DEC为等腰三角形,DC=EC=2槡5且DE=2,得点C到DE的距离为槡19,
又C到面DEF的距离为槡3,
槡3
所以平面DEF与平面DEC夹角的正弦值为 , !!!!!!!!!!!!!! 13分
槡19
4槡19
得平面DEF与平面DEC夹角的余弦值为 .!!!!!!!!!!!!!!! 15分
19
17.解:(1)该校随机抽取三人,每个人满分的概率为40%.
设抽取的三人中满分人数为X,则X=0,1,2,3.
2 27
则P(X=0)=(1- )3= ,
5 125
2 3 54
P(X=1)=C1 ( )2= ,
35 5 125
2 3 36
P(X=2)=C2( )2 = ,
3 5 5 125
{#{QQABIYgUggAAAJIAARgCAwWwCgIQkAGCAIoOxAAIsAIACRFABAA=}#}2 8
P(X=3)=C3( )3= ,!!!!!!!!!!!!!!!!!!!!!!!!! 2分
3 5 125
则X的分布列为
X 0 1 2 3
27 54 36 8
P
125 125 125 125
2
∵X~B(3, ),
5
2 6
∴数学期望E(X)=3× = . !!!!!!!!!!!!!!!!!!!!!! 4分
5 5
(2)【法一】设该校总人数为N人,则体育项目测试满分的有 N×40% =04N人,每天运动
时间超过两个小时的人数有N×20%=02N人,!!!!!!!!!!!!!!! 5分
超过两个小时的人体育项目测试满分率约为50%,则其中测试满分的有个02N×50% =
0.1N个人,!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! 6分
因此每天运动时间不超过两个小时的学生有N×(1-20%)=08N个人中,测试满分的有
0.3N 3
0.4N-0.1N=0.3N个人,任取1名学生,他体育测试满分的概率为P= = . !!
0.8N 8
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! 9分
【法二】用A表示事件“抽到每天运动时间超过两个小时的学生”,
则P(A)=20%,P(珔A)=1-20%=80%.
用B表示事件“抽到体育项目测试满分的学生”,
则P(B)=40%,且P(B|A)=50%.
又P(AB)=P(A)P(B|A)=20%·50%=10% !!!!!!!!!!!!!!!! 6分
P(B)=P(AB)+P(珔AB)=10%+P(珔AB)=40%
故P(珔AB)=30%. !!!!!!!!!!!!!!!!!!!!!!!!!!!! 8分
P(珔AB)
30% 3
P(B|珔A)= = = .!!!!!!!!!!!!!!!!!!!!!!! 9分
P(珔A) 80% 8
(3)【法一】记A表示事件“经过n次传球后,球在乙的手中”,
n
设n次传球后球在乙手中的概率为p,n=1,2,3,…,n,
n
1 —
则有p= ,A =A·A +A·A ,!!!!!!!!!!!!!!!!!! 10分
1 2 n+1 n n+1 n n+1
—
所以p =P(A·A +A·A )
n+1 n n+1 n n+1
—
=P(A·A )+P(A·A )
n n+1 n n+1
— —
=P(A)·P(A |A)+P(A)·P(A |A)
n n+1 n n n+1 n
1
=(1-p)· +p·0
n 2 n
1
= (1-p),
2 n
{#{QQABIYgUggAAAJIAARgCAwWwCgIQkAGCAIoOxAAIsAIACRFABAA=}#}1 1
即p =- p+ ,n=1,2,3,…,!!!!!!!!!!!!!!!!!!!! 12分
n+1 2 n 2
1 1 1 1 1
所以p - =- (p- ),且p- = ,
n+1 3 2 n 3 1 3 6
{ 1} 1 1
所以数列 p- 表示以 为首项,- 为公比的等比数列,!!!!!!!!!! 14分
n 3 6 2
1 1 1
所以p- = ×(- )n-1,
n 3 6 2
1 1 1 1 1
所以p= ×(- )n-1+ = [1-(- )n].
n 6 2 3 3 2
1 1
即n次传球后球在乙手中的概率是 [1-(- )n].!!!!!!!!!!!!! 16分
3 2
【法二】记A表示事件“经过n次传球后,球在甲的手中”,
n
设n次传球后球在甲手中的概率为p,n=1,2,3,…,n,
n
—
则有p=0,A =A·A +A·A ,!!!!!!!!!!!!!!!!!!! 10分
1 n+1 n n+1 n n+1
—
所以p =P(A·A +A·A )
n+1 n n+1 n n+1
—
=P(A·A )+P(A·A )
n n+1 n n+1
— —
=P(A)·P(A |A)+P(A)·P(A |A)
n n+1 n n n+1 n
1
=(1-p)· +p·0
n 2 n
1
= (1-p),
2 n
1 1
即p =- p+ ,n=1,2,3,…,!!!!!!!!!!!!!!!!!!!! 12分
n+1 2 n 2
1 1 1 1 1
所以p - =- (p- ),且p- =- ,
n+1 3 2 n 3 1 3 3
{ 1} 1 1
所以数列 p- 表示以- 为首项,- 为公比的等比数列,
n 3 3 2
1 1 1
所以p- =(- )×(- )n-1,
n 3 3 2
1 1 1 1 1
所以p=(- )×(- )n-1+ = [1-(- )n-1]!!!!!!!!!!!! 14分
n 3 2 3 3 2
1 1
即n次传球后球在甲手中的概率是 [1-(- )n-1],因为由甲先传球,则 n次传球后球
3 2
1 1
1- [1-(- )n-1]
3 2 1 1
在乙和丙手中的概率相等为 = [1-(- )n]!!!!!! 16分
2 3 2
18.解:f(x)=(x2+ax)exf′(x)=[x2+(a+2)x+a]ex !!!!!!!!!!!!! 2分
因为ex>0,设g(x)=x2+(a+2)x+a,Δ=(a+2)2-4a=a2+4>0,
-(a+2)±槡a2+4
则g(x)=x2+(a+2)x+a=0x = !!!!!!!!!!! 4分
1,2 2
{#{QQABIYgUggAAAJIAARgCAwWwCgIQkAGCAIoOxAAIsAIACRFABAA=}#}-(a+2)-槡a2+4
当x∈(-∞, )时,g(x)>0f′(x)>0,f(x)单调递增.
2
-(a+2)-槡a2+4 -(a+2)+槡a2+4
当x∈( , )时,g(x)<0f′(x)<0,f(x)单调递减.
2 2
-(a+2)+槡a2+4
当x∈( ,+∞)时,g(x)>0f′(x)>0,f(x)单调递增.
2
-(a+2)-槡a2+4 -(a+2)+槡a2+4
综上所述:f(x)的单调递增区间为(-∞, ),( ,
2 2
-(a+2)-槡a2+4 -(a+2)+槡a2+4
+∞),单调递减区间为( , ).!!!!!!! 6分
2 2
(2)若f(x)=x即(x2+ax)ex=x只有一个解,
因为x=0使方程成立,所以只有0是f(x)=x的解.
x≠0时,(x+a)ex=1无非零解.!!!!!!!!!!!!!!!!!!!!!! 7分
设h(x)=(x+a)ex-1,则h′(x)=(x+a+1)ex,
当x<-a-1,h′(x)<0,h(x)单调递减,
当x>-a-1,h′(x)>0,h(x)单调递增,
所以h(x)最小值为h(-a-1)=-e-a-1-1<0,
当x→-∞时,h(x)→-1,当x→+∞时,h(x)→+∞,故h(x)=(x+a)ex-1定有零点,又
因为(x+a)ex=1无非零解,有零点应还是0.
所以h(0)=(0+a)e0-1=0a=1,则f(x)=(x2+x)ex,!!!!!!!!!!! 10分
f(x)
>(kx-x2)(ex-1)得x2+x>(kx-x2)(ex-1)
ex
x+1 x+1
x>0,ex>1, >k-x得k< +x
ex-1 ex-1
x+1
设F(x)= +x
ex-1
-1-xex ex(ex-x-2)
F′(x)= +1= !!!!!!!!!!!!!!!!!!!! 12分
(ex-1)2 (ex-1)2
令G(x)=ex-x-2得G′(x)=ex-1
因为x>0ex>1G′(x)>0,G(x)=ex-x-2在(0,+∞)上单调递增,
又G(1)=e-3<0,G(2)=e2-4>0,
ex0(ex0-x-2)
所以x∈(1,2)使得G(x)=0ex0=x+2,且F′(x)= 0 =0.!! 14分
0 0 0 0 (ex0-1)2
x+1
x∈(0,x)F′(x)<0,F(x)= +x单调递减,
0 ex-1
x+1
x∈(x,+∞)F′(x)>0,F(x)= +x单调递增,
0 ex-1
x+1
所以F(x)最小值F(x)= 0 +x
0 ex0-1 0
x+1
且ex0=x+2,得F(x)=0 +x=x+1!!!!!!!!!!!!!!!!! 16分
0 0 x+1 0 0
0
{#{QQABIYgUggAAAJIAARgCAwWwCgIQkAGCAIoOxAAIsAIACRFABAA=}#}x+1
又因为x∈(1,2)x+1∈(2,3),所以k< +xk<x+1,
0 0 ex-1 0
故整数k的最大值为2. !!!!!!!!!!!!!!!!!!!!!!!!! 17分
1
19.解:(1)函数y=x+ 的图象是圆锥曲线中的双曲线,
x
且y轴和直线y=x是它的渐近线可知,对称轴为直线
3π 7π
y=tan ·x和y=tan ·x.!!!!!!!!! 2分
8 8
π
2tan
π π 8 π π
tan =tan(2· )= ,得tan2 +2tan -1=0
4 8 π 8 8
1-tan2
8
π 3π π π
解得tan =槡2-1, + = ,
8 8 8 2
π 3π 3π
所以tan ·tan =1得tan =槡2+1,
8 8 8
7π π π
tan =tan(π- )=-tan =1-槡2,
8 8 8
所以对称轴l的方程为y=(槡2+1)x和y=(1-槡2)x.!!!!!!!!!!!!! 5分
(2)(ⅰ)【法一】在转轴下,设坐标轴的旋转角为 α,平面
上任一点P在旧坐标系 xOy与新坐标系 x′Oy′内的坐标
分别为(x,y)与(x′,y′),作 PM⊥Ox,PN⊥Ox′再设
∠POx′=θ,则
x′=ON=|OP|cosθ,y′=NP=|OP|sinθ,
x=OM=|OP|cos(α+θ)=|OP|(cosαcosθ-sinαsinθ)
=x′cosα-y′sinα, !!!!!!!!!!!!!!!!!!!!!!!!!!!! 8分
y=MP=|OP|sin(α+θ)=|OP|(sinαcosθ+cosαsinθ)=x′sinα+y′cosα
3π 1
由(1)可知将坐标轴逆时针旋转 ,函数y=x+ 将变为双曲线标准方程,由公式可得
8 x
{x=x′cos
3π
-y′sin
3π x=x′
1
-y′
槡2+1
x=
1
[x′-(槡2+1)y′]
8 8 槡4+2槡2 槡4+2槡2 槡4+2槡2
y=x′sin
3π
+y′cos
3π
y=x′
槡2+1
+y′
1
y=
1
[(槡2+1)x′+y′]
8 8
槡4+2槡2 槡4+2槡2 槡4+2槡2
1 x2 y2
代入y=x+ 整理得 - =1.!!!!!!!!!!!!!!!!! 11分
x 2槡2+2 2槡2-2
3π 3π
{x=x′cos -y′sin
8 8 1
【或将 代入y=x+ ,
3π 3π x
y=x′sin +y′cos
8 8
3π 3π 3π 3π 1
得x′sin +y′cos =x′cos -y′sin +
8 8 8 8 3π 3π
x′cos -y′sin
8 8
3π 3π 3π 3π 3π 3π
(x′sin +y′cos -x′cos +y′sin )(x′cos -y′sin )=1
8 8 8 8 8 8
{#{QQABIYgUggAAAJIAARgCAwWwCgIQkAGCAIoOxAAIsAIACRFABAA=}#}3π 3π 3π 3π 3π 3π
[x′(sin -cos )+y′(cos +sin )](x′cos -y′sin )=1
8 8 8 8 8 8
3π π 3π π 3π 3π
[槡2x′sin( - )+槡2y′sin( + )](x′cos -y′sin )=1
8 4 8 4 8 8
π 5π π 5π
[槡2x′sin +槡2y′sin ][x′sin -y′sin ]=1
8 8 8 8
π 5π
槡2[x′2sin2 -y′2sin2 ]=1
8 8
π π
1-cos 1+cos
4 4
槡2[x′2 -y′2 ]=1
2 2
x2 y2
得 - =1】!!!!!!!!!!!!!!!!!!!!!!!!! 11分
2槡2+2 2槡2-2
1 3π
【法二】考虑将函数y=x+ 顺时针转 ,可得双曲线标准方程C.
x 8
任取C上一点(x,y),x=rcosθ,y=rsinθ,
3π 3π 1
则点(rcos(θ+ ),rsin(θ+ ))在y=x+ 上.
8 8 x
3π 3π 1
即rsin(θ+ )=rcos(θ+ )+ !!!!!!!!!!!!!!!! 8分
8 8 3π
rcos(θ+ )
8
3π 3π 3π
(rsin(θ+ )-rcos(θ+ ))rcos(θ+ )=1
8 8 8
3π 3π 3π 3π
r2sin(θ+ )cos(θ+ )-r2cos(θ+ )cos(θ+ )=1
8 8 8 8
r2 3π 3π
sin(2θ+ )-r2cos2(θ+ )=1
2 4 8
r2 3π 3π
[sin(2θ+ )-cos(2θ+ )-1]=1
2 4 4
r2 π r2 1
[槡2sin(2θ+ )-1]=1 [槡2cos2θ-1]=1 [r2 槡2cos2θ-r2]=1
2 2 2 2
1 1
[槡2r2cos2θ-槡2r2sin2θ-r2]=1 [槡2x2-槡2y2-x2-y2]=1
2 2
x2 y2
得 - =1 !!!!!!!!!!!!!!!!!!!!!!!!! 11分
2槡2+2 2槡2-2
x2 y2
(ⅱ)由题意知A、B为双曲线 - =1的两个焦点
2槡2+2 2槡2-2
AB2
所以 =2槡2+2+2槡2-2=4槡2!!!!!!!!!!!!!!!!!!!! 13分
2
又因为△PAB为直角三角形,所以 PA2+ PB2= AB2=16槡2
由双曲线性质可知 PA - PB =2槡2槡2+2!!!!!!!!!!!!!!! 14分
得 PA2+ PB2-2PA PB =8槡2+8
所以2PA PB =8槡2-8!!!!!!!!!!!!!!!!!!!!!!!! 16分
PA PB
得△PAB的面积为 =2槡2-2 !!!!!!!!!!!!!!!!!! 17分
2
(其他方法可酌情给分)
{#{QQABIYgUggAAAJIAARgCAwWwCgIQkAGCAIoOxAAIsAIACRFABAA=}#}