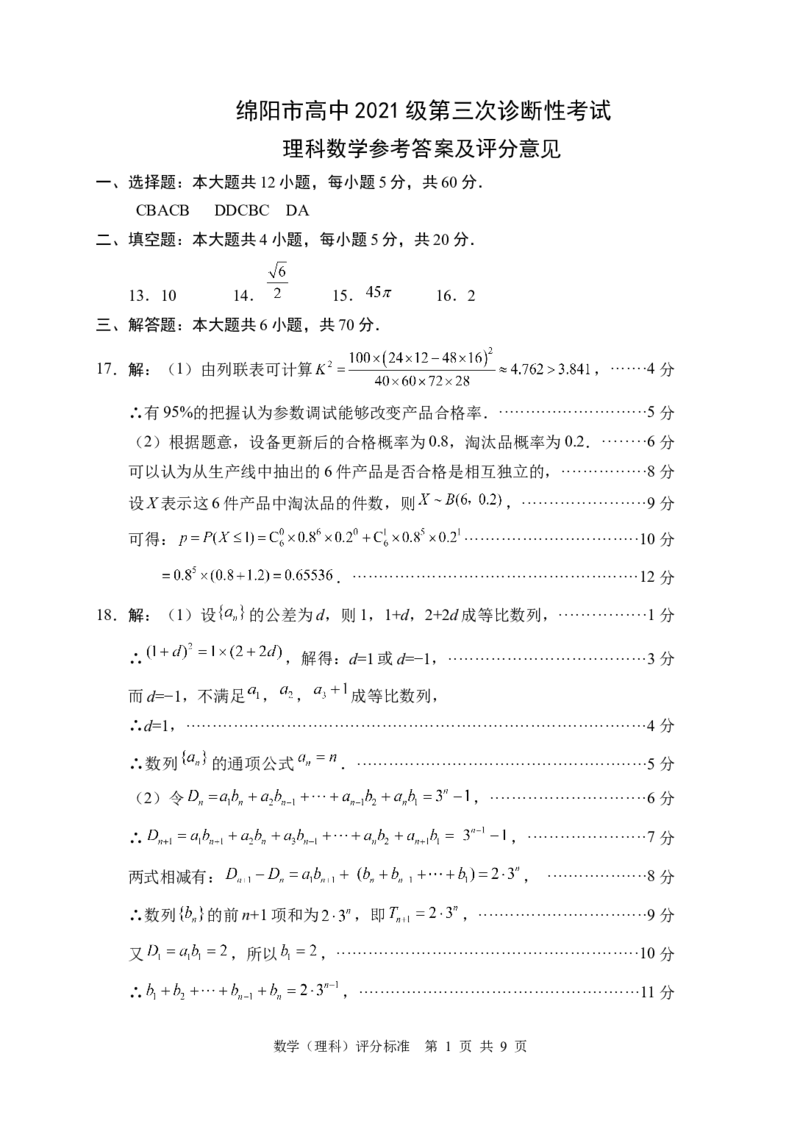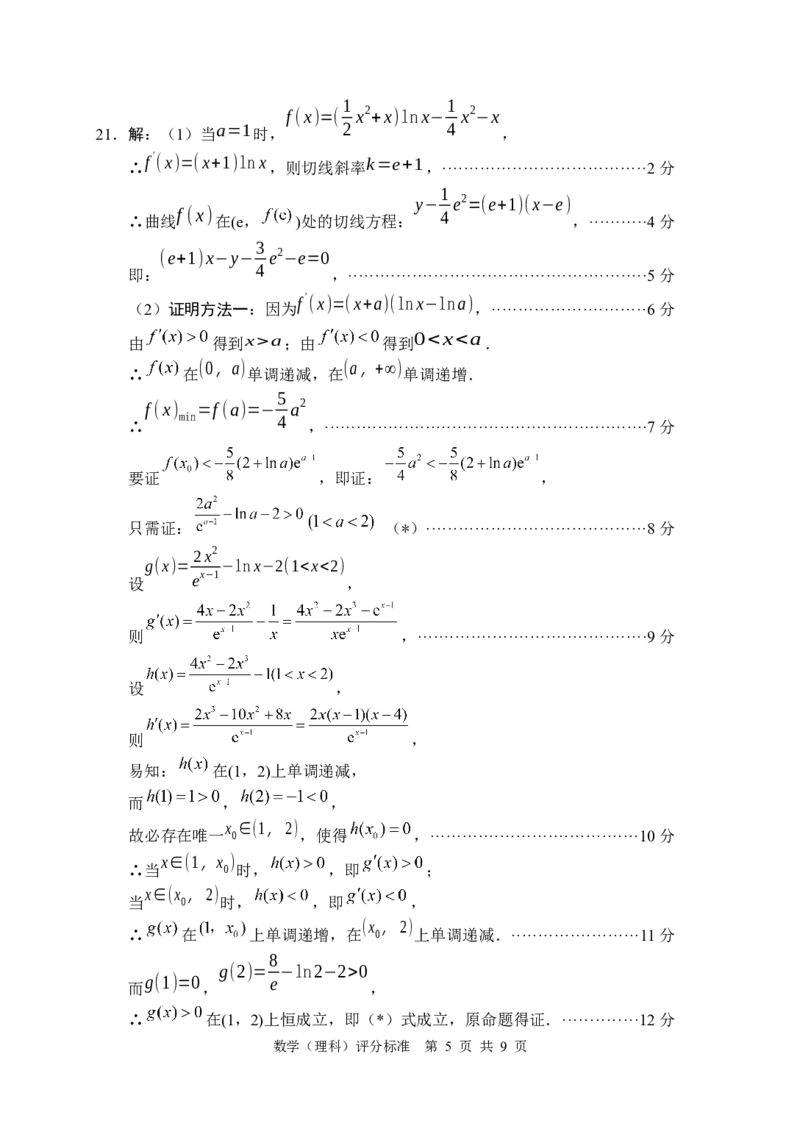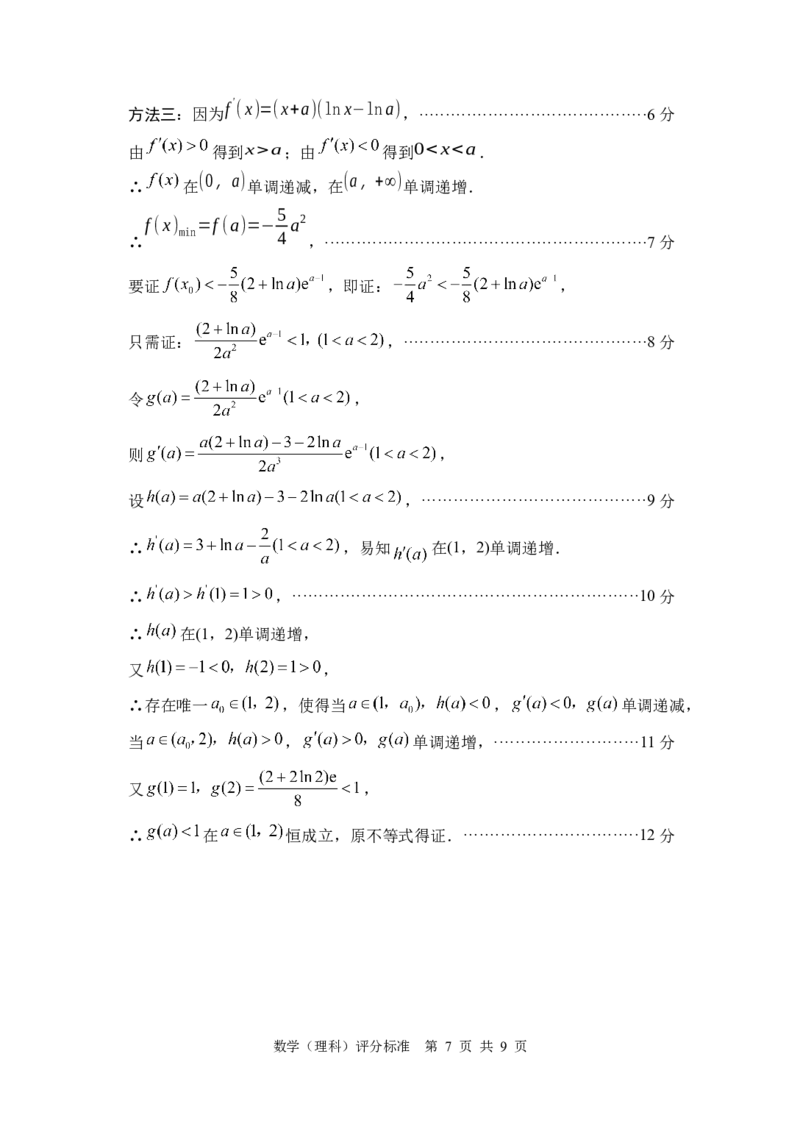数学理_2024年4月_024月合集_2024届四川省绵阳市高中第三次诊断性考试_四川省绵阳市高中2021级第三次诊断性考试-理科数学

绵阳市高中2021级第三次诊断性考试 理科数学参考答案及评分意见 一、选择题：本大题共12小题，每小题5分，共60分． CBACB DDCBC DA 二、填空题：本大题共4小题，每小题5分，共20分． 13．10 14． 15． 16．2 三、解答题：本大题共6小题，共70分． 17．解：（1）由列联表可计算 ，·······4分 ∴有95%的把握认为参数调试能够改变产品合格率．····························5分 （2）根据题意，设备更新后的合格概率为0.8，淘汰品概率为0.2．········6分 可以认为从生产线中抽出的6件产品是否合格是相互独立的，················8分 设X表示这6件产品中淘汰品的件数，则 ，·······················9分 可得： ·································10分 ．······················································12分 18．解：（1）设 的公差为d，则1，1+d，2+2d成等比数列，················1分 ∴ ，解得：d=1或d=−1，·····································3分 而d=−1，不满足 ， ， 成等比数列， ∴d=1，·······················································································4分 ∴数列 的通项公式 ．·······················································5分 （2）令 ，·····························6分 ∴ ，······················7分 两式相减有： ， ···················8分 ∴数列 的前n+1项和为 ，即 ，································9分 又 ，所以 ，·························································10分 ∴ ，·····················································11分 数学（理科）评分标准 第 1 页 共 9 页∴ ．············································································12分 19．解：（1）过C作CH⊥ 交 于H，············································1分 ∵ 在平面 内的射影落在棱 上， ∴ 平面 ，又 平面 ，···································2分 ∴ ，··············································································3分 又 ，且 ，·····················································4分 ∴ 平面 ；···································································5分 2）∵ ，则 ，·························6分 （ 过C作 交 于 ，连结 ， AA 与CC 的距离为 则 ， ∵ 1 1 平面 ，则 ，···········································7分 又∵ Rt△CHQ中： ，则 ， 在 且 ， 又 ∴ 平面 ∴ （1）知： 平面 ，∴ ， 又由 ，则四边形ABHQ为矩形， ∴ ∴ ， ABBA 的面积为3，则BB=3，············································8分 又四边形 1 1 1 分别以 为 轴、 轴、 轴建立如图所示 空间直角坐标系，设 ， ， ， ， ∴ ∴ ， ∵ 解得 ，············································9分 B(2，0，0)， ， ， ∴ ， ， ∴ 的法向量为n ， 设平面 1 数学（理科）评分标准 第 2 页 共 9 页∴ ，令 ， 则n 1 ，·························10分 的法向量n ，········································11分 易知平面 2 ， ∴ ∴平面 与平面 所成锐二面角的余弦值为 ．················12分 20．解：（1）离心率 ，则 ，①·······························1分 当x=1， ，则 ，②····························3分 联立①②得: ，···························································4分 故椭圆C方程为： ；·······················································5分 （2）设过F，A，B三点的圆的圆心为Q (0，n)， ， 又 ， 则 ，即 ，·················6分 又 在椭圆 上，故 ， 带入上式化简得到： ，③··········································7分 同理，根据 可以得到： ，④ ···················8分 由③④可得： 是方程 的两个根，则 ，·····9分 设直线AB： ，联立方程： ， 整理得： ，⑤·················································10分 数学（理科）评分标准 第 3 页 共 9 页故 ，解得： ， ∴ ，···············································································11分 ∴直线AB的方程为： ．············································12分 数学（理科）评分标准 第 4 页 共 9 页1 1 f(x)=( x2 +x)lnx− x2 −x 21．解：（1）当a=1时， 2 4 ， ∴ f' (x)=(x+1)lnx ，则切线斜率k=e+1，······································2分 1 y− e2 =(e+1)(x−e) f(x) 4 ∴曲线 在(e， )处的切线方程： ，···········4分 3 (e+1)x−y− e2 −e=0 4 即： ，························································5分 （2）证明方法一：因为 f' (x)=(x+a)(lnx−lna)，·····························6分 由 得到x>a；由 得到 00 g(1)=0 e 而 ， ， ∴ 在(1，2)上恒成立，即（*）式成立，原命题得证．··············12分 数学（理科）评分标准 第 5 页 共 9 页方法二：因为 f' (x)=(x+a)(lnx−lna)，···········································6分 由 得到x>a；由 得到 0a；由 得到0b>0，所以a−b=2， ②·······················································4分 由①②得： a=3,b=1 ；··································································5分 √3−at+√bt=√3−3t+√t=√3√1−t+√t （2） ，·································6分 π √t=sinθ，0≤θ≤ 2 √1−t=cosθ 令 ，则 ，········································7分 π √3√1−t+√t=√3cosθ+sinθ=2sin(θ+ ) ∴ 3 ，··································9分 π 1 θ= t= ∴当 6 时，即 4 时， √3−at+√bt 的最大值为2．·····················10分 数学（理科）评分标准 第 9 页 共 9 页