文档内容
新疆维吾尔自治区 2024 年普通高考第一次适应性检测
数学参考答案
一、选择题:本大题共 小题,每小题 分,共 分
8 5 40 .
1.D 2.A 3.C 4.C
5.B 6.D 7.B 8.D
二、选择题:本题共 小题,每小题 分,共 分 在每小题给出的选项中,有多项符合题目要
3 6 18 .
求 全部选对的得 分,部分选对的得部分分,有选错的得 分
. 6 0 .
9.BD 10.ABC 11.BD
三、填空题:本大题共 小题,每小题 分,共 分
3 5 15 .
1
12. 7 13. 14.-2
2
四、解答题:本大题共 小题,共 分 解答应写出文字说明、证明过程或演算步骤
5 77 . .
.解 由已知得 数列 b 的首项b b a 1
15 :(1) , { n} 1=16, 5= 2=16× =1,
16
设数列 b 的公比为q q
{ n} 1( 1>0),
b b q4
则 5 1 1 q4 1 即q 1
b = b = 1= , 1= ,
1 1 16 2
故b
n=
b
1
q
1
n -1
=16×(
1
)
n -1
=2
5- n.
………………………………………………… 6
分
2
(2) T n= b 1· b 2· b 3·…· b n=2 4 ×2 3 ×…×2 5- n =2 4+3+2+…+(5- n )
n n
4 n - ( 2 -1) - 2 1n2+ 2 9n - 2 1 ( n - 2 9 )2+ 8 8 1
=2 =2 =2 ,
即当n =4 或 5 时 , T n 有最大值 2 - 2 1 ×(4- 2 9 )2+ 8 8 1 =2 10 =1024 . ……………………… 13 分
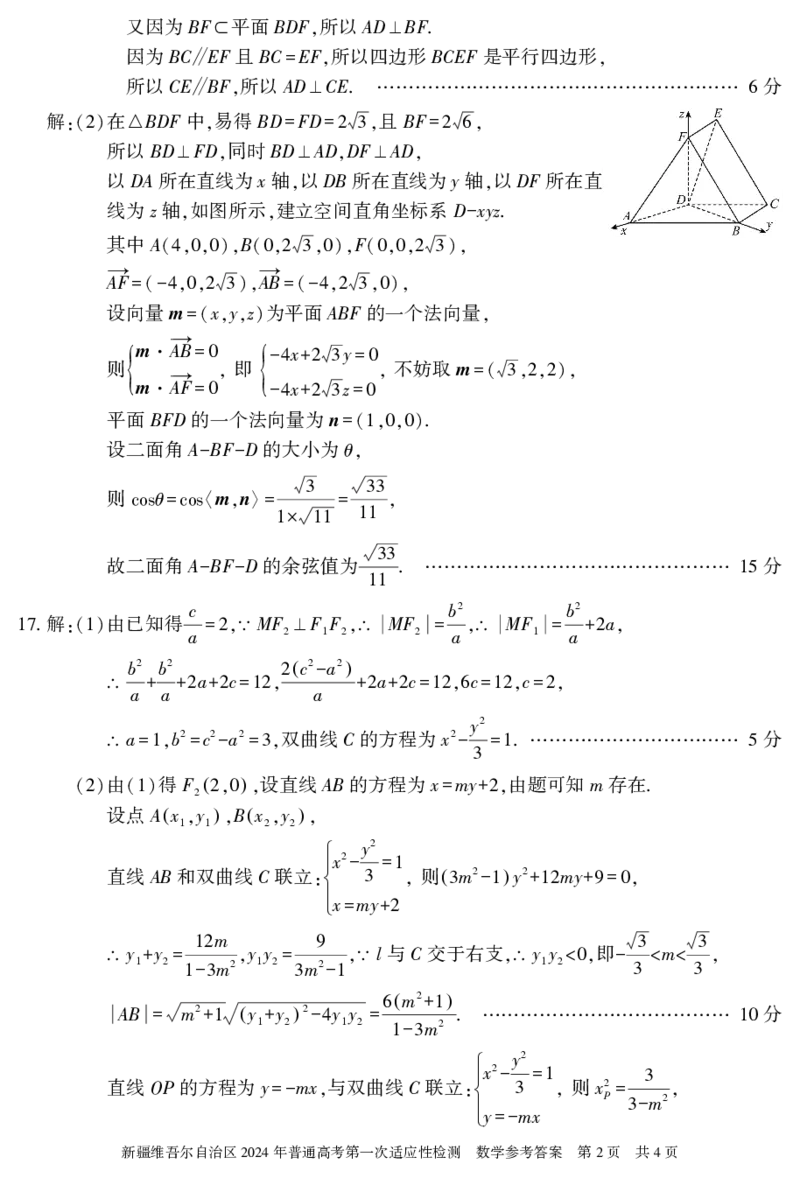
.证明 连接BD DF 在 BCD中 DC BC BCD π
16 :(1) , , △ , =4, =2,∠ = ,
3
则BD2 BC2 DC2 BC DC π
= + -2 · ·cos =12,
3
可得DC2 BC2 BD2 即BD BC
= + , ⊥ ,
由AD BC 可得BD AD 同理可得DF AD
∥ , ⊥ , ⊥ ,
因为BD AD DF AD 且BD 平面BDF DF 平面BDF BD DF D
⊥ , ⊥ , ⊂ , ⊂ , ∩ = ,
所以AD 平面BDF.
⊥
新疆维吾尔自治区 年普通高考第一次适应性检测 数学参考答案 第 页 共 页
2024 1 4
{#{QQABAYaQggCAAhAAAAhCUwVYCEMQkBGAAKoOwAAIoAABCQFABAA=}#}又因为BF 平面BDF 所以AD BF.
⊂ , ⊥
因为BC EF且BC EF 所以四边形BCEF是平行四边形
∥ = , ,
所以CE BF 所以AD CE. 分
∥ , ⊥ ………………………………………………… 6
解 在 BDF中 易得BD FD 且BF
:(2) △ , = =2 3, =2 6,
所以BD FD 同时BD AD DF AD
⊥ , ⊥ , ⊥ ,
以DA所在直线为x轴 以DB所在直线为y轴 以DF所在直
, ,
线为z轴 如图所示 建立空间直角坐标系D xyz.
, , -
其中A B F
(4,0,0), (0,2 3,0), (0,0,2 3),
A→F A→B
=(-4,0,2 3), =(-4,2 3,0),
设向量m x y z 为平面ABF的一个法向量
=( , , ) ,
{m A→B { x y
则 · =0 即 -4 +2 3 =0 不妨取m
m A→F , x z , =( 3,2,2),
· =0 -4 +2 3 =0
平面BFD的一个法向量为n .
=(1,0,0)
设二面角A BF D的大小为θ
- - ,
则 θ m n 3 33
cos =cos〈 , 〉= = ,
1× 11 11
故二面角A BF D的余弦值为 33. 分
- - ………………………………………… 15
11
c b2 b2
.解 由已知得 MF F F MF MF a
17 :(1) a =2,∵ 2⊥ 1 2,∴ 2 = a,∴ 1 = a +2 ,
b2 b2 (c2 a2 )
a c 2 - a c c c
∴ a +a +2 +2 =12, a +2 +2 =12,6 =12, =2,
y2
a b2 c2 a2 双曲线C的方程为x2 . 分
∴ =1, = - =3, - =1 …………………………… 5
3
由 得F ( ) 设直线AB的方程为x my 由题可知m存在.
(2) (1) 2 2,0 , = +2,
设点A(x y ) B(x y )
1, 1 , 2, 2 ,
ì
ï
y2
ïx2
直线AB和双曲线C联立 í - =1 则( m2 )y2 my
:ïï 3 , 3 -1 +12 +9=0,
îx my
= +2
m
y y 12 y y 9 l与C交于右支 y y 即 3 m 3
∴ 1+ 2= m2 , 1 2= m2 ,∵ ,∴ 1 2<0, - < < ,
1-3 3 -1 3 3
(m2 )
AB m2 (y y ) 2 y y 6 +1 . 分
= +1 1+ 2 -4 1 2 = m2 ………………………………… 10
1-3
ì
ï
y2
ïx2
直线OP的方程为y
=-
mx
,
与双曲线C联立
:
í
ïï
-
3
=1
,
则x2P= 3
m2 ,
îy mx 3-
=-
新疆维吾尔自治区 年普通高考第一次适应性检测 数学参考答案 第 页 共 页
2024 2 4
{#{QQABAYaQggCAAhAAAAhCUwVYCEMQkBGAAKoOwAAIoAABCQFABAA=}#}m2 m2
∴
y2P= 3
m2 , ∴ |
OP
|
2
=
x2P+ y2P= 3(
m
+
2
1)
,
3- 3-
m2 m2 m2 m2 m2
于是 1 2 3- 2-6 6-2 -2+6 4( +1) 2 为定值.
OP 2 - AB = m2 - m2 = m2 = m2 = ,
3( +1) 6( +1) 6( +1) 6( +1) 3
分
………………………………………………………………………………… 15
.
.解 由已知得 . . . μ σ 则P X . 1-0 68 . .
18 :(1) 9 39=8 57+0 82= + , ( >9 39)= =0 16
2
( )
又随机变量Y服从二项分布Y B 4
~ 2, ,
25
( ) ( )
1 1
故P Y C1 4 21 168 或 . . 分
( =1)= 2 = ( 0 2688) ………………………………… 7
25 25 625
y
由t . x . 且u 列出年份编号x和人均生产总值u的对应关系表
(2) =0 2 +2 2, = t , :
年份编号x
1 2 3 4 5
地区生产总值y 百亿元 . . . . .
( ) 14 64 17 42 20 72 25 20 30 08
地区人口总数t 百万人 . . . . .
( ) 2 4 2 6 2 8 3 0 3 2
人均生产总值u 万元 . . . . .
( ) 6 1 6 7 7 4 8 4 9 4
. . . . .
则 -x 1+2+3+4+5 -u 6 1+6 7+7 4+8 4+9 4 .
= =3, = =7 6,
5 5
n
x x u u
b ^
∑i
=1
( i- - )( i- - ) (
-2
)
×
(
-1
.
5
)
+
(
-1
)
×
(
-0
.
9
)
+0+1×0
.
8+2×1
.
8 .
= n = =0 83,
∑i ( x i- - x ) 2 4+1+0+1+4
=1
于是a u bx . . . 故u . x . . 分
^= - - ^- =7 6-0 83×3=5 11, ^=0 83 +5 11 ……………………… 17
.解 F x x 1x2 a x 易知F x 定义域为( )
19 :(1) ( )= - - ln , ( ) 0,+∞ ,
2
a x2 x a
F′ x x - +
( )= 1- - x =- x ,
当 a 即a 1 时 F′ x F x 在区间( )上单调递减
1-4 ≤0, ≥ , ( )≤0,∴ ( ) 0,+∞ ;
4
a a
当 a 即 a 1时 令F′ x x 1- 1-4 x 1+ 1-4
1-4 >0, 0< < , ( )= 0⇒ 1= , 2= ,
4 2 2
令F′ x 解得x x x 令F′ x 解得 x x 或x x .
( )>0, 1< < 2; ( )<0, 0< < 1 > 2
( ) ( )
a a a
F x 在区间 1- 1-4 上单调递减 在区间 1- 1-4 1+ 1-4 上单调递
∴ ( ) 0, , ,
2 2 2
( )
a
增 在区间 1+ 1-4 上单调递减. 分
, ,+∞ ……………………………………… 6
2
新疆维吾尔自治区 年普通高考第一次适应性检测 数学参考答案 第 页 共 页
2024 3 4
{#{QQABAYaQggCAAhAAAAhCUwVYCEMQkBGAAKoOwAAIoAABCQFABAA=}#}解法一
(2) :
由 知 a 1 x x x x a 且易知 x 1 x .
(1) ,0< < , 1+ 2=1, 1 2= , 0< 1< < 2<1
4 2
则 f x f x x 1x2 x 1x2 x x 1 x x x x
( 1)- ( 2)= 1- 1- 2+ 2= 1- 2- ( 1- 2)( 1+ 2)
2 2 2
1 x x a 1 1
= ( 1- 2)= ( x - x ),
2 2 2 2 1
又g x a g x a a (x a) a (x a)
( 1+ )- ( 2+ )= ln 1+ - ln 2+
( )
1
(x x x ) x +1 é ( ) ( )ù
a 1+ 1 2 a 2 aê ê 1 1 ú ú 分
= ln x x x = ln = ëln x +1 -ln x +1 û,……………………… 11
2+ 1 2 1 2 1
x +1
1
设1 t 1 t 则 t t .
x = 1,x = 2, 1< 2<2< 1
1 2
于是f x f x g x a g x a 等价于
( 1)- ( 2)< ( 1+ )- ( 2+ )
( ) é ( ) ( )ù
a 1 1 aê ê 1 1 ú ú
x - x < ëln x +1 -ln x +1 û,
2 2 2 1 2 1
( ) ( )
即 1 1 1 1 等价于 (t ) 1t t 1t .
ln x +1 - x < ln x +1 - x , ln 1+1 - 1< ln( 2+1)- 2
1 2 1 2 2 2 2 2
令h t t 1t t h′ t 1 1 h t 在区间 上单调递减
( )=ln( +1)- ( >1), ( )=t - <0,∴ ( ) (1,+∞) ,
2 +1 2
t t h t h t 即f x f x g x a g x a 成立. 分
∵ 1> 2,∴ ( 1)< ( 2), ( 1)- ( 2)< ( 1+ )- ( 2+ ) …… 17
解法二
:
由 知 a 1 x 1 x
(1) ,0< < ,0< 1< < 2<1,
4 2
设G x f x g x a x 1x2 a x a x a
( )= ( )- ( + )= - - ln( + )( >- ),
2
a x x a
则G′ x x - ( + -1) x a
( )= 1- -x a= x a ( >- ),
+ +
当x a 时 G′ x 故G x 在 a 上单调递增.
∈(0,1- ) , ( )>0, ( ) (0,1- )
设d x x2 x a 则x x 是d x 的两个零点.
( )= - + , 1, 2 ( )
a 1 3 a
∵ 0< < ,∴ <1- <1,
4 4
d a a 2 a a a2
∵ (1- )=(1- ) -(1- )+ = >0,
x x a G x G x
∴ 0< 1< 2<1- ,∴ ( 1)< ( 2),
即f x g x a f x g x a f x f x g x a g x a 命题得证.
( 1)- ( 1+ )< ( 2)- ( 2+ ),∴ ( 1)- ( 2)< ( 1+ )- ( 2+ ),
分
…………………………………………………………………………………… 17
以上解法仅供参考,如有其他方法,酌情给分
.
新疆维吾尔自治区 年普通高考第一次适应性检测 数学参考答案 第 页 共 页
2024 4 4
{#{QQABAYaQggCAAhAAAAhCUwVYCEMQkBGAAKoOwAAIoAABCQFABAA=}#}