数学答案_2024年2月_01每日更新_16号_2023届重庆缙云教育联盟高三3月质检各科试题及答案全科_2023届重庆缙云教育联盟高三3月质检数学

★秘密·2023年3月16日16：00前
重庆市 2022-2023 学年（下）3 月月度质量检测
高三数学答案及评分标准
2023.3
【命题单位：重庆缙云教育联盟】
1．C 2．A 3．C 4．D
5．A 6．D
π t 1t
7．D【详解】令t sin2x,x(0, ) ，则t(0,1) ，故函数g(t) ,t(0,1) ，g(t) 0 ， 即
2 et et
t π π π π
g(t) ,t(0,1)为单调增函数，而t sin2x,x(0, )在(0, ) 上递增，在( , ) 上递减，故
et 2 4 4 2
sin2x π π π π π π π π
f x 0 x 在(0, )上递增，在( , ) 上递减，又ycos(x )在(0, )上递增，在( , ) 上
esin2x  2 4 4 2 4 4 4 2
sin2x π π  π  
递减，且 f x 0 x 是正值，ycos(x ) 0 x 也是正值，故y f xcosx 在
esin2x  2 4  2  4
π π π   π π π
(0, )上递增，在( , ) 上递减，即球O的半径 f xcosx 在(0, )上递增，在( , ) 上递减，故A，
4 4 2  4 4 4 2
π
B错误；由以上分析可知当x π 时，球O的半径 f xcos  x  取到最大值为 sin 2 cos0 1 ，故球O的
4  4 sin π e
e 2
1 4π 4π 1 4π
表面积最大值为4π  ，无最小值，故C错误；同时球O的体积最大值为   ，故D正确；
e2 e2 3 e3 3e3
故选：D
8．D【详解】解:由题因为1.8220.1 ,不妨设 f xex x1,当x0时, fxex10,所以 f x 单
调递减,当x0时, fxex10, f x 单调递增,所以 f x f 00,所以
f 0.1e0.110.1 f 00,即e0.1 10.10.9 ,故2e0.1 1.8;因为
f 0.1e0.10.11e0.11.1 f 00,即e0.1 1.1,两边同时取对数有0.1ln1.1,即20.12ln1.1,即
0.2ln1.21,所以2ln1.211.8;因为1.811(10.1)2,不妨设gx2ex 1(1x)2,则
gx2ex 2x22f x2f 00,所以gx 单调递增,所以g0.12e0.11(10.1)2  g00,故
2e0.11.81;因为1.811(10.1)2,不妨设hx1(1x)222ln1x x22x2ln1x
,则
高三数学答案 第 1 页 共 6 页
学科网（北京）股份有限公司hx
2x2
0,所以hx 单调递增,所以h0.11.8122ln1.1h00,故1.812ln1.21.综
1x
上,a1.8,1.81,b1.8,1.81
.故选:D
9．BC 10．CD
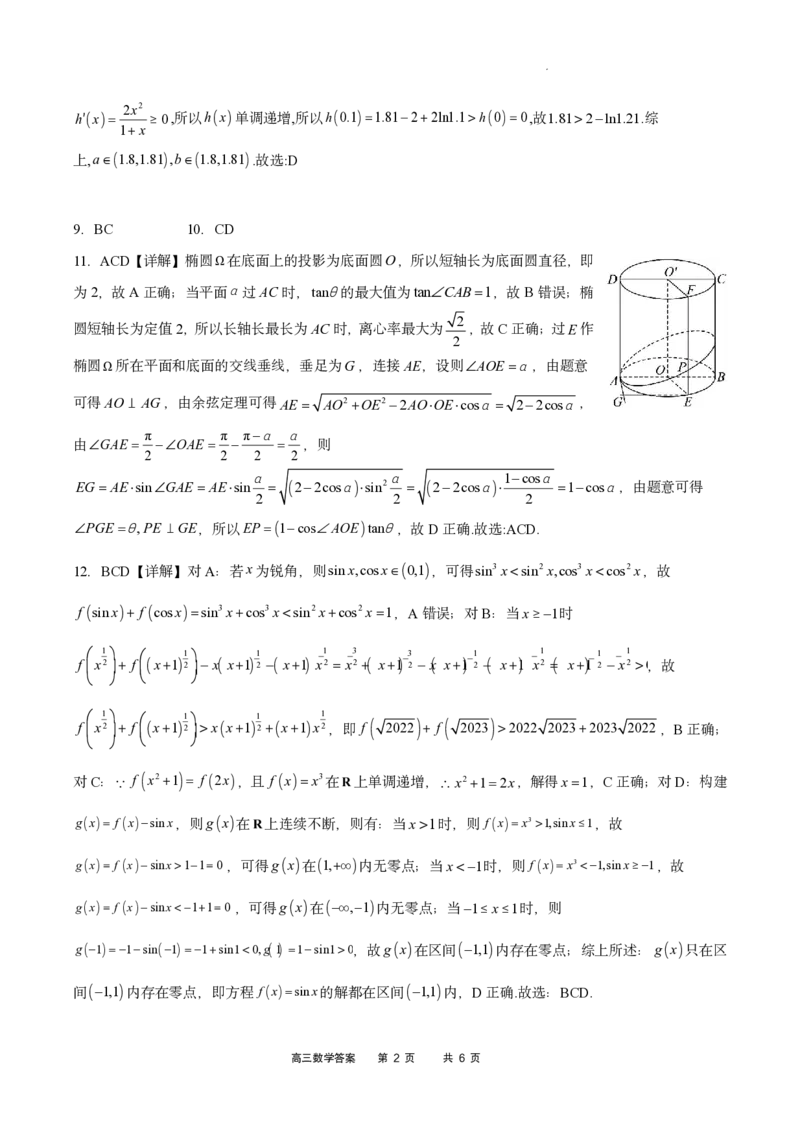
11．ACD【详解】椭圆Ω在底面上的投影为底面圆O，所以短轴长为底面圆直径，即
为2，故A正确；当平面过AC时，tan的最大值为tanCAB1，故B错误；椭
2
圆短轴长为定值2，所以长轴长最长为AC时，离心率最大为 ，故C正确；过E作
2
椭圆Ω所在平面和底面的交线垂线，垂足为G，连接AE，设则AOE，由题意
可得AO AG，由余弦定理可得AE AO2OE22AOOEcos 22cos，
π π π 
由GAE  OAE    ，则
2 2 2 2
  1cos
EG AEsinGAE AEsin  22cossin2  22cos 1cos，由题意可得
2 2 2
PGE ,PE GE，所以EP1cosAOEtan，故D正确.故选:ACD.
12．BCD【详解】对A：若x为锐角，则sinx,cosx0,1 ，可得sin3xsin2x,cos3xcos2x，故
f sinx f cosxsin3xcos3xsin2xcos2x1，A错误；对B：当x1时
 1   1  1 1 3 3 1 1 1 1
f x2 f x1 2 x x1 2  x1 x2  x2  x1 2 x x1 2  x1 x2  x1 2 x2 0，故
   
f  x 1 2   f   x1 1 2  xx1 1 2 x1x 1 2，即 f  2022   f  2023  2022 20232023 2022，B正确；
   
对C：∵ f  x21   f 2x ，且 f xx3 在R上单调递增，∴x212x，解得x1，C正确；对D：构建
gx fxsinx，则gx 在R上连续不断，则有：当x1时，则 fxx3 1,sinx1，故
gx f xsinx110，可得gx 在 1, 内无零点；当x1时，则 fxx31,sinx1，故
gx f xsinx110，可得gx 在 ,1 内无零点；当1x1时，则
g11sin1 1sin10,g1 1sin10，故gx
在区间
1,1 内存在零点；综上所述：gx
只在区
间
1,1
内存在零点，即方程
fxsinx的解都在区间 1,1
内，D正确.故选：BCD.
高三数学答案 第 2 页 共 6 页
学科网（北京）股份有限公司 
13．36 14．90 15． 2, 16． 5
17．
2 1
(1)第3次传球之前，球在甲手中的情形何分为：甲→乙→甲或甲→丙→甲，所以p   ，第3次传球
3 4 2
1
之前，球在乙手里的情形仅有：甲→丙→乙，所以q  ，所以p 2q 1.
3 4 3 3
 1 1  1 1
p  q  (1 p q ) p   p
  n1 2 n 2 n n   n1 2 2 n
(2)由题意知 ，整理得：
 q  1 p  1 (1 p q )  q  1  1 q
 n1 2 n 2 n n  n1 2 2 n
1 1 1 1 2  1 2 1
所以 p   p  ，p   ，所以p  成首项为 ，公比为 的等比数列，
n1 3 2 n 3 1 3 3  n 3 3 2
1 2  1 n1 1 2  1 n1  1 1 1
又p n  3  3    2    p n  3  3    2   ，同理  q n  3   成首项为 3 ，公比为 2 的等比数列，
1 1  1 n1 1 1  1 n1 1 2  1 7 1 1  1 7 1 1
所以q     q     。因为p     ，q     ，p  ，q  ，
n 3 3  2 n 3 3  2 8 3 3  2 8 3 3  2 8 3 8 3
所以p q ．
8 8
18．
(1)证明：选①， coshx  2  sinhx  2 


ex ex 

2



ex ex 

2

e2x e2x 2

e2x e2x 2
1；
 2   2  4 4
e2xe2x
 exex exex
选②，sinh2x  2  2sinh x cosh x；
2 22
选③，cosh2x
e2x e2x



ex ex 

2



ex ex 

2
 coshx  2  sinhx  2 .
2  2   2 
e2xe2x exex exex
ycosh2xsinhx   ，令tsinhx ，
2 2 2
因为函数y
ex
、y
ex
均为R上的增函数，故函数ysinhx
也为R上的增函数，
2 2
故tsinhx
exex
R，则t2 
e2xe2x2
，所以cosh2x2t21，
2 4
高三数学答案 第 3 页 共 6 页
学科网（北京）股份有限公司所以y2t2 t12  t 1  2  7  7 ，当且仅当t  1 时取“”，所以ycosh2xsinhx 的最小值为 7 .
 4 8 8 4 8
  ecosx ecosx esinx esinx
(2)证明：x  , ，coshcosxsinhsinx  ecosxecosx esinxesinx ，
 4 2 2
当x,0 时，ecosx ecosx 0 ，sinx0sinx，所以esinx esinx，所以esinx esinx 0，所以
     
ecosx ecosx esinx esinx 成立；当x0, 时，则0 x x ，且正弦函数ysinx在0, 上为增
 4 2 2  2
 
函数，cosxsin xsinx，所以ecosx esinx，esinx 0ecosx，所以ecosx ecosx esinx esinx 成立，
 2 
 
综上，x  , ，coshcosxsinhsinx .
 4
19．
5 5
(1)设v x，则  yb va  ，y5.16，v1.68， v2 x 15，
i i
i1 i1
5
v y 5vy
i i 45.1051.685.16 1.756
所以b   i1   1.98，a   yb  v5.161.981.681.83.
 5 v25v 2 1551.682 0.888
i
i1
所以 y 关于x的回归方程为  y1.98 x1.83.
(2)因为中国在线直播购物用户选择在品牌官方直播间购物与不在品牌官方直播间购物的人数之比为4：1，
按照分层抽样从这两类用户中抽取5人，则选择在品牌官方直播间购物的用户为4人，记作1,2,3,4，
不在品牌官方直播间购物的用户为1人，记作5，
从这5人随机抽取2人，结果有：
1,2,1,3,1,4,1,5,2,3, 2,4, 2,5 , 3,4 , 3,5 , 4,5 
，共10种，
其中2人全是选择在品牌官方直播间购物用户的结果为：
1,2,1,3,1,4,2,3,2,4,3,4
，共6种，
6 3
所以这2人全是选择在品牌官方直播间购物用户的概率为  .
10 5
20．
（1）因为OF//面BCDE，面BCDE面ABCBC，OF 面ABC，所以OF//BC，因为M 是BC的中
1 1
点，ABC是等边三角形，所以AM  BC，因为在矩形BCDE中，M ，N 分别是BC，DE的中点，所以
1
MN//CD，又BCCD，所以MNBC，又MNAM M，MN,AM 面AMN，所以BC面AMN，
1 1 1 1
高三数学答案 第 4 页 共 6 页
学科网（北京）股份有限公司因为OF//BC，所以OF 面AMN.
1
（2）在线段ND上取点G使得DG2，连接GO,ON ，因为O是等边三角形ABC的中心，OF//BC，所
1
以OF:CM 2:3，因为CM  BC3，所以OF 2，所以DGOF，因为OF//BC，DG//BC，所以
2
DG//OF，所以四边形DFOG为平行四边形，所以DF//OG，所以DF和面AMN所成角等于OG和面
1
AMN所成角，由（1）得OF 面AMN，又DG//OF，所以DG面AMN，即GN 面AMN，所以OG
1 1 1 1
1
和面AMN的所成角为GON，即sinGON为所求，在RtGON 中，NGDNDG1,ON  AB3，
1 2 1
 sinGON 1
NG 1 π tanGON  
则tanGON   ，因为0GON  ，所以sinGON 0，联立 cosGON 3 ，解
ON 3 2  sin2GONcos2GON 1
10 10
得sinGON  ，所以DF和面AMN所成角的正弦值为 .
1
10 10
.
21．
3p
 p  8 11
（1）因为点F ,0到直线l :3x4y110的距离为 ，则有 2 8，而0 p10，
 2  1 5 
3242 5
解得 p2，又曲线C是平面内到直线l :x1与点F1,0 的距离相等的点的轨迹，所以轨迹C为抛物线，
2
方程为y2 4x．
3x4y110
（2）由 消去x并整理得：3y216y440，又点A在第一象限，于是得点A的纵坐标y 2，
y2 4x A
1
而直线l :x1交x轴于点B(1,0)，则 BF 2，所以△ABF 的面积S  |BF|y 2.
2 2 A
22．
高三数学答案 第 5 页 共 6 页
学科网（北京）股份有限公司2
 1 3 1 1 3
（1）y f xgx  x2x1  x   ，x 0,1  ，因为x 0,1  ，所以x   , ，则
 2 4 2 2 2
2
 1 3
y x   1,3 ，故函数 f x 与gx 的“偏差”为3；
 2 4
（2）令tx f xg xx2xb  x 1  2 b 1 ，x1,1  ，hx tx   x 1  2 b 1 ，
 2 4  2 4
x1,1  ，因为x1,1  ，x 1     3 , 1 ，  x 1  2    0, 9   ，当b 1 0，即b 1 时，此时
2  2 2  2  4 4 4
 x 1  2 b 1 0，则hx  x 1  2 b 1 的“偏差”为2b，由于2b 9 ；当b 1 0，即b 1 时，
 2 4  2 4 4 4 4
此时  x 1  2 b 1 0，则hx  x 1  2 b 1 的“偏差”为2b，由于2b 9 ；当b 1 0，
 2 4  2 4 4 4
2
1 1 7  1 1
t12b0，且b 2b，即 b 时，则hx x  b 的“偏差”为2b，由于
4 4 8  2 4
2
9 9 1 1 7  1 1
2b ；当b 0，t12b0，且b 2b，即b 时，则hx x  b 的“偏
8 4 4 4 8  2 4
1 1 9 1 1 7
差”为b ，由于b  ；当b 0，t12b0，且b 2b，即b 时，则
4 4 8 4 4 8
2
 1 1 1 1 9 1
hx x  b 的“偏差”为b ，由于b  ；当b 0，t12b0，即b2时，则
 2 4 4 4 8 4
2
 1 1 1 1 9 1
hx x  b 的“偏差”为b ，由于b  ；当b 0，t12b0，即b2时，则
 2 4 4 4 4 4
2
 1 1 1 1 9
hx x  b 的“偏差”为b ，由于b  ；
 2 4 4 4 4
7
综上，b 时，满足要求.
8
高三数学答案 第 6 页 共 6 页
学科网（北京）股份有限公司