数学答案_2024年2月_01每日更新_03号_2024届山西省吕梁市高三上学期1月期末考试_山西省吕梁市2024届高三上学期1月期末考试数学

吕梁市2023-2024学年第一学期期末调研测试 一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中， 只有一项是符合题目要求的. 1. A 解：∵A＝（1，2），B＝（﹣∞，2），∴A∪B＝B，故选A． 1−i （1−i）(1−i) −2i 2.B 解：z= = = =−i,|z|=|−i|=1,故选: B. 1+i (1+i)(1−i) 2 3.A 解：由题意，得 ；故离心率为 . 4.D 解：由已知得 解得 则⃗AB⋅⃗AE=2×1=2 故选：D 5.D解： 故选：D. 6. C 解：如图，作出圆台的轴截面，设截面上部延长部分三角形的高为 ，由相似三角形性质，得 设水到达最大容量时水面的圆面半径为 ，则 如水的最大容量为 7. 解：由题意，得 当 时， 答案第1页，共8页 学科网（北京）股份有限公司8. D解：法一：令 ，故A正确； ， ，故B正确； ，令 ，故C正确. 令 法二：构造函数 二、选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合 题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分． 9.BCD解：对于A选项，“ ，”的否定为“ ”，故A错误； 对 于 B 选 项 ， 由 ， 因 此 ，故B正确； 答案第2页，共8页 学科网（北京）股份有限公司对于C选项， 故C正确. 对于D选项， ，故D正确.故选：BCD. 10.AD解：根据函数f（x）＝Asin（ x+ ）（A＞0， ＞0，| |＜ ）的部分图象， ω φ ω φ 可得A＝2， × ＝ + ，∴ ＝2， ω 对于A选项，结合五点法作图，可得2× + ＝ ，∴ ＝﹣ ，故A正确， φ φ f（x）＝2sin（2x﹣ ），将函数f（x）的图象平移后得到函数g（x）的图象， 则g（x）＝﹣2sin（2x+ ）， 对于B选项， 显然 不是其对称轴，故 ，故B错误， 对于C选项，函数g（x）显然不是奇函数，故C错误， 对于D 选项，∵﹣2＜0，∴g（x）递增区间即y＝sin（2x+ ）的递减区间， 令2k + ≤2x+ ≤2k + ，k Z， π π ∈ 解得k + ≤x≤k + ，k Z， π π ∈ 故g（x）的递增区间是[k + ，k + ]（k Z）， π π11π 5∈π 当k＝-1时，g（x）的递增区间是[− ，− ]， 12 12 故D正确，故选：AD． 答案第3页，共8页 学科网（北京）股份有限公司11.ABD解：对于A选项，当 时，点 在平面 内，易得 , ,故A正确； 对于B选项，当 , ,故点 在直线 上，直线 即为直线 易得 ,故B正确； 对于C 选项， 当 当 时， ,故P为 的中点 易得， 连接 交 于点O，则 故C错误； 对于D 选项，当 ， 时， 则 ， 可知点 在平面 内， 因为平面 ∥平面 ， 则直线 与平面 所成角即为直线 与平面 所成的角， 因为 平面 ，则直线 与平面 所成的角为 ， 答案第4页，共8页 学科网（北京）股份有限公司可得 ， 又因为 ，即 ，则 可得 当且仅当 ，即 时，等号成立， 可知 的最小值为 ，则 的最大值 ， 所以直线 与平面 所成角的正切值的最大值为 ，故D正确.故选ABD. 12.AC解：当两切线分别与两坐标轴垂直时，两切线的方程分别为 、 ， 所以，点 在蒙日圆上，故蒙日圆的方程为 ， 因为 ，可得 . 对于A选项，蒙日圆圆心到直线 的距离为 ， 所以，直线 与蒙日圆相切，故A正确； x2  y2 4 对于B选项， 的蒙日圆的方程为 ，故B错误； l l 对于C选项，由题意可知， 1 2，所以MN为蒙日圆的直径，MN=4,故C正确； AF  AF 2 3 对于D选项，由椭圆的定义可得， 1 2 d  AF d  AF 2 3 所以， 2 1 ， x 3y40 直线 的方程为 ， 答案第5页，共8页 学科网（北京）股份有限公司4 2 d  点 到直线 的距离为 1 2 ， 4 24 3 d  AF d  AF 2 3 d 2 3  所以， 2 1 1 2 ， 当且仅当 时，等号成立，故D错误； 故选：AC. 三､填空题：本题共4小题，每小题5分，共20分. 13. 20 解： 的第 项为 ， 令 代入通项可得 展开式中的 和 项分别为： ，分别与 和 相乘， 得 的展开式中 项为 ，故 的系数为20.故为：20 14. 解：依题意， ， ， 代入回归直线 ，解得 所以回归直线为 当 时， ，因此残差为 ， 15. 解： 答案第6页，共8页 学科网（北京）股份有限公司. 16. 解：点 可知： 又 由 知， 和 在 上单调递增 ，其值域为Rx 令 令 答案第7页，共8页 学科网（北京）股份有限公司所以，实数 的最大值为 . 四、解答题:本题共6小题,共70分．解答应写出文字说明、证明过程或演算步骤． 17．（1） ;(2) . 解：（1）由题意，得 当 ...................................................3分 当 ,适合上式. ...................................................4分 ...................................................5分 (2) ...................................................7分 ......................10分 18.（1） ;(2)9 解：（1） . ......................1分 ..................................3分 .................................4分 .................................5分 （2） 答案第8页，共8页 学科网（北京）股份有限公司........................................................8分 ..........................................11分 当且仅当 ，等号成立， 所以 的最小值为9. 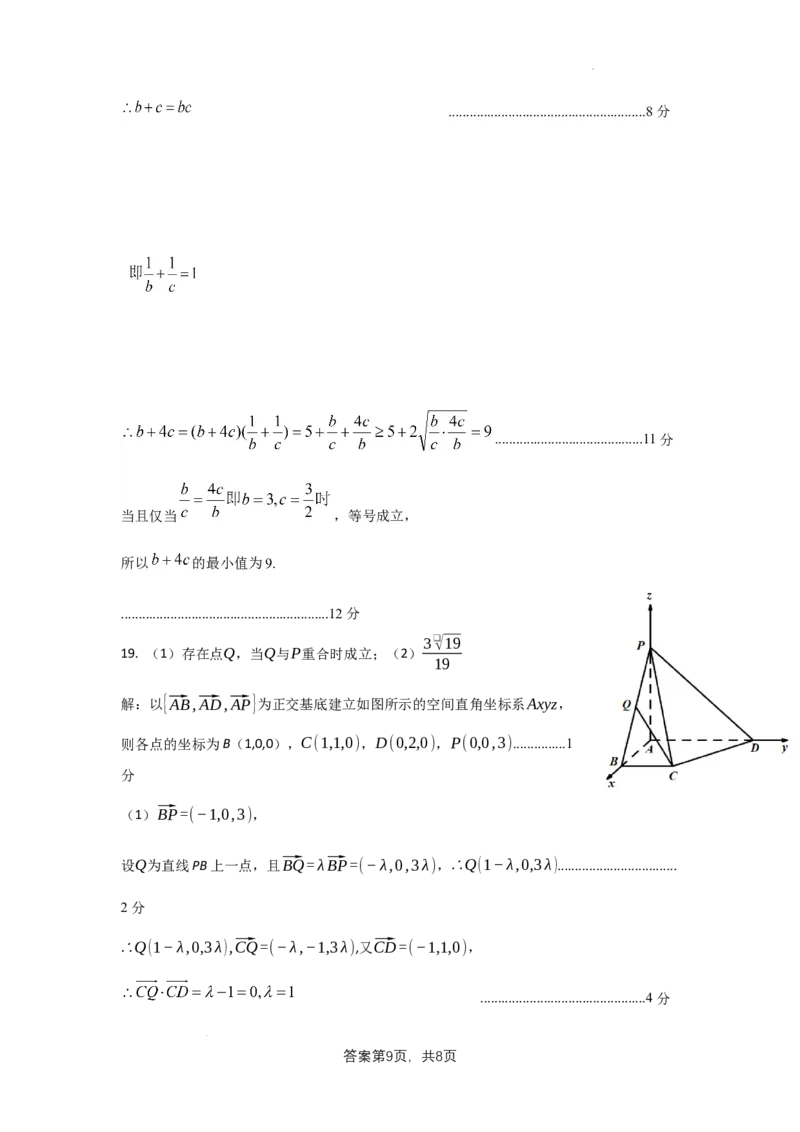...........................................................12分 3❑√19 19. （1）存在点Q，当Q与P重合时成立；（2） 19 解：以{⃗AB,⃗AD,⃗AP}为正交基底建立如图所示的空间直角坐标系Axyz， 则各点的坐标为B（1,0,0），C(1,1,0)，D(0,2,0)，P(0,0,3)...............1 分 （1）⃗BP=(−1,0,3)， 设Q为直线PB上一点，且⃗BQ=λ⃗BP=(−λ,0,3λ)，∴Q(1−λ,0,3λ).................................. 2分 ∴Q(1−λ,0,3λ),⃗CQ=(−λ,−1,3λ),又⃗CD=(−1,1,0)， ...............................................4分 答案第9页，共8页 学科网（北京）股份有限公司QC CD 所以存在点Q，满足 ，此时BQ=1. .................................................................5分 （2）由（1）可得 ， 又Q(1−λ,0,3λ),⃗CQ=(−λ,−1,3λ) 则点 到直线 的距离d=❑√⃗CQ2−(|⃗CQ|cos⟨⃗CQ,⃗CD⟩) 2 =❑ √ ⃗CQ2− ( ⃗CQ•⃗CD) 2 |⃗CD| .............7分 =❑ √ λ2+1+9λ2− ( λ−1 ) 2 =❑ √19 λ2+λ+ 1 ........................................................................9分 ❑√1+1 2 2 ∵ 19 λ2+λ+ 1 = 19( λ+ 1 ) 2 + 9 ≥ 9 2 2 2 19 19 19 3❑√19 ∴d≥ ............................................11 19 分 3❑√19 所以异面直线PB与CD之间的距离为 .......................................................................12分 19 1 20. (1)2 (2)小李能进入决赛 解：(1)设A＝“在一轮比赛中，小李获得通关卡”，则事件A发生的所有情况有： C1C1C2 3 1 P  3 1 2   ①得到认可的中式面点入选1道，中式热菜入选2道的概率为 1 C2C2 66 12 4 4 C2C1C1 12 1 P  3 2 2   ②得到认可的中式面点入选2道，中式热菜入选1道的概率为 2 C2C2 66 3 4 4 C2C2 3 1 P  3 2   ③得到认可的中式面点和中式热菜各入选2道的概率为 3 C2C2 66 12 4 4 1 1 1 1 所以PA    ； .........................................................................5分 12 3 12 2 3 (2)由题知，强化训练后，每道中式面点被评委认可的概率为 ，每道中式热菜被评委认可 4 答案第10页，共8页 学科网（北京）股份有限公司1 1 2 的概率为 + = ，则强化训练后，在一轮比赛中，小李获得通关卡的概率为 2 6 3 3 1 2 2 3 2 2 1 3 2 2 2 1 1 1 2 PC1  C2  C2  C1  C2  C2      2 4 4 2 3 2 4 2 3 3 2 4 2 3 6 4 4 3 ，.....8分 因为每轮比赛结果互不影响，所以进行3轮比赛可看作3重伯努利试验．  2 X B3,  用X表示小李在3轮比赛中获得通关卡的次数，则  3 ....................10分 2 ∴EX3 2， 3 ∴小李能进入决赛 ...................................................................................12分 21．（1）抛物线 C 的方程为 ，点 A 的坐标为 ；（2）直线 的方程为 . 解：（1）联立 ，消 得 ， 因为直线 与抛物线 相切， 所以 ，解得 或 （舍去）， ...................................................2 分 当 时， ，解得 ，所以 ， ...............................................4分 所以抛物线C的方程为 ，点A的坐标为 ； ..............................................5分 （2）显然直线 的斜率存在， 可设为 ， 由 ，消 得 ， 则 ， 答案第11页，共8页 学科网（北京）股份有限公司， .............................................7分 ， 因为以MN为直径的圆过点A， 所以 ， 即 ， .....................................................8分 整理可得 ， 所以 ， 化简得 ， 所以 ， 所以 或 ， 即 或 ， ...........................................................9分 当 时，直线 ， 即 ，所以直线 过定点 （舍去）， 当 时，直线 ，满足 ， 即 ，所以直线 过定点 ， ................................................10分 设点A到直线PQ的距离为d，则 ...............................................................11分 当直线 与 垂直时，d最大 又 ，所以 ， 答案第12页，共8页 学科网（北京）股份有限公司所以直线 的方程为 . ...............................................................12分 22.（1） (2) 解：（1） ， ...............................................................1 分 ...............................................................2分 ...............................................................3分 故切线方程为 ............................4分 （2）由题意，得 对任意x R， ≥0恒成立， ∈ 令g（x）＝ ，则g′（x）＝ax﹣a+ex+sinx， 令h（x）＝ax﹣a+ex+sinx，则h′（x）＝a+ex+cosx， ............................5分 当a＞1时，h′（x）＞0，g′（x）单调递增，且g′（0）＝1﹣a＜0，g′（1）＝ e+sin1＞0， 所以存在x （0，1）使得g′（x ）＝0， 0 0 当x （0，x∈0 ）时，g′（x）＜0，g（x）单调递减，当x （x 0 ，+∞）时，g′（x）＞ 0，g∈（x）单调递增， ∈ 所以g（x）＜g（0）＝0，不合题意； .. ....................................................7分 当a＝1时，h′（x）＞0，g′（x）单调递增，且g′（0）＝0， 当x （0，+∞）时，g′（x）＞0，g（x）单调递增，当x （﹣∞，0）时，g′（x） ＜0，∈g（x）单调递减， ∈ 所以g（x）≥g（0）＝0，符合题意； . . ....................................................9分 当0＜a＜1时，h′（x）在（﹣1，0）上单调递增， 又h′（﹣1）＝a+ +cos1＞0， 所以h′（x）＞h′（﹣1）＞0，g′（x）在（﹣1，0）上单调递增， 答案第13页，共8页 学科网（北京）股份有限公司又g′（0）＝1﹣a＞0， ＝ ＜ 0， 所以存在m （﹣1，0）使得g′（m）＝0， 当x （m，∈0）时，g′（x）＞0，g（x）单调递增，g（x）＜g（0）＝0，不符合题意， ∈ ....................................................11分 综上，正实数a的取值集合为{1}． ....................................................12分 答案第14页，共8页 学科网（北京）股份有限公司