文档内容
专题 1.1 空间向量及其线性运算【八大题型】
【人教A版(2019)】
【题型1 空间向量概念的理解】..............................................................................................................................2
【题型2 空间向量的加减运算】..............................................................................................................................3
【题型3 空间向量的线性运算】..............................................................................................................................3
【题型4 由空间向量的线性运算求参数】..............................................................................................................4
【题型5 向量共线的判定及应用】..........................................................................................................................6
【题型6 由空间向量共线求参数】..........................................................................................................................8
【题型7 向量共面的判定及应用】..........................................................................................................................9
【题型8 由空间向量共面求参数】........................................................................................................................10
【知识点1 空间向量的概念】
1.空间向量的概念
(1)定义:在空间,具有大小和方向的量叫做空间向量.
(2)长度或模:向量的大小.
(3)表示方法:
①几何表示法:空间向量用有向线段表示;
②字母表示法:用字母a,b,c,…表示;若向量a的起点是A,终点是B,也可记作AB,其模记为|
a|或|AB|.
(4)几类特殊的空间向量
名称 定义及表示
零向量 长度为0的向量叫做零向量,记为0
单位向量 模为1的向量称为单位向量
与向量a长度相等而方向相反的向量,称为a的相反向量,记为 -
相反向量
a
如果表示若干空间向量的有向线段所在的直线互相平行或重合,那
共线向量
么这些向量叫做共线向量或平行向量.规定:对于任意向量a,都
(平行向量)
有0∥a
相等向量 方向相同且模相等的向量称为相等向量
【注】(1)空间中点的一个平移就是一个向量;
学科网(北京)股份有限公司(2)数学中讨论的向量与向量的起点无关,只与大小和方向有关,只要不改变大小和方向,空间向量
可在空间内任意平移,故我们称之为自由向量.
【题型1 空间向量概念的理解】
【例1】(2023春·高二课时练习)下列命题中是假命题的是( )
A.任意向量与它的相反向量不相等
B.和平面向量类似,任意两个空间向量都不能比较大小
C.如果|⃗a|=0,则⃗a=0⃗
D.两个相等的向量,若起点相同,则终点也相同
【变式1-1】(2023·江苏·高二专题练习)下列说法正确的是( )
A.任一空间向量与它的相反向量都不相等
B.不相等的两个空间向量的模必不相等
C.同平面向量一样,任意两个空间向量都不能比较大小
D.将空间向量所有的单位向量平移到同一起点,则它们的终点构成一个圆
【变式1-2】(2023秋·高二课时练习)给出下列命题:
①若将空间中所有的单位向量的起点移到同一个点,则它们的终点构成一个圆;②若空间向量⃗a,⃗b满足
|⃗a|=|⃗b|,则⃗a=⃗b;③若空间向量⃗m,⃗n,⃗p满足⃗m=⃗n,⃗n=⃗p,则⃗m=⃗p;④空间中任意两个单位向量必
相等;⑤零向量没有方向.
其中假命题的个数是( ).
A.1 B.2 C.3 D.4
【变式1-3】(2023秋·高二课时练习)给出下列命题:
①零向量没有方向;
②若两个空间向量相等,则它们的起点相同,终点也相同;
③若空间向量 满足 ,则 ;
⃗a,⃗b |⃗a|=|⃗b| ⃗a=⃗b
④若空间向量⃗m,⃗n,⃗p满足⃗m=⃗n,⃗n=⃗p,则⃗m=⃗p;
⑤空间中任意两个单位向量必相等.
其中正确命题的个数为( )
A.4 B.3
C.2 D.1
【知识点2 空间向量的线性运算】
1.空间向量的线性运算
空间向 加法 a+b=OA+ AB =OB
学科网(北京)股份有限公司减法 a-b=OA-OC=CA
量的线
性运算 当λ>0时,λa=λOA=PQ;
数乘 当λ<0时,λa=λOA=MN;
当λ=0时,λa=0
交换律:a+b=b+a;
运算律 结合律:a+(b+c)=(a+b)+c,λ(μa)=(λμ)a;
分配律:(λ+μ)a=λa+μa,λ(a+b)=λa+λb.
【注】(1)空间向量的运算是平面向量运算的延展,空间向量的加法运算仍然满足平行四边形法则和三
角形法则,而且满足交换律、结合律,这样就可以自由结合运算,可以将向量合并.
(2)向量的减法运算是向量加法运算的逆运算,满足三角形法则.
(3)空间向量加法的运算的小技巧:
①首尾相接的若干向量之和,等于由起始向量的起点指向末尾向量的终点的向量,因此,求空间若干
向量之和时,可通过平移使它们转化为首尾相接的向量;
②首尾相接的若干向量若构成一个封闭图形,则它们的和为零向量.
【题型2 空间向量的加减运算】
【例2】(2023春·高二课时练习)在四面体OABC中,⃗OA+⃗AB−⃗CB等于( )
A.⃗OA B.⃗AB C.⃗OC D.⃗AC
【变式2-1】(2023春·江苏连云港·高二校联考期中)正方体ABCD−A B C D 中,化简
1 1 1 1
( )
⃗AB+⃗BD−⃗AC =
1
A. B. C. D.
⃗C B ⃗BC ⃗C D ⃗DC
1 1 1 1
【变式2-2】(2023春·高二课时练习)在空间四边形ABCD 中,连接AC ,BD ,若△BCD 是正三角
1 3
形,且E 为其重心,则⃗AB+ ⃗BC− ⃗DE−⃗AD=( )
2 2
A.⃗AB B.2⃗BD C.0⃗ D.2⃗DE
【变式2-3】(2023·全国·高三专题练习)空间四边形ABCD中,若E、F、G、H分别为AB、BC、CD、
DA边上的中点,则下列各式中成立的是
A. + + + → B. + + →
⃑EB ⃑BF ⃑EH
⃑GH=0
⃑EB ⃑FC
⃑EH –⃑EG=0
C. + + + → D. + + →
⃑EF ⃑FG ⃑EH
⃑GH=0
⃑EF–⃑FB ⃑CG
⃑GH=0
学科网(北京)股份有限公司【题型3 空间向量的线性运算】
【例3】(2023春·高二单元测试)若A,B,C,D为空间不同的四点,则下列各式不一定为零向量的是
( )
A.⃗AB+2⃗BC+2⃗CD+⃗DC
B.2⃗AB+2⃗BC+3⃗CD+3⃗DA+⃗AC
C.⃗AB+⃗DA+⃗BD
D.⃗AB−⃗CB+⃗CD−⃗AD
【变式3-1】(2023秋·新疆昌吉·高二校考期末)已知正方体ABCD−A′B′C′D′,点E是A′C′的中点,点
1
F是AE的三等分点,且AF= EF,则⃗AF等于( ).
2
1 1 1 1 1
A. ⃗ A A′+ ⃗AB+ ⃗AD B. ⃗ A A′+ ⃗AB+ ⃗AD
2 2 2 2 2
1 1 1 1 1 1
C. ⃗ A A′+ ⃗AB+ ⃗AD D. ⃗ A A′+ ⃗AB+ ⃗AD
2 6 6 3 6 6
【变式3-2】(2023秋·山东威海·高二统考期末)在平行六面体ABCD−A B C D 中,点E满足
1 1 1 1
1 1
⃗AE=− ⃗A A +⃗AB + ⃗AD ,则( )
3 1 1 3 1
A. B. C. D.
3⃗B E=⃗B C 3⃗B E=2⃗B C ⃗B E=3⃗B C 2⃗B E=3⃗B C
1 1 1 1 1 1 1 1 1 1 1 1
【变式3-3】(2023秋·安徽黄山·高二统考期末)如图,在三棱柱ABC−A B C 中,E、F分别是BC、
1 1 1
CC 的中点,G为△ABC的重心,则⃗GF=( )
1
1 2 1 1 2 1
A.− ⃗AB+ ⃗AC+ ⃗A A B. ⃗AB+ ⃗AC+ ⃗A A
3 3 2 1 3 3 2 1
学科网(北京)股份有限公司2 1 1 1 2 1
C.− ⃗AB+ ⃗AC− ⃗A A D. ⃗AB− ⃗AC+ ⃗A A
3 3 2 1 3 3 2 1
【题型4 由空间向量的线性运算求参数】
【例4】(2023春·湖南长沙·高二校考开学考试)如图所示,空间四边形OABC中,
,点 在 上,且 为 的中点, → → → →,则
⃗OA=⃗a,⃗OB=⃗b,⃗OC=⃗c M ⃗OA ⃗OM=2⃗MA,N BC
MN=xa+ yb+zc
x,y,z
的值分别为( )
1 2 1 1 1 2
A. ,− , B. , ,−
2 3 2 2 2 3
2 1 1 2 2 1
C.− , , D. , ,−
3 2 2 3 3 2
【变式4-1】(2023秋·湖南娄底·高二校联考期末)在三棱柱ABC−A B C 中,D是CC 的中点,F是
1 1 1 1
A B的中点,且⃑DF=α⃑AB+β⃑AC,则
1
1 1
A.α= , β=−1 B.α=− , β=1
2 2
1 1
C.α=1, β=− D.α=−1, β=
2 2
【变式4-2】(2023秋·山东泰安·高二校考期末)如图所示,在平行六面体ABCD−A B C D 中,点E
1 1 1 1
为上底面对角线A C 的中点,若⃑BE=⃑A A +x⃑AB+ y⃑AD,则( )
1 1 1
学科网(北京)股份有限公司1 1 1 1
A.x=− ,y= B.x= ,y=−
2 2 2 2
1 1 1 1
C.x=− ,y=− D.x= ,y=
2 2 2 2
【变式4-3】(2023春·高二课时练习)在平行六面体ABCD−A B C D 中,点P在A C上,且
1 1 1 1 1
1
⃗A P= ⃗A C,若⃗AP=x⃗A A + y⃗AB+z⃗AD,则x+ y+z=( )
1 4 1 1
3 5 7
A. B.1 C. D.
4 4 4
【知识点3 共线向量与共面向量】
1.共线向量
(1)空间两个向量共线的充要条件
对于空间任意两个向量a,b(b≠0),a∥b的充要条件是存在实数λ,使a=λb.
(2)直线的方向向量
在直线l上取非零向量a,我们把与向量a平行的非零向量称为直线 l 的方向向量.
规定:零向量与任意向量平行,即对任意向量a,都有0//a.
(3)共线向量定理的用途:
①判定两条直线平行;
②证明三点共线.
【注】:证明平行时,先从两直线上取有向线段表示两个向量,然后利用向量的线性运算证明向量共
线,进而可以得到线线平行,这是证明平行问题的一种重要方法;证明三点共线问题,通常不用图形,直
接利用向量的线性运算即可,但一定要注意所表示的向量必须有一个公共点.
2.共面向量
(1)共面向量
如图,如果表示向量a的有向线段OA所在的直线OA与直线l平行或重合,那么称向量a平行于直线l.
如果直线OA平行于平面α或在平面α内,那么称向量a平行于平面α.平行于同一个平面的向量,叫做共
面向量.
学科网(北京)股份有限公司(2)向量共面的充要条件
如果两个向量a,b不共线,那么向量p与向量a,b共面的充要条件是存在唯一的有序实数对(x,y),
使p=xa+yb.
(3)共面向量定理的用途:
①证明四点共面;
②证明线面平行.
【题型5 向量共线的判定及应用】
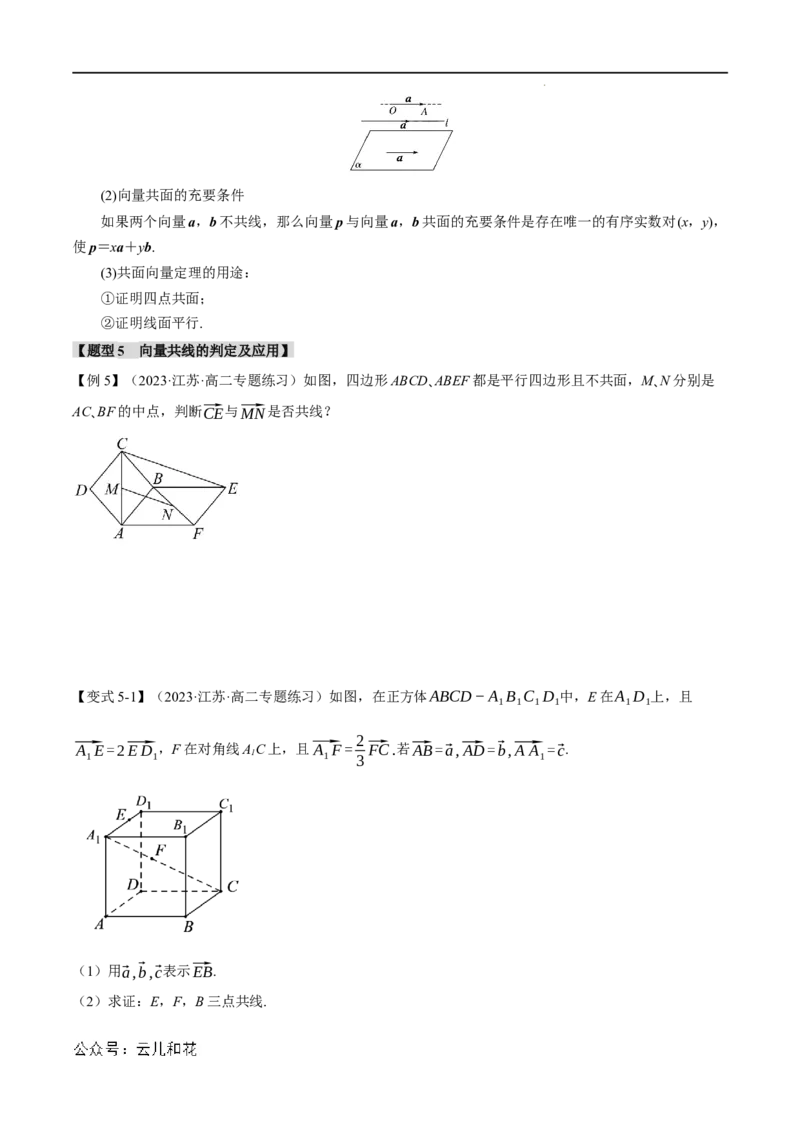
【例5】(2023·江苏·高二专题练习)如图,四边形ABCD、ABEF都是平行四边形且不共面,M、N分别是
AC、BF的中点,判断⃗CE与⃗MN是否共线?
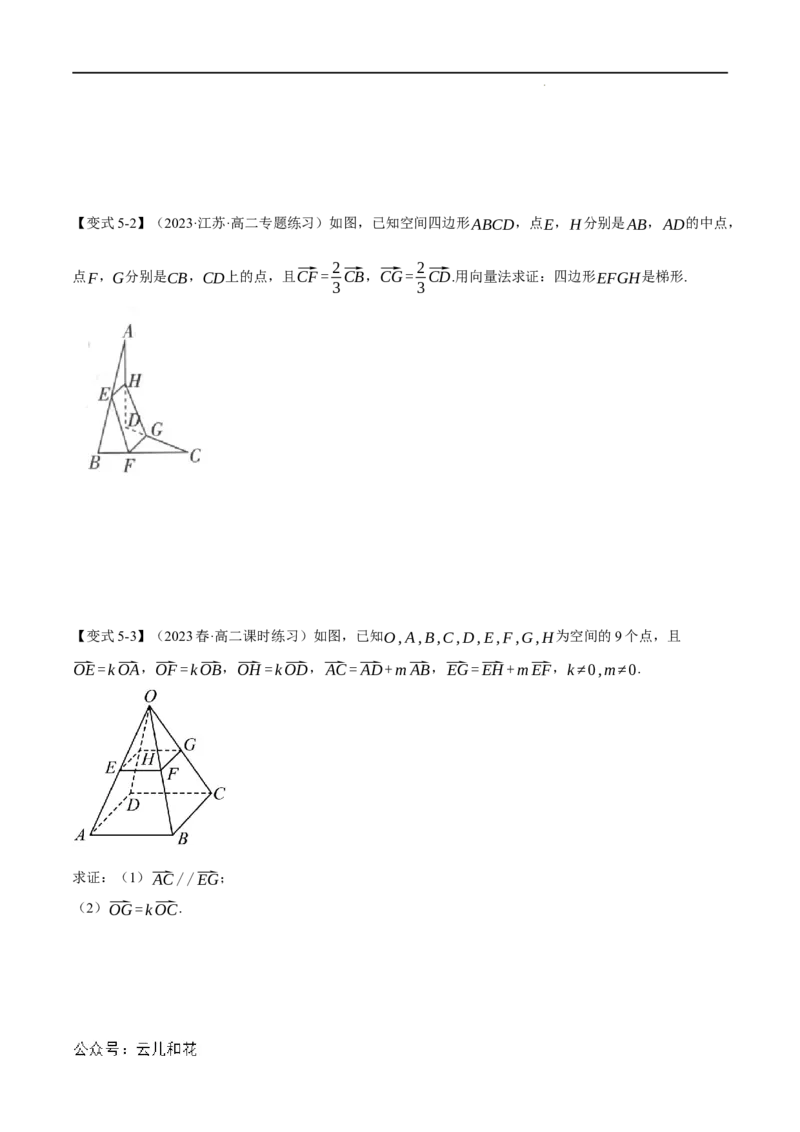
【变式5-1】(2023·江苏·高二专题练习)如图,在正方体ABCD−A B C D 中,E在A D 上,且
1 1 1 1 1 1
2
⃗A
1
E=2⃗ED
1
,F在对角线A
1
C上,且⃗A
1
F=
3
⃗FC.若⃗AB=⃗a,⃗AD=⃗b,⃗A A
1
=⃗c.
(1)用⃗a,⃗b,⃗c表示⃗EB.
(2)求证:E,F,B三点共线.
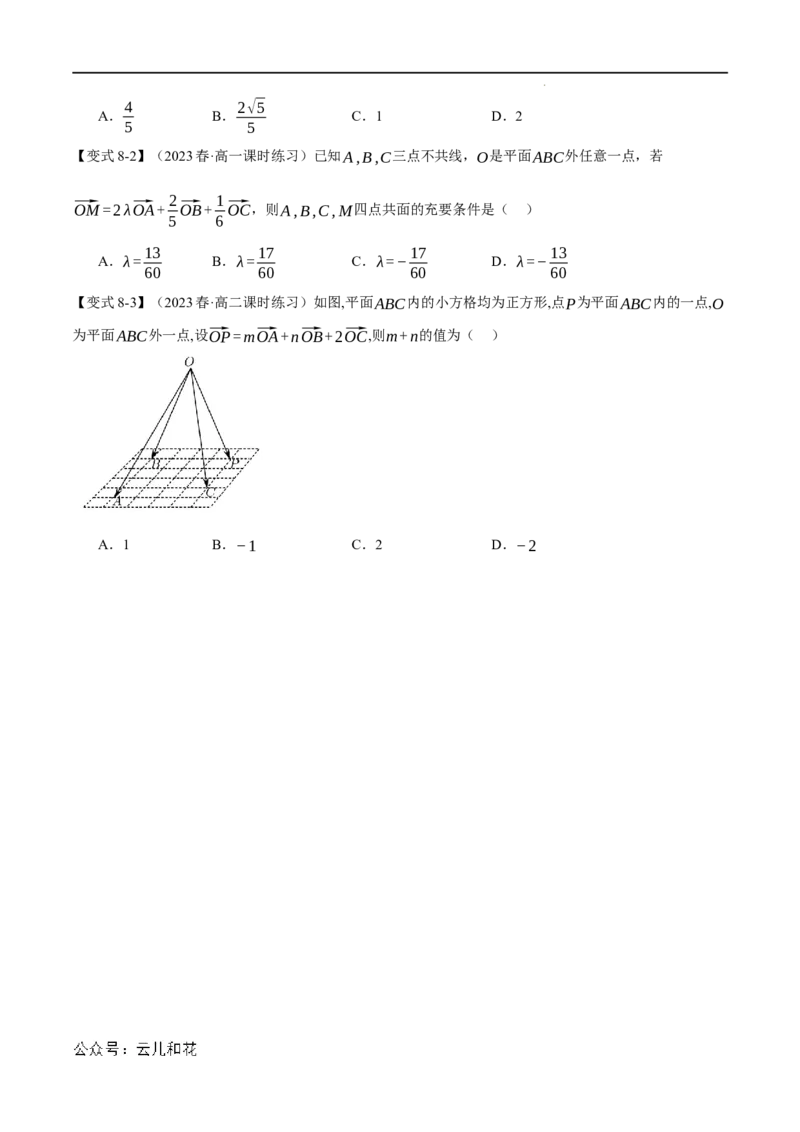
学科网(北京)股份有限公司【变式5-2】(2023·江苏·高二专题练习)如图,已知空间四边形ABCD,点E,H分别是AB,AD的中点,
2 2
点F,G分别是CB,CD上的点,且⃗CF= ⃗CB,⃗CG= ⃗CD.用向量法求证:四边形EFGH是梯形.
3 3
【变式5-3】(2023春·高二课时练习)如图,已知O,A,B,C,D,E,F,G,H为空间的9个点,且
⃑OE=k⃑OA,⃑OF=k⃑OB,⃑OH=k⃑OD,⃑AC=⃑AD+m⃑AB,⃑EG=⃑EH+m⃑EF,k≠0,m≠0.
求证:(1)⃑AC//⃑EG;
(2)⃑OG=k⃑OC.
学科网(北京)股份有限公司【题型6 由空间向量共线求参数】
【例6】(2023春·福建龙岩·高二校联考期中)设向量 , , 不共面,已知 ,
⃗e ⃗e ⃗e ⃗AB=⃗e +⃗e +⃗e
1 2 3 1 2 3
, ,若A,C,D三点共线,则 ( )
⃗BC=⃗e +λ⃗e +⃗e ⃗CD=4⃗e +8⃗e +4⃗e λ=
1 2 3 1 2 3
A.1 B.2 C.3 D.4
【变式6-1】(2022秋·新疆阿勒泰·高二校联考期末)如果空间向量⃗a,⃗b不共线,且⃗a−y⃗b=x⃗a+3⃗b,那
么x,y的值分别是( )
A.x=−1,y=3 B.x=−1,y=−3
C.x=1,y=−3 D.x=1,y=3
【变式6-2】(2023春·江苏南京·高二校考阶段练习)已知{⃑a,⃑b,⃑c}是空间的一个基底,若⃑m=⃑a+2⃑b−3⃑c,
x
⃑n=x(⃑a+⃑b)−y(⃑b+⃑c)+3(⃑a+⃑c),若⃑m∥⃑n,则 =( )
y
1 1
A.−3 B.− C.3 D.
3 3
【变式6-3】(2023春·高二课时练习)已知非零向量⃑a=3⃑m−2⃑n−4⃑p,⃑b=(x+1)⃑m+8⃑n+2y⃑p,且⃑m、
⃑n、⃑p不共面.若⃑a//⃑b,则x+ y=( )
A.−13
B.−5
C.8
D.13
【题型7 向量共面的判定及应用】
【例7】(2023春·高一课时练习)已知A,B,M三点不共线,对于平面ABM外的任意一点O,判断在下
列各条件下的点P与点A,B,M是否共面.
(1)⃗OB+⃗OM=3⃗OP−⃗OA;
(2)⃗OP=4⃗OA−⃗OB−⃗OM.
学科网(北京)股份有限公司【变式7-1】(2023秋·高二课时练习)已知i⃗,⃗j,⃗k是不共面向量,
⃗a=i⃗−2⃗j+⃗k,⃗b=−i⃗+3⃗j+2⃗k,⃗c=−3i⃗+7⃗j,证明这三个向量共面.
【变式7-2】(2023春·高二课时练习)已知E,F,G,H分别是空间四边形ABCD的边AB,BC,CD,
DA的中点,求证:
(1)E,F,G,H四点共面;
(2)BD∥平面EFGH.
【变式7-3】(2023秋·高二课时练习)已知平行四边形ABCD,从平面AC外一点O引向量⃑OE=k⃑OA,
⃑OF=k⃑OB,⃑OG=k⃑OC,⃑OH=k⃑OD.
(1)求证:E,F,G,H四点共面;
(2)平面AC∥平面EG.
【题型8 由空间向量共面求参数】
【例8】(2023春·四川绵阳·高二校考阶段练习)已知O为空间任意一点,A,B,C,P四点共面,但任意三
点不共线.如果⃗BP=m⃗OA+⃗OB+⃗OC,则m的值为( )
A.-2 B.-1 C.1 D.2
【变式8-1】(2023·全国·高二专题练习)已知点D在△ABC确定的平面内,O是平面ABC外任意一点,
实数x,y满足⃗OD=x⃗OA+ y⃗OB−⃗OC,则x2+ y2的最小值为( )
学科网(北京)股份有限公司4 2√5
A. B. C.1 D.2
5 5
【变式8-2】(2023春·高一课时练习)已知A,B,C三点不共线,O是平面ABC外任意一点,若
2 1
⃗OM=2λ⃗OA+ ⃗OB+ ⃗OC,则A,B,C,M四点共面的充要条件是( )
5 6
13 17 17 13
A.λ= B.λ= C.λ=− D.λ=−
60 60 60 60
【变式8-3】(2023春·高二课时练习)如图,平面ABC内的小方格均为正方形,点P为平面ABC内的一点,O
为平面ABC外一点,设⃗OP=m⃗OA+n⃗OB+2⃗OC,则m+n的值为( )
A.1 B.−1 C.2 D.−2
学科网(北京)股份有限公司