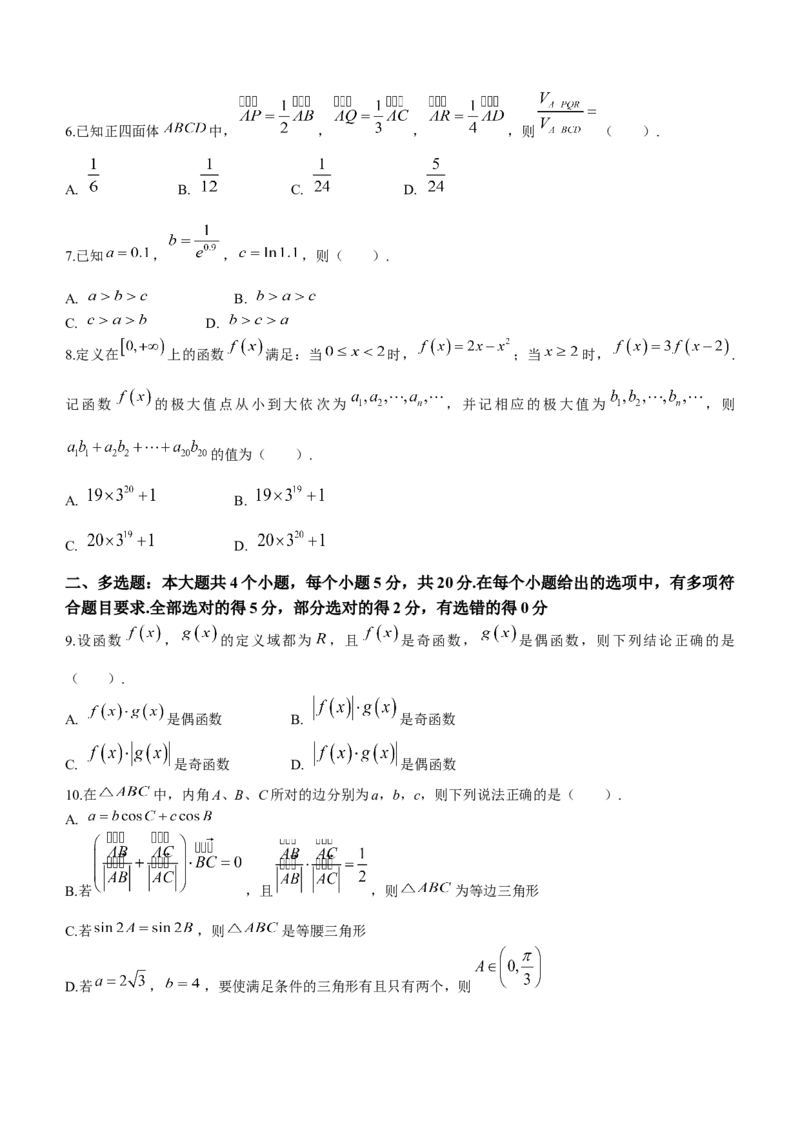文档内容
曲靖一中 2024 届高三教学质量监测试卷(四)
数学
命题人:张连吉 审题人:赵宇
考试时间:120分钟;满分:150分.
本试卷分为第I卷(选择题)和第Ⅱ卷(非选择题)两部分.
第Ⅰ卷(选择题,共60分)
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符
合题目要求的.
1.设集合 , ,则 ( )
A. B. C. D.
2.已知 ,则 ( )
A. B. C. D.2
3.已知向量 、 满足 , ,且 与 夹角的余弦值为 ,则 ( )
A.-36 B.-28 C. D.12
4.某市物价部门对本市5家商场的某种商品一天的销售量及其价格进行调查,5家商场这种商品的售价 (单
位;元)与销售量 (单位:件)之间的一组数据如下表所示:
价格 8 9. 10.5 12
5
销 售 量 16 8 6 5
经分析知,销售量 y件与价格 x元之间有较强的线性关系,其线性回归直线方程为 ,且
,则 ( ).
A.12 B.11 C.10 D.9
8.已知 ,则 ( ).
A. B. C. D.
学科网(北京)股份有限公司6.已知正四面体 中, , , ,则 ( ).
A. B. C. D.
7.已知 , , ,则( ).
A. B.
C. D.
8.定义在 上的函数 满足:当 时, ;当 时, .
记函数 的极大值点从小到大依次为 ,并记相应的极大值为 ,则
的值为( ).
A. B.
C. D.
二、多选题:本大题共4个小题,每个小题5分,共20分.在每个小题给出的选项中,有多项符
合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分
9.设函数 , 的定义域都为 ,且 是奇函数, 是偶函数,则下列结论正确的是
( ).
A. 是偶函数 B. 是奇函数
C. 是奇函数 D. 是偶函数
10.在 中,内角A、B、C所对的边分别为a,b,c,则下列说法正确的是( ).
A.
B.若 ,且 ,则 为等边三角形
C.若 ,则 是等腰三角形
D.若 , ,要使满足条件的三角形有且只有两个,则
学科网(北京)股份有限公司11.古希腊著名数学家阿波罗尼斯发现:平面内到两个定点 、 的距离之比为定值 的点所形
成的图形是圆.后来,人们将这个圆以他的名字命名,称为阿波罗尼斯圆,简称阿氏圆.已知在平面直角坐标系
中, , ,点 满足 ,设点 P 所构成的曲线为 C,下列结论正确的是
( ).
A.曲线C的方程为
B.在C上存在点D,使得D到点 的距离为10
C.在C上存在点M,使得
D.C上的点到直线 的最大距离为9
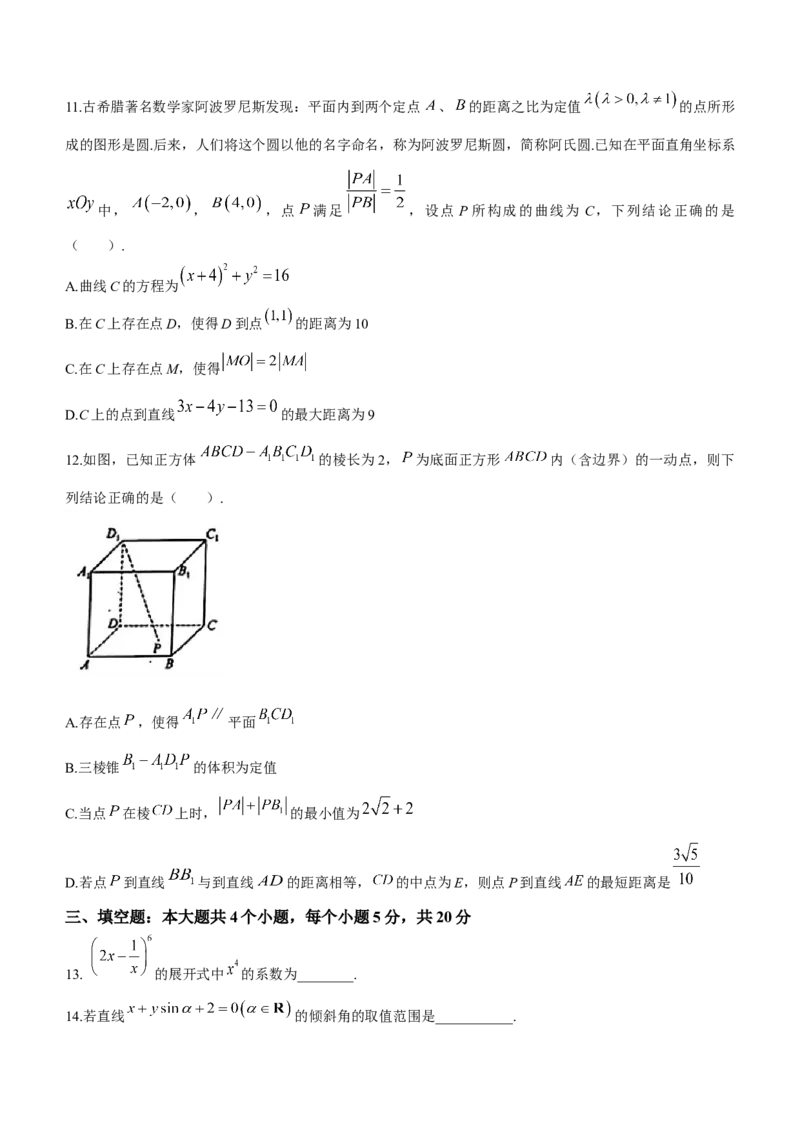
12.如图,已知正方体 的棱长为2, 为底面正方形 内(含边界)的一动点,则下
列结论正确的是( ).
A.存在点 ,使得 平面
B.三棱锥 的体积为定值
C.当点 在棱 上时, 的最小值为
D.若点 到直线 与到直线 的距离相等, 的中点为E,则点P到直线 的最短距离是
三、填空题:本大题共4个小题,每个小题5分,共20分
13. 的展开式中 的系数为________.
14.若直线 的倾斜角的取值范围是___________.
学科网(北京)股份有限公司15.若函数 与 的图像恰有一个公共点,则实数 的取值范围是________.
16.已知点 , 分别是双曲线 : 的左、右焦点,过点 的直线与双曲线的左、
右两支分别交于点P,Q.若 是以 为顶角的等腰三角形,其中 ,则双曲线
离心率 的取值范围为_________.
四、解答题:本大题共6个小题,共70分.解答应写出文字说明、证明过程或演算步骤
17.(本小题满分10分)观察下面的图形及相应的点数,回答
(1)写出图中点数构成的数列 的一个递推公式;并根据这个递推公式,求出数列 的通项公式;
(2)若 是数列 的前 项和,证明: .
18.(本小题满分12分)已知函数 ,其中 , ,函数 图象上相邻
的两条对称轴之间的距离为 .
(1)求 的解析式和单调递增区间;
(2)若将函数 图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再向右平移 个单位长度,
得到函数 的图象,求函数 在 上的最大值.
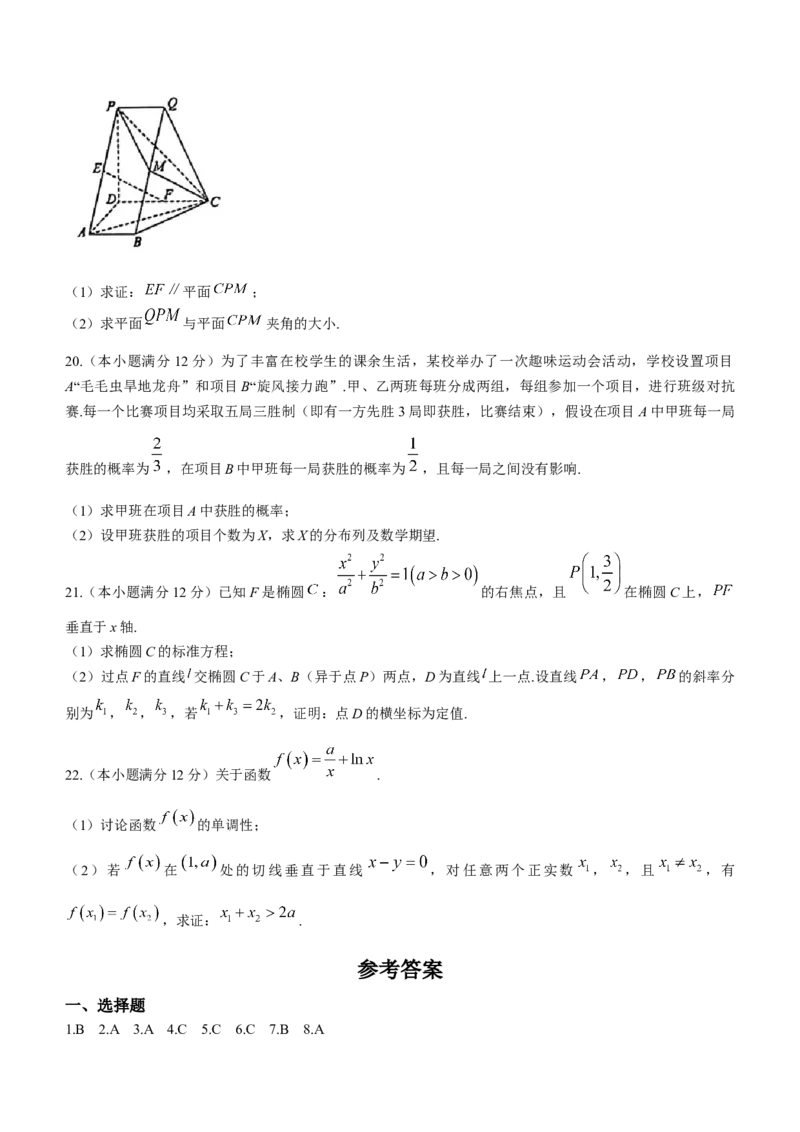
19. ( 本 小 题 满 分 12 分 ) 如 图 , 平 面 , , , ,
,点E,F,M分别为 , , 的中点.
学科网(北京)股份有限公司(1)求证: 平面 ;
(2)求平面 与平面 夹角的大小.
20.(本小题满分12分)为了丰富在校学生的课余生活,某校举办了一次趣味运动会活动,学校设置项目
A“毛毛虫旱地龙舟”和项目B“旋风接力跑”.甲、乙两班每班分成两组,每组参加一个项目,进行班级对抗
赛.每一个比赛项目均采取五局三胜制(即有一方先胜3局即获胜,比赛结束),假设在项目A中甲班每一局
获胜的概率为 ,在项目B中甲班每一局获胜的概率为 ,且每一局之间没有影响.
(1)求甲班在项目A中获胜的概率;
(2)设甲班获胜的项目个数为X,求X的分布列及数学期望.
21.(本小题满分12分)已知F是椭圆 : 的右焦点,且 在椭圆C上,
垂直于x轴.
(1)求椭圆C的标准方程;
(2)过点F的直线 交椭圆C于A、B(异于点P)两点,D为直线 上一点.设直线 , , 的斜率分
别为 , , ,若 ,证明:点D的横坐标为定值.
22.(本小题满分12分)关于函数 .
(1)讨论函数 的单调性;
(2)若 在 处的切线垂直于直线 ,对任意两个正实数 , ,且 ,有
,求证: .
参考答案
一、选择题
1.B 2.A 3.A 4.C 5.C 6.C 7.B 8.A
学科网(北京)股份有限公司二、多选题
9.CD 10.ABD 11.ACD 12.ABD
三、填空题
13.-192 14. 15. 16.
四、解答题
17.(1)
(2)(方法:裂项相消)证明省略
18.(1)
(2)
19.(1)证明四边形 为平行四边形即可
(2)面面角的大小为60°
20.(1)64/81
(2)209/162
21.(1)
(2)
22.(1)分类讨论 的情况即可
(2)构造函数即可证明.
学科网(北京)股份有限公司