文档内容
机密★启用前 〔考试时间:2024年7月3日下午15∶00-17∶00〕
乐山市高中 2025届期末教学质量检测
数 学
(考试时间:120分钟 试卷总分:150分)
注意事项:
1.答题前先将自己的姓名、准考证号、考场号、座位号填写在试卷和答题卡上,认真
核准准考证号条形码上的以上信息,将条形码粘贴在答题卡上的指定位置.
2.请按题号顺序在答题卡上各题目的答题区域内作答,写在试卷、草稿纸和答题卡的
非答题区域均无效.
3.选择题用 2B铅笔在答题卡上把所选答案的标号涂黑;非选择题用黑色签字笔在答
题卡上作答;字体工整,笔迹清楚.
4.考试结束后,请将试卷和答题卡一并交回.
一、单项选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一
项是符合题目要求的.
1
1.已知函数f(x)=x2,则f′(4)=
1 1
A. B. C.1 D.2
4 2
2.已知数列1,槡3,槡5,槡7,3,…,按此规律,3槡3是该数列的
A.第11项 B.第12项 C.第13项 D.第14项
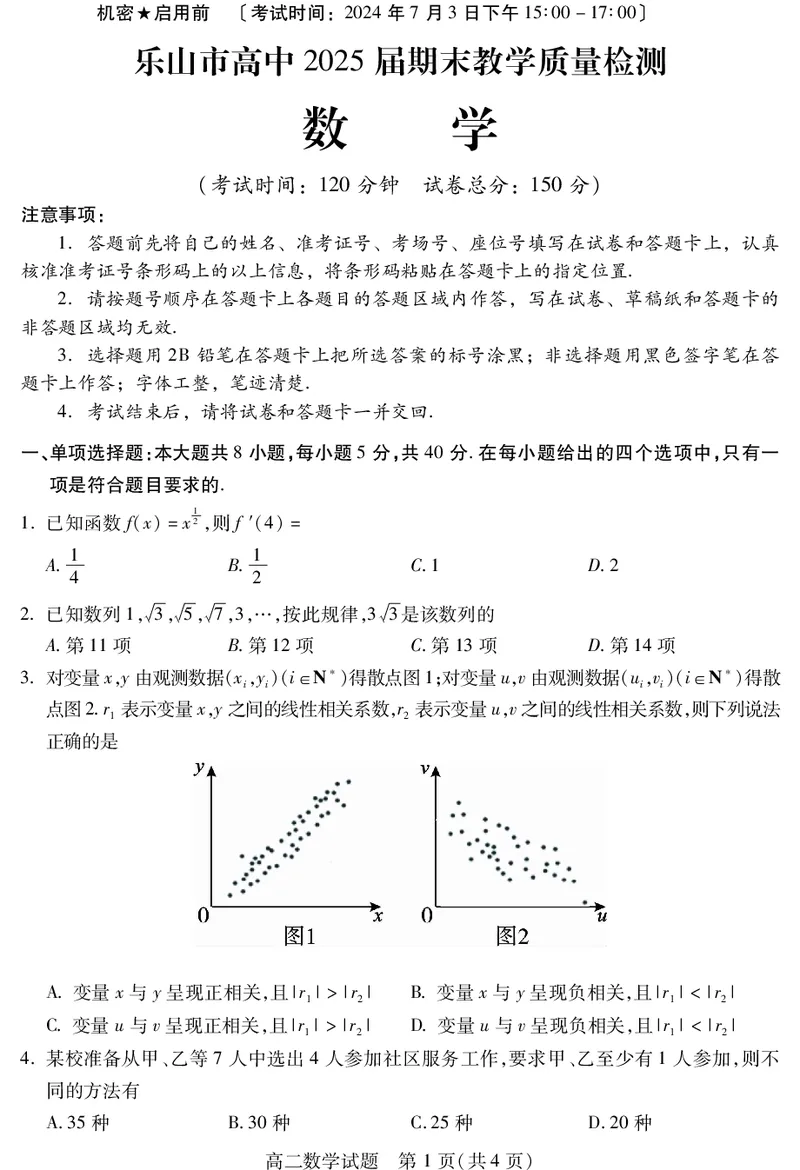
3.对变量x,y由观测数据(x,y)(i∈N)得散点图1;对变量u,v由观测数据(u,v)(i∈N)得散
i i i i
点图2.r表示变量x,y之间的线性相关系数,r表示变量u,v之间的线性相关系数,则下列说法
1 2
正确的是
A变量x与y呈现正相关,且|r|>|r| B变量x与y呈现负相关,且|r|<|r|
1 2 1 2
C变量u与v呈现正相关,且|r|>|r| D变量u与v呈现负相关,且|r|<|r|
1 2 1 2
4.某校准备从甲、乙等7人中选出4人参加社区服务工作,要求甲、乙至少有1人参加,则不
同的方法有
A.35种 B.30种 C.25种 D.20种
高二数学试题 第 1页(共4页)
{{##{{QQQQAABBbYYYASEtwgggiAQAgAJSIAAACAYQ5gqCQQQQWGOaCCwgiOQQkIkEAgGJUACgEQxgVOCQOFKAAMxsqAwAYANwAQBNAAA=B}A#A}=}#}
书书书5.牛顿在《流数法》一书中,给出了高次代数方程的一种数值解法———牛顿法.设 r是 f(x)=
x2+x-1=0(x>0)的根,选取x=1作为r的初始近似值,过点(x,f(x))做曲线y=f(x)
0 0 0
的切线l,l与x轴的交点的横坐标为 x,称 x是 r的一次近似值;过点(x,f(x))做曲线
1 1 1 1
y=f(x)的切线,则该切线与x轴的交点的横坐标为x,称x是r的二次近似值.则x=
2 2 2
2 11 13 17
A. B. C. D.
3 20 21 27
6.某市组织5名志愿者到当地三个学校开展活动,要求每个学校至少派一名志愿者,每名志
愿者只能去一个学校,则不同的派出方法有
A.240种 B.150种 C.120种 D.60种
7.某次大型联考有10000名学生参加,考试成绩(满分100分)近似服从正态分布 X~N(μ,
σ2)(其中μ和σ分别为样本的均值和标准差),若本次考试平均成绩为65分,87分以上共
有228人,学生甲的成绩为76分,则学生甲的名次大致是( )名.
附:若随机变量X服从正态分布N(μ,σ2),则P(μ-σ<X≤μ+σ)≈0.6827,
P(μ-2σ<X≤μ+2σ)≈0.9545,P(μ-3σ<X≤μ+3σ)≈0.9937.
A.456 B.1587 C.3174 D.8413
{ 1 }
8.已知数列{a}的前n项和S=n2,记数列 的前n项和为T,则T =
n n aa n 2024
n n+1
4047 2023 4048 2024
A. B. C. D.
4048 4048 4049 4049
二、多项选择题:本大题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合
题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
2 1
9.设离散型随机变量X满足P(X=i)=Ci( )i( )5-i(i=0,1,2,3,4,5),则下列说法正确的是
5 3 3
80 10 5
AP(X=3)= BE(X)= CD(X)= DE(3X+1)=11
243 3 3
10.已知等差数列{a}的公差为d,前n项和为S,若a+a=-8,a+a=-12,则下列说法
n n 2 5 1 4
正确的是
Ad=-2 Ba=2n-11 CS =0 DS最小值为-25
n 10 n
11.若(1+x)2024(1-x)2024=a+ax+ax2+…+a x4048,则
0 1 2 4048
Aa=0 Ba =C1012
0 2024 2024
2024 4048
C∑a =0 D∑(ia2i-1)=4048×32023
2i i
i=0 i=1
3n-1
12.在数列{a}中,a=1,a -a=2n,若不等式2+λ·(-1)n≥ 对任意 n∈N恒成
n 1 n+1 n a+1
n
立,则实数λ的值可以是
A.1 B.0 C.-1 D.-2
高二数学试题 第 2页(共4页)
{{##{{QQQQAABBbYYYASEtwgggiAQAgAJSIAAACAYQ5gqCQQQQWGOaCCwgiOQQkIkEAgGJUACgEQxgVOCQOFKAAMxsqAwAYANwAQBNAAA=B}A#A}=}#}三、填空题:本大题共4小题,每小题5分,共20分.
13.由数字2,3,4,5可组成 个三位数 (各位上数字可重复,用数字作答).
14.一个不透明的箱子中有5个小球,其中2个白球,3个黑球,现从中任取两个小球,其中一
个是白球,则另一个也是白球的概率是 .
1 1 1 1 1
15.数列{a}是各项均为正数的等比数列,满足a+a=8( + ),a+a+a=256( + + ),则
n 1 2 a a 3 4 5 a a a
1 2 3 4 5
数列的通项a= .
n
ex-1 1
16.已知函数f(x)=ae1-x- +x- ,若f(x)≥0有解,则a的取值范围是 .
a x
四、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或推演步骤.
17.(本小题10分)
某游泳俱乐部为了解中学生对游泳是否有兴趣,从某中学随机抽取男生和女生各50人进
4
行调查,对游泳有兴趣的人数占总人数的 ,女生中有5人对游泳没有兴趣.
5
(1)完成下面2×2列联表:
有兴趣 没有兴趣 合 计
男
女
合 计
(2)依据a=0.05的独立性检验,能否认为游泳兴趣跟性别有关?
n(ad-bc)2
附:χ2= ,其中n=a+b+c+d.
(a+b)(c+d)(a+c)(b+d)
α 0.10 0.05 0.01 0.005
χ 2.706 3.841 6.635 7.879
a
18.(本小题12分)
已知函数f(x)=x(x-c)2.
(1)若c=2,求函数y=f(x)在(1,f(1))处的切线方程;
(2)讨论函数y=f(x)的单调性.
19.(本小题12分)
2020年至2023年全国粮食年产量y(单位:万万吨)的数据如下表:
年份 2020 2021 2022 2023
年份代号x 1 2 3 4
总产量y 6.69 6.82 6.86 6.95
高二数学试题 第 3页(共4页)
{{##{{QQQQAABBbYYYASEtwgggiAQAgAJSIAAACAYQ5gqCQQQQWGOaCCwgiOQQkIkEAgGJUACgEQxgVOCQOFKAAMxsqAwAYANwAQBNAAA=B}A#A}=}#}(1)请用相关系数判断y关于x的线性相关程度(计算时精确到小数点后2位,若|r|>0.75,
则线性相关程度较高,若0.3<|r|<0.75,则线性相关程度一般);
(2)求出y关于x的线性回归方程,并预测2025年全国粮食年产量.
n
∑(x-x珋)(y-y珋)
i i
参考公式:相关系数r= i=1 ,回归直线方程的斜率
n n
槡∑(x-x珋)2槡∑(y-y珋)2
i i
i=1 i=1
n n
∑(x-x珋)(y-y珋) ∑xy-nx珋·y珋
i i ii
b^=i=1 =i=1 ,截距a^=y珋-b^x珋.
n n
∑(x-x珋)2 ∑x2-nx珋2
i i
i=1 i=1
4 4
参考数据:∑xy=68.71,槡∑(y-y珋)2≈0.19,槡5≈2.24.
ii i
i=1 i=1
20.(本小题12分)
设数列{a}是等差数列,{b}是等比数列,且a=b=1,a+b=8,2a-b=-3.
n n 1 1 3 2 2 3
(1)求数列{a},{b}的通项公式;
n n
a
(2)若数列{b}单调递增,记c= n,求数列{c}的前n项和T,并证明:1≤T<3.
n n b n n n
n
21.(本小题12分)
某校篮球队举行投篮与传球训练:
(1)投篮规则如下:每名队员用一组篮球定点投篮,一组3个球,先投2个普通球,再投1个花
1
球.记投进一个普通球得1分,普通球投进的概率为 ;投进一个花球得2分,花球投进的
2
1
概率为 .记某队员进行一组定点投篮训练后得分为X,求X的分布列和期望E(X);
4
(2)现选投篮成绩最好的3名队员进行传球展示,从甲开始,每次等可能地传给另外两名
队员,接到球的队员又等可能地传给另外两名队员,如此反复,假设传出的球都能接
住.求传了n次球后,球在甲手上的概率p.
n
22.(本小题12分)
已知函数f(x)=(ex+a)x,g(x)=(x+a)lnx.
(1)当a=0时,求函数y=f(x)的极值;
1 1
(2)当a≥ 时,若f(x)=g(x)=t(t>0),求证:x(x+1)lnt≥- .
e2 1 2 1 2 e
高二数学试题 第 4页(共4页)
{{##{{QQQQAABBbYYYASEtwgggiAQAgAJSIAAACAYQ5gqCQQQQWGOaCCwgiOQQkIkEAgGJUACgEQxgVOCQOFKAAMxsqAwAYANwAQBNAAA=B}A#A}=}#}