文档内容
2025
内部
新高考数学
圆锥曲线黄金55题
精研好题,跳出题海
适合110分以上
公众号:邦达数学圆锥曲线黄金55题
【建议110分以上使用】
单选题(共10小题)
x2 y2
1 已知双曲线C: - =1(a>0,b>0)的左、右焦点分别为F,F,M,N为双曲线一条渐
a2 b2 1 2
2π
近线上的两点,A为双曲线的右顶点,若四边形MFNF 为矩形,且∠MAN= ,则双曲线C的
1 2 3
离心率为 ( )
21
A. 3 B. 7 C. D. 13
3
解析:如图,因为四边形MFNF 为矩形,所以|MN|=|FF|=2c(矩形的对角线相等),
1 2 1 2
所以以MN为直径的圆的方程为x2+y2=c2,
b
直线MN为双曲线的一条渐近线,不妨设其方程为y= x,
a
b
由 y= a x ,解得 x=a ,或 x=-a ,
y=b y=-b
x2+y2=c2
所以N(a,b),M(-a,-b)或N(-a,-b),M(a,b),
不妨设N(a,b),M(-a,-b),又A(a,0)
所以|AM|= (a+a)2+b2= 4a2+b2,|AN|= (a-a)2+b2=b,
2π
在△AMN中,∠MAN= ,
3
2π
由余弦定理得|MN|2=|AM|2+|AN|2-2|AM||AN|•cos ,
3
即4c2=4a2+b2+b2+ 4a2+b2×b,则2b= 4a2+b2,
4
所以4b2=4a2+b2,则b2= a2,
3
b2 21
所以e= 1+ = .故选:C.
a2 3
圆锥曲线黄金55题 12 已知F为抛物线y2=2px的焦点,过F的直线l与抛物线交于A,B两点,以AF、BF为直径
的圆分别与x轴交于异于F的M,N两点,且MF=2FN,则直线l的斜率为 ( )
1 1
A. B. 2 2 C. ± D. ±2 2
3 3
解析:如图所示,
p
设O 为AF的中点,O 为BF的中点,A(x,y)B(x ,y ),F ,0
2 1 1 1 2 2 2
2 公众号:邦达数学
,
p
+x
所以O 2 1 , y 1
2 2 2
p
x +
,O 2 2 , y 2
1 2 2
,作OP⊥x轴于P,O Q⊥x轴于Q,
1 2
p
x +
则P
2 2
,0
2
p
+x
,Q
2 1
,0
2
,因为ON=OF,
1 1
所以P为NF的中点,则FN =2FP,同理,MF=2QF,因为MF=2FN,
p
所以2Q
F
=2•2F
P
,即Q
F
=2F
P
,即
p
-
2 +x 1
,0
2 2
p
x +
=2
2 2
-
p
,0
2 2
,
p
+x
p 2 1 p 3p
所以 - =x + -p,整理得x +2x = ,(*)
2 2 2 2 1 2 2
p
设直线l的方程为y=kx-
2
,
p
y=kx-
联立 2
p2k2
,消y整理得k2x2-(pk2+2p)x+ =0,
4
y2=2px
pk2+2p p2
所以x +x = ,xx = ,
1 2 k2 1 2 4
p 2p p 4p p2
结合(*)式可得x = - ,x = + ,代入xx = 中,
2 2 k2 1 2 k2 1 2 4
p 2p
即 -
2 k2
p 4p
+
2 k2
p2 1 2
= ,因为p≠0,所以 -
4 2 k2
1 4
+
2 k2
1
= ,
4
即k2=8,所以k=±2 2,故选:D.3 已知直线l:2kx-2y-kp=0与抛物线C:y2=2px(p>0)相交于A,B两点,点M(-1,-1)
是抛物线C的准线与以AB为直径的圆的公共点,则下列结论错误的是 ( )
A. p=2 B. k=-2
C. △MAB的面积为5 5 D. |AB|=5
p p
解析:由点M(-1,-1)为准线x=- 上的一点,可得- =-1,解得p=2,
2 2
∴抛物线C:y2=4x,
∴直线l:2kx-2y-kp=0化为:y=k(x-1),直线l经过抛物线C的焦点F(1,0),
设A(x,y),B(x ,y ),
1 1 2 2
x +x +p x +x +p
则以AB为直径的圆的半径R= 1 2 ,因此线段AB的中点到准线的距离= 1 2 ,
2 2
∴以AB为直径的圆与准线相切点M,圆心为G(x ,-1).
0
由y2=4x,y2=4x ,相减可得:k×(-2)=4,解得k=-2.
1 1 2 2
∴直线l的方程为:y=-2(x-1),把G(x ,-1)代入可得:-1=-2(x -1),
0 0
3
×2+2
3 2 5
解得x = ,∴R= = ,|AB|=5,
0 2 2 2
|-2-1-2|
点M到直线l的距离d= = 5,
22+12
1 1 5 5
S = |AB|•d= ×5× 5= ,
△MAB 2 2 2
综上可得:ABD正确,C错误.
故选:C.
圆锥曲线黄金55题 34 已知抛物线y2=2x的焦点为F,准线为l,圆C经过点F并与抛物线相交于点M,若|MF|=
5
,且圆C与l相切,则这样的圆一共有( )个.
2
A. 1 B. 2 C. 3 D. 4
1
解析:抛物线y2=2x的焦点为F ,0
2
4 公众号:邦达数学
1
,准线为l:x=- ,
2
5 1
因为|MF|= =x + ,x =2,所以点M的坐标为(2,2)或(2,-2),
2 M 2 M
圆心C在FM的中垂线上,且|CF|等于点C到l的距离,
因此点C只能在抛物线上,问题转换为中垂线与抛物线的交点个数,共有4个.
故选:D.5 已知抛物线y2=2px(p>0)的焦点为F,过点F的直线l交抛物线于A,B两点,若|AF|,
|AB|
,|FB|成等比数列,则线段AB在y轴上的射影长为 ( )
4
A. p B. 2p C. 3p D. 4p
p
解析:设直线l的倾斜角为θ(θ≠0),因为p+|AF|cosθ=|AF|,所以|AF|= ,
1-cosθ
同理可得|BF|+|BF|cosθ=p,
p
所以|BF|= ,
1+cosθ
p p p2
所以|AF|⋅|BF|= ⋅ = ,
1-cosθ 1+cosθ sin2θ
又|AB|=|AF|+|BF|,
p p 2p
所以|AB|= + = ,
1-cosθ 1+cosθ sin2θ
|AB| |AB|2
因为|AF|, ,|BF|成等比数列,所以得 =|AF|⋅|BF|,
4 16
所以|AB|2=16|AF|•|BF|,
4p2 p2 1
所以 =16 ,即sin2θ= ,
sin2θ sin2θ 4
1 1
所以sinθ= 或sinθ=- (舍),
2 2
因为线段AB在y轴上的射影长为|AB|sinθ,
2p 2p
即|AB|sinθ= sinθ= =4p,
sin2θ sinθ
故选:D.
圆锥曲线黄金55题 5x2 y2
6 已知F、F 分别是双曲线C: - =1(a>0,b>0)的左、右焦点,过点F 向一条渐近线
1 2 a2 b2 1
作垂线,交双曲线右支于点P,直线FP与y轴交于点Q(P,Q在轴同侧),连接QF,若△PQF 的
2 1 1
内切圆圆心恰好落在以FF 为直径的圆上,则双曲线的离心率为 ( )
1 2
A. 3 B. 2 C. 5 D. 2
b
解析:设由F 向渐近线y=- x所作垂线的垂足为M,△PQF 的内心为I,
1 a 1
由于|QF|=|QF|,所以内心I在y轴上.
1 2
又内心I在以线段F,F 为直径的圆上,
1 2
所以|OF|=|OF|=c,连接IF.IF,
1 2 1 2
则∠IFO=∠IFO=45°,设∠QFI=∠QFI=α,
1 2 1 2
则∠IFP=∠QFI=α,因此∠PFF =45°-α,
1 1 1 2
而∠PFF =∠QFI+∠IFO=45°+α,
2 1 2 2
因此∠PFF +∠PFF =45°-α+45°+α=90°,故∠FPF =90°.
1 2 2 1 1 2
又FM⊥OM,所以OM∥PF,所以M为PF的中点,易求得|OM|=a,
1 2
于是|PF|=2a.由双曲线定义可得|PF|=2a+2a=4a,
2 1
在Rt△PFF 中,由勾股定理可得(4a)2+(2a)2=(2c)2,
1 2
于是c2=5a2,故得双曲线的离心率e= 5.
故选:C.
6 公众号:邦达数学x2 y2
7 已知椭圆C: + =1的左、右顶点分别为A,B,F为椭圆C的右焦点,圆x2+y2=9上
9 8
有一动点P,P不同于A,B两点,直线PA与椭圆C交于点Q,k ,k 分别为直线BP,QF的斜
1 2
k
率则 1 的取值范围是 ( )
k
2
9
A. -∞,
8
圆锥曲线黄金55题 7
B. (-∞,-1)∪(-1,0)
3
C. -∞,
4
3
D. (-∞,0)∪0,
4
x2 y2
解析:椭圆C: + =1的焦点在x轴上,a=3,b=2 2,c=1,右焦点F(1,0),
9 8
由P在圆x2+y2=9上,则PA⊥PB,
1
-
1 k k 1
则k •k =-1,则k =- , 1 = AP =- ,
AP 1 1 k k k k k
AP 2 2 AP 2
2 2sinθ 2 2sinθ
设Q(3cosθ,2 2sinθ),则k •k = •
AP 2 3cosθ+3 3cosθ-1
8sin2θ 8-8cos2θ
= =
9cos2θ+6cosθ-3 9cos2θ+6cosθ-3
设t=cosθ,t∈(-1,1),
8-8t2
则k •k = ,
AP 2 9t2+6t-3
k 9t2+6t-3 9 3
∴ 1 = = + ,
k 8t2-8 8 4(t-1)
2
∵t∈(-1,1),
∴t-1∈(-2,0),
1 1
∈-∞,-
t-1 2
,
k 3
∴ 1 ∈-∞,
k 4
2
,且不等于0.
故选:D.1 1
8 关于曲线M:x2 +y2 =1,有下述两个结论:①曲线M上的点到坐标原点的距离最小值是
2 1
;②曲线M与坐标轴围成的图形的面积不大于 ,则下列说法正确的是 ( )
2 2
A. ①、②都正确 B. ①正确②错误 C. ①错误②正确 D. ①、②都错误
解析:对于①设曲线上的点为(x,y),
1 1
由x2 +y2 =1,可知x≥0,y≥0,x•y≠0,平方可得,x+y+2 xy=1.
1
∵x+y≥2 xy,∴x+y≥ .
2
2 2 1
又∵ x2+y2≥ (x+y)≥ ,当且仅当x=y= 时等号成立,故错误;
2 4 4
1 1 1 1
对于②,由x2 +y2 =1知,x,y∈[0,1],y2 =1-x2,两边平方可得y=1+x-2 x.
∵x≤ x,∴y=1+x-2 x≤1-x,即曲线C在直线y=1-x的下方,因此所围图形的面积不
1
大于 ,故正确.
2
故选:C.
8 公众号:邦达数学x2 y2
9 已知圆C :x2+y2=b2和椭圆C : + =1(a>b>0).直线y=kx与圆C 交于A、A
1 2 a2 b2 1 1
|OB|
两点,与椭圆C 交于B、B 两点.若k∈R时, 的取值范围是(1,2],则椭圆C 的离心率
2 1 |OA| 2
为 ( )
1 2 3 3
A. B. C. D.
2 2 2 4
解析:因为直线直线y=kx过原点,且与圆C 交于A、A 两点,
1 1
故|OA|=b,
y=kx
联立 x2 y2 ,消去y得(a2k2+b2)x2-a2b2=0,
+ =1
a2 b2
-a2b2
则x +x =0,x x = ,
B B1 B B1 a2k2+b2
a2b2
所以x2= ,
B a2k2+b2
x2
所以|OB|= x2+y2 = x2+b21- B
B B B a2
圆锥曲线黄金55题 9
c2 c2b2 c2
= x2+b2= +b2=b +1=
a2 B a2k2+b2 a2k2+b2
c2+b2+a2k2 a2(k2+1) k2+1
b =b =ab ,
a2k2+b2 a2k2+b2 a2k2+b2
|OB| k2+1
故 =a ,
|OA| a2k2+b2
令t=k2+1,(t≥1),
|OB| t 1
则 =a =a ,
|OA| a2t-c2 c2
a2-
t
c2
t≥1时,a2- ∈[b2,a2),
t
|OB| a
则 ∈1,
|OA| b
=(1,2],
a
所以 =2,即a=2b,所以c= 3b,
b
c 3
所以离心率e= = ,
a 2
故选:C.x2 y2
10 设椭圆C: + =1(a>b>0)的左,右顶点为A,B.P是椭圆上不同于A,B的一点,
a2 b2
a 2
设直线AP,BP的斜率分别为m,n,则当 3-
b 3mn
10 公众号:邦达数学
2
+ +3(ln|m|+ln|n|)取得最小值
mn
时,椭圆C的离心率为 ( )
1 2 4 3
A. B. C. D.
5 2 5 2
b2(a2-x2)
解析:A(-a,0),B(a,0),设P(x ,y ),则y2= 0 ,
0 0 0 a2
y y
则m= 0 ,n= 0 ,
x +a x -a
0 0
y2 b2
∴mn= 0 =- ,
x2-a2 a2
0
a 2
∴ 3-
b 3mn
2
+ +3(ln|m|+ln|n|)
mn
a 2
= 3-
b 3b2
-
a2
2 b 2 a
+ +6ln =
b2 a 3 b
-
a2
3 a
-2
b
2 a
+3
b
b
+6ln ,
a
a 2
令 =t>1,则f(t)= t3-2t2+3t-6lnt.
b 3
2t3-4t2+3t-6 (t-2)(2t2+3)
f′(t)= = ,
t t
∴当t=2时,函数f(t)取得最小值f(2).
a
∴ =2.
b
b
∴e= 1-
a
2 3
= ,
2
故选:D.多选题(共15小题)
11 已知抛物线C:y2=2px,C的准线与x轴交于K,过焦点F的直线l与C交于A,B两点,连
接AK、BK,设AB的中点为P,过P作AB的垂线交x轴于Q,下列结论正确的是 ( )
A. |AF|•|BK|=|AK|•|BF| B. tan∠AKF=cos∠PQF
p2
C. △AKB的面积最小值为 D. |AB|=2|FQ|
2
解析:设直线AB的倾斜角为α,即∠AFx=α,设A(x,y),B(x ,y ),P(x ,y ),
1 1 2 2 0 0
p
p x=my+
对于A选项:设直线AB为x=my+ ,联立直线AB与抛物线方程 2 ,
2
y2=2px
p
化简整理可得,y2-2pmy-p2=0,由韦达定理可得,y +y =2pm,yy =-p2,∵K- ,0
1 2 1 2 2
圆锥曲线黄金55题 11
,
y y y y 2myy +p(y +y )
∴ k + k = 1 + 2 = 1 + 2 = 1 2 1 2 =
AK BK p p my +p my +p (my +p)(my +p)
x + x + 1 2 1 2
1 2 2 2
-2mp2+2p2m
=0,∴x轴为∠AKB的角平分线,
(my +p)(my +p)
1 2
|AF| |AK|
∴根据角平分线的性质可得, = ,即|AF|•|BK|=|AK|•|BF|,故A正确,
|BF| |BK|
对于B选项:过A作AD⊥x轴,垂足为D,
y π
则tan∠AKF= 1 ,cos∠PQF=cos -α
p 2
x +
1 2
y y
=sinα= 1 = 1 ,
|AF| p
x +
1 2
所以tan∠AKF=cos∠PQF,故B正确;
1 p p
对于C选项:S =S +S = |KF||y -y |= |y -y |≥ ⋅2p=p2,
△AKB △AKF △BKF 2 1 2 2 1 2 2
当|y -y |=|AB|=2p,即AB⊥x时,取等号,故△AKB的面积最小值p2,故C错误;
1 2
y2=2px
1 1
对于D选项:
y2=2px
,两式相减(y
1
+y
2
)(y
1
-y
2
)=2p(x
1
-x
2
),
2 2
y -y 2p p y
tan= 1 2 = = ,所以PQ方程为y-y =- 0 (x-x ),
x -x y +y y 0 p 0
1 2 1 2 0
y p p
令y=0,-y =- 0 (x-x ),则x=p+x ,所以Q(p+x ,0),所以|FQ|=p+x - = +x ,
0 p 0 0 0 0 2 2 0
所以|AB|=x +x +p=2x +p=2|FQ|,故D正确;故选:ABD.
1 2 012 设F为抛物线C:y2=2px(p>0)的焦点,过点F的直线l与抛物线C交于A(x ,y )B(x ,
1 1 2
y )两点,过B作与x轴平行的直线,和过点F且与AB垂直的直线交于点N,AN与x轴交于点
2
M,则 ( )
A. xx +yy 为定值
1 2 1 2
B. 当直线l的斜率为1时,△OAB的面积为 2P(其中O为坐标原点)
C. 若Q为C的准线上任意一点,则直线QA,QF,QB的斜率成等差数列
p
D. 点M到直线FN的距离为
2
p
解析:A.F ,0
2
12 公众号:邦达数学
y2=2px
p
,设直线l的方程为ty=x- ,联立 p ,化为y2-2pty-p2=0,
2 ty=x-
2
p2
∴yy =-p2,y +y =2pt,∵4p2xx =(yy )2=p4,∴xx = ,
1 2 1 2 1 2 1 2 1 2 4
3
∴xx +yy =- p2为定值,因此A正确.
1 2 1 2 4
p
B.当直线l的斜率为1时,直线l的方程为y=x- ,
2
p2
代入椭圆方程可得:x2-3px+ =0,∴x +x =3p,∴|AB|=x +x +p=4p,
4 1 2 1 2
p
2 2p
点O到直线l的距离d= = ,
2 4
1 2p 2
∴△OAB的面积为 ×4p× = p2,因此B不正确.
2 4 2
p
C.设 Q- ,m
2
m m y -m
,则 k = =- ,k = 1
QF p p p QA p
- - x --
2 2 1 2
2py -2pm
= 1 ,k =
y2+p2 QB
1
2py -2pm 2m 2py -2pm 2py -2pm
2 ,∴2k -k -k =- - 1 - 2 ,
y2+p2 QF QA QB p y2+p2 y2+p2
2 1 2
通分后分子=-2[m(y2+p2)(y2+p2)+p(py -pm)(y2+p2)+p(py -pm)(y2+p2)]
1 2 1 2 2 1
=-2[mp4+mp2(y2+y2)+mp4+p2(yy2+y p2-my2-mp2)+p2(y2y +y p2-my2-mp2)]
1 2 1 2 1 2 1 2 2 1
=0,则直线QA,QF,QB的斜率成等差数列,因此C正确.
|AM| y |AN| y -y
D.如图所示,过点M作MH⊥FN,垂足为H,∵ = 1 ,∴ = 1 2 ,
|MN| -y |MN| -y
2 2
p
y x +
|AN| |AF| |AF| y -y 2 1 2
又 = ,∴ = 1 2 ,∴|MH|=
|MN| |MH| |MH| -y
2
y2 p
y 1 +
2 2p 2
=
y -y
2 1
py -p2y
2 + 1
2 2p
=
y -y y -y
2 1 2 1
p
= ,因此D正确.
2
故选:ACD.x2 y2
13 已知曲线C: - =1(m≠0) ( )
4 m
A. 若曲线C表示椭圆,则m<0且m≠-4
B. 若m=5时,以P(1,1)为中点的弦AB所在的直线方程为5x-4y-1=0
C. 当m<-4时,F,F 为曲线C的焦点,P为曲线C上一点,且PF ⊥PF,则△PFF 的面积等
1 2 1 2 1 2
于4
1 1 4
D. 若m>0时,直线l过曲线C的焦点F且与曲线相交于A,B两点,则 + =
|AF| |BF| m
解析:对于A,若曲线C表示椭圆,则m<0且m≠-4,故A正确;
x2 y2
对于B,若m=5时,联立直线5x-4y-1=0与椭圆 - =1方程可得4y2-8y+99=0,可
4 5
得Δ<0,可得直线AB与椭圆无交点,故错;
对于C,当m<-4时,曲线C表示焦点在y上的椭圆,
当PF ⊥PF 时∠FPF =90°,则△PFF 的面积等于S=b2tan45°=4,故正确;
1 2 1 2 1 2
对于D,若m>0时,直线l过曲线C的焦点F且与曲线相交于A,B两点,只有AB为焦点弦时
1 1 4
+ = ,故错.
|AF| |BF| m
故选:AC.
圆锥曲线黄金55题 13x2 y2
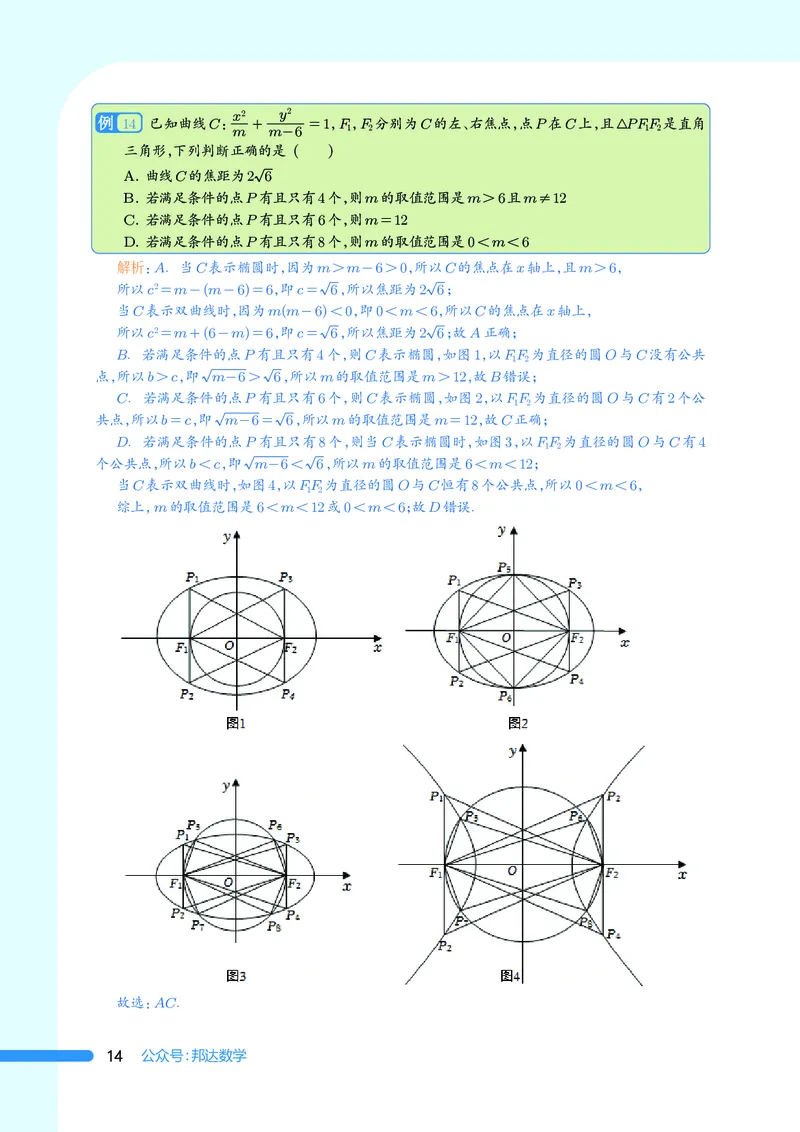
14 已知曲线C: + =1,F,F 分别为C的左、右焦点,点P在C上,且△PFF 是直角
m m-6 1 2 1 2
三角形,下列判断正确的是 ( )
A. 曲线C的焦距为2 6
B. 若满足条件的点P有且只有4个,则m的取值范围是m>6且m≠12
C. 若满足条件的点P有且只有6个,则m=12
D. 若满足条件的点P有且只有8个,则m的取值范围是0m-6>0,所以C的焦点在x轴上,且m>6,
所以c2=m-(m-6)=6,即c= 6,所以焦距为2 6;
当C表示双曲线时,因为m(m-6)<0,即0c,即 m-6> 6,所以m的取值范围是m>12,故B错误;
C.若满足条件的点P有且只有6个,则C表示椭圆,如图2,以FF 为直径的圆O与C有2个公
1 2
共点,所以b=c,即 m-6= 6,所以m的取值范围是m=12,故C正确;
D.若满足条件的点P有且只有8个,则当C表示椭圆时,如图3,以FF 为直径的圆O与C有4
1 2
个公共点,所以bb>0)中,其所有外切矩形的顶点在一个定圆Γ:x2+y2=a2+
a2 b2
b2上,称此圆为该椭圆的蒙日圆.该圆由法国数学家G•Monge(1746-1818)最先发现.若椭圆
x2 y2
C: + =1,则下列说法正确的有 ( )
16 9
A. 椭圆C外切矩形面积的最小值为48
B. 椭圆C外切矩形面积的最大值为48
C. 点P(x,y)为蒙日圆Γ上任意一点,点M(-10,0),N(0,10),当∠PMN取最大值时,
tan∠PMN=2+ 3
D. 若椭圆C的左、右焦点分别为F,F,过椭圆C上一点P和原点作直线l与蒙日圆相交于点
1 2
M,N,则PF•PF =PM•PN
1 2
解析:对于A.B.由题意可得:椭圆C外切矩形面积∈[4ab,2(a2+b2)],即为[48,50].因此A
正确,B不正确.
对于 C.当点 P 在第三象限,且 PM 与圆 Γ:x2+ y2= 25 相切时,∠PMN 取最大值,此时
r 5 3
tan∠OMP= = = ,锐角∠OMP=30°,∴∠PMN=45°+30°=75°,
102-r2 100-25 3
3
1+
tan45°+tan30° 3
∴tan∠PMN=tan(45°+30°)= = =2+ 3,因此C正确.
1-tan45°tan30° 3
1-
3
对于D.设|PF|=m,|PF|=n,设∠POF =α,则∠POF =π-α.在△POF 与△POF 中,分别
1 2 1 2 1 2
利用余弦定理可得:m2=c2+|OP|2-2c|OP|cosα,n2=c2+|OP|2-2c|OP|cos(π-α),
相加可得:m2+n2=2c2+2|OP|2,又m+n=2a,∴m2+n2+2mn=4a2,可得|PF|•|PF|=mn
1 2
=2a2-c2-|OP|2=a2+b2-|OP|2,又|PM|•|PN|=(|OM|-|OP|)(|OM|+|OP|)=|OM|2-|OP|2
=a2+b2-|OP|2,
∴|PF|•|PF|=|PM|•|PN|.因此D正确.
1 2
故选:ACD.
圆锥曲线黄金55题 153
16 已知抛物线C:y2=2px(p>0)的焦点为F,其准线与x轴交于点M- ,0
2
16 公众号:邦达数学
,过点F作不
垂直于x轴的直线l与C交于A,B两点.设P为x轴上一动点,Q为AB的中点,且AB⊥PQ,
则 ( )
27
A. 抛物线C的方程为y2=3x B. |AB|+3|BF|的最小值为
2
C. |AB|>2|PF| D. |BF|(|MA|+|MB|)=2|MB||PF|
3
解析:由抛物线C的准线与x轴交于点M- ,0
2
p 3
,得- =- ,所以p=3,所以抛物线C的方
2 2
程为y2=6x,A错误;
3
设直线l的方程为x=my+ ,A(x,y),B(x ,y ),
2 1 1 2 2
3
x=my+ ,
由 2 ,整理得y2-6my-9=0,则y
1
+y
2
=6m,y
1
y
2
=-9,
y2=6x
3 3
由抛物线的定义,知|AF|=x + =my +3,|BF|=x + =my +3,
1 2 1 2 2 2
1 1 1 1 my +3+my +3 m(y +y )+6
所以 + = + = 1 2 = 1 2 =
|AF| |BF| my +3 my +3 (my +3)(my +3) m2yy +3m(y +y )+9
1 2 1 2 1 2 1 2
6m2+6 2
= ,
-9m2+18m2+9 3
3 1 1
所以|AB|+3|BF|=|AF|+4|BF|= +
2 |AF| |BF|
3 4|BF| |AF|
(|AF|+4|BF|)= 5+ +
2 |AF| |BF|
3 4|BF| |AF|
≥ 5+2 ⋅
2 |AF| |BF|
27
= ,
2
当且仅当|AF|=2|BF|时取得等号,B正确;
3
由上可知,F ,0
2
,设点Q的坐标为(x ,y ),则2x =x +x ,2y =y +y .
0 0 0 1 2 0 1 2
由 y y 2 1 2 2 = = 6 6 x x 1 2 , , 得y2 1 -y2 2 =6(x 1 -x 2 ),所以 x y 1 1 - - y x 2 2 = y 1 + 6 y 2 = y 3 0 ,则直线l的斜率为 y 3 0 ,
y y
因为AB⊥PQ,所以直线PQ的斜率为- 0 ,则直线PQ的方程为y-y =- 0 (x-x ).
3 0 3 0
3 3
令y=0,则x=x +3,所以点P的坐标为(x +3,0),则|PF|=x +3- =x + .
0 0 0 2 0 2
由抛物线的定义可知,|AB|=|AF|+|BF|=x +x +3=2x +3,所以|AB|=2|PF|,C错误;
1 2 0
y y
因为k +k = 1 + 2
AM BM 3 3
x + x +
1 2 2 2
y y y(my +3)+y (my +3) 2myy +3(y +y )
= 1 + 2 = 1 2 2 1 = 1 2 1 2 =
my +3 my +3 (my +3)(my +3) m2yy +3m(y +y )+9
1 2 1 2 1 2 1 2
2m×(-9)+3×6m
=0,
m2yy +3m(y +y )+9
1 2 1 2
所以直线AM与直线BM关于x轴对称,即MF平分∠AMB,
|AM| |AF| |AM|+|BM| |AF|+|BF| |AB| 2|PF|
所以 = ,则 = = = ,
|BM| |BF| |BM| |BF| |BF| |BF|
整理得|BF|(|MA|+|MB|)=2|MB||PF|,D正确.
故选:BD.17 已知抛物线C:y2=2px(p>0)的焦点为F(1,0),坐标原点为O,直线l与抛物线C交于A,
B两点(与O均不重合),以线段AB为直径的圆过原点O,则△AOB与△AOF的面积之和能为
( )
A. 17 B. 8 5 C. 18 D. 9 3
解析:因为抛物线C:y2=2px(p>0)的焦点为F(1,0),
p
所以 =1,所以p=2,
2
所以抛物线C的方程为y2=4x,
若直线的斜率为0,则直线与抛物线有且只有一个交点,与条件矛盾,
所以直线的斜率不为0,所以可设直线的方程为x=my+t,
y2=4x
联立 可得y2-4my-4t=0,
x=my+t
由已知方程y2-4my-4t=0的判别式Δ=16m2+16t>0,
设A(x,y),B(x ,y ),则y +y =4m,yy =-4t,
1 1 2 2 1 2 1 2
因为以线段AB为直径的圆过原点O,所以OA⋅OB=0,
所以xx +yy =0,所以t2-4t=0,
1 2 1 2
所以t=4或t=0,
所以t=4,所以y +y =4m,yy =-16,
1 2 1 2
设直线与x轴的交点为D,则D(4,0),
1 1
△AOB的面积S =S +S = ×4×|y|+ ×4×|y |=2|y -y |,
△AOB △AOD △BOD 2 1 2 2 1 2
所以△AOB的面积S =2 (y +y )2-4yy =8 m2+4,
△AOB 1 2 1 2
1
△AOF的面积S = ×1×|y|.
△AOF 2 1
当y =2m+2 m2+4,则△AOB与△AOF的面积之和S=9 m2+4+m,
1
9m 5
又S′= +1,由S'=0可得m=- ,
m2+4 10
5 5
当m<- 时,S'<0,函数S=9 m2+4+m在-∞,-
10 10
圆锥曲线黄金55题 17
上单调递减,
5 5
当m>- 时,S'>0,函数S=9 m2+4+m在- ,+∞
10 10
上单调递增,
5
所以S≥8 5,当且仅当m=- 时等号成立;
10
当y =2m-2 m2+4,则△AOB与△AOF的面积之和S=9 m2+4-m,
1
9m 5
又S′= -1,由S′=0可得m= ,
m2+4 10
5 5
当m< 时,S'<0,函数S=9 m2+4-m在-∞,
10 10
上单调递减,
5 5
当m> 时,S'>0,函数S=9 m2+4-m在 ,+∞
10 10
上单调递增,
5
所以S≥8 5,当且仅当m= 时等号成立;
10
又8 5= 320> 289=17,8 5= 320> 243=9 3,8 5= 320< 324=18,
所以△AOB与△AOF的面积之和可能为18或8 5,
故选:BC.18 过抛物线C:y2=2px(p>0)焦点F的直线与C交于A,B两点,点A,B在C的准线l上的
射影分别为A,B,O为坐标原点,则 ( )
1 1
A. 以AB为直径的圆与准线l相切
B. △OAF可能为正三角形
1 1 2
C. + =
|AF| |BF| p
D. 记△AAF,△AFB,△FBB的面积分别为S,S ,S ,则S2=4SS
1 1 1 1 1 2 3 2 1 3
解析:对于A,如图,假设点A位于第四象限,根据抛物线的定义可得|AB|=|AF|+|BF|=|AA |
1
+|BB|,
1
设AB中点为G,点G在准线l上的射影为G,
1
|AA|+|BB| |AB|
所以|GG|= 1 1 = ,
1 2 2
所以以AB为直径的圆与准线相切,故A正确;
对于B,设AA 与y轴交于点M,若△OAF为正三角形,
1
p
则|AM|=|MA|,即x = ,
1 A 2
p
此时A ,-p
2
18 公众号:邦达数学
p
,|OA|=
2
2 5
+(-p)2= p≠|AA|=p,
2 1
所以此时△OAF不是正三角形,故B错误;
p
p x=my+
对于C,设直线AB:x=my+ ,联立 2 ,得y2-2pmx-p2=0,
2
y2=2px
则y +y =2pm,y y =-p2,
A B A B
pm p2 p2
x +x =m(y +y )+p=2pm2+p,x x =m2y y + (y +y )+ = ,
A B A B A B A B 2 A B 4 4
1 1 |AF|+|BF| x +x +p
所以 + = = A B
|AF| |BF| |AF||BF| p
x +
A 2
p
x +
B 2
x +x +p
= A B
p p2
x x + (x +x )+
A B 2 A B 4
2pm2+p+p 2(pm2+p) 2
= = = ,故C正确;
p2 p2 p2 p(pm2+p) p
+p2m2+ +
4 2 4
1 p
对于D,S =- x +
1 2 A 2
1 1 p
y ,S = ⋅p⋅(y -y ),S = x +
A 2 2 B A 3 2 B 2
y ,
B
4SS =-(my +p)(my +p)y y =-[m2y y +mp(y +y )+p2]y y =p2(m2p2+p2),
1 3 A B A B A B A B A B
1 1
S2= p2(y -y )2= p2[(y +y )2-4y y ]=p2(m2p2+p2),所以S2=4SS ,故D正确.
2 4 B A 4 B A A B 2 1 3
故选:ACD.y2
19 如图,过双曲线C:x2- =1(b>0)右支上一点P作双曲线的切线l分别交两渐近线于
b2
A、B两点,交x轴于点D,F,F 分别为双曲线的左、右焦点,O为坐标原点,则下列结论正确的
1 2
是 ( )
A. |AB| =2b
min
B. S =S
△OAP △OBP
C. S =2b
△AOB
1
D. 若存在点P,使cos∠FPF = ,且FD=2DF,则双曲线C的离心率e=2
1 2 4 1 2
解析:对于A,不妨设P在第一象限,且P(x ,y ).
0 0
y2 b2x
由x2- =1,得y= b2x2-b2,∴y′= ,
b2 b2x2-b2
b2x b2x
则在点P(x ,y )的切线斜率为k= 0 = 0 ,
0 0 b2x2 0 -b2 y 0
b2x
∴在点P(x ,y )的切线方程为:y-y = 0 (x-x ),
0 0 0 y 0
0
y2 y y
又∵x2- 0 =1,∴在点P(x ,y )的切线方程为:x x- 0 =1,
0 b2 0 0 0 b2
不失一般性,设点P(x ,y )是双曲线在第一象限的一点,A(x ,y )是切线与渐近线在第一象限的
0 0 1 1
交点,B(x ,y )是切线与渐近线在第四象限的交点,
2 2
双曲线的渐近线方程为y=±bx,
y y
联立 x 0 x- b 0 2 =1 ,解得点A b , b2
bx -y bx -y
y=bx 0 0 0 0
圆锥曲线黄金55题 19
,
b -b2
同理可得:B ,
bx +y bx +y
0 0 0 0
,
b b
则|AB|= -
bx -y bx +y
0 0 0 0
2 b2 b2
+ +
bx -y bx +y
0 0 0 0
2
=2 (b2+1)x2-1,
0
又∵x ≥1,∴|AB|≥2 (b2+1)-1=2b,即|AB| =2b,故A正确;
0 min
b b b2 -b2
+ +
bx -y bx +y bx -y bx +y
对于B,由A知, 0 0 0 0 =x , 0 0 0 0 =y ,
2 0 2 0
∴点P(x ,y )是A、B的中点,∴S =S ,故B正确;
0 0 △OAP △OBP
b2x
对于C,∵在点P(x ,y )的切线方程为:y-y = 0 (x-x ),
0 0 0 y 0
0
1 1
令y=0,得x= ,∴点D ,0
x x
0 0
,1 1 1 b2 b2
则S =S +S = ×|OD|×|y -y |= × × +
△AOB △AOD △BOD 2 1 2 2 x bx -y bx +y
0 0 0 0 0
20 公众号:邦达数学
=b,
当点P(x ,y )在顶点(1,0)时,仍然满足S =b,故C错误;
0 0 △AOB
1
对于D,∵F(-c,0),F(c,0),D ,0
1 2 x
0
,
1
∴FD= +c,0
1 x
0
1
,DF =c- ,0
2 x
0
,
1 1
又∵FD=2DF,∴ +c=2c-
1 2 x x
0 0
3 3
,解得c= ,即x = ,
x 0 c
0
y2 9b2
代入x2- 0 =1,得y2= -b2,
0 b2 0 c2
3
∴|PF|2=(x +c)2+y2= +c
1 0 0 c
2 9b2 9 9b2
+ -b2= +c2+6+ -b2
c2 c2 c2
9 9(c2-1) 3
= +c2+6+ -(c2-1)=16,|PF|2=(x -c)2+y2= -c
c2 c2 2 0 0 c
2 9b2 9
+ -b2= +c2
c2 c2
9b2
-6+ -b2
c2
9 9(c2-1)
= +c2-6+ -(c2-1)=4,
c2 c2
|PF|2+|PF|2-|FF|2 16+4-4c2 5-c2 1
∴cos∠FPF = 1 2 1 2 = = = ,
1 2 2×|PF|×|PF| 2×4×2 4 4
1 2
解得:c2=4,∴c=2,
c
则离心率为e= =2,故D正确.
a
故选:ABD.x2 y2
20 已知椭圆E: + =1,过椭圆E的左焦点F 的直线l 交E于A,B两点(点A在x轴的
4 3 1 1
上方),过椭圆E的右焦点F 的直线l 交E于C,D两点,则 ( )
2 2
6
A. 若AF =2FB,则l 的斜率k=
1 1 1 2
27
B. |AF|+4|BF|的最小值为
1 1 4
C. 以AF 为直径的圆与圆x2+y2=4相切
1
288
D. 若l ⊥l ,则四边形ADBC面积的最小值为
1 2 49
解析:易知:F(-1,0),F(1,0),
1 2
对于A,若AF =2FB,显然直线l 的斜率存在且大于0,
1 1 1
设直线l:y=k(x+1)(k>0),A(x,y),B(x ,y ),
1 1 1 2 2
y=k(x+1)
联立椭圆方程 x2 y2 ,化简整理得(4k2+3)x2+8k2x+4k2-12=0,
+ =1
4 3
-8k2 4k2-12
显然Δ>0,x +x = ,xx = ,
1 2 4k2+3 1 2 4k2+3
又AF =(-1-x,-y),FB=(x +1,y ),
1 1 1 1 2 2
故-1-x =2(x +1),整理得x +2x =-3,
1 2 1 2
x +x =
-8k2
1 2 4k2+3
5
由 x +2x =-3 ,解得k2= ,
1 2 4
4k2-12
xx =
1 2 4k2+3
5
又k>0,故k= ,A错误;
2
对于B,易知直线l 的斜率不为0,
1
设直线l:x=my-1,A(x,y),B(x ,y ),
1 1 1 2 2
x=my-1
联立椭圆方程 x2 y2 ,化简整理得(3m2+4)y2-6my-9=0,
+ =1
4 3
6m -9
显然Δ>0,y +y = ,yy = ,
1 2 3m2+4 1 2 3m2+4
由点A在x轴的上方,显然y >0,y <0,
1 2
又|AF|= (x +1)2+y2= 1+m2⋅y,|BF|= (x +1)2+y2=- 1+m2⋅y ,
1 1 1 1 1 2 2 2
1 1 1 1 y -y - [(y +y)2-4y ⋅y ]
+ = - = 2 1 = 2 1 1 2 =
|AF| |BF| 1+m2⋅y 1+m2⋅y 1+m2⋅y ⋅y 1+m2⋅y ⋅y
1 1 1 2 1 2 1 2
圆锥曲线黄金55题 2112(1+m2)
3m2+4 4
= ,
9(1+m2) 3
3m2+4
3 1 1
| AF | + 4 | BF | = +
1 1 4 |AF| |BF|
1 1
22 公众号:邦达数学
3 4|BF| |AF|
( | AF | + 4 | BF | ) = 5+ 1 + 1
1 1 4 |AF| |BF|
1 1
≥
3 4|BF| |AF|
5+2 1 ⋅ 1
4 |AF| |BF|
1 1
27
= ,
4
4|BF| |AF|
故当且仅当 1 = 1 ,即|AF|=2|BF|时取等,B正确;
AF| |BF| 1 1
1 1
对于C,设A(x,y),AF 的中点为P,
1 1 1
x -1 y
则P 1 , 1
2 2
,
(x -1)2 y2 |AF|
又|OP|= 1 + 1 = 2 ,
4 4 2
|AF| |AF| |AF|
由椭圆定义知: 2 + 1 =2,即|OP|=2- 1 ,
2 2 2
又x2+y2=4的圆心为O(0,0),半径为2,
故以AF 为直径的圆与圆x2+y2=4内切,C正确;
1
对于D,当直线l 的斜率存在时,
1
由 上 知 :| AB | = (x -x )2+(y -y )2 = 1+k2 ⋅ (x +x )2-4xx = 1+k2 ⋅
1 2 1 2 1 2 1 2
-8k2
4k2+3
2 4k2-12 12(k2+1)
-4⋅ = ,
4k2+3 4k2+3
1 12 - k
同理|CD|=
2 +1
1
4-
k
12(1+k2)
= ,
2 4+3k2
+3
1 1 12(k2+1) 12(1+k2) 72(1+k2)2
故四边形ADBC面积为S= |AB|⋅|CD|= ⋅ ⋅ = ,
2 2 4k2+3 4+3k2 (4k2+3)(4+3k2)
72t2 72 72
令t=k2+1(t>1),则S= = =
(4t-1)(1+3t) 1 1 1 1
- + +12 - -
t2 t t 2
,
2 49
+
4
1 1 1
又0< <1,故12<- -
t t 2
2 49 49
+ ≤ ,
4 4
288
故 ≤S<6;
49
又当直线l 的斜率不存在时,直线l 的斜率为0,
1 2
1
易得|AB|=4,|CD|=3,此时S= ×4×3=6,
2
288
故S∈ ,6
49
,D正确;
故选:BCD.21 已知抛物线C:y2=2px(p>0)的焦点F与圆E:x2+y2-2x=0的圆心重合,直线l与C交
于A(x ,y )、B(x ,y )两点,且满足OA⋅OB=0(其中O为坐标原点且A,B均不与O重合),则
1 1 2 2
( )
A. xx =16,yy =-16 B. 直线l恒过定点(4,0)
1 2 1 2
C. A,B中点轨迹方程:y2=2x-4 D. △AOB面积的最小值为16
解析:圆E:x2+y2-2x=0可化为(x-1)2+y2=1,
所以E(1,0),半径r=1.
所以抛物线C的焦点为E(1,0),
所以p=2,所以抛物线C的方程为y2=4x.
由题意可知直线l的方程为x=ty+n,
联立直线l与抛物线C的方程可得:
y2-4ty-4n=0,
所以Δ=16t2+16n>0,即t2+n>0,
所以y +y =4t,yy =-4n,
1 2 1 2
y2y2
所以OA⋅OB=xx +yy = 1 2 +yy =n2-4n=0,
1 2 1 2 16 1 2
解得n=4或n=0(舍,否则直线l过原点),
y2y2
所以yy =-16,xx = 1 2 =16,故A正确;
1 2 1 2 16
直线l的方程为x=ty+4,恒过定点(4,0),故B正确;
设AB的中点为M(x,y),
y +y
则y= 1 2 =2t,x=ty+4=2t2+4,
2
消去参数t得:y2=2x-8,故C错误;
因为|AB|= 1+t2|y -y |= 1+t2 (y +y )2-4yy = (1+t2)(16t2+64)=4 (1+t2)(t2+4),
1 2 1 2 1 2
|0-0-4| 4
原点O到直线AB的距离为d= = ,
1+t2 1+t2
1
所以S = ×|AB|×d=8 t2+4,
△OAB 2
所以当t=0时,S =16为最小值,故D正确.
△OAB
故选:ABD.
圆锥曲线黄金55题 23x2 y2
22 已知双曲线Γ: - =1(a>0,b>0),左焦点为F,左右顶点分别为A 、A ,B(0,b),P
a2 b2 1 2
是Γ右支上一动点,且|PF|+|PB|的最小值为( 3+2)a,P关于x轴的对称点为Q,则下列结论
正确的是 ( )
A. Γ的离心率为2 B. PA ⊥AQ
2 1
C. sin∠QPA =sin∠QA A D. 4|PB|≥ 6|PQ|
1 2 1
解析:由题意,F(-c,0),B(0,b),设右焦点为F(c,0),
1
由双曲线定义知,|PF|-|PF|=2a,则|PF|=2a+|PF|,
1 1
∵|BP|+|PF|≥|AF|,∴|BP|+|PF|=|BP|+|PF|+2a≥|BF|+2a= b2+c2+2a,
1 1 1 1
∴ b2+c2+2a=( 3+2)a,
即b2+c2=3a2,∴c2-a2+c2=3a2,
c
∴c2=2a2,即e= = 2(e>1),故A不正确.
a
设P(x,y),Q(-x,-y),A(-a,0),A (a,0),
1 2
y -y -y y y2
∴k = ,k = ,∴k •k = × =- ,
PA2 x-a A1Q x+a A1Q PA2 x+a x-a x2-a2
由A可得双曲线方程为x2-y2=a2,∴k •k =-1,∴PA ⊥AQ,故B正确;
A1Q PA2 2 1
|AN| a+x a+x a+x
记PQ交x轴于点N,sin∠QPA = 1 = = = ,
1 |PA| (a+x)2+y2 2x2+2ax 2x
1
|y| (x-a)(x+a) a+x
sin∠QA A =sin∠QA N= = = ,
2 1 2 (x-a)2+y2 2x(x-a) 2x
∴sin∠QPA =sin∠QA A,故C正确;
1 2 1
假设4|PB|≥ 6|PQ|成立,则4 x2+(y-b)2≥ 6×2|y|,
两边平方得,16[x2+(y-b)2]≥24y2,
∴2x2+2y2-4by+2b2≥3y2,∴y2-4by+2a2+2b2≥0,
∴(y-2b)2≥0,当y=2b时取等号,故D正确;
故选:BCD.
24 公众号:邦达数学x2 y2
23 已知椭圆C: + =1的左右焦点为F,F,若P为椭圆C上一动点,记△PFF 的内心
4 3 1 2 1 2
为I,外心为M,重心为G,且△PFF 内切圆I的半径为r,△PFF 外接圆M的半径为R,则
1 2 1 2
( )
π
A. ∠FPF 的最大值为 B. r的最大值为 3
1 2 3
R
C. PI⋅PG为定值 D. 的最小值为2
r
解析:对于A:在椭圆C中,a=2,b= 3,则c= a2-b2=1,
即点F(-1,0)、F(1,0),由椭圆的定义可得|PF|+|PF|=2a=4,|FF|=2c=2,
1 2 1 2 1 2
(|PF|+|PF|)2
由基本不等式可得|PF|•|PF|≤ 1 2 =4,当且仅当|PF|=|PF|=2时,等号成立,
1 2 4 1 2
|PF|2+|PF|2-|FF|2 (|PF|+|PF|)2-2|PF|⋅|PF|-22 6
所以cos∠FPF = 1 2 1 2 = 1 2 1 2 = -1
1 2 2|PF|⋅|PF| 2|PF|⋅|PF| |PF|⋅|PF|
1 2 1 2 1 2
1 π π
≥ ,又0<∠FPF <π,所以0<∠FPF ≤ ,即∠FPF 的最大值为 ,故A正确;
2 1 2 1 2 3 1 2 3
1
对于B:∵S = r(|PF|+|PF|+|FF|)=(a+c)•r=3r,当点A为椭圆C的短轴的顶点时,
△PF1F2 2 1 2 1 2
S 取最大值
1
×2c×b=bc= 3,∴r=
S △PF1F2
≤
3
,即r的最大值为
3
,故B错误;
△PF1F2 2 3 3 3
对于C:如图,设△PFF 的内切圆与三边分别相切与A,B,C,如图,
1 2
设△PFF 的内切圆与三边分别相切与A,B,C,又G,I分别为△PFF 的重心和内心.
1 2 1 2
|PF|+|PF|-|FF|
则|PB|=|PC|,|FA|=|FC|,|FA|=|FB|,所以|PB|=PC = 1 2 1 2 =a-c,
1 1 2 2 1 2
2 1 1 1 1
所以 PI ⋅ PG = PO•PI = (PF + PF )•PI = PF•PI + PF •PI = |PF|•|PC|
3 3 1 2 3 1 3 2 3 1
1 1 1 4
+ |PF|•|PB|= (PF +PF)•|PB|= (a-c)×2a= ,即PI⋅PG为定值,故C正确;
3 2 3 1 2 3 3
1 1
对于D:S =3r= (|PF|•|PF|sin∠FPF),所以r= (|PF|•|PF|sin∠FPF),
△PF1F2 2 1 2 1 2 6 1 2 1 2
|FF| 1
又 1 2 =2R,所以R= ,
sin∠FPF sin∠FPF
1 2 1 2
1
R sin∠FPF 6
则 = 1 2 =
r 1 |PF|⋅|PF|sin∠FPF
|PF|⋅|PF|sin∠FPF 1 2 1 2
6 1 2 1 2
6
=
6 |PF|⋅|PF| 1- -1
1 2 |PF|⋅|PF| 1 2
圆锥曲线黄金55题 25
2
1 R
= ≥2,所以 的最小值为2,故D正确.
6 r 2-
|PF|⋅|PF| 1 2
故选:ACD.x2 y2 15 1
24 已知F,F 是双曲线C: - =1(a>0,b>0)的左、右焦点,A ,
1 2 a2 b2 2 2
26 公众号:邦达数学
是C上一
2 3
点,若C的离心率为 ,连结AF 交C于点B,则 ( )
3 2
x2
A. C的方程为 -y2=1 B. ∠FAF =90°
3 1 2
C. △FAF 的周长为2 5+2 D. △ABF 的内切圆半径为 5- 3
1 2 1
15 1
解析 A ,
2 2
2 3
是C上一点,C的离心率为 ,
3
15 1
4 4
- =1 a= 3
a2 b2
则 ,解得 b=1 ,
c 2 3
=
a 3 c=2
c2=a2+b2
x2
∴双曲线 -y2=1,故A正确;
3
15 1
∵F(-2,0),F(2,0),A ,
1 2 2 2
,
15 1
∴FA= +2,
1 2 2
15 1
,FA= -2,
2 2 2
15 1
,FA⋅FA= -4+ =0,
1 2 4 4
∴FA⊥FA,故B正确;
1 2
15
| AF | = +2
1 2
2 1
+ -0
2
2
= 8+2 15 = ( 5+ 3)2 = 5 + 3 ,| AF | =
2
15
-2
2
2 1
+ -0
2
2
= 8-2 15 = 5- 3,|FF|=2c=4,周长=2 5+4,故C错误;
1 2
令|BF|=m,
2
则|BF|=2 3+m,|AB|=|AF|+|BF|= 5- 3+m,
1 2 2
在Rt△ABF 中,|BF|2=|AF|2+|AB|2,
1 1 1
3 3+ 5
∴m= ,
11
设△ABF 的周长为l,内切圆半径为r,
1
则l=|AF|+|AB|+|BF|,
1 1
1 1
S = |AF|⋅|AB|= lr,
△ABF1 2 1 2
2S ( 5+ 3)( 5- 3+m)
∴r= △ABF1 = = 5- 3,故D正确;
|AF|+|AB|+|BF| 5+ 3+ 5- 3+m+2 3+m
1 1
故选:ABD.25 抛物线C:y2=6x,AB是C的焦点弦 ( )
A. 点P在C的准线上,则PA⋅PB的最小值为0
B. 以AB为直径的所有圆中,圆面积的最小值为9π
C. 若AB的斜率k= 3,则△ABO的面积S=12
9
D. 存在一个半径为 的定圆与以AB为直径的圆都内切
4
3
解析:抛物线C:y2=6x的焦点F ,0
2
圆锥曲线黄金55题 27
3
,准线x=- ,
2
根据抛物线的性质可知:以AB为直径的圆与准线相切,
若点P不是以AB为直径的圆与准线的切点,则∠PAB为锐角,所以PA⋅PB>0;
若点P是以AB为直径的圆与准线的切点,则PA⊥PB,所以PA⋅PB=0;
综上所述:PA⋅PB的最小值为0,故A正确;
3
设直线AB:x=my+ ,A(x,y),B(x ,y ),
2 1 1 2 2
3
x=my+
联立方程 2 ,消去y得y2-6my-9=0,
y2=6x
则Δ=36m2+36>0,y +y =6m,yy =-9,
1 2 1 2
3
可得|AB|=x +x +3=my +
1 2 1 2
3
+my +
2 2
+3=m(y +y )+6=6(m2+1),
1 2
当m=0时,|AB|取到最小值6,
6
此时以AB为直径的圆的面积最小,最小值为π×
2
2
=9π,故B正确;
3
由选项B可知:以AB为直径的圆的圆心为M3m2+ ,3m
2
,半径R=3m2+3,
9
设圆N的圆心为N(x ,y ),半径r= ,
0 0 4
3
若圆M与圆N内切,则|MN|=R-r,即 x -3m2-
0 2
2 3
+(y -3m)2=3m2+ ,
0 4
27
整理得6x -
0 2
9 3
m2+6y m+ -x -
0 16 0 2
2
-y2=0,
0
27
6x - =0 0 2
因为对任意的m恒成立,则 6y =0
0
9 3 -x -
16 0 2
9
x =
,解得 0 4 ,
y =0 2 -y2=0 0
09
即圆心为N ,0
4
28 公众号:邦达数学
9
,半径r= 的圆恒与以AB为直径的圆都内切,故D正确.
4
3
若AB的斜率k= 3,则m= ,
3
3 3 3 3
直线AB:x= y+ ,即x- y- =0,
3 2 3 2
3 由选项B可得:|AB|=6
3
2 +1
=8,
3
2
点O(0,0)到直线直线AB的距离d=
3
1+-
3
3 3
= ,
2 4
1 3 3
所以△ABO的面积S= ×8× =3 3,故C错误.
2 4
故选:ABD.填空题(共10小题)
x2 y2
26 已知椭圆C: + =1(a>b>0),O(0,0),P(3,1)斜率为-1的直线与C相交于A,B
a2 b2
两点,若直线OP平分线段AB,则C的离心率等于 .
解析:设A,B两点的坐标分别为A(x,y),B(x ,y ),A,B两点中点为M(x ,y ),
1 1 2 2 0 0
x +x y +y
∴x = 1 2 ,y = 1 2 ,
0 2 0 2
1
∵P(3,1),∴直线OP方程为y= x,
3
1
∵M(x ,y )在直线OP上,∴y = x ,
0 0 0 3 0
x2 y2 x2 y2
将A,B两点代入椭圆方程得, 1 + 1 =1, 2 + 2 =1,
a2 b2 a2 b2
x2-x2 y2-y2 (x -x )(x +x ) (y -y )(y +y )
相减得 1 2 + 1 2 =0,∴ 1 2 1 2 =- 1 2 1 2 ,
a2 b2 a2 b2
3
∴化解为3b2=a2,由a2=b2+c2得,a2= c2,
2
c 6
∴e= = .
a 3
6
故答案为: .
3
圆锥曲线黄金55题 29x2 y2
27 设F,F 是椭圆E: + =1(a>b>0)的左、右焦点,过点F 且斜率为 3的直线交椭
1 2 a2 b2 1
圆于点P,若∠PFF =2∠PFF,则椭圆E的离心率为 .
1 2 2 1
解析:因过点F 斜率为 3的直线交椭圆于点P,则有∠PFF =60°,
1 1 2
因为∠PFF =2∠PFF,则∠PFF =30°,
1 2 2 1 2 1
在△PFF 中,可得∠FPF =90°,令椭圆半焦距为c,
1 2 1 2
在Rt△PFF 中可得:|PF|=|FF|cos60°=c,|PF|=|FF|sin60°= 3c,
1 2 1 1 2 2 1 2
由椭圆定义得:2a=|PF|+|PF|=( 3+1)c,
1 2
c 2
可得e= = = 3-1,
a 3+1
所以椭圆E的离心率是e= 3-1.
故答案为: 3-1.
30 公众号:邦达数学28 已知动抛物线y=x2+ax+b(其中a∈R,b≤0)与动直线y=t(t≥1)交于A、B两点且与
动直线y=t+1交于C、D两点,ABCD构成一个梯形,S为这个梯形的面积,AD为其一腰长,
1
则 S2+16AD2的最小值为 .
4
解析:可设A(x,y),B(x ,y ),C(x ,y ),D(x ,y ),且x 0恒成立,
1 1
x +x =-a,xx =b-t,则|AB|=|x -x |= (x +x )2-4xx = a2-4(b-t),
1 2 1 2 1 2 1 2 1 2
由y=t=1与y=x2+ax+b联立,可得x2+ax+b-t-1=0,
则△ =a2-4(b-t-1),由于b≤0,t≥1,可得△ >0恒成立,
2 2
即有x +x =-a,x x =b-t-1,则|CD|=|x -x |= (x +x )2-4x x = a2-4(b-t-1),
3 4 3 4 3 4 3 4 3 4
1 1
可得S= (|AB|+|CD|)×1= ( a2-4(b-t)+ a2-4(b-t-1)),
2 2
-a- a2-4(b-t) -a- a2-4(b-t-1)
又 AD2 = 1 + (x - x )2 = 1 + -
1 4 2 2
圆锥曲线黄金55题 31
2 1
= 1 + (
4
( a2-4(b-t)- a2-4(b-t-1))2,
4
设u= a2-4(b-t),v= a2-4(b-t-1),则v2-u2=4,即v-u= ,
u+v
1 1 1 64
则 S2 + 16AD2 = (u + v)2 + 16 + 4(u - v)2 = (u + v)2 + + 16 ≥
4 16 16 (u+v)2
(u+v)2
64
2 ⋅ +16=4+16=20.
16 (u+v)2
1 64
当且仅当 (u+v)2= 即u+v=4 2时,上式取得等号.
16 (u+v)2
1
则 S2+16AD2的最小值为20.
4
故答案为:20.x2 y2
29 椭圆E: + =1,其左焦点是F,过F的直线与椭圆交于A,B两点(不同于长轴的端
4 3
点),已知点P(-4,0),则:
①直线PA与直线PB的斜率的和为0;
|PA|
②△PAF与△PBF的面积之比为 ;
|PB|
1
③点A到直线x=-4的距离等于 |AF|;
2
9
④S ≤ .
△ABP 2
以上说法中正确的是 .(写出所有正确命题的序号)
解析:由题意知,F(-1,0),设直线AB的方程为x=my-1,A(x,y),B(x ,y ),
1 1 2 2
x=my-1
联立 x2 y2 ,得(3m2+4)y2-6my-9=0,
+ =1
4 3
6m -9
∴y +y = ,y•y = ,
1 2 3m2+4 1 2 3m2+4
y y y(x +4)+y (x +4) y(my +3)+y (my +3)
①k +k = 1 + 2 = 1 2 2 1 = 1 2 2 1
PA PB x +4 x +4 (x +4)(x +4) (x +4)(x +4)
1 2 1 2 1 2
-9 6m
2m⋅ +3⋅
2myy +3(y +y ) 3m2+4 3m2+4
= 1 2 1 2 = =0,即①正确;
(x +4)(x +4) (x +4)(x +4)
1 2 1 2
②∵k +k =0,
PA PB
∴直线PA和直线PB的倾斜角互补,即∠BPF=∠APF,
1 1
∴S = |PA|•|PF|•sin∠APF,S = |PB|•|PF|•sin∠BPF,
△PAF 2 △PBF 2
S |PA|
∴ △PAF = ,即②正确;
S |PB|
△PBF
a2
③椭圆的左准线方程为x=- =-4,
c
设点A到直线x=-4的距离为d,
|AF| c 1
由椭圆的第二定义知, =e= = ,∴d=2|AF|,即③错误;
d a 2
1 1 3 6m
④S = |PF|•|y -y |= •3• (y +y )2-4yy = •
△ABP 2 1 2 2 1 2 1 2 2 3m2+4
32 公众号:邦达数学
2 -9
-4⋅
3m2+4
3 m2+1 m2+1 1 1
= •12• =18• =18• ≤18•
2 (3m2+4)2 [3(m2+1)+1]2
9(m2+1)+6+
1 9+6+1
m2+1
9
= ,当且仅当m=0时,等号成立,即④正确,
2
故答案为:①②④.30 已知P为抛物线y2=4x上任意一点,则点P到y轴的距离与点P到直线l:12x-5y+13=
0的距离之和的最小值为 .
解析:抛物线y2=4x的焦点为F(1,0),准线为l',x=-1,
抛物线y2=4x上的点P到y轴的距离等于它到准线l'的距离d减去1的差,
由抛物线的定义可知,d=|PF|,令点P到直线l:12x-5y+13=0的距离为d',
则点P到y轴的距离与点P到直线l:12-5y+13=0的距离之和为d-1+d'=|PF|+d'-1,
过P作PM⊥l于M,连接PF,MF,过点F作FQ⊥l于点Q,交抛物线y2=4x于点P',如图所
示,
显然|PM|=d',
当点P与点P'不重合时,
有|PF|+d'-1=|PF|+|PM|-1>|MF|-1>|FQ|-1=|P'F|+|P'Q|-1,
则点P是过焦点F作直线l的垂线与抛物线交点时,点P到y轴的距离与点P到直线l:12x-5y
|12×1-5×0+13| 12
+13=0的距离之和取得最小值,最小值为|FQ|-1= -1= .
122+(-5)2 13
12
故答案为: .
13
圆锥曲线黄金55题 3331 某同学在篮球场打球时,无意间发现当球放在地面上时,球的斜上方的一颗灯泡照过来的光
线使得球在地面上留下了影子,这个影子有点像数学课堂上学过的椭圆,但自己还是不太确定这
个想法,于是他回到家里重新翻阅了教材对椭圆这一节知识进行学习和思考,当他读到教材中的
阅读材料后瞬间明白自己的猜想是没有问题的,而且通过学习,他还确定地面和球的接触点(切
点)就是椭圆影子的焦点,如图,地平面上有一个球,其中球的半径为1个单位长度,在球的右上
方有一个灯泡(当成质点),灯泡与地面的距离为3个单位长度,灯泡垂直照射在平面的点为A,
椭圆的顶点中到A点的距离最短时为1个单位长度,则这个椭圆的离心率 .
解析:以A为坐标原点建立平面直角坐标系,由题意可知,|NQ|=a+c,|QR|=a-c,
由题意可得P(0,3),R(-1,0),则PR:3x-y+3=0,k =3,
PR
|3n-1+3| - 10-2
设M(n,1),Q(n,0),则M到PR的距离d= =1,解得n= .
10 3
- 10-2 10-1
则|QR|= -1= =a-c,
3 3
|nk-1+3|
又设PN、PR:kx-y+3=0,由d= =1,得(n2-1)k2+4nk+3=0.
k2+1
3 1 -3
∴k ⋅k = ,则k = ,得x = =3-3n2,
PR PN n2-1 PN n2-1 N k
PN
∴a+c=|NQ|=3n2+n-3= 10+1,
a+c= 10+1
2 10+1 10+2
联立 a-c= 10-1 ,解得a= 3 ,c= 3 .
3
c 6+ 10
∴椭圆的离心率e= = .
a 13
6+ 10
故答案为: .
13
34 公众号:邦达数学x2
32 已知椭圆 +y2=1的左右焦点分别为F,F,过F 的直线AB与椭圆交于AB两点,则
2 1 2 2
△FAB的周长是 ,△FAB内切圆面积的最大值是 .
1 1
x2
解析:由椭圆 +y2=1,得a= 2,b=1,则c= 2-1=1.
2
利用椭圆定义可得△FAB的周长是4a=4 2;
1
1
在△FAB中,设△FAB内切圆的半径为r,则△FAB的面积S= ×4 2r=2 2r,
1 1 1 2
设AB:x=my+1,A(x,y),B(x ,y ),
1 1 2 2
联立直线方程与椭圆方程,可得(m2+2)y2+2my-1=0,
2m 1
∴y +y =- ,yy =- .
1 2 m2+2 1 2 m2+2
1 2m
于是S= |FF|⋅|y -y |=
2 1 2 1 2 m2+2
圆锥曲线黄金55题 35
2 4 2 2 m2+1 2 2
+ = = ≤ 2.
m2+2 m2+2 1
m2+1+
m2+1
当且仅当m=0时上式等号成立.
1
∴2 2r≤ 2,即r≤ .
2
π
∴△FAB内切圆面积的最大值是πr2= .
1 4
π
故答案为:4 2; .
433 已知抛物线C:x2=4y的焦点为F,直线l:x=5,点A,B分别是抛物线C、直线l上的动点,
若点B在某个位置时,仅存在唯一的点A使得|AF|=|AB|,则满足条件的所有|AB|的值为
.
解析:设A(x,y),易知抛物线C:x2=4y焦点为F(0,1),B为直线l:x=5上的动点,
设B(5,a),
∴|AF|= x2+(y-1)2,|PQ|= (x-5)2+(y-a)2,
∵|AF|=|AB|,∴(y-1)2+x2=(y-a)2+(x-5)2,
∴y2-2y+1+x2=y2-2ay+a2+x2-10x+25,
x2
∴-2y+1=-2ay+a2-10x+25,a2-2ay+2y-10x+24=0,x2=4y,即y= 代入,
4
x2 x2
可得a2-2a× +2× -10y+24=0,
4 4
a 1
∴a2- x2+ x2-10x+24=0⇒2a2-ax2+x2-20x+48=0,
2 2
∴(1-a)x2-20x+2a2+48=0,
5
①当a=1时,可得-20x+50=0,解得x= ,
2
x2 1 25 25
由x2=4y,得y= = × = ,
4 4 4 16
此时方程只有一个解,满足题意,
25
∴|AB|= (x-5)2+(y-a)2= -1
16
36 公众号:邦达数学
2 5
+ -5
2
2 41
= ,
16
②当a≠1时,Δ=0,Δ=(-20)2-4(1-a)(2a2+48)=400-4(1-a)(2a2+48)=0,
解得a=-1,代入(1-a)x2-20x+2a2+48=0,可得2x2-20x+50=0,
25 25
求得x=5⇒y= ,可得|AB|= (y-a)2+(x-5)2= +1
4 4
2 29
+(5-5)2= ,
4
29 41
综上所述,|AB|的值为 或 .
4 16
29 41
故答案为: 或 .
4 16x2
34 已知过椭圆E: +y2=1的左焦点F的直线l交E于A,B两点,则|AF|+2|BF|的最小值
2
为 .
x2
解析:如图,由椭圆E: +y2=1,得a= 2,b=1,则c=1.
2
所以左焦点F的坐标为(-1,0),
设直线l的方程为x=my-1,A(x,y),B(x ,y ),
1 1 2 2
x=my-1
由 x2 得(m2+2)y2-2my-1=0,
+y2=1
2
Δ=(-2m)2+4(m2+2)=8(m2+1),
2m -1
由根与系数的关系得y +y = ,yy = ,
1 2 m2+2 1 2 m2+2
1 1 1 1 |y|+|y | |y -y |
+ = + = 1 2 = 1 2 =
|AF| |BF| 1+m2|y| 1+m2|y | 1+m2|yy | 1+m2|yy |
1 2 1 2 1 2
2m
(y +y )2-4yy m2+2
1 2 1 2 =
1+m2|yy |
1 2
圆锥曲线黄金55题 37
2 4 8(1+m2)
+
m2+2 m2+2
= 2 2,
1+m2 1+m2
m2+2 m2+2
1 1
所以 2 2(|AF| +2|BF|) = +
|AF| |BF|
2|BF| |AF|
(|AF| +2|BF|) = 3 + + ≥ 3 +
|AF| |BF|
2|BF| |AF|
2 ⋅ =3+2 2,
|AF| |BF|
当且仅当|AF|= 2|BF|时等号成立,
3+2 2 3 2
所以|AF|+2|BF|≥ =1+ ,
2 2 4
3 2
所以|AF|+2|BF|的最小值为1+ .
4
3 2
故答案为:1+ .
4n
35 已知一族双曲线E :x2-y2= (n∈N*,且n≤2020),设直线x=2与E 在第一象限内
n 2020 n
的交点为A ,点A 在E ,的两条渐近线上的射影分别为B ,∁ ,记△A B ∁ 的面积为a ,则a +
n n n n n n n n n 1
a +a +⋯⋯+a = . .
2 3 2020
n
解析:双曲线E :x2-y2= (n∈N*,且n≤2020)的两条渐近线为y=x,y=-x,互相垂直,
n 2020
n
直线x=2与E 在第一象限内的交点为A ,A 2, 4-
n n n 2020
38 公众号:邦达数学
,
n
2- 4-
2020
点A 在E 的两条渐近线上的射影分别为 B ,∁ ,则|A B |= ,|A C |=
n n n n n n 2 n n
n
2+ 4-
2020
,
2
n
1 2020 n
∴a = |A B ||A C |= = ,
n 2 n n n n 4 8080
1+2020
×2020
1 2 2020 2 2021
∴a +a +a +⋯⋯+a = + +⋯⋯+ = = .
1 2 3 2020 8080 8080 8080 8080 8
2021
故答案为: .
8解答题(共20小题)
x2 y2
36 已知双曲线 - =1(a>b>0)左、右焦点为F,F,其中焦距为2 7,双曲线经过点D
a2 b2 1 2
(4,3).
(1)求双曲线的方程;
(2)过右焦点F 作直线交双曲线于M,N两点(M,N均在双曲线的右支上),过原点O作射线OP,
2
其中OP⊥MN,垂足为E,P为射线OP与双曲线右支的交点,求4|MN|-|OP|2的最大值.
16 9
解析:(1)由题意得 - =1,c= 7,a2+b2=7,解得a=2,b= 3,
a2 b2
x2 y2
双曲线的方程为: - =1.
4 3
(2)当直线MN斜率不存在时,|MN|=3,|OP|=2,则4|MN|-|OP|2=8,
当直线MN斜率存在时,假设直线方程为y=k(x- 7),
联立双曲线方程得(3-4k2)x2+8 7k2x-28k2-12=0,
-8 7k2 -28k2-12
则x +x = ,x ⋅x = ,Δ>0,
1 2 3-4k2 1 2 3-4k2
3
∵直线与双曲线交于右支,∴k2> ,
4
12(1+k2)
则|MN|= 1+k2|x -x |= 1+k2⋅ (x +x )2-4xx = ,
1 2 1 2 1 2 4k2-3
1
设射线OP方程为:y=- x,与双曲线的方程联立,
k
12k2 3 12(k2+1)
∴x2= ,k2> ,|OP|2= ,
3k2-4 4 3k2-4
1 1 1
∴ - = ,
|MN| |OP|2 12
1 1
∴4|MN|-|OP|2=12 -
|MN| |OP|2
圆锥曲线黄金55题 39
|OP|2 4|MN|
(4|MN|-|OP|2)=12 5- +
|MN| |OP|2
|OP|2 4|MN|
≤125-2 ⋅
|MN| |OP|2
=12,
当且仅当|OP|2=4|MN|=36时等号成立,最大值为12.
综上,4|MN|-|OP|2的最大值为12.x2 y2 3
37 已知A,B分别是椭圆C: + =1(a>b>0)的左,右顶点,P1,
a2 b2 2
40 公众号:邦达数学
为椭圆C上的
1
点,直线PA,PB的斜率之积为- .
4
(1)求椭圆C的方程;
(2)直线l与椭圆C交于M,N两点,且直线AM与BN相交于点D,若点D在直线x=4上,证明:
直线l过定点.
解析:(1)由题可知A(-a,0),B(a,0),
3 3 3
2 2 4 1
所以k ⋅k = ⋅ = =- ,解得a=2.
PA PB 1-a 1+a 1-a2 4
3
因为P1,
2
为椭圆C上的点,
1 3
所以 + =1,解得b2=1,
4 4b2
x2
所以椭圆C的方程为 +y2=1.
4
(2)证明:设D(4,y ),由(1)有A(-2,0),B(2,0),点D在直线AM上,
0
y y
则k = 0 ,则直线AM的方程为y= 0 (x+2).
AM 4+2 6
x
4
2 +y2=1
联立直线与椭圆方程得 ,消去y整理得(y2+9)x2+4y2x+4y2-36=0,
y 0 0 0
y= 0 (x+2)
6
-2y2+18
解得x=-2或x= 0 .
y2+9
0
-2y2+18 y 6y
将x= 0 代入y= 0 (x+2),可得y= 0 ,
y2+9 6 y2+9
0 0
-2y2+18 6y
所以点M的坐标为 0 , 0
y2+9 y2+9
0 0
.
2y2-2 -2y
同理可得点N的坐标为 0 , 0
y2+1 y2+1
0 0
.
当y2=3时,直线l的方程为x=1,直线l过定点(1,0).
0
6y -2y
0 - 0
-2y y2+9 y2+1 2y2-2
当y2≠3时,所以直线l的方程为y- 0 = 0 0 x- 0
0 y2+1 -2y2+18 2y2-2 y2+1
0 0 - 0 0
y2+9 y2+1
0 0
,
2y 8y (y2+3) 2y2-2
整理可得y+ 0 = 0 0 x- 0
y2+1 4(9-y4) y2+1
0 0 0
2y 2y2-2
= 0 x- 0
3-y2 y2+1
0 0
.
2y 3-y2 2y2-2 3-y2+2y2-2 y2+1
令y=0,则x= 0 ⋅ 0 + 0 = 0 0 = 0 =1,
y2+1 2y y2+1 y2+1 y2+1
0 0 0 0 0
所以直线l过定点(1,0).
综上,直线l过定点(1,0).x2 y2 3
38 已知椭圆 + =1(a>b>0)的焦距为2 3,离心率为 ,椭圆的左右焦点分别为F、
a2 b2 2 1
F,直角坐标原点记为O.设点P(0,t),过点P作倾斜角为锐角的直线l与椭圆交于不同的两点
2
B、C.
(1)求椭圆的方程;
(2)设椭圆上有一动点T,求PT⋅(TF -TF)的取值范围;
1 2
(3)设线段BC的中点为M,当t≥ 2时,判别椭圆上是否存在点Q,使得非零向量OM 与向量
PQ平行,请说明理由.
x2 y2 3
解析:(1)∵椭圆 + =1(a>b>0)的焦距为2 3,离心率为 ,
a2 b2 2
c 3 x2
∴c= 3,e= = ,可得a=2,∴b= a2-c2=1,∴椭圆的标准方程为 +y2=1;
a 2 4
(2)设动点T(x,y),FF =(2 3,0),PT=(x,y-t),PT⋅(TF -TF)=-PT⋅FF =-2 3x,
1 2 1 2 1 2
∵x∈[-2,2],∴PT⋅(TF -TF)的取值范围为[-4 3,4 3];
1 2
(3)显然直线的斜率存在,故可设直线l:y=kx+t,
y=kx+t
联立 x2 ,消去y得(1+4k2)x2+8ktx+4t2-4=0,
+y2=1
4
t2-1
Δ=-16t2+64k2+16>0,即k2> ①,设B(x,y)、C(x ,y ),
4 1 1 2 2
8kt 4t2-4
由根与系数的关系可得x +x =- ,xx = ,
1 2 1+4k2 1 2 1+4k2
x +x 4kt y +y k(x +x )+2t 4k2t t
则 1 2 =- , 1 2 = 1 2 =- +t= ,
2 1+4k2 2 2 1+4k2 1+4k2
4kt t
则x =- ,
M 1+4k2 1+4k2
圆锥曲线黄金55题 41
1
,故k =- ,
OM 4k
1 1
若OM ∥PQ,则有k =k =- ,设直线PQ为y=- x+t,
PQ OM 4k 4k
1
y=-
4k
x+t
1
联立 ,消去y有1+
x2 4k2
+y2=1
4
2t
x2- x+4t2-4=0,
k
4t2 1
要使得存在点Q,则Δ = -41+
2 k2 4k2
(4t2-4)≥0,
4 1 t2-1 1
整理得16+ -16t2≥0,故k2≤ ②,由①②式得, b>0)的焦距为2 6,且过点A(2,1).
a2 b2
(Ⅰ)求椭圆C的方程;
(Ⅱ)若不经过点A的直线l:y=kx+m与C交于P,Q两点,且直线AP与直线AQ的斜率之和
为0,证明:直线PQ的斜率为定值.
解析:(Ⅰ) 因为椭圆C的焦距为2 6,且过点A(2,1),
4 1
所以 + =1,2c=2 6.⋯(2分)
a2 b2
因为a2=b2+c2,解得a2=8,b2=2,⋯(3分)
x2 y2
所以椭圆C的方程为 + =1.⋯(4分)
8 2
证明:(Ⅱ)设点P(x,y),Q(x ,y ),则y =kx +m,y =kx +m,
1 1 2 2 1 1 2 2
y=kx+m
由 x2 y2 ,消去y得(4k2+1)x2+8kmx+4m2-8=0,(*).⋯(5分)
+ =1
8 2
8km 4m2-8
则x +x =- ,xx = ,⋯(6分)
1 2 4k2+1 1 2 4k2+1
y -1 y -1
因为k +k =0,即 1 =- 2 ,⋯(7分)
PA QA x -2 x -1
1 2
化简得xy +x y -(x +x )-2(y +y )+4=0.
1 2 2 1 1 2 1 2
即2kxx +(m-1-2k)(x +x )-4m+4=0.(**) ⋯(8分)
1 2 1 2
2k(4m2-8) 8km(m-1-2k)
代入得 - -4m+4=0,⋯(9分)
4k2+1 4k2+1
整理得(2k-1)(m+2k-1)=0,
1
所以k= 或m=1-2k.⋯(10分)
2
若m=1-2k,可得方程(*)的一个根为2,不合题意.⋯(11分)
1
所以直线PQ的斜率为定值,该值为 .⋯(12分)
2
42x2 y2
40 已知双曲线Γ: - =1,A(2,2)是双曲线Γ上一点.
3 12
(1)若椭圆C以双曲线Γ的顶点为焦点,长轴长为4 3,求椭圆C的标准方程;
(2)设P是第一象限中双曲线Γ渐近线上一点,Q是双曲线Γ上一点,且PA=AQ,求△POQ的面
积S(O为坐标原点);
(3)当直线l:y=-4x+m(常数m∈R)与双曲线Γ的左支交于M、N两点时,分别记直线AM、
AN的斜率为k、k ,求证:k +k 为定值.
1 2 1 2
x2 y2
解析:(1)因为双曲线的方程为 - =1,所以双曲线的左右顶点为(± 3,0),
3 12
x2 y2
设椭圆方程为 + =1(a>b>0),所以2a=4 3,c= 3,
a2 b2
a2=12 x2 y2
所以 ,所以椭圆C的标准方程为 + =1
b2=a2-c2=9 12 9
(2)因为双曲线的渐近线方程为y=±2x,
不妨设P(t,2t)(t>0),
x -2=2-t
Q
又PA=AQ,所以 ,
y -2=2-2t
Q
所以Q(4-t,4-2t),又因为Q是双曲线上一点,
(4-t)2 (4-2t)2
9
所以 - =1,解得t= ,
3 12 4
9 9
所以P ,
4 2
圆锥曲线黄金55题 43
7 1
,Q ,-
4 2
,
9
所以|OP|= -0
4
2 9
+ -0
2
2 9 5
= ,
4
7 1
2× --
4 2
又Q到直线OP:2x-y=0的距离d=
4 5
= ,
1+4 5
1 1 4 5 9 5 9
所以S= ×d×|OP|= × × = ;
2 2 5 4 2
(3)设M(x,y),N(x ,y ),
1 1 2 2
y=-4x+m
联立直线与双曲线方程得 x2 y2 ,消去y得12x2-8mx+m2+12=0,
- =1
3 12
Δ=64m2-48(m2+12)>0,即m2-36>0,
8m 2m m2+12
所以x +x = = ,xx = ,
1 2 12 3 1 2 12
2m
又因为M,N为左支上两点,所以x +x = <0,所以m<-6,
1 2 3
y -2 y -2 -4x +m-2 -4x +m-2
所k +k = 1 + 2 = 1 + 2
1 2 x -2 x -2 x -2 x -2
1 2 1 2
-4x +8+m-10 -4x +8+m-10
= 1 + 2 ,
x -2 x -2
1 2
m-10 m-10 x +x -4
所以k +k =-8+ + =-8+(m-10)× 1 2 ,
1 2 x -2 x -2 xx -2(x +x )+4
1 2 1 2 1 2
2m 2
-4 (m-6)
3 3
所以k +k =-8+(m-10)× =-8+(m-10)× ,
1 2 m2+12 2m (m-6)(m-10)
-2× +4
12 3 12
所以k +k =-8+8=0,所以k +k 为定值0.
1 2 1 24 12
41 已知中心在原点,焦点在x轴上的椭圆C,其离心率e= ,点P3,
5 5
在椭圆上.
(1)求椭圆的标准方程;
(2)过椭圆的左顶点A作两条直线,分别与椭圆C交于M、N两点,满足AM⊥AN,求点Q(4,0)
到直线MN距离d的最大值.
x2 y2
解析:(1)由题意设椭圆的标准方程为 + =1(a>b>0),
a2 b2
c 4 9 144
则 = ,a2=b2+c2, + =1,
a 5 a2 25b2
联立解得a2=25,b2=9,
x2 y2
∴椭圆的标准方程为 + =1.
25 9
(2)A(-5,0),设M(x,y),N(x ,y ),
1 1 2 2
不妨设直线MN的方程为my=x-t,-50,化为t2<25(m2+1).
18mt 9t2-225
∴y +y =- ,yy = .
1 2 9m2+25 1 2 9m2+25
∵AM⊥AN,
∴AM•AN =(x +5,y)•(x +5,y )=0,
1 1 2 2
化为(my +t+5)•(my +t+5)+yy =0,
1 2 1 2
化为(mt+5m)(y +y )+(m2+1)yy +(t+5)2=0,
1 2 1 2
18mt
代入可得(mt+5m)-
9m2+25
9t2-225
+ (m2+1)+(t+5)2=0,
9m2+25
化为:17t2+125t+200=0,
40
解得t=-5或t=- ,
17
t=-5舍去,
40
t=- 满足Δ>0.
17
|4-t| 108 108
点Q(4,0)到直线MN距离d= = ≤ ,m=0时取等号.
m2+1 17 m2+1 17
108
即点Q(4,0)到直线MN距离d的最大值为 .
17
4442 已知A(0,2),B(0,-2),P为平面上的一个动点.设直线AP,BP的斜率分别为k ,k ,且
1 2
1
满足k ⋅k =- .记动点P的轨迹为曲线C.
1 2 3
(1)求曲线C的方程;
3 1
(2)过点M ,-
2 2
圆锥曲线黄金55题 45
的动直线l与曲线C交于E,F两点.曲线C上是否存在定点N,使得NE
1 1
⊥NF恒成立(直线l不经过点N)?若存在,求出点N的坐标,并求 + 的最小值;若不存
|NE|2 |NF|2
在,请说明理由.
解析:(1)设点P(x,y),则x≠0,
1 y-2 y+2 1
因为k ⋅k =- ,所以 ⋅ =- ,
1 2 3 x x 3
x2 y2
整理,得 + =1,
12 4
x2 y2
所以曲线C的方程为 + =1(x≠0).
12 4
3
(2)当直线l的斜率不存在时方程为x= ,
2
3 y2 13
代入曲线C的方程中,得 + =1,解得y=± ,
16 4 2
3 13
所以此时E ,
2 2
3 13
,F ,-
2 2
,
x2 y2
设N(x ,y ),则 0 + 0 =1①,
0 0 12 4
3 13
NE= -x , -y
2 0 2 0
3 13
,NF= -x ,- -y
2 0 2 0
,
3
因为NE⊥NF,所以NE⋅NF= -x
2 0
2 13
+y2- =0②,
0 4
3
联立①②,解得x =3或 (舍去),y =±1,所以N(3,1)或(3,-1),
0 2 0
当N(3,1)时,且当直线l的斜率存在时,
设直线l方程为y=kx+b,E(x,y),F(x ,y ),
1 1 2 2
3 1
因为直线l经过 ,-
2 2
3 1
时,所以 k+b=- ,
2 2
y=kx+b
联立 x2 y2 ,得(1+3k2)x2+6kbx+3b2-12=0,
+ =1
12 4
-6kb 3b2-12
所以x +x = ,xx = ,
1 2 1+3k2 1 2 1+3k2
所以NE=(x -3,y -1),NF=(x -3,y -1),
1 1 2 2
所以NE⋅NF=(x -3)(x -3)+(kx +b-1)(kx +b-1)
1 2 1 2
=(1+k2)xx +(kb-k-3)(x +x )+b2-2b+10
1 2 1 2
(1+k2)(3b2-12)+(kb-k-3)(-6kb)+(b2-2b+10)(1+3k2)
=
1+3k2
4b2-2+18k2+18kb-2b
=
1+3k2
1 3
4- - k
2 2
=
2 1 3
-2+18k2+18k- - k
2 2
1 3
-2- - k
2 2
1+3k2
9k2+6k+1-2+18k2-9k-27k2+1+3k
= =0,
1+3k2
所以NE⋅NF=0,即NE⊥NF,
-6k
当N(3,-1)时,同理可得NE⋅NF= ,所以此时NE⊥NF不恒成立,
1+3k2
1
1+
2
所以存在定点N(3,1)使NE⊥NF,k≠ =1,
3
3-
2
设点N到直线l的距离为d,因为三角形NEF为直角三角形,
所以|NE|2+|NF|2=|EF|2,|NE|•|NF|=|EF|•d,
1 1 |NE|2+|NF|2 |EF|2 1
所以 + = = = ,
|NE|2 |NF|2 |NE|2⋅|NF|2 (|EF|⋅d)2 d2
3 1 4
当直线l斜率不存在时,d= , = ,
2 d2 9
1 3
当直线l斜率存在时,设直线l的方程为y+ =kx-
2 2
46
,
3 3
k-
2 2 1 4 1+k2 4 2k
则d= , = ⋅ = 1+
1+k2 d2 9 k2-2k+1 9 k2-2k+1
,
1 4
当k=0时, = ;
d2 9
1 4 2k
当k>0时, = 1+
d2 9 (k-1)2
4
> ;
9
1 4 2
当k<0时, = 1+
d2 9 1 k-2+ k
4 2
= 1+
9 1 --k- k
-2
2
≥ ,
9
当且仅当k=-1时等号成立,
1 1 2
综上,存在定点N(3,1)使NE⊥NF, + 的最小值为 .
|NE|2 |NF|2 9x2 y2
43 已知点(2,3)在双曲线C: - =1上.
a2 a2+2
(1)双曲线上动点Q处的切线交C的两条渐近线于A,B两点,其中O为坐标原点,求证:△AOB
的面积S是定值;
1
(2)已知点P ,1
2
圆锥曲线黄金55题 47
,过点P作动直线l与双曲线右支交于不同的两点M、N,在线段MN上取异于
|PM| |MH|
点M、N的点H,满足 = ,证明:点H恒在一条定直线上.
|PN| |HN|
x2 y2
解析:(1)证明:因为点(2,3)在双曲线C: - =1上,
a2 a2+2
4 9 y2
所以 - =1,解得a2=1,则双曲线方程为x2- =1,
a2 a2+2 3
当切线方程的斜率存在时,不妨设过点(x ,y )的切线方程为y-y =k(x-x ),
0 0 0 0
y-y =k(x-x )
0 0 1 k2
联 立 x2 y2 ,消 去 y 并 整 理 得 -
- =1 a2 b2
a2 b2
2k2x 2k2y
x 2 + 0 - 0
b2 b2
x +
2kx y -k2x2-y2-b2 2k2x 2k2y
0 0 0 0 =0,因为Δ= 0 - 0
b2 b2 b2
2 1 k2
-4 -
a2 b2
2kx y -k2x2-y2-b2
⋅ 0 0 0 0 =0,
b2
y-y y-y
即(y -kx )2=a2k2-b2,又k= 0 ,可得y - 0 ⋅x
0 0 x-x 0 x-x 0
0 0
2 y-y
=a2 0
x-x
0
2
-b2,
所以(xy -x y)2=a2(y-y )2-b2(x-x )2,
0 0 0 0
(xy -x y)2 (y-y )2 (x-x )2
对等式两边同除以a2b2,得 0 0 = 0 - 0 ,
a2b2 b2 a2
x2y2-2xy x y+x2y2 y2-2y y+y2 x2-2x x+x2
即 0 0 0 0 = 0 0 - 0 0 ,
a2b2 b2 a2
x2 y2 x2 y2
因为 0 - 0 =1, - =1,
a2 b2 a2 b2
x2y2-2xy x y+x2y2 2y y 2x x
所以 0 0 0 0 =-2- 0 + 0 ,
a2b2 b2 a2
x2 0 - y2 0 =1
a2 b2 x2x2 x2y2 x2y2 y2y2
联立 ,两式相乘得 0 - 0 - 0 + 0 =1,
x2 y2 a4 a2b2 a2b2 b4
- =1
a2 b2
x2y2 x2y2 x2x2 y2y2
所以 0 + 0 =-1+ 0 + 0 ,
a2b2 a2b2 a4 b4
x2x2 y2y2 -2xy x y 2y y 2x x
可得-1+ 0 + 0 + 0 0 =-2- 0 + 0 ,
a4 b4 a2b2 b2 a2
x x y y
即-1+ 0 - 0
a2 b2
2 x x y y
=-2+2 0 - 0
a2 b2
,
x x y y
不妨令t= 0 - 0 ,此时-1+t2=-2+2t,
a2 b2
x x y y
即(t-1)2=0,解得t=1,所以 0 - 0 =1,
a2 b2
当切线斜率不存在时,
x x y y
此时切点为(±a,0),切线方程为x=±a,满足 0 - 0 =1,
a2 b2
x2 y2 x x y y
综上, - =1(a>0,b>0)上一点(x ,y )的切线方程为 0 - 0 =1,
a2 b2 0 0 a2 b2不妨设Q(m,n),
y2 ny
此时x2- =1过点Q(m,n)的切线方程为mx- =1,
3 3
ny y2
所以mx- =1为x2- =1过点Q(m,n)的切线方程,
3 3
易知双曲线的两条渐近线方程为y=± 3x,
3
mx- ny =1 x 1 = 3m- 3n
联立 3 ,解得
,
3 3
y= 3x y =
1 3m- 3n
3
mx- ny =1 x 2 = 3m+ 3n
联立 3 ,解得
,
-3 3
y=- 3x y =
2 3m+ 3n
y-y y -y
所以直线AB方程为 1 = 2 1 ,
x-x x -x
1 2 1
即(y-y)(x -x)-(y -y)(x-x)=0,
1 2 1 2 1 1
|(-y)(x -x)-(y -y)(-x)| |xy -x y|
此时点O到直线AB的距离为 1 2 1 2 1 1 = 1 2 2 1 ,
(x -x)2+(y -y) (x -x)2+(y -y)
2 1 2 1 2 1 2 1
又|AB|= (x -x)2+(y -y),
2 1 2 1
1 |xy -x y| 1
则△AOB的面积S= 1 2 2 1 ⋅ (x -x)2+(y -y)= |xy -x y|
2 (x -x)2+(y -y) 2 1 2 1 2 1 2 2 1
2 1 2 1
1 3 -3 3 3 3 3
= ⋅ - ⋅
2 3m- 3n 3m+ 3n 3m+ 3n 3m- 3n
1 -18 3 1 -18 3
= = = 3,为定值;
2 9m2-3n2 2 9
(2)证明:若直线l斜率不存在,此时直线l与双曲线右支无交点,不合题意,不满足条件,
所以直线l斜率存在,
1
不妨设直线l方程y-1=kx-
2
48
,M(x,y),N(x ,y ),
1 1 2 2
1
y-1=kx-
2
联立
1
y2 ,消去y并整理得(3-k2)x2+(k2-2k)x- 4 k2-k+4
x2- =1
3
=0,
Δ>0
3-k2≠0
k2-2k 1 1
易知 >0 ,因为 k2-k+4= (k-2)2+3>0恒成立,
k2-3 4 4
1
k2-k+4
4
>0
k2-3
-2-2 13
所以k2-3>0,即k2-2k>0,解得 0,b>0),
a2 b2
b
不妨设右焦点为(c,0),渐近线方程为y=± x.
a
bc
a
右焦点到渐近线的距离d= =b= 2.
b2
+1
a2
因为C为等轴双曲线,所以a=b= 2.
所以C的方程为x2-y2=2.
(2)证明:设P(x,y),Q(x ,y ),
1 1 2 2
2
由OP⋅OQ=|OP|⋅|OQ|⋅cos45°,得xx +yy = |OP|⋅|OQ|,
1 2 1 2 2
且|OP|2=x2+y2=2x2-2=2y2+2,|OQ|2=x2+y2=2x2-2=2y2+2,
1 1 1 1 2 2 2 2
1
所以y2y2= |OP|2⋅|OQ|2+x2x2- 2xx ⋅|OP|⋅|OQ|,
1 2 2 1 2 1 2
|OP|2-2 |OQ|2-2 1 |OP|2+2 |OQ|2+2
则 ⋅ = |OP|2⋅|OQ|2+ ⋅ - 2xx ⋅|OP|⋅|OQ|,
2 2 2 2 2 1 2
即|OP|2.|OQ|2+2|OP|2+2|OQ|2=2 2xx ⋅|OP|⋅|OQ|,
1 2
|OP|2+2 |OQ|2+2
平方后得(|OP|2⋅|OQ|2+2|OP|2+2|OQ|2)2=8× ⋅ ⋅|OP|2⋅|OQ|2,
2 2
等式两边同时除以|OP|4•|OQ|4,
2 2
得1+ +
|OP|2 |OQ|2
50
2 2
=21+
|OP|2
2
1+
|OQ|2
,
4 4 1 1 1
即 + =1,即 + = .
|OP|4 |OQ|4 |OP|4 |OQ|4 4
1 1 1
所以 + 是定值,且该定值为 .
|OP|4 |OQ|4 46
45 已知离心率e= 的椭圆Γ的中心在原点O,焦点在x轴上,直线l交Γ于A、B两点,且
3
CA=2BC,其中,点C(-1,0).
(1)求△OAB的面积S的最大值,并求此时椭圆Γ的方程;
(2)对于(1)的椭圆Γ上,若存在不同的两点关于直线y=3x+m对称,求m的取值范围.
x2 y2
解析:(1)设椭圆的方程为 + =1(a>b>0),
a2 b2
c 6
由e= = 及a2=b2+c2,得a2=3b2,
a 3
故椭圆的方程为x2+3y2=3b2,①
设A(x,y),B(x ,y ),由CA=2BC,
1 1 2 2
x +1=-2(x +1)
1 2
得(x
1
+1,y
1
)=2(-1-x
2
,-y
2
),即 ,②
y =-2y
1 2
由题意,直线l过点C(-1,0),
当直线l斜率不存在时,显然不满足CA=2BC,
当直线l斜率为0时,O,A,B三点共线,不构成三角形,
故直线l的斜率存在且不为0,设直线l方程为y=k(x+1),
将y=k(x+1)代入椭圆方程,
得(3k2+1)x2+6k2x+3k2-3b2=0,则Δ=k2(3b2-1)+b2>0,
6k2 3k2-3b2
所以x +x =- ,③,xx = ,④,
1 2 3k2+1 1 2 3k2+1
1 3 3
所以S = |y -y |⋅|OC|= |y |= |k|⋅|x +1|,
△OAB 2 1 2 2 2 2 2
2
联立②③,得x +1=- ,
2 3k2+1
3|k|
所以S = (k≠0),
△OAB 3k2+1
3 3 3
故S = ≤ = ,
△OAB 1 2 3 2
3|k|+
|k|
1 3
当且仅当3|k|= ,即k=± 时,S 取得最大值,
|k| 3 △OAB
此时x +x =-1,又因为x +1=-2(x +1),所以x =1,x =-2,
1 2 1 2 1 2
代入④,得3b2=5,故此时椭圆的方程为x2+3y2=5;
(2)设椭圆Γ上存在不同的两点M(x ,y ),N(x ,y )关于直线y=3x+m对称,
3 3 4 4
x2+3y2=5
3 3
则有
x2+3y2=5
,设MN的中点为P(x
0
,y
0
),
4 4
x 1
则两式相减得:x2-x2=-3(y2-y2),整理得: 0 =-3×-
3 4 3 4 y 3
0
圆锥曲线黄金55题 51
,
m
y 0 =x 0 x 0 =- 2
所以
y =3x +m
,即
m
,
0 0 y 0 =- 2
由题意,点P(x ,y )在椭圆内,则有x2+3y2<5,
0 0 0 0
m2 m2
即 +3× <5,化简得m2<5,解得- 50)与椭圆 + =1有公共的焦点.
5 4
(1)求抛物线C的方程;
(2)过Q(-3,-2)的直线l交抛物线C于A,B两点,试问在抛物线C上是否存在定点P,使得直
线PA,PB的斜率存在且非零时,满足两直线的斜率之积为1,若存在.请求出点P的坐标,若不存
在,请说明理由.
x2 y2
解析:(1)椭圆 + =1的焦点为(±1,0),
5 4
由题意知,抛物线C:y2=2px(p>0)的焦点为(1,0),
p
则 =1,p=2,故抛物线C的方程为y2=4x.
2
y2
(2)假设存在定点P,设P 0 ,y
4 0
52
,
设直线l方程为y+2=k(x+3)(k≠0),即y=kx+3k-2,
y=kx+3k-2
联立 ,可得k2x2+(6k2-4k-4)x+(3k-2)2=0,
y2=4x
1
由Δ=-48k2+32k+16>0,解得- b>0)的离心率为 ,过椭圆焦点并且垂直于长轴的弦长度为
a2 b2 2
1.
(1)求椭圆C的标准方程;
(2)若直线l与椭圆C相交于A,B两点,与y轴相交于M(0,m)点,若存在实数m,使得OA+
3OB=4OM,求m的取值范围.
3 c 3 c2 3 a2-b2 3 b2 1
解析:(1)因为该椭圆的离心率为 ,所以有 = ⇒ = ⇒ = ⇒ = ①,
2 a 2 a2 4 a2 4 a2 4
x2 y2 c2
在方程 + =1中,令x=±c,解得y2=b21-
a2 b2 a2
圆锥曲线黄金55题 53
b4 b2
= ⇒y=± ,
a2 a
因为过椭圆焦点并且垂直于长轴的弦长度为1,
b2 b2
所以有 --
a a
a=2 x2
=1②,由(1),(2)可得: ,所以椭圆的方程为 +y2=1.
b=1 4
(2)当直线l不存在斜率时,由题意可知直线与椭圆有两个交点,与纵轴也有两个交点,不符合题
意;当直线l存在斜率时,设为k,所以直线l的方程设为y=kx+m,
x2
+y2=1
于是有 4 ⇒(1+4k2)x2+8kmx+4m2-4=0,
y=kx+m
因为该直线与椭圆有两个交点,所以一定有Δ=64k2m2-4(1+4k2)(4m2-4)>0,
化简,得4k2-m2+1>0,
8km 4m2-4
设A(x,y),B(x ,y ),于是有x +x =- ,xx = ,
1 1 2 2 1 2 1+4k2 1 2 1+4k2
因为OA+3OB=4OM,
所以(x,y)+3(x ,y )=4(0,m)⇒x +3x =0⇒x =-3x ,
1 1 2 2 1 2 1 2
8km 8km 4km
代入x +x =- 中,得-3x +x =- ⇒x = ,
1 2 1+4k2 2 2 1+4k2 2 1+4k2
4m2-4 4km
于是有(-3x )⋅x = ⇒-3
2 2 1+4k2 1+4k2
2 4m2-4
= ,
1+4k2
m2-1 m2-1 1
化简,得k2= ,代入4k2-m2+1>0中,得4⋅ -m2+1>0⇒ 0且3k2-1>0,得 |EF|=2 6,
∴P点轨迹是以E,F为焦点,4 2为长轴长的椭圆,
x2 y2
∴曲线C的方程为 + =1.
8 2
x2 y2
(2)由(1)可知C的方程为 + =1,设点P(x ,y )(x >0,y >0),D(0,m),H(0,n),
8 2 0 0 0 0
y -m
则直线PD的方程为y= 0 x+m,即(y -m)x-x y+mx =0,
x 0 0 0
0
∵圆M:(x+1)2+y2=1的圆心为M(-1,0),半径为1,直线PD与圆相切,
|-y +m+x m|
∴圆心M到直线PD的距离为1,即 0 0 =1,
(y -m)2+x2
0 0
即(y -m)2+x2=(y -m)2-2x m(y -m)+x2m2,
0 0 0 0 0 0
即(x +2)m2-2y m-x =0,同理(x +2)n2-2y n-x =0.
0 0 0 0 0 0
由此可知,m,n为方程(x +2)x2-2y x-x =0的两个实根,
0 0 0
2y x
∴m+n= 0 ,mn=- 0 ,
x +2 x +2
0 0
4y2 4x 4x2+4y2+8x
∴|DH|=|m-n|= (m+n)2-4mn= 0 + 0 = 0 0 0 .
(x +2)2 x +2 (x +2)2
0 0 0
x2 y2 x2
∵点P(x ,y )在椭圆C上,则 0 + 0 =1,则y2=2- 0 ,
0 0 8 2 0 4
3x2+8x +8 3
则|DH|= 0 0 = ,
(x +2)2 2
0
x2
则3x2-4x -4=0,∵x >0,则x =2,y2=2- 0 =1,即y =1,
0 0 0 0 0 4 0
故存在点P(2,1)满足题设条件.
x2 y2
(3)由(1)可知C的方程为 + =1,由题意,直线斜率存在,
8 2
设l:y=kx+m,且A(x,kx +m),B(x ,kx +m),
1 1 2 2
y=kx+m
联立方程组 x2 y2 ,整理得(4k2+1)x2+8kmx+4m2-8=0,
+ =1
8 2
则Δ=(8km)2-4(4k2+1)(4m2-8)>0,可得m2<8k2+2,
8km 4m2-8
且x +x =- ,xx = ,
1 2 4k2+1 1 2 4k2+1
∵直线PA,PB的倾斜角互补,∴k +k =0,
PA PB
kx +m-1 kx +m-1
可得 1 + 2 =0,整理得2kxx +(m-1-2k)(x +x )-4(m-1)=0,
x -2 x -2 1 2 1 2
1 2
圆锥曲线黄金55题 558km 4m2-8 4m2-8 8km
将x +x =- ,x x = 代入上式,可得2k⋅ +(m-1-2k)-
1 2 4k2+1 1 2 4k2+1 4k2+1 4k2+1
56
-4
(m-1)=0,
即4k2+(2m-4)k+1-m=0,即(2k-1)(2k+m-1)=0,
1
解得k= 或2k+m-1=0,
2
当2k+m-1=0时,即m=1-2k,可得y=kx+1-2k,即y-1=k(x-2),
1
此时直线l经过点P(2,1),不符合题意,∴直线l的斜率为 .
250 在平面直角坐标系xOy中,动点M在抛物线y2=36x上运动,点M在x轴上的射影为N,动
1
点P满足PN = MN.
3
(Ⅰ)求动点P的轨迹E的方程;
(Ⅱ)过点D(-3,2)作直线与曲线E顺次交于A、B两点,过点A作斜率为1的直线与曲线E的另
一个交点为点C,求证:直线BC过定点.
解析:(Ⅰ)设点P(x,y),M(x ,y ),
0 0
则y2=36x ,且N(x ,0),
0 0 0
由P N = 1 M N ,得 x=x 1 0 ,∴ x 0 =x ,
3 y= y y =3y
3 0 0
代入y2=36x ,得9y2=36x,∴y2=4x.
0 0
∴动点P的轨迹E的方程为y2=4x.
(Ⅱ)证明:显然,直线AB斜率存在,设AB的方程为y-2=k(x+3),
y-2=k(x+3)
由 ,得ky2-4y+8+12k=0,k≠0,则Δ=16(-3k2-2k+1)>0,
y2=4x
4 8
设A(x,y),B(x ,y ),则y +y = ,yy = +12,
1 1 2 2 1 2 k 1 2 k
∴yy -12=2(y +y )①,
1 2 1 2
y2
直线AC的方程为y-y =x- 1 ,
1 4
y2
y-y =x- 1
由 1 4 ,得y2-4y+4y -y2=0,Δ=16-4(4y -y2)>0,
1 1 1 1
y2=4x
设C(x ,y )则y +y =4②,
3 3 1 3
由①②,得(4-y )y -12=2(4-y +y ),∴2(y +y )=y y +20③.
3 2 3 2 2 3 2 3
(i)若直线BC斜率斜率不存在,则y +y =0,又2(y +y )=y y +20,
2 3 2 3 2 3
y2
∴y2=20,∴x = 3 =5,∴BC的方程为x=5;
3 3 4
y -y 4
(ii)若直线BC斜率存在,则 2 3 = ,
x -x y +y
2 3 2 3
4 y2
直线BC的方程为y-y = x- 2
2 y +y 4
2 3
圆锥曲线黄金55题 57
,即4x-(y +y )y+y y =0,
2 3 2 3
将③代入,得4x-(y +y )y+2(y +y )-20=0,
2 3 2 3
∴(y +y )(2-y)+4(x-5)=0,
2 3
故直线BC斜率存在时过点(5,2).
由(i)(ii)知,直线BC过点(5,2).x2 y2 2 5
51 已知椭圆Γ: + =1(a>b>0)的长轴长为2 5,离心率为 ,斜率为k的直线l与
a2 b2 5
椭圆Γ有两个不同的交点A,B.
(1)求Γ的方程;
(2)若直线l的方程为y=x+t,点M(0,1)关于直线l的对称点N(与M不重合)在椭圆Γ上,求t
的值;
(3)设P(-3,0),直线PA与椭圆Γ的另一个交点为C,直线PB与椭圆Γ的另一个交点为D,若点
7 1
C,D和点Q- ,
3 2
58
三点共线,求k的值.
解析:(1)设椭圆的焦距为2c,
x2 y2 2 5
因为椭圆Γ: + =1(a>b>0)的长轴长为2 5,离心率为 ,
a2 b2 5
c 2 5
所以a= 5, = ,所以c=2,
a 5
所以b2=a2-c2=5-4=1.
x2
故椭圆Γ的方程为 +y2=1.
5
(2)设点M(0,1)关于直线l的对称点为N(s,n),
n+1 s
2 = 2 +t s=1-t
则
n-1
,解得
n=t
,则N(1-t,t),
=-1
s
(1-t)2
由N在椭圆P上,可得 +t2=1,
5
2
整理得3t2-t-2=0,解得t=1或t=- .
3
当t=1时,点N(0,1)与点M重合,舍去,
2 5 2
当t=- 时,点N ,-
3 3 3
,满足要求.
(3)设A(x,y),B(x ,y ),C(x ,y ),D(x ,y ),则x2+5y2=5,x2+5y2=5.
1 1 2 2 3 3 4 4 1 1 2 2
y
又P(-3,0),设PA的斜率为k,则k = 1 ,直线PA的方程为y=k(x+3),
1 1 x +3 1
1
y=k(x+3)
1
由 x2 消去y并整理得(1+5k2 1 )x2+30k2 1 x+45k2 1 -5=0,
+y2=1
5
30k2 30k2
则x +x =- 1 ,所以x =- 1 -x.
1 3 1+5k2 3 1+5k2 1
1 1
y
30 1
y x +3
又k = 1 ,所以x =- 1
1 x +3 3
1
2
y
1+5 1
x +3
1
14x +30 7x +15
-x =- 1 =- 1 ,
2 1 6x +14 3x +7
1 1
2y 7x +15 2y
所以y =k(x +3)= 1 ,则C- 1 , 1
3 1 3 3x +7 3x +7 3x +7
1 1 1
,7x +15 2y
同理可求得D- 2 , 2
3x +7 3x +7
2 2
圆锥曲线黄金55题 59
7 1
.又Q- ,
3 2
,
7x +15 7 2y 1
则QC=- 1 + , 1 -
3x +7 3 3x +7 2
1 1
4 2y 1
= , 1 -
3(3x +7) 3x +7 2
1 1
,
7x +15 7 2y 1
QD=- 2 + , 2 -
3x +7 3 3x +7 2
2 2
4 2y 1
= , 2 -
3(3x +7) 3x +7 2
2 2
.
7 1
由点C,D和点Q- ,
3 2
三点共线,所以QC∥QD,
4 2y 1
则 2 -
3(3x +7) 3x +7 2
1 2
4 2y 1
- 1 -
3(3x +7) 3x +7 2
2 1
=0,
3 y -y 3
可得y -y = (x -x),则k= 2 1 = .
2 1 4 2 1 x -x 4
2 1y2
52 已知双曲线C:x2- =1的左、右焦点分别为F、F,P为双曲线右支上一点.
3 1 2
(1)求双曲线C的离心率;
(2)设过点P和F 的直线l与双曲线C的右支有另一交点为Q,求OP⋅OQ的取值范围;
2
(3)过点P分别作双曲线C两条渐近线的垂线,垂足分别为M、N两点,是否存在点P,使得|PM|
+|PN|= 2?若存在,求出点P的坐标,若不存在,请说明理由.
解析:(1)由题意知,a2=1,b2=3,则c2=a2+b2=4,
c
所以c=2,a=1,得e= =2,
a
即双曲线的离心率为2;
(2)由(1)知,F(2,0),
2
若直线l的斜率为0,则直线l与双曲线的两个交点分布在左、右支各一点,不符合题意:
所以直线l的斜率不为0,设l:x=my+2,P(x,y),Q(x ,y ),
1 1 2 2
x=my+2
联立直线与双曲线方程得 y2 ,消去x得,(3m2-1)y2+12my+9=0,
x2- =1
3
Δ=(12m)2-36(3m2-1)=36m2+36>0,
12m 9
y +y =- ,yy = ,
1 2 3m2-1 1 2 3m2-1
则xx =(my +2)(my +2)=m2yy +2m(y +y )+4
1 2 1 2 1 2 1 2
9m2 24m2 -3m2-4
= - +4= ,
3m2-1 3m2-1 3m2-1
-3m2-4 9 -3m2+5 4
所以OP⋅OQ=xx +yy = + = =-1+ ,
1 2 1 2 3m2-1 3m2-1 3m2-1 3m2-1
9
又 yy = <0,则 3m2-1<0,
1 2 3m2-1
由 3m2≥0,得3m2-1≥-1,
4 4
所以-1≤3m2-1<0,有 ≤-4,所以-1+ ≤-5,
3m2-1 3m2-1
即OP⋅OQ≤-5,所以OP⋅OQ的取值范围为(-∞,-5];
(3)由题意可知双曲线的渐近线方程为l:y= 3x,l :y=- 3x,
1 2
即l: 3x-y=0,l : 3x+y=0,设P(x ,y ),
1 2 0 0
因为点P在双曲线的右支上,则x ≥1,
0
| 3x -y | | 3x +y |
则点P到直线l 的距离为|PM|= 0 0 ,点P到直线l 的距离为|PN|= 0 0 ,
1 2 2 2
| 3x -y | | 3x +y | | 3x -y + 3x +y |
所以|PM|+|PN|= 0 0 + 0 0 ≥ 0 0 0 0 = 3x ≥ 3,
2 2 2 0
故不存在点P使得|PM|+|PN|= 2.
60x2 y2 2
53 椭圆E: + =1(a>b>0)的离心率是 ,点M( 2,1)是椭圆E上一点,过点P(0,
a2 b2 2
1)的动直线l与椭圆相交于A,B两点.
(1)求椭圆E的方程;
(2)求△AOB面积的最大值;
|QA| |PA|
(3)在平面直角坐标系xOy中,是否存在与点P不同的定点Q,使 = 恒成立?存在,求
|QB| |PB|
出点Q的坐标;若不存在,请说明理由.
c = 2
a 2
x2 y2
解析:(1)根据题意,得 a2=b2+c2 ,解得a2=4,b2=2,c2=2,椭圆C的方程为 + =1;
4 2
2 1
+ =1
a2 b2
y=kx+1
(2)依题意,设A(x 1 ,y 1 ),B(x 2 ,y 2 ),设直线l为y=kx+1,联立 x2 y2 ,消去y,
+ =1
4 2
4k 2
得(1+2k2)x2+4kx-2=0,Δ>0恒成立,x +x =- ,xx =- ,
1 2 1+2k2 1 2 1+2k2
1 1 1 4k
所 以 S = | x - x | = (x +x )2-4xx = -
△AOB 2 1 2 2 1 2 1 2 2 1+2k2
圆锥曲线黄金55题 61
2 2
-4-
1+2k2
=
2 1+4k2
,
1+2k2
2t 2
令t= 1+4k2,t≥1,S = 2• = 2• ≤ 2,
△AOB t2+1 1
t+
t
当且仅当t=1,即k=0时取得等号,综上可知,△AOB面积的最大值为 2;
|QA| |PA|
(3)结论:存在与点P不同的定点Q(0,2),使得 = 恒成立.理由如下:
|QB| |PB|
当直线l与x轴平行时,设直线l与椭圆相交于C、D两点,
|QC| |PC|
如果存在定点Q满足条件,则有 = =1,即|QC|=|QD|,
|QD| |PD|
∴Q点在直线y轴上,可设Q(0,y ),
0
当直线l与x轴垂直时,设直线l与椭圆相交于M、N两点,如果存在定点Q满足条件,
|QM| |PM| |y - 2| 2-1
则 = ,即 0 = ,解得y =1或y =2,
|QN| |PN| |y + 2| 2+1 0 0
0
∴若存在不同于点P的定点Q满足条件,则Q点坐标只能是(0,2);
当直线l不平行于x轴且不垂直与x轴时,可设直线l的方程为y=kx+1,y=kx+1
联立 x2 y2 ,消去y并整理得:(1+2k2)x2+4kx-2=0,
+ =1
4 2
∵Δ=(4k)2+8(1+2k2)>0,
4k 2
∴x +x =- ,xx =- ,
1 2 1+2k2 1 2 1+2k2
又点B关于y轴对称的点B′的坐标为(-x ,y ),
2 2
y -2 kx -1 1 y -2 kx -1 1
又k = 1 = 1 =k- ,k = 2 = 2 =-k+ ,
AQ x x x QB′ -x -x x
1 1 1 2 2 2
x +x
k -k =2k- 1 2 =0
AQ QB′ xx
1 2
|QA| |QA| |x| |PA|
∴k =k 则Q、A、B′三点共线,∴ = = 1 = ;
AQ QB′ |QB| |QB′| |x | |PB|
2
|QA| |PA|
故存在与点P不同的定点Q(0,2),使得 = 恒成立.
|QB| |PB|
6254 已知动圆过点F(0,1),且与直线l:y=-1相切,设动圆圆心D的轨迹为曲线C.
(1)求曲线C的方程;
(2)过l上一点P作曲线C的两条切线PA,PB,A,B为切点,PA,PB与x轴分别交于M,N两
点.记△AFM,△PMN,△BFN的面积分别为S、S 、S .
1 2 3
(ⅰ)证明:四边形FNPM为平行四边形;
S2
(ⅱ)求 2 的值.
SS
1 3
解析:(1)设圆心D(x,y),由题意得: x2+(y-1)2=|y+1|,
化简整理得:x2=4y,所以曲线C的方程为:x2=4y.
x2 x
(2)(ⅰ)设A(x,y),B(x ,y ),因为y= ,所以y′= ,
1 1 2 2 4 2
x 1 1 x
∴直线PA的方程为:y= 1 (x-x)+y,即y= xx- x2,令y=0,得到x= 1 ,
2 1 1 2 1 4 1 2
1 1 x
同理可得直线PB的方程为:y= x x- x2,令y=0,得到x= 2 ,
2 2 4 2 2
x
∴M 1 ,0
2
圆锥曲线黄金55题 63
x
,N 2 ,0
2
1 1
y= 2 x 1 x- 4 x2 1 x +x
,联立 ,消y解得x= 1 2 ,
1 1 2
y= x x- x2
2 2 4 2
x +x
所以P 1 2 ,-1
2
x
,又F(0,1),∴FM +FN = 1 ,-1
2
x
+ 2 ,-1
2
x +x
= 1 2 ,-2
2
=FP,
所以四边形FNPM为平行四边形;
1 1
(ⅱ)由(ⅰ)知直线PA的方程为y= xx- x2,又x2=4y,
2 1 4 1 1 1
1
所以 xx-y-y =0,即xx-2y-2y =0,同理可知直线PB的方程为x x-2y-2y =0,
2 1 1 1 1 2 2
xx -2y +2=0
1 0 1
又P在直线PA,PB上,设P(x
0
,-1),则 ,
x x -2y +2=0
2 0 2
所以直线AB的方程为:x x-2y+2=0,故直线AB过点F(0,1),
0
∵四边形FNPM为平行四边形,∴FM∥BP,FN∥AP,
BN BF MP
∴FN=PM,PN=MF, = = ,
NP FA MA
∴MP•NP=MA•BN,
1 1 1
∵S = |MA||MF|sin∠AMF,S = |PM||PN|sin∠MPN,S = |NB‖NF|sin∠BNF,
1 2 2 2 3 2
1
|PM||PN|sin∠MPN S2 2
∴ 2 =
SS
1 3
2
1
|MA||MF|sin∠AMF
2
1
⋅ |NB‖NF|sin∠BNF
2
(|PM|⋅|PN|)2
= =
|MA|⋅|MF|⋅|NB|⋅|NF|
|PM|⋅|PN|
=1.
|MA|⋅|NB|x2 y2
55 已知椭圆C: + =1(a>b>0)的一条准线方程为x=4,长轴长为4,过点P(-2,1)
a2 b2
作直线l交椭圆C于点M、N.
(1)求椭圆C的方程;
1 1
(2)在x轴上是否存在一定点Q,使得直线QM,QN的斜率k ,k 满足 + 为常数?若存在,
1 2 k k
1 2
求出Q点坐标;若不存在,说明理由.
a2 =4
c a=2
解析:(1)有题意可知,
a=4
⇒
b2=3
,
a2=b2+c2
x2 y2
所以椭圆C的方程为 + =1;
4 3
(2)假设存在满足条件的点Q(t,0),当直线l与x轴垂直时,它与椭圆只有一个交点,不满足题意;
所以直线l的斜率k存在,设直线l的方程为y-1=k(x+2),点M(x,y),N(x ,y ),
1 1 2 2
y-1=k(x+2)
联立为 ,得(3+4k2)x2+(16k2+8k)x+16k2+16k-8=0,
3x2+4y2=12
16k2+8k 16k2+16k-8
则x +x =- ,xx = ,
1 2 3+4k2 1 2 3+4k2
y y
1 + 2
1 1 k +k x -t x -t y(x -t)+y (x -t)
+ = 1 2 = 1 2 = 1 2 2 1
k k kk y y yy
1 2 1 2 1 ⋅ 2 1 2
x -t x -t
1 2
(kx +2k+1)(x -t)+(kx +2k+1)(x -t)
= 1 2 2 1
(kx +2k+1)(kx +2k+1)
1 2
2kxx +(2k+1-kt)(x +x )-2(2k+1)t (-12t-24)k-6t
= 1 2 1 2 = .
k2xx +(2k2+k)(x +x )+4k2+4k+1 12k+3
1 2 1 2
1 1 -12t-24 -6t
要使 + 为定值,则需满足 = .解得t=2.
k k 12 3
1 2
1 1 -48k-12
此时, + = =-4.
k k 12k+3
1 2
1 1
所以在x轴上存在点Q(2,0),使得 + 为定值-4.
k k
1 2
64