四川省南充高级中学2024-2025高二上学期期中考试数学试题_2024-2025高二（7-7月题库）_2024年11月试卷_1128四川省南充高级中学2024-2025学年高二上学期期中考试

     5  南充高中 2024—2025 学年度上学期期中考试 7．如图， 函数 f(x)2sin(x)0, 的图象经过点 ,0和 ,0， 则下列说  2  12  12  高 2023 级数学试卷 法错误的是（ ） ．． A．2 （时间：120分钟 总分：150分 命审题人：向前君 蔡国良 李波 杨秦飞）  B． 6 一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是   6 3 C．若 f     ， 则cos2 符合题目要求的．  6  5 5 1．已知圆C的方程是x2  y2 4x2y110，则圆心C的坐标是（ ） D．函数 f (x)的图象与直线8x5y100仅有三个公共点 1 1 3 A．2,1 B．2,1 C．4,2 D．4,2 8．已知ABC的内角A,B,C的对边分别为a，b，c，若   ，则cosB的最 tanA tanC tanB   小值为（ ） 2．已知向量a (1,4,5)，b (0,1,2)，则a 2b （ ） 1 1 3 2 A．(1,6,1) B．(1,6,9) C．(1,6,1) D．(1,6,1) A． B． C． D． 2 9 2 5 3．设直线l的方程为 3x y3 0，则下列向量可以作为l方向向量的是（ ） 二、多选题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目 要求．全部选对的得6分，部分选对的得部分分，有选错的得0分． A． 1，3  B． 1， 3  C． 3，1  D． 3，1  9．民营经济是推进中国式现代化的生力军．为了更好地支持民营企业的发展，某市决定对部分 4．已知集合A x,y x2  y2 1  ，B   x,y  x1 2  y1 2 1  ，则AB （ ） 企业的税收进行适当的减免. 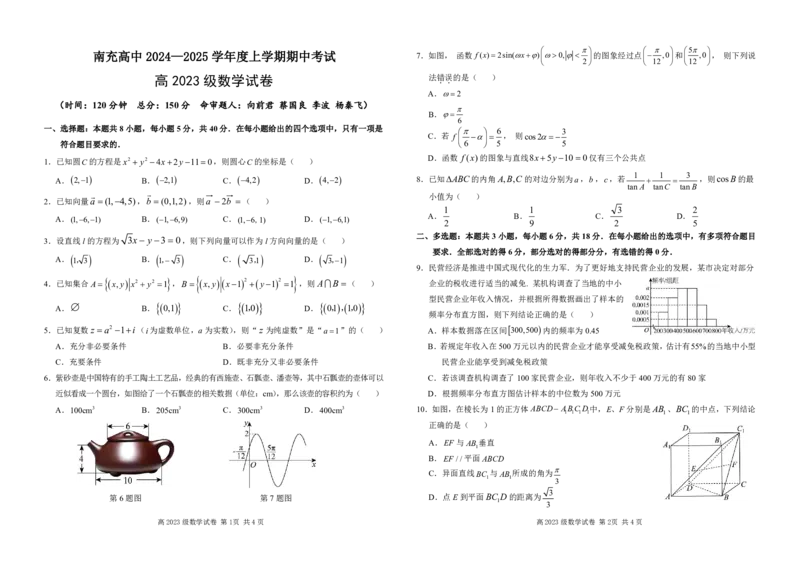某机构调查了当地的中小 型民营企业年收入情况，并根据所得数据画出了样本的 A． B．  0,1  C．  1，0  D．  0，1 ， 1，0  频率分布直方图，则下列结论正确的是（ ） 5．已知复数z a2 1i（i为虚数单位，a为实数），则“z 为纯虚数”是“a1”的（ ） A．样本数据落在区间 300,500内的频率为0.45 A．充分非必要条件 B．必要非充分条件 B．若规定年收入在500万元以内的民营企业才能享受减免税政策，估计有55%的当地中小型 C．充要条件 D．既非充分又非必要条件 民营企业能享受到减免税政策 6．紫砂壶是中国特有的手工陶土工艺品，经典的有西施壶、石瓢壶、潘壶等，其中石瓢壶的壶体可以 C．若该调查机构调查了100家民营企业，则年收入不少于400万元的有80家 近似看成一个圆台，如图给了一个石瓢壶的相关数据（单位：cm），那么该壶的容积约为（ ） D．根据频率分布直方图估计样本的中位数为500万元 A．100cm3 B．205cm3 C．300cm3 D．400cm3 10．如图，在棱长为1的正方体ABCD ABCD中，E、F分别是AB 、BC 的中点，下列结论 1 1 1 1 1 1 正确的是（ ） A．EF与AB垂直 1 B．EF //平面ABCD  C．异面直线BC 与AB所成的角为 1 1 3 3 第6题图 第7题图 D．点E到平面BC D的距离为 1 3 高2023级数学试卷 第1页 共4页 高2023级数学试卷 第2页 共4页11．已知动点 P 在直线l:x y60上，动点Q在圆C:x2y22x2y20上，过点 P 作圆 17.（满分15分） C的两条切线，切点分别为A、B，则下列描述正确的有（ ） 甲、乙两人组队成“星对”参加猜成语活动，每轮活动由甲、乙各猜一个成语，已知甲每轮 A．直线l与圆C相交 B． PQ 的最小值为2 22 猜对的概率为 p ，乙每轮猜对的概率为 p ，在每轮活动中，甲和乙猜对与否互不影响，各轮结 1 2  1 1 C．存在P点，使得APB D．直线AB过定点(2，2) 果也互不影响。在一轮活动中，甲、乙都猜对的概率为 ，甲猜对且乙猜错的概率为 ． 2 2 4 三、填空题：本题共3小题，每小题5分，共15分． （1）求 p 1 ， p 2 的值； （2）求“星队”在两轮活动中猜对3个成语的概率． 12．与直线2x y20平行，且在 y 轴上的截距为1的直线的一般式方程是 ． 13．某企业为了推广一种新饮料，开展了有奖促销活动：将6罐这种饮料装一箱，每箱中都放 置2罐能够中奖的饮料，若从一箱中随机抽出2罐饮料，恰好一罐中奖另一罐不中奖的概率 为 ． 18.（满分17分）               在ABC中，角A,B,C所对的边分别为a，b，c，且满足2ba 2ccosA，ABC的外 14．已知a,b,c 为平面向量，如果 c 1，a,c  ，b b 6c 8，则 ab  ac 的 3 接圆的半径为R=1． 最小值为 ． （1）求角C的值； 四、解答题：本题共5小题，共77分．解答应写出文字说明、证明过程或演算步骤． （2）如果2sin AsinB，求ABC的面积； 15.（满分13分） （3）求内切圆半径r的最大值． 已知直线l:  21  x1  y740． （1）求证：不论实数取何值，直线l恒过一定点P； （2）在（1）的条件下，若直线l与x轴相交于点A，与y轴相交于点B，且P恰为线段AB的中 19.（满分17分） 点，求直线l的斜截式方程． 常用测量距离的方式有3种，设A  x ,y ，B  x ,y ，定义欧几里得距离 1 1 2 2 D  A,B    x x 2   y  y 2 ；定义曼哈顿距离M  A,B   x x  y  y ；定义余弦距 1 2 1 2 1 2 1 2 16.（满分15分） 离e  A,B  1cos  A,B  ，其中cos  A,B  cosOA,OB (O为坐标原点). 如图，在四棱锥ABCDE中，AC 平面BCDE，BCD90，DE//BC，且DECDCA2， （1）若A  1，2 ，B  1，2 ，求A,B之间的余弦距离e  A,B  ； BC 4，M 是AD的中点，N是AB的中点．    3 （1）求证：CM 平面ADE； （2）若C 4xx2,x2 ，D  1，  ，求e  C,D  的取值范围；  3  （2）求平面ADE与平面DEN所成夹角的余弦值． （3）动点P在直线 y  x2上，动点Q在圆x2  y2 1上，求M  P,Q  的最小值． 高2023级数学试卷 第3页 共4页 高2023级数学试卷 第4页 共4页