专题07直线与圆（3大考向真题解读）-解析版_2024-2025高三（6-6月题库）_2024年08月试卷_08202025版《真题题源解密-专题分类》数学

专题 07 直线与圆 命题解读 考向 考查统计 1.高考对直线的考查，重点是直线的倾 2023·新高考Ⅰ卷，6 斜角与斜率、直线方程的求法、两条直 2022·新高考Ⅱ卷，15 线的位置关系、距离公式、对称问题等。 直线与圆的位置关系 2023·新高考Ⅱ卷，15 2.高考对圆的考查，重点是圆的标准方 2024·新高考Ⅱ卷，10（多 程与一般方程的求法，除了待定系数法 选题的一个选项中考查） 外，要特别要重视利用几何性质求解圆 圆与圆的位置关系 2022·新高考Ⅰ卷，14 的方程。同时，除了直线与圆、圆与圆 的位置关系的判断，还特别要重视直线 与圆相交所得弦长及相切所得切线的 直线的斜率 2022·新高考Ⅱ卷，3 问题。 3.其他就是直线、圆与其他知识点的交 汇。 命题分析 2024(cid:3)(cid:4)(cid:5)(cid:6)(cid:4)(cid:5)Ⅰ(cid:7)(cid:8)(cid:9)(cid:10)(cid:5)(cid:11)(cid:9)(cid:12)(cid:13)(cid:14)(cid:15)(cid:16)(cid:17)(cid:18)(cid:19)(cid:20)(cid:21)Ⅱ(cid:7)(cid:22)(cid:23)(cid:24)(cid:25)(cid:15)(cid:26)(cid:27)(cid:24)(cid:28)(cid:29)(cid:5)(cid:30)(cid:31)(cid:9)(cid:12)(cid:13)(cid:14) (cid:16)(cid:32)(cid:15)(cid:33)(cid:25)(cid:21)(cid:34)(cid:35)(cid:22)(cid:36)(cid:37)(cid:25)(cid:29)(cid:38)(cid:39)(cid:9)(cid:12)(cid:40)(cid:41)(cid:15)(cid:42)(cid:43)(cid:21)(cid:44)(cid:45)(cid:46)(cid:25)(cid:47)(cid:48)(cid:49)(cid:50)(cid:34)(cid:35)(cid:9)(cid:12)(cid:13)(cid:14)(cid:9)(cid:10)(cid:5)(cid:11)(cid:15)(cid:51)(cid:21)(cid:52)(cid:53) (cid:26)(cid:54)(cid:55)(cid:56)(cid:57)(cid:15)(cid:21)(cid:26)(cid:54)(cid:58)(cid:59)(cid:60)(cid:61)(cid:62)(cid:63)(cid:64)(cid:50)(cid:22)(cid:26)(cid:65)(cid:66)(cid:52)(cid:53)(cid:15)(cid:25)(cid:67)(cid:29)(cid:21)(cid:68)(cid:68)(cid:39)(cid:9)(cid:12)(cid:40)(cid:41)(cid:15)(cid:26)(cid:65)(cid:42)(cid:43)(cid:50)(cid:9)(cid:12)(cid:13)(cid:14)(cid:5) (cid:11)(cid:69)(cid:17)(cid:70)(cid:71)(cid:9)(cid:12)(cid:72)(cid:14)(cid:15)(cid:73)(cid:74)(cid:75)(cid:76)(cid:77)(cid:17)(cid:78)(cid:21)(cid:9)(cid:12)(cid:73)(cid:74)(cid:15)(cid:79)(cid:80)(cid:72)(cid:9)(cid:12)(cid:81)(cid:82)(cid:20)(cid:33)(cid:25)(cid:15)(cid:79)(cid:80)(cid:72)(cid:83)(cid:84)(cid:9)(cid:12)(cid:73)(cid:74)(cid:29)(cid:84)(cid:85) (cid:86)(cid:87)(cid:88)(cid:89)(cid:79)(cid:80)(cid:72)(cid:9)(cid:12)(cid:13)(cid:14)(cid:15)(cid:76)(cid:77)(cid:17)(cid:78)(cid:29)(cid:90)(cid:75)(cid:15)(cid:91)(cid:92)(cid:13)(cid:32)(cid:12)(cid:73)(cid:74)(cid:15)(cid:79)(cid:80)(cid:50)(cid:93)(cid:94)(cid:95)(cid:25)(cid:67)(cid:72)(cid:94)(cid:95)(cid:80)(cid:96)(cid:97)(cid:98)(cid:99)(cid:73)(cid:100)(cid:21) (cid:94)(cid:101)(cid:102)(cid:103)(cid:104)(cid:60)(cid:105)(cid:106)(cid:72)(cid:107)(cid:85)(cid:72)(cid:108)(cid:109)(cid:110)(cid:111)(cid:112)(cid:105)(cid:18)(cid:19)(cid:5)(cid:11)(cid:113)(cid:87)(cid:33)(cid:25)(cid:50)(cid:114)(cid:58)2025(cid:3)(cid:4)(cid:5)(cid:115)(cid:55)(cid:98)(cid:99)(cid:5)(cid:11)(cid:9)(cid:12)(cid:13)(cid:14)(cid:15)(cid:76) (cid:77)(cid:17)(cid:78)(cid:50) 试题精讲 (cid:22)(cid:23)(cid:24)(cid:20)(cid:21) 1(cid:25)(cid:26)2024(cid:27)(cid:28)(cid:29)Ⅱ(cid:30)·10(cid:31)(cid:32)(cid:14)(cid:33)C(cid:10)y2 =4x(cid:34)(cid:35)(cid:33)(cid:36)l(cid:37)P(cid:36)C(cid:38)(cid:34)(cid:39)(cid:40)(cid:37)(cid:41)P(cid:42)(cid:43)A:x2(y4)2 =1(cid:34) (cid:22)(cid:44)(cid:45)(cid:33)(cid:37)Q(cid:36)(cid:45)(cid:40)(cid:37)(cid:41)P(cid:42)l(cid:34)(cid:46)(cid:33)(cid:37)(cid:46)(cid:47)(cid:36)B(cid:37)(cid:48)(cid:26) (cid:31)A(cid:25)l(cid:49)eA(cid:50)(cid:45) B(cid:25)(cid:51)P(cid:37)A(cid:37)B(cid:52)(cid:40)(cid:53)(cid:33)(cid:54)(cid:37)|PQ|= 15 C(cid:25)(cid:51)|PB|=2(cid:54)(cid:37)PA^ AB D(cid:25)(cid:55)(cid:47)|PA|=|PB|(cid:34)(cid:40)P(cid:56)(cid:57)(cid:58)(cid:56)2(cid:59) (cid:60)(cid:61)(cid:62)(cid:63)ABD (cid:60)(cid:64)(cid:65)(cid:63)A(cid:20)(cid:66)(cid:37)(cid:32)(cid:14)(cid:33)(cid:35)(cid:33)(cid:36)x=1(cid:37)(cid:67)(cid:68)(cid:69)(cid:70)(cid:71)(cid:35)(cid:33)(cid:34)(cid:72)(cid:73)(cid:74)(cid:75)(cid:76)(cid:77)B(cid:20)(cid:66)(cid:37)P,A,B(cid:52)(cid:40)(cid:53)(cid:33)(cid:54)(cid:37)(cid:78)(cid:79) (cid:80)P(cid:34)(cid:81)(cid:82)(cid:37)(cid:83)(cid:84)(cid:85)(cid:80)(cid:45)(cid:33)(cid:86)(cid:77)C(cid:20)(cid:66)(cid:37)(cid:67)(cid:68) PB =2(cid:78)(cid:87)(cid:80)P(cid:34)(cid:81)(cid:82)(cid:37)(cid:88)(cid:89)(cid:90)(cid:91)k k =1(cid:92)(cid:93)(cid:94)(cid:95)(cid:77)D PA AB (cid:20)(cid:66)(cid:37)(cid:67)(cid:68)(cid:32)(cid:14)(cid:33)(cid:34)(cid:96)(cid:97)(cid:37) PB = PF (cid:37)(cid:98)(cid:92)(cid:99)(cid:21)(cid:100)(cid:16)(cid:94) PA = PF (cid:34)P(cid:40)(cid:34)(cid:101)(cid:102)(cid:103)(cid:99)(cid:21)(cid:37)(cid:104)(cid:54)(cid:29)(cid:105)AF(cid:34)(cid:106) (cid:46)(cid:33)(cid:107)(cid:32)(cid:14)(cid:33)(cid:34)(cid:108)(cid:40)(cid:59)(cid:13)(cid:109)(cid:110)(cid:37)(cid:111)(cid:110)(cid:112)(cid:113)(cid:114)P(cid:40)(cid:81)(cid:82)(cid:83)(cid:115)(cid:79)(cid:116). (cid:60)(cid:117)(cid:116)(cid:63)A(cid:20)(cid:66)(cid:37)(cid:32)(cid:14)(cid:33)y2 =4x(cid:34)(cid:35)(cid:33)(cid:36)x=1(cid:37) eA(cid:34)(cid:69)(cid:70)(0,4)(cid:71)(cid:112)(cid:33)x=1(cid:34)(cid:72)(cid:73)(cid:118)(cid:88)(cid:92)1(cid:37)(cid:119)(cid:98)(cid:69)(cid:34)(cid:120)(cid:121)(cid:37) (cid:122)(cid:35)(cid:33)l(cid:107)eA(cid:50)(cid:45)(cid:37)A(cid:20)(cid:66)(cid:123)(cid:124)(cid:77) (cid:22)(cid:23)(cid:125)(cid:20)(cid:21) 1(cid:25)(cid:26)2023(cid:27)(cid:28)(cid:29)Ⅰ(cid:30)·6(cid:31)(cid:41)(cid:40)0,2(cid:49)(cid:69)x2y24x1=0(cid:50)(cid:45)(cid:34)(cid:126)(cid:44)(cid:112)(cid:33)(cid:34)(cid:127)(cid:128)(cid:36)a(cid:37)(cid:48)sina=(cid:26) (cid:31) 15 10 6 A(cid:25)1 B(cid:25) C(cid:25) D(cid:25) 4 4 4 (cid:60)(cid:61)(cid:62)(cid:63)B (cid:60)(cid:64)(cid:65)(cid:63)(cid:129)(cid:130)(cid:22)(cid:10)(cid:67)(cid:68)(cid:45)(cid:33)(cid:34)(cid:103)(cid:131)(cid:79)(cid:45)(cid:33)(cid:86)(cid:37)(cid:132)(cid:133)(cid:134)(cid:128)(cid:7)(cid:135)(cid:136)(cid:87)(cid:79)(cid:116)(cid:77)(cid:129)(cid:130)(cid:137)(cid:10)(cid:67)(cid:68)(cid:45)(cid:33)(cid:34)(cid:103)(cid:131)(cid:79)(cid:45)(cid:33)(cid:86)(cid:37) (cid:132)(cid:133)(cid:138)(cid:139)(cid:96)(cid:15)(cid:136)(cid:87)(cid:79)(cid:116)(cid:77)(cid:129)(cid:130)(cid:52)(cid:10)(cid:67)(cid:68)(cid:45)(cid:33)(cid:132)(cid:133)(cid:40)(cid:71)(cid:112)(cid:33)(cid:34)(cid:72)(cid:73)(cid:7)(cid:135)(cid:110)(cid:85)k28k1=0(cid:37)(cid:140)(cid:141)(cid:142)(cid:143)(cid:96)(cid:15)(cid:132) (cid:133)(cid:127)(cid:128)(cid:7)(cid:135)(cid:136)(cid:87)(cid:79)(cid:116). (cid:60)(cid:117)(cid:116)(cid:63)(cid:129)(cid:130)(cid:22)(cid:10)(cid:144)(cid:36)x2y24x1=0(cid:37)(cid:109)x22y2 =5(cid:37)(cid:110)(cid:85)(cid:69)(cid:70)C2,0(cid:37)(cid:120)(cid:121)r= 5(cid:37) (cid:41)(cid:40)P0,2(cid:42)(cid:69)C(cid:34)(cid:45)(cid:33)(cid:37)(cid:45)(cid:40)(cid:36)A,B(cid:37) (cid:144)(cid:36) PC = 2222 =2 2(cid:37)(cid:48) PA = PC 2r2 = 3(cid:37) 5 10 3 6 (cid:110)(cid:85)sinÐAPC = = ,cosÐAPC = = (cid:37) 2 2 4 2 2 4 10 6 15 (cid:48)sinÐAPB=sin2ÐAPC =2sinÐAPCcosÐAPC =2´ ´ = (cid:37) 4 4 4 2 2 æ 6ö æ 10ö 1 cosÐAPB=cos2ÐAPC =cos2ÐAPCsin2ÐAPC =ç ÷ ç ÷ = <0(cid:37) ç ÷ ç ÷ è 4 ø è 4 ø 4(cid:109)ÐAPB(cid:36)(cid:145)(cid:128)(cid:37) 15 (cid:146)(cid:147)sina=sinπÐAPB=sinÐAPB= (cid:77) 4 (cid:130)(cid:137)(cid:10)(cid:69)x2y24x1=0(cid:34)(cid:69)(cid:70)C2,0(cid:37)(cid:120)(cid:121)r= 5(cid:37) (cid:41)(cid:40)P0,2(cid:42)(cid:69)C(cid:34)(cid:45)(cid:33)(cid:37)(cid:45)(cid:40)(cid:36)A,B(cid:37)(cid:148)(cid:113)AB(cid:37) (cid:110)(cid:85) PC = 2222 =2 2(cid:37)(cid:48) PA = PB = PC 2r2 = 3(cid:37) (cid:144)(cid:36) PA 2 PB 22 PA× PB cosÐAPB= CA 2 CB 22CA×CB cosÐACB (cid:57)ÐACB=πÐAPB(cid:37)(cid:48)336cosÐAPB=5510cosπÐAPB(cid:37) 1 (cid:109)3cosÐAPB=55cosÐAPB(cid:37)(cid:116)(cid:85)cosÐAPB= <0(cid:37) 4 1 (cid:109)ÐAPB(cid:36)(cid:145)(cid:128)(cid:37)(cid:48)cosa=cosπÐAPB=cosÐAPB= (cid:37) 4 15 (cid:57)a(cid:36)(cid:149)(cid:128)(cid:37)(cid:146)(cid:147)sina= 1cos2a= (cid:77) 4 (cid:129)(cid:130)(cid:52)(cid:10)(cid:69)x2y24x1=0(cid:34)(cid:69)(cid:70)C2,0(cid:37)(cid:120)(cid:121)r= 5(cid:37) (cid:150)(cid:45)(cid:33)(cid:151)(cid:152)(cid:153)(cid:101)(cid:102)(cid:37)(cid:48)(cid:45)(cid:33)(cid:129)(cid:154)(cid:36)x=0(cid:37)(cid:48)(cid:69)(cid:70)(cid:71)(cid:45)(cid:40)(cid:34)(cid:72)(cid:73)d =2>r(cid:37)(cid:153)(cid:133)(cid:21)(cid:155)(cid:77) (cid:150)(cid:45)(cid:33)(cid:151)(cid:152)(cid:101)(cid:102)(cid:37)(cid:114)(cid:45)(cid:33)(cid:129)(cid:154)(cid:36)y=kx2(cid:37)(cid:109)kxy2=0(cid:37) 2k2 (cid:48) = 5(cid:37)(cid:156)(cid:15)(cid:85)k28k1=0(cid:37)(cid:57)D=644=60>0 k21 (cid:114)(cid:126)(cid:45)(cid:33)(cid:151)(cid:152)(cid:64)(cid:157)(cid:36)k,k (cid:37)(cid:48)k k =8,kk =1(cid:37) 1 2 1 2 1 2 (cid:110)(cid:85) k k = k k 24kk =2 15(cid:37) 1 2 1 2 1 2 k k sina sina (cid:146)(cid:147)tana= 1 2 = 15(cid:37)(cid:109) = 15(cid:37)(cid:110)(cid:85)cosa= (cid:37) 1kk cosa 15 1 2 sin2a (cid:48)sin2acos2a=sin2a =1(cid:37) 15 (cid:57)aÎ0,π(cid:37)(cid:48)sina>0(cid:37)(cid:116)(cid:85)sina= 15 . 4 (cid:122)(cid:20)(cid:10)B. 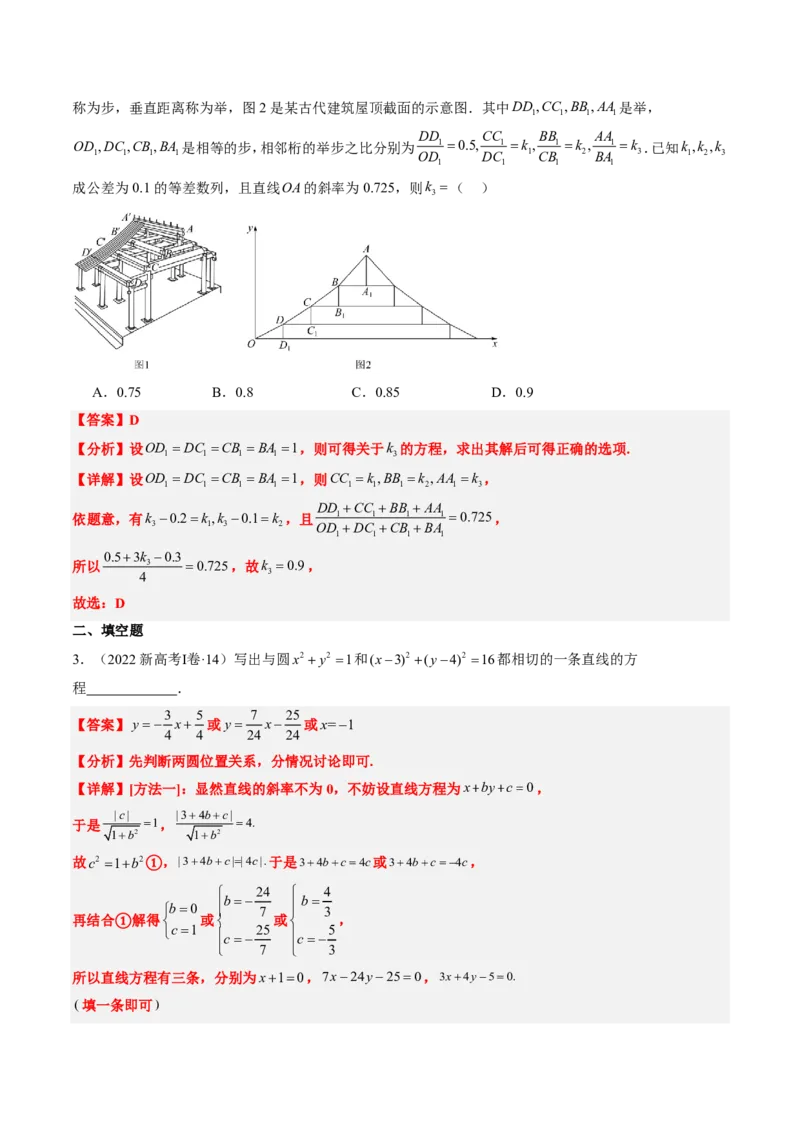2(cid:25)(cid:26)2022(cid:27)(cid:28)(cid:29)Ⅱ(cid:30)·3(cid:31)(cid:158)1(cid:92)(cid:106)(cid:159)(cid:160)(cid:161)(cid:162)(cid:163)(cid:106)(cid:34)(cid:164)(cid:165)(cid:132)(cid:166)(cid:37)AA¢,BB¢,CC¢,DD¢(cid:92)(cid:167)(cid:37)(cid:50)(cid:168)(cid:167)(cid:34)(cid:169)(cid:170)(cid:72)(cid:73)(cid:171)(cid:36)(cid:172)(cid:37)(cid:46)(cid:112)(cid:72)(cid:73)(cid:171)(cid:36)(cid:164)(cid:37)(cid:158)2(cid:92)(cid:173)(cid:160)(cid:161)(cid:162)(cid:163)(cid:174)(cid:175)(cid:176)(cid:177)(cid:34)(cid:178)(cid:155)(cid:158)(cid:25)(cid:179)(cid:106)DD,CC,BB,AA (cid:92)(cid:164)(cid:37) 1 1 1 1 DD CC BB AA OD,DC,CB,BA (cid:92)(cid:50)(cid:119)(cid:34)(cid:172)(cid:37)(cid:50)(cid:168)(cid:167)(cid:34)(cid:164)(cid:172)(cid:180)(cid:181)(cid:64)(cid:157)(cid:36) 1 =0.5, 1 =k , 1 =k , 1 =k (cid:25)(cid:182)(cid:183)k ,k ,k 1 1 1 1 OD DC 1 CB 2 BA 3 1 2 3 1 1 1 1 (cid:94)(cid:7)(cid:184)(cid:36)0.1(cid:34)(cid:119)(cid:184)(cid:13)(cid:185)(cid:37)(cid:57)(cid:112)(cid:33)OA(cid:34)(cid:151)(cid:152)(cid:36)0.725(cid:37)(cid:48)k =(cid:26) (cid:31) 3 A(cid:25)0.75 B(cid:25)0.8 C(cid:25)0.85 D(cid:25)0.9 (cid:60)(cid:61)(cid:62)(cid:63)D (cid:60)(cid:64)(cid:65)(cid:63)(cid:114)OD =DC =CB =BA =1(cid:37)(cid:48)(cid:110)(cid:85)(cid:3)(cid:98)k (cid:34)(cid:129)(cid:154)(cid:37)(cid:79)(cid:80)(cid:179)(cid:116)(cid:89)(cid:110)(cid:85)(cid:123)(cid:124)(cid:34)(cid:20)(cid:66). 1 1 1 1 3 (cid:60)(cid:117)(cid:116)(cid:63)(cid:114)OD =DC =CB =BA =1(cid:37)(cid:48)CC =k ,BB =k ,AA =k (cid:37) 1 1 1 1 1 1 1 2 1 3 DD CC BB AA (cid:186)(cid:21)(cid:155)(cid:37)(cid:56)k 0.2=k ,k 0.1=k (cid:37)(cid:57) 1 1 1 1 =0.725(cid:37) 3 1 3 2 OD DC CB BA 1 1 1 1 0.53k 0.3 (cid:146)(cid:147) 3 =0.725(cid:37)(cid:122)k =0.9(cid:37) 4 3 (cid:122)(cid:20)(cid:10)D (cid:137)(cid:23)(cid:187)(cid:188)(cid:21) 3(cid:25)(cid:26)2022(cid:27)(cid:28)(cid:29)Ⅰ(cid:30)·14(cid:31)(cid:189)(cid:80)(cid:49)(cid:69)x2y2 =1(cid:107)(x3)2(y4)2 =16(cid:190)(cid:50)(cid:45)(cid:34)(cid:22)(cid:44)(cid:112)(cid:33)(cid:34)(cid:129) (cid:154) (cid:25) 3 5 7 25 (cid:60)(cid:61)(cid:62)(cid:63)y= x (cid:191)y= x (cid:191)x=1 4 4 24 24 (cid:60)(cid:64)(cid:65)(cid:63)(cid:78)(cid:75)(cid:76)(cid:126)(cid:69)(cid:192)(cid:193)(cid:3)(cid:194)(cid:37)(cid:64)(cid:195)(cid:196)(cid:197)(cid:198)(cid:109)(cid:110). (cid:60)(cid:117)(cid:116)(cid:63)[(cid:129)(cid:130)(cid:22)](cid:10)(cid:118)(cid:88)(cid:112)(cid:33)(cid:34)(cid:151)(cid:152)(cid:153)(cid:36)0(cid:37)(cid:153)(cid:199)(cid:114)(cid:112)(cid:33)(cid:129)(cid:154)(cid:36)x+by+c=0(cid:37) |c| |34bc| (cid:98)(cid:92) =1(cid:37) =4. 1b2 1b2 (cid:122)c2 =1b2 (cid:37)|34bc|=|4c|.(cid:98)(cid:92)34bc=4c(cid:191)34bc=4c(cid:37) ① ì 24 ì 4 b= b= ìb=0 ï ï 7 ï ï 3 (cid:200)(cid:132)(cid:133) (cid:116)(cid:85)í (cid:191)í (cid:191)í (cid:37) îc=1 ï c= 25 ï c= 5 ① ïî 7 ïî 3 (cid:146)(cid:147)(cid:112)(cid:33)(cid:129)(cid:154)(cid:56)(cid:52)(cid:44)(cid:37)(cid:64)(cid:157)(cid:36)x1=0(cid:37)7x24y25=0(cid:37)3x4y5=0. ((cid:187)(cid:22)(cid:44)(cid:109)(cid:110))[(cid:129)(cid:130)(cid:137)](cid:10)(cid:114)(cid:69)x2y2 =1(cid:34)(cid:69)(cid:70)O(0,0)(cid:37)(cid:120)(cid:121)(cid:36)r =1(cid:37) 1 (cid:69)(x3)2(y4)2 =16(cid:34)(cid:69)(cid:70)C(3,4)(cid:37)(cid:120)(cid:121)r =4(cid:37) 2 (cid:48)|OC|=5=r r (cid:37)(cid:144)(cid:104)(cid:126)(cid:69)(cid:201)(cid:45)(cid:37) 1 2 (cid:202)(cid:158)(cid:203)(cid:110)(cid:183)(cid:37)(cid:53)(cid:56)(cid:52)(cid:44)(cid:112)(cid:33)(cid:204)(cid:133)(cid:44)(cid:205)(cid:37)(cid:118)(cid:88)x1=0(cid:204)(cid:133)(cid:21)(cid:155)(cid:77) (cid:206)(cid:202)(cid:129)(cid:154)(x3)2(y4)2 =16(cid:107)x2y2 =1(cid:50)(cid:207)(cid:110)(cid:85)(cid:129)(cid:154)3x4y5=0(cid:37) (cid:109)(cid:36)(cid:41)(cid:126)(cid:69)(cid:7)(cid:53)(cid:45)(cid:40)(cid:34)(cid:45)(cid:33)(cid:129)(cid:154)(cid:37) (cid:206)(cid:208)(cid:183)(cid:126)(cid:69)(cid:69)(cid:70)(cid:146)(cid:102)(cid:112)(cid:33)OC(cid:34)(cid:129)(cid:154)(cid:36)4x3y=0(cid:37) 4 (cid:112)(cid:33)OC(cid:49)(cid:112)(cid:33)x1=0(cid:34)(cid:108)(cid:40)(cid:36)(1, )(cid:37) 3 4 4 k 7 (cid:114)(cid:41)(cid:209)(cid:40)(cid:34)(cid:112)(cid:33)(cid:36)y =k(x1)(cid:37)(cid:48) 3 (cid:37)(cid:116)(cid:85)k = (cid:37) 3 =1 24 k21 (cid:210)(cid:84)(cid:209)(cid:45)(cid:33)(cid:34)(cid:129)(cid:154)(cid:36)7x24y25=0.((cid:187)(cid:22)(cid:44)(cid:109)(cid:110)) [(cid:129)(cid:130)(cid:52)](cid:10)(cid:69)x2y2 =1(cid:34)(cid:69)(cid:70)(cid:36)O0,0(cid:37)(cid:120)(cid:121)(cid:36)1(cid:37) (cid:69)(x3)2(y4)2 =16(cid:34)(cid:69)(cid:70)O (cid:36)(3,4)(cid:37)(cid:120)(cid:121)(cid:36)4(cid:37) 1 (cid:126)(cid:69)(cid:69)(cid:70)(cid:72)(cid:36) 3242 =5 (cid:37)(cid:119)(cid:98)(cid:126)(cid:69)(cid:120)(cid:121)(cid:180)(cid:107)(cid:37)(cid:122)(cid:126)(cid:69)(cid:201)(cid:45)(cid:37) (cid:211)(cid:158)(cid:37) 4 3 3 (cid:51)(cid:45)(cid:33)(cid:36)l(cid:54)(cid:37)(cid:144)(cid:36)k = (cid:37)(cid:146)(cid:147)k = (cid:37)(cid:114)(cid:129)(cid:154)(cid:36)y= xt(t>0) OO1 3 l 4 4|t| d = =1 5 3 5 O(cid:71)l(cid:34)(cid:72)(cid:73) 9 (cid:37)(cid:116)(cid:85)t = (cid:37)(cid:146)(cid:147)l(cid:34)(cid:129)(cid:154)(cid:36)y= x (cid:37) 1 4 4 4 16 (cid:51)(cid:45)(cid:33)(cid:36)m(cid:54)(cid:37)(cid:114)(cid:112)(cid:33)(cid:129)(cid:154)(cid:36)kxy p=0(cid:37)(cid:179)(cid:106)p>0(cid:37)k <0(cid:37) ì p ï =1 ì k = 7 ï 1k2 ï ï 24 7 25 (cid:202)(cid:21)(cid:155)í (cid:37)(cid:116)(cid:85)í (cid:37)y= x ï3k4 p =4 ï p= 25 24 24 ï î 1k2 ïî 24 (cid:51)(cid:45)(cid:33)(cid:36)n(cid:54)(cid:37)(cid:208)(cid:183)(cid:45)(cid:33)(cid:129)(cid:154)(cid:36)x=1(cid:37) 3 5 7 25 (cid:122)(cid:61)(cid:62)(cid:36)(cid:10)y= x (cid:191)y= x (cid:191)x=1. 4 4 24 24 4(cid:25)(cid:26)2022(cid:27)(cid:28)(cid:29)Ⅱ(cid:30)·15(cid:31)(cid:114)(cid:40)A(2,3),B(0,a)(cid:37)(cid:150)(cid:112)(cid:33)AB(cid:3)(cid:98)y=a(cid:212)(cid:171)(cid:34)(cid:112)(cid:33)(cid:49)(cid:69)(x3)2 (y2)2 =1 (cid:56)(cid:7)(cid:53)(cid:40)(cid:37)(cid:48)a(cid:34)(cid:213)(cid:214)(cid:215)(cid:216)(cid:92) (cid:25) é1 3ù (cid:60)(cid:61)(cid:62)(cid:63) , ê ú ë3 2û (cid:60)(cid:64)(cid:65)(cid:63)(cid:217)(cid:78)(cid:79)(cid:80)(cid:40)A(cid:3)(cid:98)y=a(cid:212)(cid:171)(cid:40)A¢(cid:34)(cid:81)(cid:82)(cid:37)(cid:109)(cid:110)(cid:85)(cid:71)(cid:112)(cid:33)l(cid:34)(cid:129)(cid:154)(cid:37)(cid:67)(cid:68)(cid:69)(cid:70)(cid:71)(cid:112)(cid:33)(cid:34)(cid:72)(cid:73)(cid:218)(cid:98)(cid:119) (cid:98)(cid:120)(cid:121)(cid:85)(cid:71)(cid:153)(cid:119)(cid:135)(cid:37)(cid:116)(cid:85)(cid:109)(cid:110)(cid:77) (cid:60)(cid:117)(cid:116)(cid:63)(cid:116)(cid:10)A2,3(cid:3)(cid:98)y=a(cid:212)(cid:171)(cid:34)(cid:40)(cid:34)(cid:81)(cid:82)(cid:36)A¢2,2a3(cid:37)B0,a(cid:102)(cid:112)(cid:33)y=a(cid:38)(cid:37) a3 (cid:146)(cid:147)A¢B(cid:146)(cid:102)(cid:112)(cid:33)(cid:109)(cid:36)(cid:112)(cid:33)l(cid:37)(cid:146)(cid:147)(cid:112)(cid:33)l(cid:36)y= xa(cid:37)(cid:109)a3x2y2a=0(cid:77) 2 (cid:69)C:x32y22 =1(cid:37)(cid:69)(cid:70)C3,2(cid:37)(cid:120)(cid:121)r=1(cid:37) 3a342a (cid:186)(cid:21)(cid:155)(cid:69)(cid:70)(cid:71)(cid:112)(cid:33)l(cid:34)(cid:72)(cid:73)d = £1(cid:37) a3222 1 3 é1 3ù (cid:109)55a2 £a3222(cid:37)(cid:116)(cid:85) £a£ (cid:37)(cid:109)aÎ ê , ú (cid:77) 3 2 ë3 2û é1 3ù (cid:122)(cid:61)(cid:62)(cid:36)(cid:10) , ê ú ë3 2û 5(cid:25)(cid:26)2023(cid:27)(cid:28)(cid:29)Ⅱ(cid:30)·15(cid:31)(cid:182)(cid:183)(cid:112)(cid:33)l:xmy1=0(cid:49)eC:x12y2 =4(cid:108)(cid:98)A(cid:37)B(cid:126)(cid:40)(cid:37)(cid:189)(cid:80)(cid:55)(cid:47)“VABC 8 (cid:177)(cid:219)(cid:36) ”(cid:34)m(cid:34)(cid:22)(cid:59)(cid:214) (cid:25) 5 1 1 (cid:60)(cid:61)(cid:62)(cid:63)2(cid:26)2,2, , (cid:106)(cid:220)(cid:155)(cid:22)(cid:59)(cid:221)(cid:110)(cid:147)(cid:31) 2 2 (cid:60)(cid:64)(cid:65)(cid:63)(cid:67)(cid:68)(cid:112)(cid:33)(cid:49)(cid:69)(cid:34)(cid:192)(cid:193)(cid:3)(cid:194)(cid:37)(cid:79)(cid:80)(cid:139)(cid:86) AB (cid:37)(cid:147)(cid:222)(cid:40)C(cid:71)(cid:112)(cid:33)AB(cid:34)(cid:72)(cid:73)(cid:37)(cid:132)(cid:133)(cid:177)(cid:219)(cid:7)(cid:135)(cid:109)(cid:110)(cid:116) (cid:80)(cid:25) (cid:60)(cid:117)(cid:116)(cid:63)(cid:114)(cid:40)C(cid:71)(cid:112)(cid:33)AB(cid:34)(cid:72)(cid:73)(cid:36)d(cid:37)(cid:202)(cid:139)(cid:86)(cid:7)(cid:135)(cid:85) AB =2 4d2 (cid:37)1 8 4 5 2 5 (cid:146)(cid:147)S = ´d´2 4d2 = (cid:37)(cid:116)(cid:85)(cid:10)d = (cid:191)d = (cid:37) (cid:223)ABC 2 5 5 5 11 2 2 4 5 2 2 5 1 (cid:202)d = = (cid:37)(cid:146)(cid:147) = (cid:191) = (cid:37)(cid:116)(cid:85)(cid:10)m=±2(cid:191)m=± (cid:25) 1m2 1m2 1m2 5 1m2 5 2 1 1 (cid:122)(cid:61)(cid:62)(cid:36)(cid:10)2(cid:26)2,2, , (cid:106)(cid:220)(cid:155)(cid:22)(cid:59)(cid:221)(cid:110)(cid:147)(cid:31)(cid:25) 2 2 (cid:22)(cid:23)(cid:112)(cid:33)(cid:34)(cid:224)(cid:151)(cid:128)(cid:107)(cid:151)(cid:152) 1(cid:23)(cid:112)(cid:33)(cid:34)(cid:224)(cid:151)(cid:128) (cid:150)(cid:112)(cid:33)l(cid:49)x(cid:225)(cid:50)(cid:108)(cid:37)(cid:48)(cid:147)x(cid:225)(cid:123)(cid:129)(cid:226)(cid:36)(cid:227)(cid:228)(cid:37)(cid:229)(cid:108)(cid:40)(cid:230)(cid:54)(cid:231)(cid:232)(cid:100)(cid:112)(cid:233)(cid:49)l(cid:234)(cid:133)(cid:146)(cid:94)(cid:34)(cid:128)(cid:171)(cid:36)(cid:112)(cid:33)l(cid:34)(cid:224)(cid:151)(cid:128)(cid:37) (cid:235)(cid:236)(cid:141)a(cid:37)b(cid:37)g(cid:37)L(cid:237)(cid:178) (cid:26)1(cid:31)(cid:150)(cid:112)(cid:33)(cid:49)x(cid:225)(cid:170)(cid:115)(cid:26)(cid:191)(cid:234)(cid:133)(cid:31)(cid:37)(cid:48)(cid:224)(cid:151)(cid:128)(cid:36)0 (cid:26)2(cid:31)(cid:224)(cid:151)(cid:128)(cid:34)(cid:213)(cid:214)(cid:215)(cid:216)aÎ[0(cid:37)p) 2(cid:23)(cid:112)(cid:33)(cid:34)(cid:151)(cid:152) (cid:114)(cid:112)(cid:33)(cid:34)(cid:224)(cid:151)(cid:128)(cid:36)a(cid:37)(cid:48)a(cid:34)(cid:123)(cid:45)(cid:214)(cid:171)(cid:36)(cid:112)(cid:33)(cid:34)(cid:151)(cid:152)(cid:37)(cid:238)(cid:36)k =tana p (cid:26)1(cid:31)(cid:51)a= (cid:54)(cid:37)(cid:151)(cid:152)(cid:153)(cid:101)(cid:102)(cid:77)(cid:146)(cid:147)(cid:239)(cid:112)(cid:33)(cid:92)(cid:153)(cid:101)(cid:102)(cid:151)(cid:152)(cid:34) 2 (cid:26)2(cid:31)(cid:224)(cid:151)(cid:128)a(cid:49)(cid:151)(cid:152)k(cid:34)(cid:3)(cid:194) (cid:51)k =0(cid:54)(cid:37)(cid:112)(cid:33)(cid:170)(cid:115)(cid:98)(cid:225)(cid:191)(cid:49)(cid:225)(cid:234)(cid:133)(cid:77) (cid:51)k >0(cid:54)(cid:37)(cid:112)(cid:33)(cid:34)(cid:224)(cid:151)(cid:128)(cid:36)(cid:149)(cid:128)(cid:37)(cid:224)(cid:151)(cid:128)(cid:240)k(cid:34)(cid:241)(cid:242)(cid:84)(cid:241)(cid:242)(cid:77) (cid:51)k <0(cid:54)(cid:37)(cid:112)(cid:33)(cid:34)(cid:224)(cid:151)(cid:128)(cid:36)(cid:145)(cid:128)(cid:37)(cid:224)(cid:151)(cid:128)(cid:240)k(cid:34)(cid:241)(cid:242)(cid:84)(cid:241)(cid:242)(cid:77) 3(cid:23)(cid:41)(cid:126)(cid:40)(cid:34)(cid:112)(cid:33)(cid:151)(cid:152)(cid:7)(cid:135) y  y (cid:182)(cid:183)(cid:112)(cid:33)(cid:38)(cid:220)(cid:155)(cid:126)(cid:40)(cid:37)A(x (cid:37)y )(cid:37)B(x (cid:37)y )(cid:48)k = 2 1 1 1 2 2 x x 2 1 (cid:26)1(cid:31)(cid:112)(cid:33)(cid:34)(cid:151)(cid:152)(cid:92)(cid:124)(cid:96)(cid:34)(cid:37)(cid:49)(cid:146)(cid:213)(cid:34)(cid:40)(cid:243)(cid:3)(cid:25) (cid:26)2(cid:31)(cid:150)x = x (cid:37)(cid:48)(cid:112)(cid:33) AB (cid:34)(cid:151)(cid:152)(cid:153)(cid:101)(cid:102)(cid:37)(cid:104)(cid:54)(cid:112)(cid:33)(cid:34)(cid:224)(cid:151)(cid:128)(cid:36)90° 1 2 4(cid:23)(cid:52)(cid:40)(cid:53)(cid:33) (cid:126)(cid:112)(cid:33)AB(cid:37)AC (cid:34)(cid:151)(cid:152)(cid:50)(cid:119)→A(cid:23)B(cid:23)C (cid:52)(cid:40)(cid:53)(cid:33)(cid:77)(cid:244)(cid:41)(cid:74)(cid:37) A(cid:23)B(cid:23)C (cid:52)(cid:40)(cid:53)(cid:33)(cid:37)(cid:48)(cid:112)(cid:33)AB(cid:37)AC (cid:34)(cid:151)(cid:152)(cid:50)(cid:119)(cid:26)(cid:151)(cid:152)(cid:101)(cid:102)(cid:54)(cid:31)(cid:191)(cid:151)(cid:152)(cid:190)(cid:153)(cid:101)(cid:102)(cid:25) (cid:137)(cid:23)(cid:112)(cid:33)(cid:34)(cid:129)(cid:154) 1(cid:23)(cid:112)(cid:33)(cid:129)(cid:154)(cid:34)(cid:245)(cid:246)(cid:247)(cid:135) (cid:276)(cid:171) (cid:129)(cid:154) (cid:277)(cid:141)(cid:215)(cid:216) (cid:40)(cid:151)(cid:135) y y =kxx  (cid:153)(cid:278)(cid:46)(cid:112)(cid:98)x(cid:225)(cid:34)(cid:112)(cid:33) 1 1 (cid:151)(cid:176)(cid:135) y=kxb (cid:153)(cid:278)(cid:46)(cid:112)(cid:98)x(cid:225)(cid:34)(cid:112)(cid:33) y y xx (cid:126)(cid:40)(cid:135) 1 = 1 (cid:153)(cid:278)(cid:112)(cid:33)x=x (x ¹ x )(cid:107)(cid:112)(cid:33)y= y (y ¹ y ) y  y x x 1 1 2 1 1 2 2 1 2 1 x y (cid:176)(cid:72)(cid:135)  =1 (cid:153)(cid:278)(cid:46)(cid:112)(cid:98)(cid:81)(cid:82)(cid:225)(cid:107)(cid:41)(cid:279)(cid:40)(cid:34)(cid:112)(cid:33) a b AxByC =0 (cid:22)(cid:280)(cid:135) (cid:170)(cid:177)(cid:112)(cid:128)(cid:81)(cid:82)(cid:194)(cid:281)(cid:34)(cid:112)(cid:33)(cid:190)(cid:277)(cid:141) (A2 B2 ¹0) 2(cid:23)(cid:79)(cid:248)(cid:33)(cid:26)(cid:191)(cid:112)(cid:33)(cid:31)(cid:129)(cid:154)(cid:34)(cid:129)(cid:130) (cid:102)(cid:182)(cid:183)(cid:248)(cid:33)(cid:249)(cid:250)(cid:34)(cid:251)(cid:252)(cid:253)(cid:37)(cid:79)(cid:248)(cid:33)(cid:26)(cid:191)(cid:112)(cid:33)(cid:31)(cid:129)(cid:154)(cid:34)(cid:254)(cid:255)(cid:235)(cid:236)(cid:56)(cid:126)(cid:246)(cid:10) (cid:26)1(cid:31)(cid:112)(cid:113)(cid:130)(cid:10)(cid:256)(cid:257)(cid:258)(cid:96)(cid:248)(cid:33)(cid:129)(cid:154)(cid:34)(cid:259)(cid:260)(cid:37)(cid:88)(cid:89)(cid:112)(cid:113)(cid:189)(cid:80)(cid:129)(cid:154)(cid:37)(cid:261)(cid:211)(cid:102)(cid:112)(cid:33)(cid:106)(cid:37)(cid:150)(cid:141)(cid:112)(cid:113)(cid:130)(cid:48)(cid:262)(cid:257)(cid:71)(cid:126)(cid:59)(cid:40)(cid:37) (cid:191)(cid:263)(cid:22)(cid:40)(cid:22)(cid:151)(cid:152) (cid:26)2(cid:31)(cid:264)(cid:113)(cid:130)(cid:10)(cid:150)(cid:21)(cid:265)(cid:44)(cid:205)(cid:49)(cid:146)(cid:79)(cid:259)(cid:260)(cid:266)(cid:194)(cid:153)(cid:267)(cid:268)(cid:37)(cid:48)(cid:29)(cid:269)(cid:78)(cid:140)(cid:141)(cid:270)(cid:96)(cid:194)(cid:13)(cid:130)(cid:114)(cid:80)(cid:248)(cid:33)(cid:129)(cid:154)(cid:37)(cid:88)(cid:89)(cid:200)(cid:140)(cid:141)(cid:44) (cid:205)(cid:116)(cid:80)(cid:271)(cid:13)(cid:34)(cid:214)(cid:26)(cid:235)(cid:236)(cid:44)(cid:205)(cid:34)(cid:59)(cid:13)(cid:49)(cid:146)(cid:79)(cid:271)(cid:13)(cid:34)(cid:59)(cid:13)(cid:22)(cid:272)(cid:31) 3(cid:23)(cid:33)(cid:273)(cid:106)(cid:40)(cid:81)(cid:82)(cid:7)(cid:135) ì x x x= 1 2 ï (cid:150)(cid:40)P(cid:37)P (cid:34)(cid:81)(cid:82)(cid:64)(cid:157)(cid:36)(x (cid:37)y )(cid:37)(x (cid:37)y )(cid:57)(cid:33)(cid:273)PP (cid:34)(cid:106)(cid:40) M (cid:34)(cid:81)(cid:82)(cid:36)(x(cid:37)y)(cid:37)(cid:48) ï í 2 (cid:37)(cid:104)(cid:7)(cid:135) 1 2 1 1 2 2 1 2 ï y= y 1  y 2 ïî 2 (cid:36)(cid:33)(cid:273)PP (cid:34)(cid:106)(cid:40)(cid:81)(cid:82)(cid:7)(cid:135)(cid:25) 1 2 4(cid:23)(cid:126)(cid:112)(cid:33)(cid:34)(cid:127)(cid:128)(cid:7)(cid:135) k k (cid:150)(cid:112)(cid:33)y=k xb(cid:49)(cid:112)(cid:33)y=k xb (cid:34)(cid:127)(cid:128)(cid:36)a(cid:37)(cid:48)tana= 2 1 . 1 1 2 2 1kk 1 2 (cid:52)(cid:23)(cid:126)(cid:112)(cid:33)(cid:170)(cid:115)(cid:49)(cid:46)(cid:112)(cid:34)(cid:75)(cid:96) (cid:126)(cid:44)(cid:112)(cid:33)(cid:170)(cid:115)(cid:49)(cid:46)(cid:112)(cid:34)(cid:75)(cid:96)(cid:147)(cid:237)(cid:274)(cid:247)(cid:135)(cid:80)(cid:275)(cid:37)(cid:211)(cid:237)(cid:146)(cid:178)(cid:25) (cid:126)(cid:112)(cid:33)(cid:129)(cid:154) (cid:170)(cid:115) (cid:46)(cid:112) l :AxB yC =0 AB A B =0(cid:57) 1 1 1 1 1 2 2 1 AA BB =0 l :A xB yC =0 BC B C ¹0 1 2 1 2 2 2 2 2 1 2 2 1l :y=k xb 1 1 1 (cid:26)(cid:151)(cid:152)(cid:101)(cid:102)(cid:31) l :y=k xb k =k ,b ¹b (cid:191) k gk =1(cid:191)k(cid:49)k (cid:106)(cid:56)(cid:22)(cid:59)(cid:36)0(cid:37)(cid:282) 2 2 2 1 2 1 2 1 2 1 2 l :x=x x=x,x=x ,x ¹ x (cid:22)(cid:59)(cid:153)(cid:101)(cid:102)(cid:25) 1 1,(cid:26)(cid:151)(cid:152)(cid:153)(cid:101)(cid:102)(cid:31) 1 2 1 2 l :x=x 2 2 (cid:283)(cid:23)(cid:52)(cid:246)(cid:72)(cid:73) 1(cid:23)(cid:126)(cid:40)(cid:264)(cid:34)(cid:72)(cid:73) (cid:170)(cid:177)(cid:38)(cid:126)(cid:40)P(x,y ),P(x ,y )(cid:34)(cid:72)(cid:73)(cid:7)(cid:135)(cid:36)|PP |= (x x )2 (y  y )2 (cid:25) 1 1 1 2 2 2 1 2 1 2 1 2 (cid:284)(cid:157)(cid:285)(cid:37)(cid:279)(cid:40)O(cid:26)0(cid:37)0(cid:31)(cid:49)(cid:220)(cid:22)(cid:40)P(cid:26)x(cid:37)y(cid:31)(cid:34)(cid:72)(cid:73)|OP|= x2  y2. 2(cid:23)(cid:40)(cid:71)(cid:112)(cid:33)(cid:34)(cid:72)(cid:73) |Ax By C| (cid:40)P(x ,y )(cid:71)(cid:112)(cid:33)l:AxByC =0(cid:34)(cid:72)(cid:73)d = 0 0 0 0 0 A2 B2 (cid:284)(cid:157)(cid:285)(cid:37)(cid:150)(cid:112)(cid:33)(cid:36)l(cid:10)x=m(cid:37)(cid:48)(cid:40)P(x ,y )(cid:71)l(cid:34)(cid:72)(cid:73)d =|mx |(cid:77)(cid:150)(cid:112)(cid:33)(cid:36)l(cid:10)y=n(cid:37)(cid:48)(cid:40)P(x ,y )(cid:71)l(cid:34) 0 0 0 0 0 0 0 (cid:72)(cid:73)d =|n y | 0 3(cid:23)(cid:126)(cid:44)(cid:170)(cid:115)(cid:33)(cid:264)(cid:34)(cid:72)(cid:73) (cid:182)(cid:183)l ,l (cid:92)(cid:126)(cid:44)(cid:170)(cid:115)(cid:33)(cid:37)(cid:79)l ,l (cid:264)(cid:72)(cid:73)(cid:34)(cid:129)(cid:130)(cid:10) 1 2 1 2 (cid:26)1(cid:31)(cid:100)(cid:16)(cid:36)(cid:179)(cid:106)(cid:22)(cid:44)(cid:112)(cid:33)(cid:38)(cid:34)(cid:284)(cid:286)(cid:40)(cid:71)(cid:282)(cid:22)(cid:44)(cid:112)(cid:33)(cid:34)(cid:72)(cid:73)(cid:25) |C C | (cid:26)2(cid:31)(cid:114)l :AxByC =0,l :AxByC =0(cid:37)(cid:48)l (cid:49)l (cid:180)(cid:264)(cid:34)(cid:72)(cid:73)d = 1 2 1 1 2 2 1 2 A2 B2 (cid:4)(cid:10)(cid:126)(cid:170)(cid:115)(cid:112)(cid:33)(cid:129)(cid:154)(cid:106)(cid:37)x(cid:37)y(cid:251)(cid:177)(cid:212)(cid:287)(cid:194)(cid:13)(cid:259)(cid:50)(cid:119)(cid:25) 4(cid:23)(cid:288)(cid:67)(cid:135) (cid:288)(cid:67)(cid:135) f(x)= ax2 bxc ± a x2 b xc (cid:250)(cid:289)(cid:13)(cid:79)(cid:116)(cid:37)(cid:217)(cid:78)(cid:290)(cid:71)(cid:126)(cid:40)(cid:264)(cid:34)(cid:72)(cid:73)(cid:37)(cid:191)(cid:263)(cid:140)(cid:141)(cid:125)(cid:291)(cid:103)(cid:79) 1 1 1 2 2 2 (cid:116)(cid:25) (cid:245)(cid:23)(cid:69) 1(cid:23)(cid:69)(cid:34)(cid:283)(cid:246)(cid:129)(cid:154) (cid:26)1(cid:31)(cid:69)(cid:34)(cid:82)(cid:35)(cid:129)(cid:154)(cid:10)(xa)2 (yb)2 =r2(cid:37)(cid:69)(cid:70)(cid:81)(cid:82)(cid:36)(cid:26)a(cid:37)b(cid:31)(cid:37)(cid:120)(cid:121)(cid:36)r(r >0) æ D Eö (cid:26)2(cid:31)(cid:69)(cid:34)(cid:22)(cid:280)(cid:129)(cid:154)(cid:10)x2  y2 DxEyF =0(D2 E2 4F >0)(cid:37)(cid:69)(cid:70)(cid:81)(cid:82)(cid:36) ç , ÷ (cid:37)(cid:120)(cid:121) è 2 2ø D2 E2 4F r = 2 (cid:26)3(cid:31)(cid:69)(cid:34)(cid:112)(cid:121)(cid:135)(cid:129)(cid:154)(cid:10)(cid:150)A(x,y ),B(x ,y )(cid:37)(cid:48)(cid:147)(cid:33)(cid:273)AB(cid:36)(cid:112)(cid:121)(cid:34)(cid:69)(cid:34)(cid:129)(cid:154)(cid:92) 1 1 2 2 (xx )(xx )(y y )(y y )=0 1 2 1 2 2(cid:23)(cid:40)(cid:49)(cid:69)(cid:34)(cid:192)(cid:193)(cid:3)(cid:194)(cid:75)(cid:76)(cid:26)1(cid:31)(cid:40)P(x ,y )(cid:49)(cid:69)(xa)2 (yb)2 =r2(cid:34)(cid:192)(cid:193)(cid:3)(cid:194)(cid:10) 0 0 (xa)2 (yb)2 >r2 Û(cid:40)P(cid:102)(cid:69)(cid:201)(cid:77) ①(xa)2 (yb)2 =r2 Û(cid:40)P(cid:102)(cid:69)(cid:38)(cid:77) ②(xa)2 (yb)2 0Û(cid:40)P(cid:102)(cid:69)(cid:201)(cid:77) 0 0 0 0 ①x2  y2 Dx Ey F =0Û(cid:40)P(cid:102)(cid:69)(cid:38)(cid:77) 0 0 0 0 ②x2  y2 Dx Ey F <0Û(cid:40)P(cid:102)(cid:69)(cid:281)(cid:25) 0 0 0 0 ③(cid:292)(cid:23)(cid:112)(cid:33)(cid:49)(cid:69)(cid:34)(cid:192)(cid:193)(cid:3)(cid:194) 1(cid:23)(cid:112)(cid:33)(cid:49)(cid:69)(cid:34)(cid:192)(cid:193)(cid:3)(cid:194)(cid:75)(cid:76) (cid:26)1(cid:31)(cid:293)(cid:294)(cid:130)(cid:26)(cid:69)(cid:70)(cid:71)(cid:112)(cid:33)(cid:34)(cid:72)(cid:73)(cid:107)(cid:120)(cid:121)(cid:3)(cid:194)(cid:31) (cid:69)(cid:70)(a,b)(cid:71)(cid:112)(cid:33)AxByC =0(cid:34)(cid:72)(cid:73)(cid:37)(cid:48) d = |AaBbC|(cid:10) A2 B2 drÛ(cid:112)(cid:33)(cid:49)(cid:69)(cid:50)(cid:73) (cid:26)2(cid:31)(cid:161)(cid:13)(cid:129)(cid:130)(cid:26)(cid:293)(cid:294)(cid:99)(cid:21)(cid:100)(cid:16)(cid:36)(cid:161)(cid:13)(cid:99)(cid:21)(cid:109)(cid:108)(cid:40)(cid:59)(cid:13)(cid:99)(cid:21)(cid:100)(cid:16)(cid:36)(cid:129)(cid:154)(cid:67)(cid:59)(cid:13)(cid:31) ì AxByC=0 (cid:202)í (cid:37) î(xa)2(yb)2 =r2 (cid:295)(cid:296)(cid:85)(cid:71)(cid:22)(cid:296)(cid:137)(cid:297)(cid:129)(cid:154) px2  qx  t = 0 (cid:37) px2  qx  t = 0 (cid:75)(cid:157)(cid:135)(cid:36)D (cid:37)(cid:48)(cid:10) D>0Û(cid:112)(cid:33)(cid:49)(cid:69)(cid:50)(cid:108)(cid:77) D=0Û(cid:112)(cid:33)(cid:49)(cid:69)(cid:50)(cid:45)(cid:77) D<0Û(cid:112)(cid:33)(cid:49)(cid:69)(cid:50)(cid:73)(cid:25) (cid:298)(cid:23)(cid:126)(cid:69)(cid:192)(cid:193)(cid:3)(cid:194)(cid:34)(cid:75)(cid:76) (cid:141)(cid:126)(cid:69)(cid:34)(cid:69)(cid:70)(cid:72)(cid:49)(cid:126)(cid:69)(cid:120)(cid:121)(cid:34)(cid:107)(cid:184)(cid:242)(cid:218)(cid:3)(cid:194)(cid:124)(cid:96)(cid:37)(cid:299)(cid:300)(cid:92)(cid:10) (cid:114)(cid:126)(cid:69) O ,O (cid:34)(cid:120)(cid:121)(cid:64)(cid:157)(cid:92)R,r (cid:37)(cid:26)(cid:153)(cid:199)(cid:114)R>r(cid:31)(cid:37)(cid:57)(cid:126)(cid:69)(cid:34)(cid:69)(cid:70)(cid:72)(cid:36)d(cid:37)(cid:48)(cid:10) 1 2 d r(cid:37)(cid:69)(cid:70)(cid:72)(cid:36)d(cid:37)(cid:48)(cid:126)(cid:69)(cid:34)(cid:192)(cid:193)(cid:3)(cid:194)(cid:110)(cid:141)(cid:253)(cid:237)(cid:74)(cid:237)(cid:178)(cid:10) (cid:192)(cid:193)(cid:3)(cid:194) (cid:50)(cid:73) (cid:201)(cid:45) (cid:50)(cid:108) (cid:281)(cid:45) (cid:281)(cid:278) (cid:293)(cid:294)(cid:284)(cid:302) d >Rr d =Rr Rr0)(cid:34)(cid:271)(cid:13)(cid:129)(cid:154)(cid:36)í (cid:26)q(cid:36)(cid:271)(cid:13)(cid:31)(cid:77) îy=rsinq ① ìx=arcosq (xa)2 (yb)2 =r2(r >0)(cid:34)(cid:271)(cid:13)(cid:129)(cid:154)(cid:36)í (cid:26)q(cid:36)(cid:271)(cid:13)(cid:31)(cid:25) îy=brsinq ② (cid:4)(cid:155)(cid:10)(cid:212)(cid:98)(cid:69)(cid:34)(cid:314)(cid:214)(cid:99)(cid:21)(cid:37)(cid:315)(cid:315)(cid:110)(cid:147)(cid:140)(cid:141)(cid:69)(cid:34)(cid:271)(cid:13)(cid:129)(cid:154)(cid:316)(cid:39)(cid:40)(cid:34)(cid:81)(cid:82)(cid:114)(cid:36)(arcosq,brsinq)(cid:26)q(cid:36)(cid:271)(cid:13)(cid:37) (cid:26)a,b(cid:31)(cid:36)(cid:69)(cid:70)(cid:37)r(cid:36)(cid:120)(cid:121)(cid:31)(cid:37)(cid:147)(cid:207)(cid:317)(cid:318)(cid:319)(cid:34)(cid:59)(cid:13)(cid:37)(cid:162)(cid:95)(cid:52)(cid:128)(cid:289)(cid:13)(cid:135)(cid:37)(cid:210)(cid:84)(cid:320)(cid:161)(cid:13)(cid:99)(cid:21)(cid:100)(cid:16)(cid:36)(cid:52)(cid:128)(cid:99)(cid:21)(cid:37)(cid:88)(cid:89) (cid:140)(cid:141)(cid:123)(cid:139)(cid:250)(cid:191)(cid:138)(cid:139)(cid:250)(cid:289)(cid:13)(cid:34)(cid:56)(cid:321)(cid:103)(cid:79)(cid:116)(cid:314)(cid:214)(cid:25) 2(cid:23)(cid:3)(cid:98)(cid:69)(cid:34)(cid:45)(cid:33)(cid:34)(cid:293)(cid:59)(cid:234)(cid:259)(cid:132)(cid:198) (cid:26)1(cid:31)(cid:41)(cid:69) x2  y2 =r2(cid:38)(cid:22)(cid:40) P(x ,y ) (cid:34)(cid:69)(cid:34)(cid:45)(cid:33)(cid:129)(cid:154)(cid:36) x x  y y = r2(cid:25) 0 0 0 0 (cid:26)2(cid:31)(cid:41)(cid:69) (x  a)2  (y b)2 = r2(cid:38)(cid:22)(cid:40) P(x ,y ) (cid:34)(cid:69)(cid:34)(cid:45)(cid:33)(cid:129)(cid:154)(cid:36) 0 0 (x a)(xa)(y b)(y b)= r2 0 0 (cid:26)3(cid:31)(cid:41)(cid:69) x2  y2  Dx  Ey  F = 0 (cid:38)(cid:22)(cid:40) P(x ,y ) (cid:34)(cid:69)(cid:34)(cid:45)(cid:33)(cid:129)(cid:154)(cid:36) 0 0 xx y y x x y yD× 0 E× 0 F =0 0 0 2 2 (cid:26)4(cid:31)(cid:79)(cid:41)(cid:69) x2  y2 =r2(cid:201)(cid:22)(cid:40) P(x ,y ) (cid:34)(cid:69)(cid:34)(cid:45)(cid:33)(cid:129)(cid:154)(cid:54)(cid:37)(cid:287)(cid:4)(cid:155)(cid:15)(cid:116)(cid:10) 0 0 (cid:146)(cid:79)(cid:45)(cid:33)(cid:22)(cid:96)(cid:56)(cid:126)(cid:44)(cid:77) ①(cid:114)(cid:112)(cid:33)(cid:129)(cid:154)(cid:180)(cid:251)(cid:37)(cid:287)(cid:212)(cid:146)(cid:79)(cid:112)(cid:33)(cid:34)(cid:151)(cid:152)(cid:92)(cid:93)(cid:101)(cid:102)(cid:322)(cid:147)(cid:197)(cid:198)(cid:25)(cid:114)(cid:45)(cid:33)(cid:129)(cid:154)(cid:36) y  y = k(x x ) (cid:37)(cid:140)(cid:141)(cid:69)(cid:70)(cid:71) 0 0 ②(cid:45)(cid:33)(cid:34)(cid:72)(cid:73)(cid:119)(cid:98)(cid:120)(cid:121)(cid:37)(cid:185)(cid:80)(cid:3)(cid:98)k(cid:34)(cid:129)(cid:154)(cid:37)(cid:79)(cid:80)k(cid:214)(cid:25)(cid:150)(cid:79)(cid:80)(cid:34)k(cid:214)(cid:56)(cid:126)(cid:59)(cid:37)(cid:48)(cid:323)(cid:324)(cid:151)(cid:152)(cid:153)(cid:101)(cid:102)(cid:34)(cid:195)(cid:247)(cid:153)(cid:204) (cid:133)(cid:21)(cid:155)(cid:77)(cid:150)(cid:79)(cid:80)(cid:34)k(cid:214)(cid:325)(cid:56)(cid:22)(cid:59)(cid:37)(cid:48)(cid:323)(cid:324)(cid:151)(cid:152)(cid:153)(cid:101)(cid:102)(cid:34)(cid:195)(cid:247)(cid:204)(cid:133)(cid:21)(cid:155)(cid:25) (cid:22)(cid:23)(cid:125)(cid:20)(cid:21) 1(cid:25)(cid:26)2024·(cid:326)(cid:327)(cid:27)(cid:138)·(cid:137)(cid:328)(cid:31)(cid:182)(cid:183)(cid:112)(cid:33)xay=0(cid:108)(cid:69)C(cid:10)x2y22 3x2y=0(cid:98)M(cid:37)N(cid:126)(cid:40)(cid:37)(cid:48)“(cid:223)MCN (cid:36)(cid:123)(cid:52)(cid:128)(cid:247)”(cid:92)“a=0”(cid:34)(cid:26) (cid:31) A(cid:25)(cid:329)(cid:64)(cid:153)(cid:330)(cid:259)(cid:44)(cid:205) B(cid:25)(cid:330)(cid:259)(cid:153)(cid:329)(cid:64)(cid:44)(cid:205) C(cid:25)(cid:329)(cid:259)(cid:44)(cid:205) D(cid:25)(cid:331)(cid:153)(cid:329)(cid:64)(cid:332)(cid:153)(cid:330)(cid:259)(cid:44)(cid:205) (cid:60)(cid:61)(cid:62)(cid:63)B (cid:60)(cid:64)(cid:65)(cid:63)(cid:79)(cid:80)(cid:69)(cid:34)(cid:69)(cid:70)(cid:222)(cid:120)(cid:121)(cid:89)(cid:37)(cid:132)(cid:133)(cid:123)(cid:52)(cid:128)(cid:247)(cid:34)(cid:103)(cid:131)(cid:110)(cid:333)(cid:87)(cid:80)(cid:51)(cid:223)MCN(cid:36)(cid:123)(cid:52)(cid:128)(cid:247)(cid:54)a(cid:34)(cid:214)(cid:37)(cid:132)(cid:133)(cid:329)(cid:64) (cid:44)(cid:205)(cid:49)(cid:330)(cid:259)(cid:44)(cid:205)(cid:96)(cid:97)(cid:109)(cid:110)(cid:75)(cid:76).   (cid:60)(cid:117)(cid:116)(cid:63)(cid:202)C(cid:10)x2y22 3x2y=0(cid:110)(cid:85)(cid:179)(cid:69)(cid:70)(cid:36)C 3,1 (cid:37)(cid:120)(cid:121)r=2(cid:37) 3a (cid:69)(cid:70)(cid:71)(cid:112)(cid:33)xay=0(cid:34)(cid:72)(cid:73)d = (cid:37) 1a2 3 3a (cid:150)(cid:223)MCN(cid:36)(cid:123)(cid:52)(cid:128)(cid:247)(cid:37)(cid:48)(cid:56)d= r(cid:37)(cid:109) = 3(cid:37) 2 1a2 (cid:109)a2 3a=0(cid:37)(cid:116)(cid:85)a=0(cid:191)a= 3(cid:37) (cid:122)“(cid:223)MCN(cid:36)(cid:123)(cid:52)(cid:128)(cid:247)”(cid:92)“a=0”(cid:34)(cid:330)(cid:259)(cid:153)(cid:329)(cid:64)(cid:44)(cid:205). (cid:122)(cid:20)(cid:10)B. 2(cid:25)(cid:26)2024·(cid:334)(cid:327)(cid:327)(cid:335)·(cid:52)(cid:328)(cid:31)(cid:150)(cid:41)(cid:40)P0,1(cid:110)(cid:42)(cid:69)x2y22x4ya=0(cid:34)(cid:126)(cid:44)(cid:45)(cid:33)(cid:37)(cid:48)a(cid:34)(cid:213)(cid:214)(cid:215)(cid:216)(cid:92)(cid:26) (cid:31) A(cid:25)3,¥ B(cid:25)1,3 C(cid:25)3,5 D(cid:25)5,¥ (cid:60)(cid:61)(cid:62)(cid:63)C (cid:60)(cid:64)(cid:65)(cid:63)(cid:67)(cid:68)(cid:40)(cid:102)(cid:69)(cid:201)(cid:109)(cid:110)(cid:79)(cid:116). (cid:60)(cid:117)(cid:116)(cid:63)(cid:69)x2y22x4ya=0(cid:37)(cid:109)(cid:69)x12y22 =5a(cid:37)(cid:48)5a>0(cid:37)(cid:116)(cid:85)a<5(cid:25) (cid:41)(cid:40)P0,1(cid:56)(cid:126)(cid:44)(cid:45)(cid:33)(cid:37)(cid:48)(cid:40)P(cid:102)(cid:69)(cid:201)(cid:37) 102212 > 5a (cid:37)(cid:109)2>5a(cid:37)(cid:116)(cid:85)a>3(cid:25) (cid:122)31(cid:37)(cid:110)(cid:183)(cid:112)(cid:33)l(cid:49)(cid:69)O(cid:50)(cid:73)(cid:37) 2 OA 1 (cid:144)(cid:36)ÐAPB=2ÐAPO(cid:37)(cid:57)sinÐAPO= = (cid:37) OP OP(cid:51)OP (cid:314)(cid:218)(cid:54)(cid:37)(cid:48)sinÐAPO(cid:314)(cid:242)(cid:37)(cid:110)(cid:85)ÐAPO(cid:314)(cid:242)(cid:37)(cid:109)ÐAPB(cid:314)(cid:242)(cid:37) (cid:206)(cid:144)(cid:36)OP (cid:34)(cid:314)(cid:218)(cid:214)(cid:109)(cid:36)(cid:69)(cid:70)O(cid:71)(cid:112)(cid:33)l(cid:34)(cid:72)(cid:73)(cid:36) 2(cid:37) 2 π π (cid:104)(cid:54)sinÐAPO= ,ÐAPO= (cid:37)(cid:146)(cid:147)ÐAPB(cid:213)(cid:85)(cid:314)(cid:242)(cid:214) (cid:25) 2 4 2 (cid:122)(cid:20)(cid:10)C(cid:25) 6(cid:25)(cid:26)2024·(cid:234)(cid:346)·(cid:137)(cid:328)(cid:31)(cid:182)(cid:183)(cid:69)O:x2y2 =3,P(cid:92)(cid:69)O(cid:201)(cid:22)(cid:40)(cid:37)(cid:41)(cid:40)P(cid:42)(cid:69)O(cid:34)(cid:126)(cid:44)(cid:45)(cid:33)(cid:37)(cid:45)(cid:40)(cid:64)(cid:157)(cid:36)A,B(cid:37) uuur uuur 9 (cid:150)PA×PB= (cid:37)(cid:48)OP =(cid:26) (cid:31) 2 A(cid:25) 6 B(cid:25)3 C(cid:25)2 3 D(cid:25) 15 (cid:60)(cid:61)(cid:62)(cid:63)C 6 (cid:60)(cid:64)(cid:65)(cid:63)(cid:114)ÐAPO=ÐBPO=a,OP =x(x> 3)(cid:37)(cid:110)(cid:85)cosÐAPB=1 (cid:37)(cid:83)(cid:84)(cid:110)(cid:85) x2 u P u A ur × u P u B ur =| u P u A ur |2 cosÐAPB= 9 Þ  x23 æ ç1 6 ö ÷= 9 (cid:37)(cid:79)(cid:116)(cid:109)(cid:110). 2 è x2 ø 2 (cid:60)(cid:117)(cid:116)(cid:63)(cid:202)x2y2 =3(cid:37)(cid:110)(cid:85)(cid:69)(cid:70)O(0,0)(cid:37)(cid:120)(cid:121)r= 3(cid:37) (cid:114)ÐAPO=ÐBPO=a,OP =x(x> 3)(cid:37) 3 x23 uuur uuur (cid:48)sina= ,cosa= , PA = PB = x23(cid:37) x x 6 cosÐAPB=cos2a=12sin2a=1 (cid:37) x2 (cid:48)(cid:56) u P u A ur × u P u B ur =| u P u A ur |2 cosÐAPB= 9 Þ  x23 æ ç1 6 ö ÷= 9 2 è x2 ø 2 Þ2x427x236=0(cid:37) (cid:116)(cid:85)  2x23  x212  =0,Qx2 >3,\x2 =12(cid:37)(cid:109)x=2 3.(cid:122)(cid:20)(cid:10)C. 7(cid:25)(cid:26)2024·(cid:336)(cid:337)·(cid:52)(cid:328)(cid:31)(cid:182)(cid:183)(cid:69)C:  x 3 2 y12 =1(cid:107)(cid:126)(cid:40)At,0,Bt,0t>0(cid:37)(cid:150)(cid:69)C(cid:38)(cid:101)(cid:102)(cid:40)P(cid:37) uuur uuur (cid:347)(cid:85)PA×PB=0(cid:37)(cid:48)t(cid:34)(cid:213)(cid:214)(cid:215)(cid:216)(cid:36)(cid:26) (cid:31) A(cid:25)0,1  B(cid:25) 1,3  C(cid:25)2,3 D(cid:25) 3,4  (cid:60)(cid:61)(cid:62)(cid:63)B uuur uuur (cid:60)(cid:64)(cid:65)(cid:63)(cid:202)PA×PB=0(cid:183)(cid:40)P(cid:34)(cid:338)(cid:339)(cid:129)(cid:154)(cid:92)(cid:147)AB(cid:192)(cid:112)(cid:121)(cid:34)(cid:69)(cid:37)(cid:110)(cid:85) t1 £ OC £t1(cid:37)(cid:109)(cid:110)(cid:79)(cid:80)t(cid:34)(cid:213)(cid:214)(cid:215) (cid:216). uuur uuur (cid:60)(cid:117)(cid:116)(cid:63)PA×PB=0(cid:323)(cid:324)P(cid:102)(cid:147)AB(cid:36)(cid:112)(cid:121)(cid:34)(cid:69)x2y2 =t2(cid:38)(cid:37) (cid:84)P(cid:206)(cid:102)(cid:69)C(cid:38)(cid:37)(cid:144)(cid:104)(cid:126)(cid:69)(cid:56)(cid:7)(cid:53)(cid:40)(cid:37) (cid:48)(cid:69)(cid:70)(cid:72)(cid:192)(cid:98)(cid:120)(cid:121)(cid:184)(cid:34)(cid:348)(cid:212)(cid:214)(cid:49)(cid:120)(cid:121)(cid:107)(cid:34)(cid:349)(cid:350)(cid:264)(cid:106)(cid:37) (cid:146)(cid:147) t1 £ OC £t1(cid:37)(cid:109) t1 £2£t1(cid:37)(cid:206)t>0(cid:37)(cid:116)(cid:85)1£t £3. (cid:122)(cid:20)(cid:10)B 8(cid:25)(cid:26)2024·(cid:351)(cid:352)(cid:353)(cid:354)·(cid:52)(cid:328)(cid:31)(cid:150)(cid:69)x2y2ax 3y2a3=0(cid:49)x(cid:225)(cid:355)(cid:56)(cid:108)(cid:40)(cid:37)(cid:48)(cid:303)(cid:13)a(cid:34)(cid:213)(cid:214)(cid:215)(cid:216)(cid:36)(cid:26) (cid:31) A(cid:25)2,6 B(cid:25)3,5 C(cid:25)2,3 U 5,6 D(cid:25)2,3 U 6,¥ (cid:60)(cid:61)(cid:62)(cid:63)C (cid:60)(cid:64)(cid:65)(cid:63)(cid:79)(cid:80)(cid:69)(cid:70)(cid:81)(cid:82)(cid:140)(cid:141)(cid:293)(cid:294)(cid:130)(cid:85)(cid:71)(cid:153)(cid:119)(cid:135)(cid:37)(cid:116)(cid:80)(cid:109)(cid:110). æ aö 2 æ 3ö 2 1 15 (cid:60)(cid:117)(cid:116)(cid:63)x2y2ax 3y2a3=0(cid:109) çx ÷ ç ç y ÷ ÷ = a22a (cid:37) è 2ø è 2 ø 4 4 1 15 a22a >0(cid:37)(cid:116)(cid:85)a<3(cid:191)a>5(cid:37) 4 4 æ a 3ö (cid:57)(cid:179)(cid:69)(cid:70)(cid:81)(cid:82)(cid:36)ç , ÷(cid:37)(cid:150)(cid:209)(cid:69)(cid:49)x(cid:225)(cid:355)(cid:56)(cid:108)(cid:40)(cid:37) ç ÷ è 2 2 ø (cid:48) 3 > 1 a22a 15 (cid:37)(cid:116)(cid:85)aÎ2,3 U 5,6 2 4 4 (cid:122)(cid:20)(cid:10)C. 9(cid:25)(cid:26)2024·(cid:336)(cid:337)·(cid:52)(cid:328)(cid:31)(cid:182)(cid:183)(cid:112)(cid:33)l:axa1y2=0(cid:37)(cid:69)O:x2y2 =16(cid:37)(cid:253)(cid:185)(cid:323)(cid:130)(cid:356)(cid:357)(cid:34)(cid:92)(cid:26) (cid:31)A(cid:25)(cid:212)(cid:220)(cid:155)(cid:303)(cid:13)a(cid:37)(cid:112)(cid:33)l(cid:49)(cid:69)O(cid:56)(cid:126)(cid:59)(cid:153)(cid:301)(cid:34)(cid:7)(cid:53)(cid:40)(cid:77) 1 B(cid:25)(cid:51)(cid:57)(cid:58)(cid:51)a= (cid:54)(cid:37)(cid:112)(cid:33)l(cid:358)(cid:69)O(cid:146)(cid:176)(cid:139)(cid:86)(cid:36)4 2(cid:77) 2 C(cid:25)(cid:212)(cid:220)(cid:155)(cid:303)(cid:13)a(cid:37)(cid:69)O(cid:153)(cid:3)(cid:98)(cid:112)(cid:33)l(cid:212)(cid:171)(cid:77) D(cid:25)(cid:101)(cid:102)(cid:303)(cid:13)a(cid:37)(cid:347)(cid:85)(cid:112)(cid:33)l(cid:49)(cid:69)O(cid:50)(cid:45)(cid:25) (cid:60)(cid:61)(cid:62)(cid:63)D (cid:60)(cid:64)(cid:65)(cid:63)(cid:79)(cid:80)(cid:112)(cid:33)l(cid:146)(cid:41)(cid:34)(cid:96)(cid:40)(cid:37)(cid:359)(cid:75)(cid:76)(cid:209)(cid:96)(cid:40)(cid:49)(cid:69)O(cid:34)(cid:192)(cid:193)(cid:3)(cid:194)(cid:37)(cid:200)(cid:360)(cid:66)(cid:64)(cid:65)(cid:75)(cid:76)(cid:109)(cid:110)(cid:85)(cid:116). ìxy=0 ìx=2 (cid:60)(cid:117)(cid:116)(cid:63)(cid:112)(cid:33)l:a(xy)y2=0(cid:37)(cid:202)í (cid:37)(cid:116)(cid:85)í (cid:37)(cid:109)(cid:112)(cid:33)l(cid:361)(cid:41)(cid:96)(cid:40)A(2,2)(cid:37) îy2=0 îy=2 (cid:69)O(cid:34)(cid:120)(cid:121)r=4(cid:37)|OA|= 22(2)2 =2 2<4(cid:37)(cid:109)(cid:40)A(2,2)(cid:102)(cid:69)O(cid:281)(cid:37) (cid:212)(cid:220)(cid:155)(cid:303)(cid:13)a(cid:37)(cid:112)(cid:33)l(cid:49)(cid:69)O(cid:56)(cid:126)(cid:59)(cid:153)(cid:301)(cid:34)(cid:7)(cid:53)(cid:40)(cid:37)A(cid:123)(cid:124)(cid:37)D(cid:356)(cid:357)(cid:77) (cid:112)(cid:33)l(cid:153)(cid:41)(cid:69)O(cid:34)(cid:69)(cid:70)(cid:37)(cid:144)(cid:104)(cid:212)(cid:220)(cid:155)(cid:303)(cid:13)a(cid:37)(cid:69)O(cid:153)(cid:3)(cid:98)(cid:112)(cid:33)l(cid:212)(cid:171)(cid:37)C(cid:123)(cid:124)(cid:77) 1 a (cid:112)(cid:33)OA(cid:34)(cid:151)(cid:152)k =1(cid:37)(cid:51)a= (cid:54)(cid:37)(cid:112)(cid:33)l(cid:34)(cid:151)(cid:152)(cid:36) =1(cid:37)(cid:144)(cid:104)(cid:112)(cid:33)l ^OA 2 a1 (cid:104)(cid:54)(cid:112)(cid:33)l(cid:358)(cid:69)O(cid:146)(cid:176)(cid:139)(cid:92)(cid:41)(cid:40)A(cid:34)(cid:314)(cid:362)(cid:139)(cid:37)(cid:314)(cid:362)(cid:139)(cid:86)(cid:36)2 r2|OA|2 =4 2(cid:37) 1 (cid:144)(cid:104)(cid:51)(cid:57)(cid:58)(cid:51)a= (cid:54)(cid:37)(cid:112)(cid:33)l(cid:358)(cid:69)O(cid:146)(cid:176)(cid:139)(cid:86)(cid:36)4 2(cid:37)B(cid:123)(cid:124). 2 (cid:122)(cid:20)(cid:10)D 10(cid:25)(cid:26)2024·(cid:326)(cid:327)(cid:363)(cid:364)·(cid:52)(cid:328)(cid:31)(cid:182)(cid:183)mÎR(cid:37)(cid:112)(cid:33)l :mxy2m=0(cid:49)l :xmy4m=0(cid:34)(cid:108)(cid:40)P(cid:102)(cid:69)C(cid:10) 1 2 x32y42 =r2r>0(cid:38)(cid:37)(cid:48)r(cid:34)(cid:314)(cid:242)(cid:214)(cid:92)(cid:26) (cid:31) A(cid:25)4 2 B(cid:25) 3 2 C(cid:25)2 5 D(cid:25)3 5 (cid:60)(cid:61)(cid:62)(cid:63)D (cid:60)(cid:64)(cid:65)(cid:63)(cid:67)(cid:68)(cid:126)(cid:112)(cid:33)(cid:129)(cid:154)(cid:110)(cid:183)(cid:126)(cid:112)(cid:33)(cid:64)(cid:157)(cid:41)(cid:96)(cid:40)(cid:57)(cid:46)(cid:112)(cid:37)(cid:110)(cid:79)(cid:85)P(cid:40)(cid:338)(cid:339)(cid:129)(cid:154)(cid:37)(cid:200)(cid:202)(cid:69)(cid:49)(cid:69)(cid:34)(cid:192)(cid:193)(cid:3)(cid:194)(cid:257) (cid:80)(cid:69)(cid:70)(cid:72)(cid:49)(cid:126)(cid:69)(cid:120)(cid:121)(cid:180)(cid:264)(cid:34)(cid:3)(cid:194)(cid:110)(cid:85)(cid:132)(cid:365). (cid:60)(cid:117)(cid:116)(cid:63)(cid:208)(cid:183)(cid:112)(cid:33)l :mxy2m=0(cid:361)(cid:41)(cid:96)(cid:40)A2,0(cid:37) 1 (cid:112)(cid:33)l :xmy4m=0(cid:361)(cid:41)(cid:96)(cid:40)B0,4(cid:37) 2 (cid:57)m´11´m=0(cid:37)(cid:208)(cid:183)(cid:112)(cid:33)l (cid:49)l (cid:366)(cid:50)(cid:46)(cid:112)(cid:37)(cid:109)(cid:110)(cid:85)ÐAPB=90o(cid:37) 1 2 (cid:146)(cid:147)P(cid:40)(cid:338)(cid:339)(cid:92)(cid:147)AB(cid:36)(cid:112)(cid:121)(cid:34)(cid:69)(cid:37)(cid:69)(cid:70)(cid:36)AB(cid:34)(cid:106)(cid:40)1,2(cid:37)(cid:120)(cid:121)(cid:36) 5(cid:77)(cid:110)(cid:85)P(cid:40)(cid:338)(cid:339)(cid:129)(cid:154)(cid:36)x12y22 =5(cid:77) (cid:206)(cid:144)(cid:36)P(cid:40)(cid:102)(cid:69)C(cid:38)(cid:37)(cid:146)(cid:147)(cid:110)(cid:85)(cid:69)x12y22 =5(cid:49)(cid:69)C(cid:56)(cid:7)(cid:53)(cid:40)(cid:37) (cid:51)(cid:126)(cid:69)(cid:281)(cid:45)(cid:26)(cid:69)C(cid:102)(cid:201)(cid:31)(cid:54)(cid:37)r(cid:213)(cid:85)(cid:314)(cid:242)(cid:214)(cid:77) (cid:104)(cid:54)(cid:55)(cid:47) 312422 =r 5(cid:37)(cid:116)(cid:85)r=3 5. (cid:122)(cid:20)(cid:10)D (cid:137)(cid:23)(cid:24)(cid:20)(cid:21) 11(cid:25)(cid:26)2024·(cid:342)(cid:343)(cid:86)(cid:367)·(cid:52)(cid:328)(cid:31)(cid:182)(cid:183)(cid:69) C:x22y2 =4(cid:37)(cid:112)(cid:33) l:m1x2y1m=0mÎR (cid:37)(cid:48)(cid:26) (cid:31) A(cid:25)(cid:112)(cid:33) l (cid:361)(cid:41)(cid:96)(cid:40) 1,1 B(cid:25)(cid:51)m=0(cid:54)(cid:37)(cid:69)C(cid:38)(cid:368)(cid:56)(cid:52)(cid:59)(cid:40)(cid:71)(cid:112)(cid:33)l(cid:34)(cid:72)(cid:73)(cid:119)(cid:98) 1 C(cid:25)(cid:112)(cid:33)l(cid:49)(cid:69)C(cid:110)(cid:369)(cid:50)(cid:45) D(cid:25)(cid:150)(cid:69)C(cid:49)(cid:69) x2y22x8ya=0(cid:368)(cid:56)(cid:52)(cid:44)(cid:7)(cid:45)(cid:33)(cid:37)(cid:48)a= 8 (cid:60)(cid:61)(cid:62)(cid:63)AD (cid:60)(cid:64)(cid:65)(cid:63)(cid:305)(cid:21)(cid:78)(cid:67)(cid:68)(cid:112)(cid:33)l(cid:34)(cid:129)(cid:154)(cid:75)(cid:76)(cid:80)(cid:112)(cid:33)l(cid:361)(cid:41)(cid:34)(cid:96)(cid:40)(cid:37)(cid:200)(cid:75)(cid:76)(cid:209)(cid:96)(cid:40)(cid:49)(cid:69)(cid:34)(cid:192)(cid:193)(cid:3)(cid:194)(cid:37)(cid:110)(cid:116)(cid:258)(cid:20)(cid:66)A (cid:107)(cid:20)(cid:66)C(cid:34)(cid:99)(cid:21)(cid:77)(cid:67)(cid:68)(cid:69)(cid:70)(cid:71)(cid:112)(cid:33)lm=0(cid:34)(cid:72)(cid:73)(cid:75)(cid:76)(cid:55)(cid:47)(cid:44)(cid:205)(cid:40)(cid:34)(cid:59)(cid:13)(cid:37)(cid:110)(cid:116)(cid:258)(cid:20)(cid:66)B(cid:34)(cid:99)(cid:21)(cid:77)(cid:202)(cid:20)(cid:66)D (cid:34)(cid:44)(cid:205)(cid:110)(cid:85)(cid:126)(cid:69)(cid:201)(cid:45)(cid:37)(cid:202)(cid:104)(cid:110)(cid:79)(cid:85)(cid:271)(cid:13)a(cid:34)(cid:214). (cid:60)(cid:117)(cid:116)(cid:63)(cid:202)(cid:112)(cid:33)l:m1x2y1m=0mÎR (cid:37)(cid:85) mx1x2y1=0(cid:37) ì x1=0 ìx=1 (cid:144)(cid:36)mÎR(cid:37)(cid:48)(cid:55)(cid:47) í (cid:37)(cid:116)(cid:85) í (cid:37) îx2y1=0 îy=1 (cid:146)(cid:147)(cid:112)(cid:33)(cid:361)(cid:41)(cid:96)(cid:40) 1,1(cid:37)(cid:122)(cid:20)(cid:66)A(cid:123)(cid:124). (cid:144)(cid:36)(cid:51)m=0(cid:54)(cid:37)(cid:112)(cid:33)l(cid:36):x2y1=0(cid:37) 201 3 5 (cid:48)(cid:69)(cid:70) C2,0 (cid:71)(cid:112)(cid:33)l(cid:34)(cid:72)(cid:73)(cid:36) d = = (cid:37) 1222 5 3 5 (cid:48)(cid:104)(cid:54)(cid:112)(cid:33)l(cid:49)(cid:69)(cid:50)(cid:108)(cid:146)(cid:85)(cid:370)(cid:371)(cid:34)(cid:175)(cid:40)(cid:71)(cid:112)(cid:33)l(cid:34)(cid:72)(cid:73)d =2 Î(0,1)(cid:37) 1 5 (cid:146)(cid:147)(cid:69)(cid:38)(cid:325)(cid:56) 2 (cid:59)(cid:40)(cid:71)(cid:112)(cid:33)(cid:34)(cid:72)(cid:73)(cid:36) 1(cid:37)(cid:122)(cid:20)(cid:66)B(cid:356)(cid:357). (cid:144)(cid:36)(cid:112)(cid:33)l(cid:41)(cid:96)(cid:40) 1,1(cid:37)(cid:206) 12212 <4(cid:37) (cid:146)(cid:147)(cid:96)(cid:40)(cid:102)(cid:69)(cid:281)(cid:37)(cid:48)(cid:112)(cid:33)l(cid:49)(cid:69)C(cid:22)(cid:96)(cid:50)(cid:108)(cid:37)(cid:122)(cid:20)(cid:66)C(cid:356)(cid:357). (cid:202)(cid:69)(cid:34)(cid:129)(cid:154) x2y22x8ya=0 (cid:110)(cid:85)(cid:37)x12y42 =17a(cid:37) (cid:146)(cid:147)(cid:69)(cid:70)(cid:36) 1,4(cid:37)(cid:120)(cid:121)(cid:36) 17a (cid:37) (cid:144)(cid:36)(cid:126)(cid:69)(cid:56)(cid:52)(cid:44)(cid:7)(cid:45)(cid:33)(cid:37)(cid:146)(cid:147)(cid:126)(cid:69)(cid:34)(cid:192)(cid:193)(cid:3)(cid:194)(cid:36)(cid:201)(cid:45)(cid:37)(cid:48) 122042 =5=2 17a(cid:37)(cid:116)(cid:85) a= 8(cid:37)(cid:122)(cid:20)(cid:66)D(cid:123)(cid:124). (cid:122)(cid:20)(cid:10)AD. 12(cid:25)(cid:26)2024·(cid:351)(cid:327)(cid:372)(cid:373)·(cid:52)(cid:328)(cid:31)(cid:182)(cid:183)E,F(cid:92)(cid:147)C1,2(cid:36)(cid:69)(cid:70)(cid:37) 2(cid:36)(cid:120)(cid:121)(cid:34)(cid:69)(cid:38)(cid:220)(cid:155)(cid:126)(cid:40)(cid:37)(cid:57)(cid:55)(cid:47)CE ^CF(cid:37)P uuur uuur (cid:92)EF (cid:34)(cid:106)(cid:40)(cid:37)(cid:150)(cid:101)(cid:102)(cid:3)(cid:98)3,0(cid:212)(cid:171)(cid:34)A,B(cid:126)(cid:40)(cid:37)(cid:55)(cid:47)PA×PB=0(cid:37)(cid:48)(cid:33)(cid:273)AB(cid:86)(cid:374)(cid:34)(cid:110)(cid:369)(cid:214)(cid:36)(cid:26) (cid:31) A(cid:25)3 B(cid:25)4 C(cid:25)5 D(cid:25)6 (cid:60)(cid:61)(cid:62)(cid:63)BCD (cid:60)(cid:64)(cid:65)(cid:63)(cid:202)(cid:182)(cid:183)(cid:85)(cid:80)P(cid:40)(cid:338)(cid:339)(cid:92)(cid:147)C(cid:36)(cid:69)(cid:70)(cid:37)1(cid:36)(cid:120)(cid:121)(cid:34)(cid:69)(cid:37)(cid:85)(cid:80) PD (cid:34)(cid:215)(cid:216)(cid:37)(cid:200)(cid:132)(cid:133)(cid:112)(cid:128)(cid:52)(cid:128)(cid:247)(cid:151)(cid:228)(cid:106)(cid:33) (cid:119)(cid:98)(cid:151)(cid:228)(cid:22)(cid:120)(cid:109)(cid:110)(cid:85)(cid:80) AB (cid:215)(cid:216)(cid:37)(cid:83)(cid:84)(cid:75)(cid:76)(cid:80)(cid:61)(cid:62)(cid:25) (cid:60)(cid:117)(cid:116)(cid:63)(cid:144)(cid:36)CE^CF,CE = CF = 2(cid:37) (cid:146)(cid:147) EF = CE 2 CF 2 =2(cid:37) 1 (cid:144)(cid:36)P(cid:92)EF (cid:106)(cid:40)(cid:37)(cid:146)(cid:147) CP = EF =1(cid:37) 2 (cid:146)(cid:147)P(cid:40)(cid:338)(cid:339)(cid:92)(cid:147)C(cid:36)(cid:69)(cid:70)(cid:37)1(cid:36)(cid:120)(cid:121)(cid:34)(cid:69)(cid:37) (cid:114)3,0(cid:36)(cid:40)D(cid:37)(cid:48) CD = (13)2(20)2 = 44 =2 2(cid:37) (cid:146)(cid:147) PD Î[2 21,2 21](cid:37) uuur uuur (cid:206)PA×PB=0(cid:37)A,B(cid:126)(cid:40)(cid:3)(cid:98)(cid:40)D3,0(cid:212)(cid:171)(cid:37) (cid:146)(cid:147)VPAB(cid:36)(cid:112)(cid:128)(cid:52)(cid:128)(cid:247)(cid:37)(cid:57)D(cid:36)(cid:151)(cid:228)AB(cid:106)(cid:40)(cid:37)(cid:48) AB =2 PD (cid:37) (cid:146)(cid:147) AB Î[4 22,4 22](cid:37) (cid:122)(cid:20)(cid:10)BCD(cid:25) 13(cid:25)(cid:26)2024·(cid:375)(cid:343)(cid:376)(cid:377)·(cid:52)(cid:328)(cid:31)(cid:182)(cid:183)(cid:112)(cid:33)l:axby1=0(cid:26)a,b(cid:153)(cid:301)(cid:54)(cid:36)0(cid:31)(cid:37)(cid:69)C:x2y22x=0(cid:37)(cid:48)(cid:26) (cid:31) A(cid:25)(cid:51)b22a=1(cid:54)(cid:37)(cid:112)(cid:33)l(cid:49)(cid:69)C(cid:50)(cid:45) B(cid:25)(cid:51)ab=2(cid:54)(cid:37)(cid:112)(cid:33)l(cid:49)(cid:69)C(cid:153)(cid:110)(cid:369)(cid:50)(cid:108) C(cid:25)(cid:51)a=1,b=1(cid:54)(cid:37)(cid:49)(cid:69)C(cid:201)(cid:45)(cid:57)(cid:49)(cid:112)(cid:33)l(cid:50)(cid:45)(cid:34)(cid:39)(cid:69)(cid:69)(cid:70)(cid:34)(cid:338)(cid:339)(cid:92)(cid:22)(cid:44)(cid:32)(cid:14)(cid:33) uuur uuur D(cid:25)(cid:51)a=1,b=1(cid:54)(cid:37)(cid:112)(cid:33)l(cid:49)(cid:81)(cid:82)(cid:225)(cid:50)(cid:108)(cid:98)A,B(cid:126)(cid:40)(cid:37)(cid:48)(cid:69)C(cid:38)(cid:101)(cid:102)(cid:40)P(cid:55)(cid:47)PA×PB=0(cid:60)(cid:61)(cid:62)(cid:63)ACD (cid:60)(cid:64)(cid:65)(cid:63)(cid:217)(cid:78)(cid:316)(cid:69)(cid:34)(cid:129)(cid:154)(cid:16)(cid:36)(cid:82)(cid:35)(cid:135)(cid:37)(cid:109)(cid:110)(cid:85)(cid:71)(cid:69)(cid:70)(cid:81)(cid:82)(cid:49)(cid:120)(cid:121)(cid:37)(cid:79)(cid:80)(cid:69)(cid:70)(cid:71)(cid:112)(cid:33)(cid:34)(cid:72)(cid:73)(cid:109)(cid:110)(cid:75)(cid:76)A(cid:37)(cid:140) (cid:141)(cid:284)(cid:286)(cid:214)(cid:75)(cid:76)B(cid:37)(cid:67)(cid:68)(cid:32)(cid:14)(cid:33)(cid:34)(cid:96)(cid:97)(cid:75)(cid:76)C(cid:37)(cid:79)(cid:80)(cid:147)AB(cid:36)(cid:112)(cid:121)(cid:34)(cid:69)(cid:34)(cid:129)(cid:154)(cid:37)(cid:109)(cid:110)(cid:75)(cid:76)(cid:126)(cid:69)(cid:50)(cid:108)(cid:37)(cid:210)(cid:84)(cid:75)(cid:76) D. (cid:60)(cid:117)(cid:116)(cid:63)(cid:69)C:x2y22x=0(cid:109)x12y2 =1(cid:37)(cid:69)(cid:70)(cid:36)C1,0(cid:37)(cid:120)(cid:121)r=1(cid:77) a1 a1 a1 (cid:212)(cid:98)A(cid:10)(cid:150)b22a=1(cid:37)(cid:48)(cid:69)(cid:70)(cid:71)(cid:112)(cid:33)(cid:34)(cid:72)(cid:73)d = = = =1=r(cid:37) a2b2 a22a1 a12 (cid:146)(cid:147)(cid:112)(cid:33)l(cid:49)(cid:69)C(cid:50)(cid:45)(cid:37)(cid:122)A(cid:123)(cid:124)(cid:77) 1 (cid:212)(cid:98)B(cid:10)(cid:51)a=0(cid:37)b=2(cid:54)(cid:55)(cid:47)ab=2(cid:37)(cid:104)(cid:54)(cid:112)(cid:33)(cid:129)(cid:154)(cid:36)y= (cid:37) 2 1 (cid:48)(cid:69)(cid:70)(cid:71)(cid:112)(cid:33)(cid:34)(cid:72)(cid:73)(cid:36) 1 3(cid:37)(cid:69)C (cid:107)(cid:69)C (cid:50)(cid:73)(cid:37)B(cid:123)(cid:124)(cid:77) 1 2 1 2 (cid:212)(cid:98)C(cid:37)(cid:69)C (cid:3)(cid:98)x(cid:225)(cid:212)(cid:171)(cid:34)(cid:69)(cid:36)C :(x1)2(y2)2 =1(cid:37)C (1,2)(cid:37)(cid:148)(cid:113)C C (cid:108)x(cid:98)(cid:40)P(cid:37)(cid:148)(cid:113)PC (cid:37) 1 0 0 0 2 1 1 1 (cid:202)(cid:69)(cid:34)(cid:103)(cid:131)(cid:85)(cid:37) PM  PN ³ PC 1 PC  3= PC  PC 1 3 1 2 0 2 ³|C C |1 3=2 101 3(cid:37)(cid:51)(cid:57)(cid:58)(cid:51)(cid:40)P(cid:49)P(cid:234)(cid:133)(cid:37) 0 2 1 (cid:57)M,N(cid:92)(cid:33)(cid:273)PC,PC (cid:64)(cid:157)(cid:49)(cid:69)C (cid:107)(cid:69)C (cid:34)(cid:108)(cid:40)(cid:54)(cid:213)(cid:119)(cid:9)(cid:37)C(cid:356)(cid:357)(cid:77) 1 1 1 2 1 2 (cid:212)(cid:98)D(cid:37)(cid:114)(cid:40)P(t,0)(cid:37)(cid:41)(cid:40)P(cid:34)(cid:69)C (cid:34)(cid:45)(cid:33)(cid:86)|PA|= PC2AC2 = (t1)2221³ 3(cid:37) 1 1 1 (cid:51)(cid:57)(cid:58)(cid:51)t=1(cid:37)(cid:109)P(1,0)(cid:54)(cid:213)(cid:119)(cid:9)(cid:37)D(cid:123)(cid:124). (cid:122)(cid:20)(cid:10)BD 15(cid:25)(cid:26)2024·(cid:382)(cid:326)(cid:383)(cid:377)·(cid:137)(cid:328)(cid:31)(cid:182)(cid:183)(cid:69) C :x2y2 =6(cid:49)(cid:69) C :x2y22xa=0(cid:50)(cid:108)(cid:98) A,B(cid:126)(cid:40)(cid:25)(cid:150) 1 2 S =2S (cid:37)(cid:48)(cid:303)(cid:13)a(cid:34)(cid:214)(cid:110)(cid:147)(cid:92)(cid:26) (cid:31) △C1AB △C2AB 22 14 A(cid:25)10 B(cid:25)2 C(cid:25) D(cid:25) 3 3 (cid:60)(cid:61)(cid:62)(cid:63)BD (cid:60)(cid:64)(cid:65)(cid:63) (cid:67)(cid:68)(cid:21)(cid:155)(cid:37)(cid:202)(cid:44)(cid:205)(cid:110)(cid:85)(cid:139)AB(cid:146)(cid:102)(cid:34)(cid:112)(cid:33)(cid:129)(cid:154)(cid:37)(cid:88)(cid:89)(cid:316)S =2S (cid:100)(cid:16)(cid:36)(cid:69)(cid:70)(cid:71)(cid:112)(cid:33)AB(cid:34)(cid:72)(cid:73)(cid:3)(cid:194)(cid:37) △C1AB △C2AB(cid:185)(cid:80)(cid:129)(cid:154)(cid:37)(cid:161)(cid:384)(cid:333)(cid:87)(cid:37)(cid:109)(cid:110)(cid:85)(cid:71)(cid:132)(cid:365). (cid:60)(cid:117)(cid:116)(cid:63)(cid:202)(cid:21)(cid:155)(cid:110)(cid:85)(cid:139)AB(cid:146)(cid:102)(cid:34)(cid:112)(cid:33)(cid:129)(cid:154)(cid:36)C C :2x6a=0(cid:37) 1 2 (cid:144)(cid:36)(cid:69)C :x2y2 =6(cid:37)(cid:69)(cid:70)C 0,0(cid:37) 1 1 (cid:69)C :x2y22xa=0(cid:37)(cid:69)(cid:70)C 1,0(cid:37) 2 2 (cid:114)(cid:69)(cid:70)C 0,0(cid:49)(cid:69)(cid:70)C 1,0(cid:71)(cid:112)(cid:33)AB(cid:34)(cid:72)(cid:73)(cid:64)(cid:157)(cid:36)d ,d (cid:37) 1 2 1 2 1 1 (cid:144)(cid:36)S =2S (cid:37)(cid:109) AB ×d =2´ AB ×d (cid:37) △C1AB △C2AB 2 1 2 2 6a 4a (cid:146)(cid:147)d =2d (cid:37)(cid:206)d = ,d = (cid:37) 1 2 1 2 2 2 6a 4a (cid:109) =2´ (cid:37)(cid:16)(cid:385)(cid:110)(cid:85)3a220a28=0(cid:37) 2 2 14 (cid:109)3a14a2=0(cid:37)(cid:116)(cid:85)a=2(cid:191)a= . 3 (cid:122)(cid:20)(cid:10)BD 16(cid:25)(cid:26)2024·(cid:382)(cid:326)(cid:386)(cid:387)·(cid:52)(cid:328)(cid:31)(cid:182)(cid:183)M (cid:37)N (cid:36)(cid:69)x2y2 =4(cid:38)(cid:34)(cid:126)(cid:59)(cid:39)(cid:40)(cid:37)(cid:40)P1,1(cid:37)(cid:57)PM ^PN (cid:37)(cid:48) (cid:26) (cid:31) A(cid:25) PM =2 2 max B(cid:25) MN =2 2 3 max 2 2 æ 1ö æ 1ö 3 C(cid:25)VPMN(cid:201)(cid:113)(cid:69)(cid:69)(cid:70)(cid:34)(cid:338)(cid:339)(cid:129)(cid:154)(cid:36) çx ÷ çy ÷ = è 2ø è 2ø 2 2 2 æ 5ö æ 5ö 1 D(cid:25)VPMN(cid:234)(cid:70)(cid:34)(cid:338)(cid:339)(cid:129)(cid:154)(cid:36) çx ÷ çy ÷ = è 6ø è 6ø 6 (cid:60)(cid:61)(cid:62)(cid:63)ABC (cid:60)(cid:64)(cid:65)(cid:63)(cid:67)(cid:68)(cid:69)(cid:34)(cid:103)(cid:131)(cid:37)(cid:110)(cid:85)(cid:75)(cid:96)A(cid:123)(cid:124)(cid:77)(cid:51)(cid:33)(cid:273)MN(cid:34)(cid:106)(cid:46)(cid:33)(cid:388)(cid:41)(cid:40)P(cid:54)(cid:37)(cid:104)(cid:54) MN (cid:213)(cid:85)(cid:314)(cid:214)(cid:37)(cid:132)(cid:133)(cid:69) (cid:34)(cid:103)(cid:131)(cid:37)(cid:110)(cid:75)(cid:96)B(cid:123)(cid:124)(cid:77)(cid:114)VPMN(cid:34)(cid:201)(cid:113)(cid:69)(cid:34)(cid:69)(cid:70)(cid:36)C(x,y)(cid:37)(cid:67)(cid:68) CP = CM (cid:37)(cid:79)(cid:85)(cid:338)(cid:339)(cid:129)(cid:154)(cid:37)(cid:110)(cid:75)(cid:96)(cid:147) C(cid:123)(cid:124)(cid:77)(cid:114)VPMN(cid:34)(cid:234)(cid:70)(cid:36)(cid:40)G(x ,y )(cid:37)(cid:132)(cid:133)C(cid:66)(cid:37)(cid:79)(cid:85)(cid:179)(cid:338)(cid:339)(cid:129)(cid:154)(cid:37)(cid:110)(cid:75)(cid:96)D(cid:356)(cid:357). G G (cid:60)(cid:117)(cid:116)(cid:63)(cid:144)(cid:36)(cid:69)x2y2 =4(cid:37)(cid:110)(cid:85)(cid:69)(cid:70)O(0,0)(cid:37)(cid:120)(cid:121)(cid:36)r=2(cid:37)(cid:57)(cid:40)P1,1(cid:102)(cid:69)(cid:281)(cid:37) (cid:212)(cid:98)A(cid:106)(cid:37)(cid:202) PO = 2(cid:37)(cid:67)(cid:68)(cid:69)(cid:34)(cid:103)(cid:131)(cid:37)(cid:110)(cid:85)r PO £ PM £r PO (cid:37) (cid:109)2 2 £ PM £2 2(cid:37)(cid:109) PM Î[2 2,2 2](cid:37) (cid:146)(cid:147) PM (cid:34)(cid:314)(cid:242)(cid:214)(cid:36)2 2(cid:37)(cid:146)(cid:147)A(cid:123)(cid:124)(cid:77) (cid:212)(cid:98)B(cid:106)(cid:37)(cid:144)(cid:36)PM ^PN (cid:37)(cid:51)(cid:33)(cid:273)MN(cid:34)(cid:106)(cid:46)(cid:33)(cid:388)(cid:41)(cid:40)P(cid:54)(cid:37)(cid:104)(cid:54) MN (cid:213)(cid:85)(cid:314)(cid:214)(cid:37) (cid:211)(cid:158)(cid:146)(cid:178)(cid:37)(cid:110)(cid:85)M( 3,1),N(1, 3)(cid:54)(cid:37)(cid:110)(cid:85) MN =2 2 3(cid:37) maxM( 3,1),N(1, 3)(cid:54)(cid:37)(cid:110)(cid:85) MN =2 2 3 (cid:37)(cid:146)(cid:147)B(cid:123)(cid:124)(cid:77) min (cid:212)(cid:98)C(cid:106)(cid:37)(cid:114)VPMN(cid:34)(cid:201)(cid:113)(cid:69)(cid:34)(cid:69)(cid:70)(cid:36)C(x,y)(cid:37)(cid:48) CP = CM (cid:37) (cid:48)(cid:56)(x1)2(y1)2 =4(x2y2)(cid:37)(cid:110)(cid:85)2x22y22x2y2=0(cid:37) 1 1 3 (cid:109)(x )2(y )2 = (cid:37)(cid:146)(cid:147)C(cid:123)(cid:124)(cid:77) 2 2 2 (cid:212)(cid:98)D(cid:106)(cid:37)(cid:114)VPMN(cid:34)(cid:234)(cid:70)(cid:36)(cid:40)G(x ,y )(cid:37)(cid:48)3x =x x 1,3y = y y 1(cid:37) G G G M N G M N 1 1 3 (cid:202)C(cid:66)(cid:183)VPMN(cid:34)(cid:201)(cid:113)(cid:69)(cid:34)(cid:69)(cid:70)(cid:40)C(cid:34)(cid:338)(cid:339)(cid:129)(cid:154)(cid:36)(x )2(y )2 = (cid:37) 2 2 2 (cid:57)(cid:40)C(cid:36)MN(cid:34)(cid:106)(cid:40)(cid:37)(cid:109)x x =2x,y y =2y(cid:37)(cid:146)(cid:147)3x =2x1,3y =2y1(cid:37) M N M N G G 3x 1 1 3y 1 1 3 2 2 2 (cid:109)( G  )2( G  )2 = (cid:37)(cid:109)(x )2(y )2 = (cid:37)(cid:146)(cid:147)D(cid:356)(cid:357). 2 2 2 2 2 3 3 3 (cid:122)(cid:20)(cid:10)ABC. (cid:52)(cid:23)(cid:187)(cid:188)(cid:21) 17(cid:25)(cid:26)2024·(cid:389)(cid:352)(cid:390)(cid:391)·(cid:52)(cid:328)(cid:31)(cid:182)(cid:183)(cid:69)C(cid:388)(cid:41)A2,0(cid:37)B0,2(cid:37)C2,4(cid:52)(cid:40)(cid:37) (cid:26)i(cid:31)(cid:48)(cid:69)C(cid:34)(cid:82)(cid:35)(cid:129)(cid:154)(cid:36) (cid:77) (cid:26)ii(cid:31)(cid:150)(cid:112)(cid:33)AB(cid:3)(cid:98)y=a(cid:212)(cid:171)(cid:34)(cid:112)(cid:33)(cid:49)(cid:69)C(cid:56)(cid:7)(cid:53)(cid:40)(cid:37)(cid:48)a(cid:34)(cid:213)(cid:214)(cid:215)(cid:216)(cid:92) . (cid:60)(cid:61)(cid:62)(cid:63) (x2)2(y2)2 =4 é1 2,1 2ù ë û (cid:60)(cid:64)(cid:65)(cid:63)(cid:188)1(cid:10)(cid:114)(cid:69)(cid:34)(cid:22)(cid:280)(cid:129)(cid:154)x2y2DxEyF =0(cid:37)(cid:200)(cid:161)(cid:384)(cid:52)(cid:59)(cid:40)(cid:85)(cid:71)(cid:129)(cid:154)(cid:304)(cid:37)(cid:116)(cid:80)(cid:109)(cid:110)(cid:77)(cid:188)2(cid:10)(cid:217)(cid:78) (cid:79)(cid:80)(cid:112)(cid:33)AB(cid:34)(cid:129)(cid:154)(cid:37)(cid:200)(cid:79)(cid:80)(cid:179)(cid:212)(cid:171)(cid:129)(cid:154)(cid:37)(cid:67)(cid:68)(cid:112)(cid:33)(cid:49)(cid:69)(cid:34)(cid:192)(cid:193)(cid:3)(cid:194)(cid:85)(cid:71)(cid:153)(cid:119)(cid:135)(cid:37)(cid:116)(cid:80)(cid:109)(cid:110). (cid:60)(cid:117)(cid:116)(cid:63)(cid:67)(cid:68)(cid:21)(cid:155)(cid:110)(cid:114)(cid:69)(cid:34)(cid:129)(cid:154)(cid:36)x2y2DxEyF =0(cid:37)(cid:179)(cid:106)D2E24F >0(cid:37) ì42DF =0 ï (cid:48)í42EF =0 (cid:37)(cid:116)(cid:85)D=4,E=4,F =4(cid:37) ï î4162D4EF =0 \(cid:69)C(cid:34)(cid:129)(cid:154)(cid:36)x2y24x4y4=0(cid:37) (cid:109)(cid:69)C(cid:34)(cid:82)(cid:35)(cid:129)(cid:154)(cid:36)(x2)2(y2)2 =4(cid:77) 20 (cid:202)(cid:21)(cid:155)(cid:183)(cid:37)(cid:112)(cid:33)AB(cid:34)(cid:151)(cid:152)(cid:36)k = =1(cid:37) AB 02(cid:112)(cid:33)AB(cid:129)(cid:154)(cid:36)y=x2(cid:37)(cid:49)y=a(cid:34)(cid:108)(cid:40)(cid:36)(2a,a)(cid:37) (cid:146)(cid:147)(cid:112)(cid:33)AB(cid:3)(cid:98)y=a(cid:212)(cid:171)(cid:34)(cid:112)(cid:33)(cid:34)(cid:151)(cid:152)(cid:36)k=1(cid:37) (cid:122)(cid:212)(cid:171)(cid:112)(cid:33)(cid:34)(cid:129)(cid:154)(cid:36)ya=1(x2a)(cid:37)(cid:109)xy22a=0(cid:37) (cid:202)(x2)2(y2)2 =4(cid:183)(cid:37)(cid:69)(cid:70)(cid:36)(2,2)(cid:37)(cid:120)(cid:121)(cid:36)2(cid:37) (cid:144)(cid:36)(cid:212)(cid:171)(cid:112)(cid:33)(cid:49)(cid:69)(cid:56)(cid:7)(cid:53)(cid:40)(cid:37) 2222a (cid:146)(cid:147) £2(cid:37) 11 (cid:116)(cid:85)1 2£a£1 2(cid:37)(cid:109)(cid:303)(cid:13)a(cid:34)(cid:213)(cid:214)(cid:215)(cid:216)(cid:36)[1 2,1 2]. (cid:122)(cid:61)(cid:62)(cid:36)(cid:10)(x2)2(y2)2 =4(cid:77)é1 2,1 2ù. ë û 18(cid:25)(cid:26)2024·(cid:392)(cid:393)(cid:107)(cid:170)·(cid:52)(cid:328)(cid:31)(cid:182)(cid:183)(cid:69)C(cid:147)(cid:40)1,1(cid:36)(cid:69)(cid:70)(cid:37)(cid:57)(cid:49)(cid:112)(cid:33)mxy2m=0mÎR (cid:50)(cid:45)(cid:37)(cid:48)(cid:55)(cid:47)(cid:147)(cid:38) (cid:44)(cid:205)(cid:34)(cid:69)C(cid:34)(cid:120)(cid:121)(cid:314)(cid:242)(cid:54)(cid:37)(cid:69)C(cid:34)(cid:82)(cid:35)(cid:129)(cid:154)(cid:36) (cid:25) (cid:60)(cid:61)(cid:62)(cid:63)x12y12 =2 (cid:60)(cid:64)(cid:65)(cid:63)(cid:78)(cid:79)(cid:85)(cid:112)(cid:33)mxy2m=0(cid:41)(cid:96)(cid:40)A2,0(cid:37)(cid:69)C(cid:34)(cid:120)(cid:121)(cid:314)(cid:242)(cid:54)(cid:37)(cid:109)(cid:36)(cid:69)(cid:70)1,1(cid:107)(cid:40)2,0(cid:34)(cid:72)(cid:73)(cid:37) (cid:109)(cid:110)(cid:79)(cid:85)(cid:120)(cid:121)(cid:37)(cid:83)(cid:84)(cid:79)(cid:85)(cid:69)C(cid:34)(cid:82)(cid:35)(cid:129)(cid:154). (cid:60)(cid:117)(cid:116)(cid:63)(cid:112)(cid:33)mxy2m=0(cid:37)(cid:110)(cid:16)(cid:36)mx2y=0(cid:37) ìx2=0 ìx=2 (cid:146)(cid:147)í (cid:37)(cid:116)(cid:85)í (cid:37)(cid:146)(cid:147)(cid:112)(cid:33)(cid:41)(cid:96)(cid:40)A2,0(cid:37) îy=0 îy=0 (cid:51)CA(cid:49)(cid:112)(cid:33)mxy2m=0(cid:46)(cid:112)(cid:54)(cid:37)(cid:69)C(cid:34)(cid:120)(cid:121)(cid:314)(cid:242)(cid:37)(cid:120)(cid:121)(cid:36) 212012 = 2(cid:37) (cid:146)(cid:147)(cid:69)C(cid:34)(cid:82)(cid:35)(cid:129)(cid:154)(cid:36)x12y12 =2. (cid:122)(cid:61)(cid:62)(cid:36)(cid:10)x12y12 =2. 19(cid:25)(cid:26)2024·(cid:281)(cid:394)(cid:160)(cid:395)(cid:107)(cid:396)(cid:284)·(cid:137)(cid:328)(cid:31)(cid:40)P1,a(cid:3)(cid:98)(cid:112)(cid:33)xy=0(cid:34)(cid:212)(cid:171)(cid:40)(cid:102)(cid:69)(x2)2(y4)2 =13(cid:281)(cid:37)(cid:48) (cid:303)(cid:13)a(cid:34)(cid:213)(cid:214)(cid:215)(cid:216)(cid:92) (cid:25) (cid:60)(cid:61)(cid:62)(cid:63)4,0 (cid:60)(cid:64)(cid:65)(cid:63)(cid:67)(cid:68)(cid:21)(cid:155)(cid:140)(cid:141)(cid:225)(cid:212)(cid:171)(cid:34)(cid:103)(cid:131)(cid:87)(cid:80)(cid:212)(cid:171)(cid:40)Q(cid:34)(cid:81)(cid:82)(cid:37)(cid:132)(cid:133)(cid:40)Q(cid:102)(cid:182)(cid:183)(cid:69)(cid:34)(cid:281)(cid:397)(cid:37)(cid:162)(cid:95)(cid:3)(cid:98)a(cid:34)(cid:153)(cid:119) (cid:135)(cid:37)(cid:116)(cid:80)(cid:303)(cid:13)a(cid:34)(cid:213)(cid:214)(cid:215)(cid:216)(cid:25) ìm1 na  =0 (cid:60)(cid:117)(cid:116)(cid:63)(cid:114)Qm,n(cid:49)P1,a(cid:3)(cid:98)(cid:112)(cid:33)xy=0(cid:212)(cid:171)(cid:37)(cid:48) ï ï í 2 2 (cid:37)(cid:116)(cid:85) ì í m=a (cid:37)(cid:109)Qa,1(cid:37) ï an =1 în=1 ïî 1m (cid:144)(cid:36)Qa,1(cid:102)(cid:69)(x2)2(y4)2 =13(cid:34)(cid:281)(cid:397)(cid:37) (cid:146)(cid:147)(a2)2(14)2 <13(cid:37)(cid:116)(cid:85)-4