四川省成都市第七中学2024-2025学年高二上学期11月期中考试数学PDF版含解析（可编辑）_2024-2025高二（7-7月题库）_2024年11月试卷

成都七中高 2026 届高二上半期数学考试题 一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一 项是符合题目要求的。 1.以点C1,5为圆心，并与x轴相切的圆的标准方程是（ ） A．(x1)2 (y5)2 9 B．(x1)2(y5)2 16 C．(x1)2(y5)2 9 D．(x1)2(y5)2 25 2.若a=(-1,2,1),b=(1,3,2)，则(a+b)(2ab)=（ ） A.2 B. 5 C.21 D.26 3．“m3”是“直线l :m1x2y10与直线l :3xmy10平行”的（ ） 1 2 A．充要条件 B．必要不充分条件C．充分不必要条件D．既不充分也不必要条件 4.已知椭圆的两个焦点坐标分别为(−𝟐,𝟎),(𝟐,𝟎)，且椭圆上的点P到两焦点的距离之和为8， 则椭圆的标准方程为（ ） 𝒙𝟐 𝒚𝟐 𝒙𝟐 𝒙𝟐 𝒙𝟐 𝒚𝟐 𝒚𝟐 𝒙𝟐 A. + =𝟏 B. + =𝟏 C. + =𝟏 D. + =𝟏 𝟑𝟔 𝟐𝟕 𝟏𝟎 𝟔 𝟏𝟔 𝟏𝟐 𝟏𝟔 𝟏𝟐 5.已知从2名男生和2名女生中任意选出两人参加高中生创新能力大赛，则选出的两人恰好是 一名男生和一名女生的概率是（ ） 2 1 1 1 A. B. C. D. 3 2 3 4 6.如果一组数据的频率分布直方图在右边“拖尾”（如下图），则下列说法一定错误的是（ ） A．数据中可能存在极端大的值 B．这组数据是不对称的 C．数据中众数一定不等于中位数 D．数据的平均数大于中位数 7.在正四棱柱ABCDABCD 中，AA 2AB4，点E在线段CC 上，且CC 4CE，点F 为 1 1 1 1 1 1 1 BD中点,则点D 到直线EF的距离（ ） 1 √𝟏𝟏𝟒 √𝟏𝟏𝟒 √𝟕𝟒 √𝟕𝟒 A. B. C. C. 𝟑 𝟐 𝟐 𝟑 8.已知O(0,0),Q0,1，直线l :kxy2k40，直线l :xky4k20，若P为l ,l 的 1 2 1 2 交点，则2 PO  PQ 的最小值为（ ） A．63 2 B． 37 C．93 2 D．3 6 二、多项选择题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合 题目要求．全部选对的得6分，部分选对的得部分分，有选错的得0分． 9.成都七中高新校区高二年级14个班团体操比赛成绩(满分100分)从小到大排序依次 为：88,89,90,90,90,90,91,91,91,92,92,93,93,94(单位分),则下列说法正确的是( ) 18 A.众数为90B.中位数为91.5 C.第80百分位数为92 D.方差为 7 1 {#{QQABLYIAogAgAAJAAQgCQQFQCkAQkgAACQgOwBAEMAIBCRNABAA=}#}{#{QQABLYIAogAgAAJAAQgCQQFQCkAQkgAACQgOwBAEMAIBCRNABAA=}#}四、解答题：本题共5小题，共77分．其中15题13分，16—17题15分，18—19题17 分。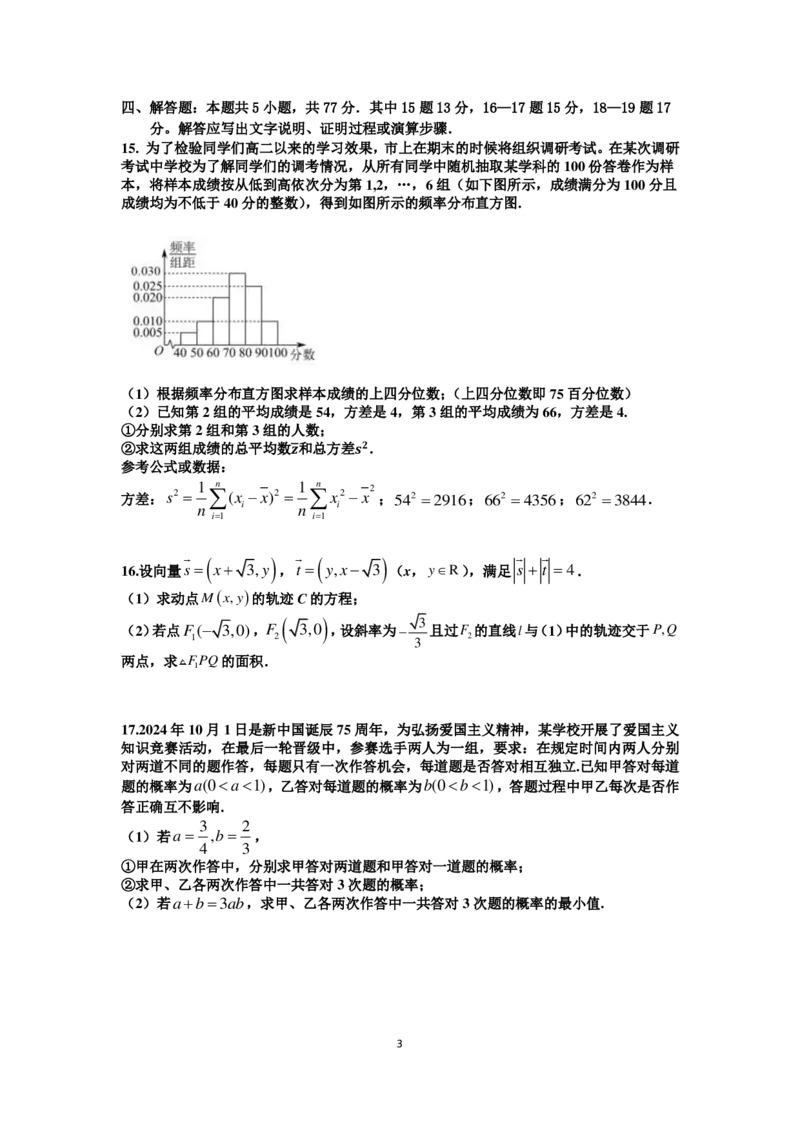解答应写出文字说明、证明过程或演算步骤． 15. 为了检验同学们高二以来的学习效果，市上在期末的时候将组织调研考试。在某次调研 考试中学校为了解同学们的调考情况，从所有同学中随机抽取某学科的100份答卷作为样 本，将样本成绩按从低到高依次分为第1,2，…，6组（如下图所示，成绩满分为100分且 成绩均为不低于40分的整数），得到如图所示的频率分布直方图. （1）根据频率分布直方图求样本成绩的上四分位数；（上四分位数即75百分位数） （2）已知第2组的平均成绩是54，方差是4，第3组的平均成绩为66，方差是4. ①分别求第2组和第3组的人数； ②求这两组成绩的总平均数𝒛和总方差𝒔𝟐． 参考公式或数据： 1 n 1 n 方差：s2  (x x)2  x2 x 2 ；542 2916；662 4356；622 3844. n i n i i1 i1     16.设向量s x 3,y ，t  y,x 3 （x，yR），满足 s  t 4． （1）求动点Mx,y的轨迹C的方程；   3 （2）若点F( 3,0)，F 3,0 ，设斜率为 且过F 的直线l与（1）中的轨迹交于P,Q 1 2 3 2 两点，求 FPQ的面积． 1 17.2024年10月1日是新中国诞辰75周年，为弘扬爱国主义精神，某学校开展了爱国主义 知识竞赛活动，在最后一轮晋级中，参赛选手两人为一组，要求：在规定时间内两人分别 对两道不同的题作答，每题只有一次作答机会，每道题是否答对相互独立.已知甲答对每道 题的概率为a(0a1)，乙答对每道题的概率为b(0b1)，答题过程中甲乙每次是否作 答正确互不影响. 3 2 （1）若a ,b ， 4 3 ①甲在两次作答中，分别求甲答对两道题和甲答对一道题的概率； ②求甲、乙各两次作答中一共答对3次题的概率； （2）若ab3ab，求甲、乙各两次作答中一共答对3次题的概率的最小值. 3 {#{QQABLYIAogAgAAJAAQgCQQFQCkAQkgAACQgOwBAEMAIBCRNABAA=}#}18. 已 知 圆 O :x2  y2 4 ， 圆 O 与 圆 O 关 于 直 线 y x2 对 称 ， 圆 1 2 1 O :(x1)2 (y4)2 9. 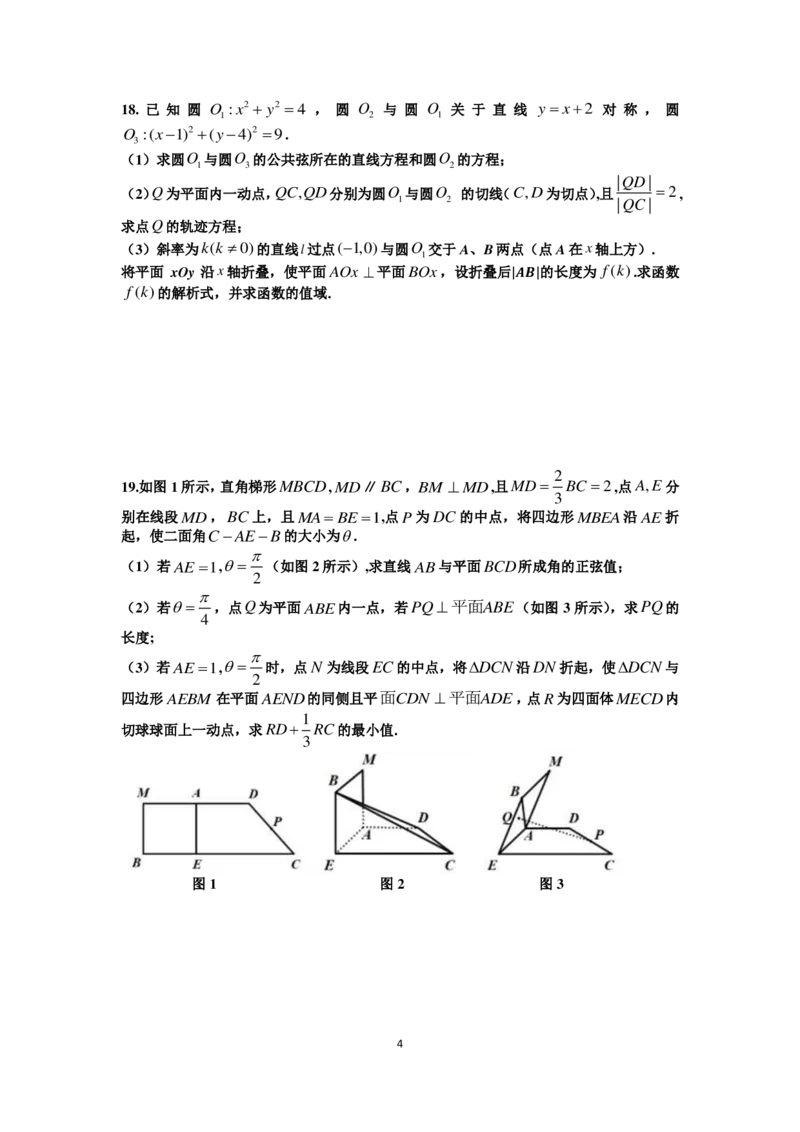3 （1）求圆O 与圆O 的公共弦所在的直线方程和圆O 的方程； 1 3 2 |QD| （2）Q为平面内一动点，QC,QD分别为圆O 与圆O 的切线（C,D为切点）,且 2, 1 2 |QC| 求点Q的轨迹方程； （3）斜率为k(k 0)的直线l过点(1,0)与圆O 交于A、B两点（点A在x轴上方）. 1 将平面 xOy 沿x轴折叠，使平面AOx 平面BOx，设折叠后|𝑨𝑩|的长度为 f(k).求函数 f(k)的解析式，并求函数的值域. 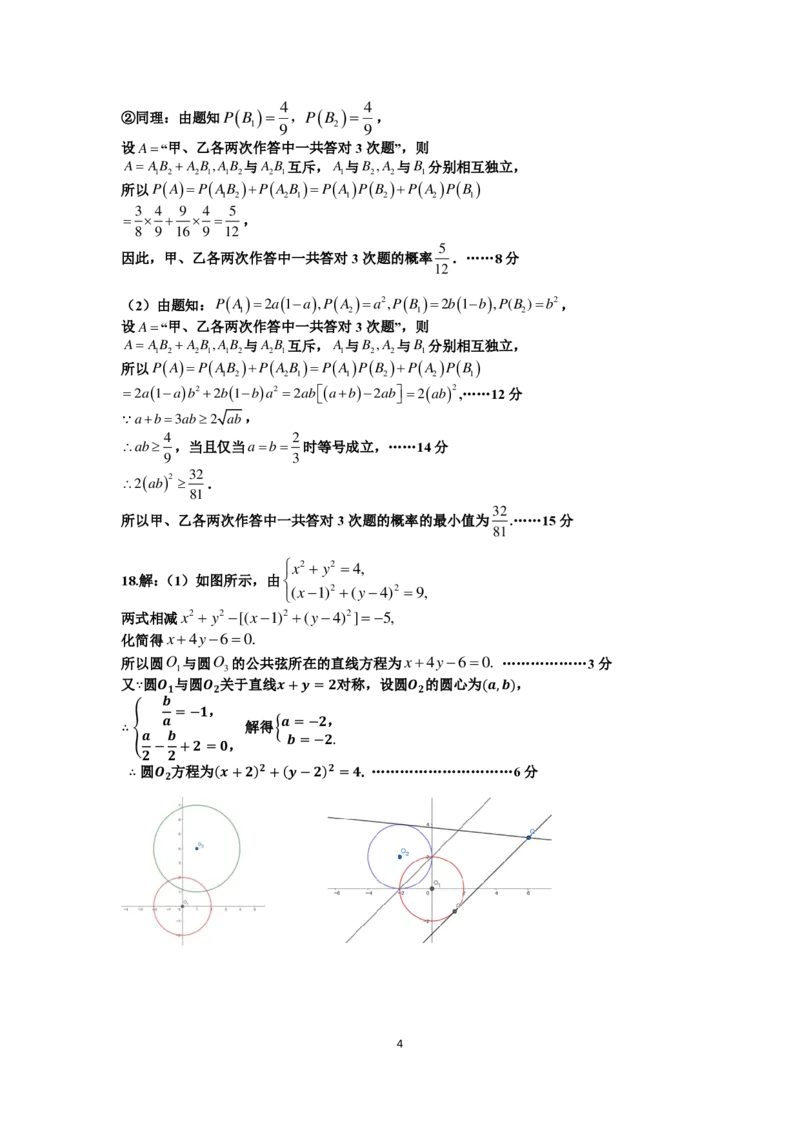2 19.如图1所示，直角梯形MBCD,MD∥BC，BM MD,且MD BC 2,点A,E分 3 别在线段MD，BC上，且MABE1,点P为DC 的中点，将四边形MBEA沿AE折 起，使二面角CAEB的大小为.  （1）若AE 1, （如图2所示）,求直线AB与平面BCD所成角的正弦值； 2  （2）若 ，点Q为平面ABE内一点，若PQ平面ABE（如图 3 所示），求PQ的 4 长度;  （3）若AE 1, 时，点N 为线段EC的中点，将DCN沿DN折起，使DCN与 2 四边形AEBM 在平面AEND的同侧且平面CDN 平面ADE，点R为四面体MECD内 1 切球球面上一动点，求RD RC的最小值. 3 图1 图2 图3 4 {#{QQABLYIAogAgAAJAAQgCQQFQCkAQkgAACQgOwBAEMAIBCRNABAA=}#}成都七中高 2026 届高二上期半期数学考试题（参考答案） 一．选择题 DBAC ACAB 8.解析：直线l :kx−y+2k+4=0过定点M(−2,4),直线l :x+ky+4k+2=0过定点N(−2,−4), 1 2 且直线l与直线l 垂直，所以点P的轨迹是以MN为直径的圆，除去点N(−2,−4), 1 2 故圆心是C(−2,0),半径为4.则点P的方程是(x+2)2+y2 =16(y−4). 令2 PO = PA,可得点A(6,0),则2 PO + PQ = PA+ PQ 2 AQ = （0−6）2+（1−0）2 = 37. 二.多项选择题 9.答案：AD 解析：易知：众数为90；中位数为91;第80百分位数为140.8=11.2(故取第十二个数为93); 1 18 易得x=91,则方差为 (32+22+124+023+122+222+32)= . 14 7 10.答案：ABD 解：(A)体对角线B D⊥ BC ,又 BC //GE,可知B D ⊥GE,故A正确. 1 1 1 1 (B)异面直线AA和DB的距离,几何法向量法皆可求得PQ = 2, 1 1 min 分别以DA,DC,DD所在的直线为x轴、y轴、z轴建立空间直角坐标系如图. 1 AA =(0,0,2),DB =(2,2,2),设n=(x, y,z)为异面直线AA和DB的公垂线的 1 1 1 1  nAA =0, AB n 一个方向向量, 1 取n=(1,−1,0),PQ = 1 1 = 2,故B正确. min nDB =0, n 1 (C)EF =(−2,−1,1),EG =(−2,0,2),设n =(x , y ,z )为平面EFG的一个法向量, 1 1 1 1  n EF =0,  1 取n =(1,−1,1),取n =(0,1,0)为平面ADD A的一个法向量. 1 2 1 1 n EG =0, 1 n n 3 6 cos n ,n = 1 2 = ,故其正弦值为 ,则C错误. 1 2 n n 3 3 1 2 (D)如图延展平面易知平面EFG被正方体截得多边形为正六边形,则其面积为 3 ( 2)26=3 3,则D正确. 4 1 {#{QQABLYIAogAgAAJAAQgCQQFQCkAQkgAACQgOwBAEMAIBCRNABAA=}#}{#{QQABLYIAogAgAAJAAQgCQQFQCkAQkgAACQgOwBAEMAIBCRNABAA=}#}②两组成绩的总平均数为𝐳= 𝟏𝟎×𝟓𝟒+𝟔𝟔×𝟐𝟎 =𝟔𝟐，…… ………………………9分 𝟏𝟎+𝟐𝟎 设成绩在[𝟓𝟎,𝟔𝟎)中10人的分数分别为𝐱 ，𝐱 ，𝐱 ，…，𝐱 ； 𝟏 𝟐 𝟑 𝟏𝟎 成绩在[𝟔𝟎,𝟕𝟎)中20人的分数分别为𝐲 ，𝐲 ，𝐲 ，…，𝐲 ， 𝟏 𝟐 𝟑 𝟐𝟎 则由题意可得，𝐱 𝟏 𝟐+𝐱 𝟐 𝟐+⋯+𝐱 𝟏 𝟐 𝟎−𝟓𝟒𝟐 =𝟒，𝐲 𝟏 𝟐+𝐲 𝟐 𝟐+⋯+𝐲 𝟐 𝟐 𝟎−𝟔𝟔𝟐 =𝟒， 𝟏𝟎 𝟐𝟎 即𝐱𝟐+𝐱𝟐+⋯+𝐱𝟐 =𝟐𝟗𝟐𝟎𝟎，𝐲𝟐+𝐲𝟐+⋯+𝐲𝟐 =𝟖𝟕𝟐𝟎𝟎， ………………11分 𝟏 𝟐 𝟏𝟎 𝟏 𝟐 𝟐𝟎 所 以𝐬𝟐 = 𝟏 (𝐱𝟐+𝐱𝟐+⋯+𝐱𝟐 +𝐲𝟐+𝐲𝟐+⋯+𝐲𝟐 )−𝐳 𝟐 = 𝟏 ×(𝟐𝟗𝟐𝟎𝟎+𝟖𝟕𝟐𝟎𝟎)− 𝟏𝟎+𝟐𝟎 𝟏 𝟐 𝟏𝟎 𝟏 𝟐 𝟐𝟎 𝟑𝟎 𝟔𝟐𝟐 =𝟑𝟔， 所以两组成绩的总平均数是62，总方差是36．……………………………………………13分 16. 解：（1）由 3 s + t = 4 得 (x+ 3)2 + y2 + (x− 3)2+ y2 =4，………………2分 由椭圆定义知： ( ) ( ) 点M(x,y)是以 − 3,0 、 3,0 为焦点，长轴为4的椭圆，………………4分 ∴点M(x,y)的轨迹C的方程为： x 4 2 + y 2 = 1 ．……………………………………6分 （2）∵ F 1 ( − 3 , 0 ) F 2 ( 3 , 0 ) ， ∴直线 l 3 方程为y=− x+1，…………8分 3 x2 + y2 =1,   4 联立方程组 得7x2 −8 3x=0，……9分  3 y =− x+1,   3 8 3 设P(x,y ),Q(x ,y )， 则x +x = ， 1 1 2 2 1 2 7 x x =0,…………………11分 1 2 2 2  3 8 3 16 ∴ PQ = 1+k2 x −x = 1+−    −40 = ，………13分 1 2  3   7  7     点F 到直线 1 P Q 3 ( ) −  − 3 +1−0 3 2 d = = = 3 的距离 ，………14分 2 2 3  3 1+−  3 3   1 1 16 8 3 ∴S = PQ d =   3 = .………15分 △F 1 PQ 2 2 7 7 17. 解：设A =甲答对一道题 ， A =甲答对两道题 ， 1 2 B =乙答对一道题 ， B =乙答对两道题 1 2 3 3 9 （1）①由题P(A )=  = ，………3分 2 4 4 16 3 1 1 3 3 P(A)=  +  = .………5分 1 4 4 4 4 8 {#{QQABLYIAogAgAAJAAQgCQQFQCkAQkgAACQgOwBAEMAIBCRNABAA=}#}4 4 ②同理：由题知P(B )= ，P(B )= ， 1 9 2 9 设 4 A = “甲、乙各两次作答中一共答对3次题”，则 A= AB +A B,AB 与 1 2 2 1 1 2 A 2 B 1 互斥， A 1 与 B 2 , A 2 与 B 1 分别相互独立， 所以P(A)=P(AB )+P(AB )=P(A)P(B )+P(A )P(B ) 1 2 2 1 1 2 2 1 3 4 9 4 5 =  +  = ， 8 9 16 9 12 因此，甲、乙各两次作答中一共答对3次题的概率 1 5 2 ．……8分 （2）由题知：P(A)=2a(1−a),P(A )=a2,P(B )=2b(1−b),P(B )=b2， 1 2 1 2 设 A = “甲、乙各两次作答中一共答对3次题”，则 A= AB +A B,AB 与A B 互斥，A与B ,A 与B 分别相互独立， 1 2 2 1 1 2 2 1 1 2 2 1 所以P(A)=P(AB )+P(AB )=P(A)P(B )+P(A )P(B ) 1 2 2 1 1 2 2 1 =2a(1−a)b2+2b(1−b)a2 =2ab(a+b)−2ab   = 2 ( a b ) 2 ,……12分 a+b=3ab2 ab， 4 2 ab ，当且仅当a=b= 时等号成立，……14分 9 3 32 2(ab)2  ． 81 所以甲、乙各两次作答中一共答对3次题的概率的最小值为 3 8 2 1 .……15分 x2 + y2 =4, 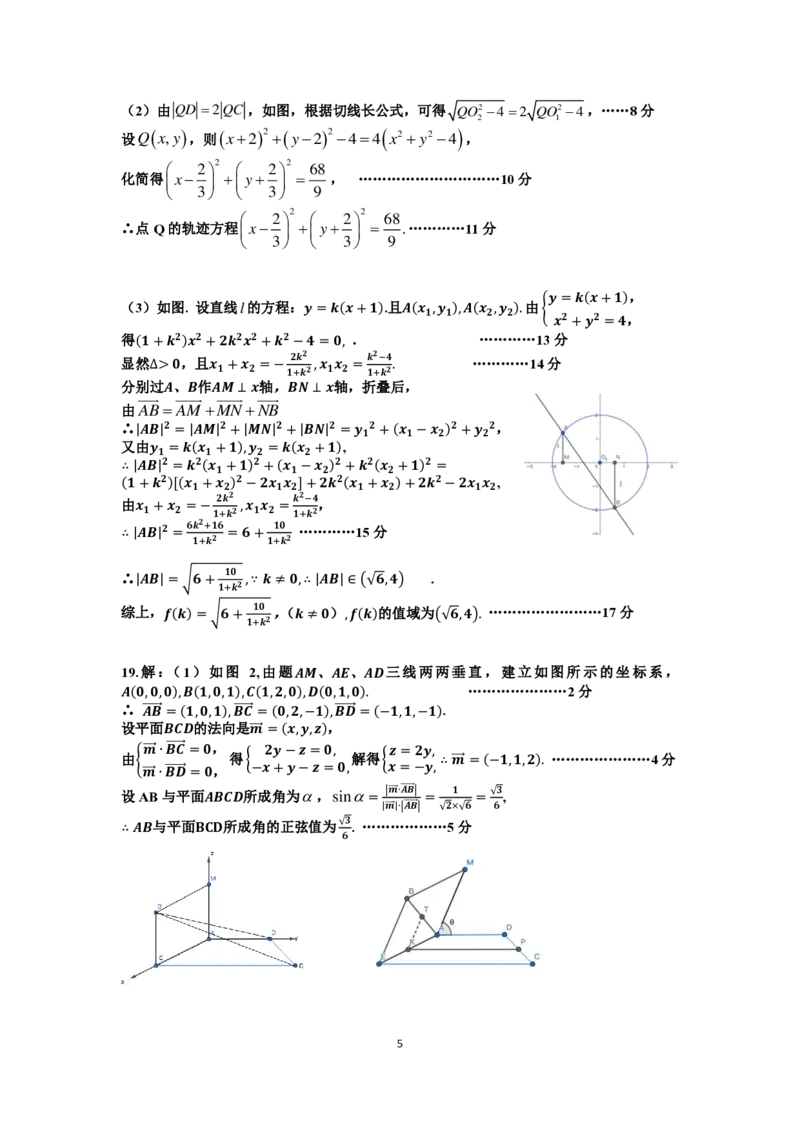18.解：（1）如图所示，由 (x−1)2 +(y−4)2 =9, 两式相减x2 + y2 −[(x−1)2 +(y−4)2]=−5, 化简得x+4y−6=0. 所以圆 O 1 与圆 O 3 的公共弦所在的直线方程为x+4y−6=0. ………………3分 又∵圆𝑶 与圆𝑶 关于直线𝒙+𝒚=𝟐对称，设圆𝑶 的圆心为(𝒂,𝒃)， 𝟏 𝟐 𝟐 𝒃 =−𝟏， 𝒂 𝒂=−𝟐， ∴{ 解得{ 𝒂 𝒃 𝒃=−𝟐. − +𝟐 =𝟎， 𝟐 𝟐 ∴圆𝑶 方程为(𝒙+𝟐)𝟐+(𝒚−𝟐)𝟐 =𝟒. …………………………6分 𝟐 {#{QQABLYIAogAgAAJAAQgCQQFQCkAQkgAACQgOwBAEMAIBCRNABAA=}#}（2）由 5 Q D = 2 Q C ，如图，根据切线长公式，可得 QO2−4 =2 QO2−4，……8分 2 1 设Q(x,y) ，则(x+2)2 +(y−2)2 −4=4 ( x2+ y2−4 ) ， 2 2  2  2 68 化简得  x−  +  y+  = ， …………………………10分  3  3 9 2 2  2  2 68 ∴点Q的轨迹方程  x−  +  y+  = .…………11分  3  3 9 （3）如图. 设直线 l 𝒚=𝒌(𝒙+𝟏)， 的方程：𝒚=𝒌(𝒙+𝟏).且𝑨(𝒙 ,𝒚 ),𝑨(𝒙 ,𝒚 ).由{ 𝟏 𝟏 𝟐 𝟐 𝒙𝟐+𝒚𝟐 =𝟒， 得(𝟏+𝒌𝟐)𝒙𝟐+𝟐𝒌𝟐𝒙𝟐+𝒌𝟐−𝟒 =𝟎, ． …………13分 显然∆>𝟎，且𝒙 +𝒙 =− 𝟐𝒌𝟐 ,𝒙 𝒙 = 𝒌𝟐−𝟒 . …………14分 𝟏 𝟐 𝟏+𝒌𝟐 𝟏 𝟐 𝟏+𝒌𝟐 分别过𝑨、𝑩作𝑨𝑴⊥𝒙轴，𝑩𝑵⊥ 𝒙轴，折叠后， 由AB= AM +MN+NB ∴|𝑨𝑩|𝟐 =|𝑨𝑴|𝟐+|𝑴𝑵|𝟐+|𝑩𝑵|𝟐 =𝒚 𝟐+(𝒙 −𝒙 )𝟐+𝒚 𝟐， 𝟏 𝟏 𝟐 𝟐 又由𝒚 =𝒌(𝒙 +𝟏),𝒚 =𝒌(𝒙 +𝟏), 𝟏 𝟏 𝟐 𝟐 ∴|𝑨𝑩|𝟐 =𝒌𝟐(𝒙 +𝟏)𝟐+(𝒙 −𝒙 )𝟐+𝒌𝟐(𝒙 +𝟏)𝟐 = 𝟏 𝟏 𝟐 𝟐 (𝟏+𝒌𝟐)[(𝒙 +𝒙 )𝟐−𝟐𝒙 𝒙 ]+𝟐𝒌𝟐(𝒙 +𝒙 )+𝟐𝒌𝟐−𝟐𝒙 𝒙 , 𝟏 𝟐 𝟏 𝟐 𝟏 𝟐 𝟏 𝟐 由𝒙 +𝒙 =− 𝟐𝒌𝟐 ,𝒙 𝒙 = 𝒌𝟐−𝟒， 𝟏 𝟐 𝟏+𝒌𝟐 𝟏 𝟐 𝟏+𝒌𝟐 ∴|𝑨𝑩|𝟐 = 𝟔𝒌𝟐+𝟏𝟔 =𝟔+ 𝟏𝟎 …………15分 𝟏+𝒌𝟐 𝟏+𝒌𝟐 ∴|𝑨𝑩|=√𝟔+ 𝟏𝟎 ,∵𝒌≠𝟎,∴|𝑨𝑩|∈(√𝟔,𝟒) . 𝟏+𝒌𝟐 综上，𝒇(𝒌)=√𝟔+ 𝟏𝟎 ，（𝒌≠𝟎）,𝒇(𝒌)的值域为(√𝟔,𝟒). ……………………17分 𝟏+𝒌𝟐 19.解：（1）如图 2,由题𝑨𝑴、𝑨𝑬、𝑨𝑫三线两两垂直，建立如图所示的坐标系， 𝑨(𝟎,𝟎,𝟎),𝑩(𝟏,𝟎,𝟏),𝑪(𝟏,𝟐,𝟎),𝑫(𝟎,𝟏,𝟎). …………………2分 ∴ 𝑨⃗⃗⃗⃗𝑩⃗⃗ =(𝟏,𝟎,𝟏),𝑩⃗⃗⃗⃗⃗𝑪⃗ =(𝟎,𝟐,−𝟏),𝑩⃗⃗⃗⃗𝑫⃗⃗ =(−𝟏,𝟏,−𝟏). 设平面𝑩𝑪𝑫的法向是𝒎⃗⃗⃗ =(𝒙,𝒚,𝒛)， 𝒎⃗⃗⃗ ∙𝑩⃗⃗⃗⃗⃗𝑪⃗ =𝟎， 𝟐𝒚−𝒛=𝟎, 𝒛=𝟐𝒚, 由{ 得{ 解得{ ∴𝒎⃗⃗⃗ =(−𝟏,𝟏,𝟐). …………………4分 𝒎⃗⃗⃗ ∙𝑩⃗⃗⃗⃗𝑫⃗⃗ =𝟎， −𝒙+𝒚−𝒛=𝟎, 𝒙=−𝒚, 设AB与平面𝑨𝑩𝑪𝑫所成角为，  s i n |𝒎⃗⃗⃗ ∙𝑨⃗⃗⃗⃗⃗𝑩⃗ | 𝟏 √𝟑 = = = , |𝒎⃗⃗⃗ |∙|𝑨⃗⃗⃗⃗⃗𝑩⃗ | √𝟐×√𝟔 𝟔 ∴𝑨𝑩与平面𝐁𝐂𝐃所成角的正弦值为√𝟑 . ………………5分 𝟔 {#{QQABLYIAogAgAAJAAQgCQQFQCkAQkgAACQgOwBAEMAIBCRNABAA=}#}（2）如图，设𝑨𝑬、𝑨𝑩的中点分别为𝑲、𝑻，连接𝑲𝑻. 由平面几何知：𝑨𝑬⊥𝑲𝑻、𝑨𝑬⊥𝑷𝑲，∴∠𝑷𝑲𝑻=𝜽，………………7分 且𝑨𝑬⊥平面𝑷𝑲 𝑻.又𝑨𝑬⊂平面𝑨𝑩𝑬 ∴平面PKT 6 ⊥ 平面ABE, 过P 作PQ ⊥ KT于Q, ∴又𝑸∈𝑲𝑻………………………………………………………………9分 在△𝑷𝑲𝑸中，𝐬𝐢𝐧𝜽 = 𝑷𝑸，∵ 𝒑𝒌 =   4 , P K = 3 2 , 3 2 解得PQ = .……………………………………11分 4 说明:若采用建系方法,请老师们根据情况给步骤分. 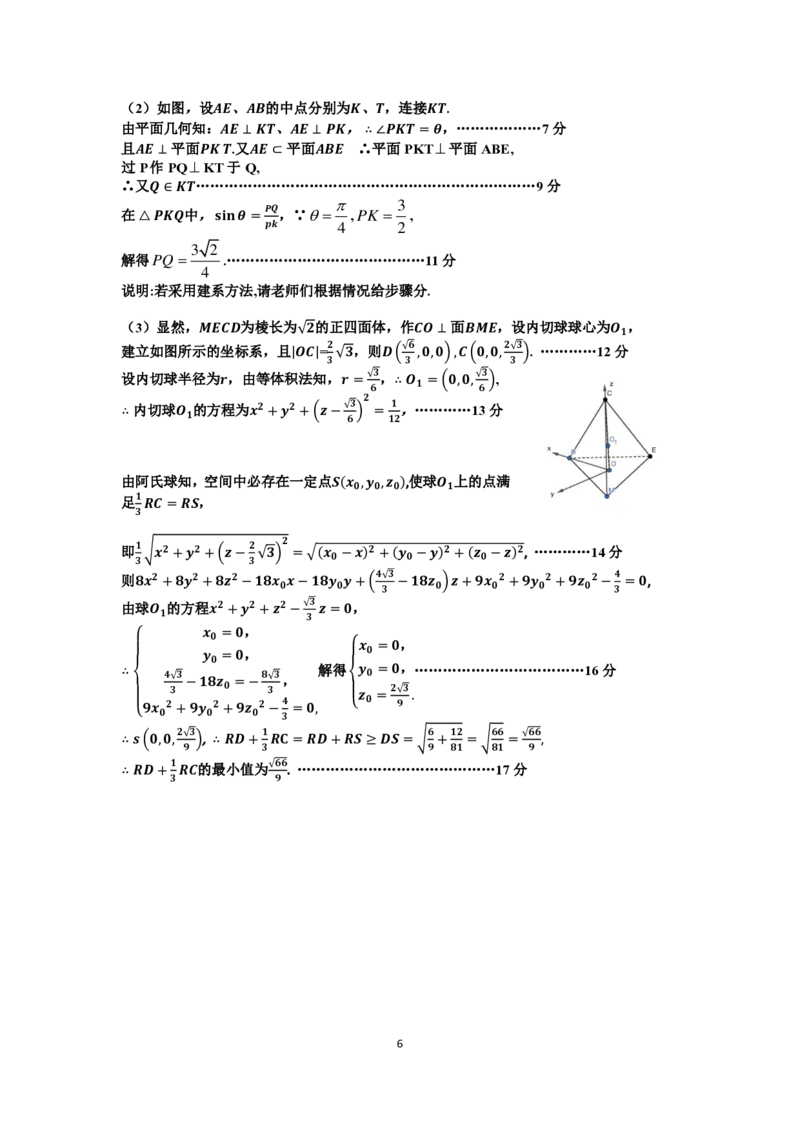（3）显然，𝑴𝑬𝑪𝑫为棱长为√𝟐的正四面体，作𝑪𝑶⊥面𝑩𝑴𝑬，设内切球球心为𝑶 ， 𝟏 建立如图所示的坐标系，且|𝑶𝑪|= 𝟐 √𝟑，则𝑫( √𝟔 ,𝟎,𝟎),𝑪(𝟎,𝟎, 𝟐√𝟑 ). …………12分 𝟑 𝟑 𝟑 设内切球半径为𝒓，由等体积法知，𝒓= √𝟑，∴𝑶 =(𝟎,𝟎, √𝟑 ), 𝟏 𝟔 𝟔 𝟐 ∴内切球𝑶 的方程为𝒙𝟐+𝒚𝟐+(𝒛− √𝟑 ) = 𝟏，…………13分 𝟏 𝟔 𝟏𝟐 由阿氏球知，空间中必存在一定点𝑺(𝒙 ,𝒚 ,𝒛 ),使球𝑶 上的点满 𝟎 𝟎 𝟎 𝟏 足𝟏 𝑹𝑪=𝑹𝑺， 𝟑 𝟐 即𝟏√𝒙𝟐+𝒚𝟐+(𝒛− 𝟐 √𝟑) =√(𝒙 −𝒙)𝟐 +(𝒚 −𝒚)𝟐+(𝒛 −𝒛)𝟐, …………14分 𝟎 𝟎 𝟎 𝟑 𝟑 则𝟖𝒙𝟐+𝟖𝒚𝟐+𝟖𝒛𝟐−𝟏𝟖𝒙 𝒙−𝟏𝟖𝒚 𝒚+( 𝟒√𝟑 −𝟏𝟖𝒛 )𝒛+𝟗𝒙 𝟐+𝟗𝒚 𝟐+𝟗𝒛 𝟐− 𝟒 =𝟎, 𝟎 𝟎 𝟎 𝟎 𝟎 𝟎 𝟑 𝟑 由球𝑶 的方程𝒙𝟐+𝒚𝟐+𝒛𝟐− √𝟑 𝒛=𝟎， 𝟏 𝟑 𝒙 =𝟎， 𝟎 𝒙 =𝟎， 𝒚 𝟎 =𝟎， 𝟎 ∴ 𝟒√𝟑 −𝟏𝟖𝒛 =− 𝟖√𝟑， 解得 𝒚 𝟎 =𝟎，………………………………16分 𝟗𝒙 𝟐 𝟑 +𝟗𝒚 𝟐+ 𝟎 𝟗𝒛 𝟐 𝟑 − 𝟒 =𝟎, { 𝒛 𝟎 = 𝟐√ 𝟗 𝟑 . { 𝟎 𝟎 𝟎 𝟑 𝟐√𝟑 𝟏 𝟔 𝟏𝟐 𝟔𝟔 √𝟔𝟔 ∴𝒔(𝟎,𝟎, ), ∴𝑹𝑫+ 𝑹𝐂=𝑹𝑫+𝑹𝑺≥𝑫𝑺=√ + =√ = , 𝟗 𝟑 𝟗 𝟖𝟏 𝟖𝟏 𝟗 ∴𝑹𝑫+ 𝟏 𝑹𝑪的最小值为√𝟔𝟔 . ……………………………………17分 𝟑 𝟗 {#{QQABLYIAogAgAAJAAQgCQQFQCkAQkgAACQgOwBAEMAIBCRNABAA=}#}