山东省夏津第一中学2024-2025学年下学期第一次月考高二物理试题答案_2024-2025高二（7-7月题库）_2025年04月试卷(1)_0406山东省德州市夏津第一中学2024-2025学年高二下学期第一次月考

物理参考答案 1.B解析 甲图中穿过线圈的磁场方向向下，且磁通量在增大，根据 “增反减同”可知 感应电流产生的磁场方向向上，A错误；乙图磁体正向线圈靠近，穿过线圈的磁通量在 增大，根据 “来拒去留”可知磁体受到线圈作用力的方向向上，B正确；丙图中电流 计指针偏转方向与甲图中相反，说明磁体在远离线圈，C错误；丁图中穿过线圈的磁场 方向向上，且磁通量在减小，根据 “增反减同”可知感应电流产生的磁场方向向上， 与甲图中感应电流产生的磁场方向相同，所以感应电流方向也相同，电流计指针的偏 转方向相同，D错误。 2 .C解析 按下按钮过程，穿过螺线管的磁场向左，磁通量增大，根据楞次定律可知螺 线管中感应电流为从P端流入，从Q端流出，螺线管充当电源，则Q端电势较高，故A 错误；松开按钮过程，穿过螺线管的磁场向左，磁通量减小，根据楞次定律可知螺线 管中感应电流为从Q端流入，从P端流出，螺线管充当电源，则P端电势较高，故B 错误；按住按钮不动，穿过螺线管的磁通量不变，螺线管不会产生感应电动势，故C 正确；按下和松开按钮过程，螺线管中磁通量的变化率不一定相同，故螺线管产生的 感应电动势不一定相同，故D错误。 3.B解析 北极地磁场有竖直向下的分量，由右手定则可知汽车从东向西运动时感应电 动势方向由右指向左，所以左端电势高，故A错误，B正确；由右手定则可知汽车从西 向东运动时感应电动势方向由右指向左，所以左端电势高，故C、D错误。 4.B解析 当圆环运动到题图所示位置时，根据几何关系可知圆环切割磁感线的有效长 度为 R，产生的感应电动势E= BRv，设圆环的总电阻为R ，电路中的电流I= ， 总 总 3 3 圆环处于题图所示位置时，外电路的电阻值R = R ，根据欧姆定律可知U=IR = BRv， 外 总 外 2 2 3 根据右手定则可知，a点的电势高于b点的电势3，则a、b两点的电势差U= B3Rv ab 2 3 5. D解A．将线圈匝数增加一倍时，线圈中的感应电动势增加一倍，但是由于线3圈匝数 的增加还会引起线圈电阻的增加，使电阻也增加了一倍，所以感应电流没有发生变化， A错误；B．将线圈面积增加一倍，感应电动势也增加了一倍，但是还是因为面积的增 加会对线圈的电阻产生影响，导线的长度增加，使电阻也增加为原来的 2 倍，线圈 中的感应电流不是增加一倍，B错误；C．将线圈半径变为原来的一半，面积减小为原 来的四分之一，感应电动势减小为原来的四分之一，电阻减小为原来的二分之一，所 第 1 页 共 6 页 {#{QQABRYCEggCAABBAAQhCAwnACgMQkAGACQoGQBAQsAAAQBFABAA=}#}以感应电流变为原来的二分之一，C错误；D．当线圈平面转到跟磁感线方向垂直时， 线圈的有效面积变为原来的二倍，感应电动势变为原来的二倍，其他条件不变，感应 电流变为原来的二倍，D正确。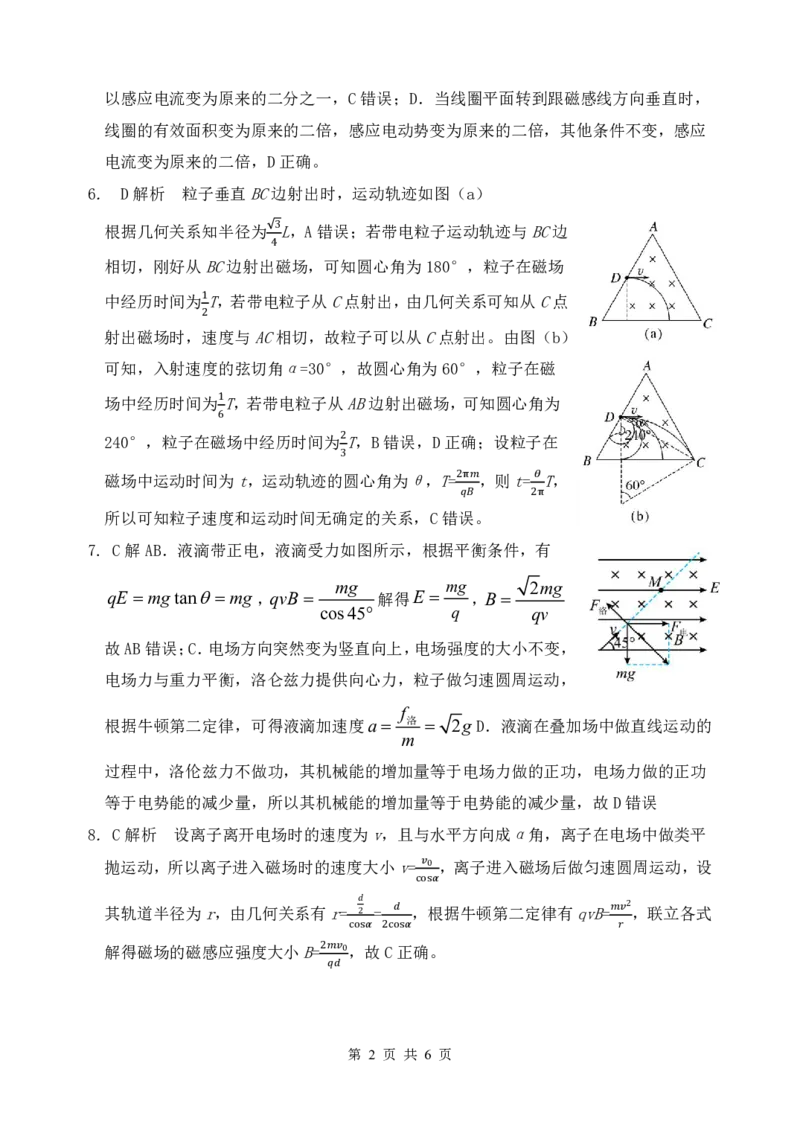 6. D解析 粒子垂直BC边射出时，运动轨迹如图（a） 根据几何关系知半径为 L，A错误；若带电粒子运动轨迹与BC边 3 相切，刚好从BC边射出4磁场，可知圆心角为180°，粒子在磁场 中经历时间为 T，若带电粒子从C点射出，由几何关系可知从C点 1 射出磁场时，速2 度与AC相切，故粒子可以从C点射出。由图（b） 可知，入射速度的弦切角α=30°，故圆心角为60°，粒子在磁 场中经历时间为 T，若带电粒子从AB边射出磁场，可知圆心角为 1 240°，粒子在磁6场中经历时间为 T，B错误，D正确；设粒子在 2 磁场中运动时间为t，运动轨迹的3圆心角为θ，T= ，则t= T， 2π 所以可知粒子速度和运动时间无确定的关系，C错误 。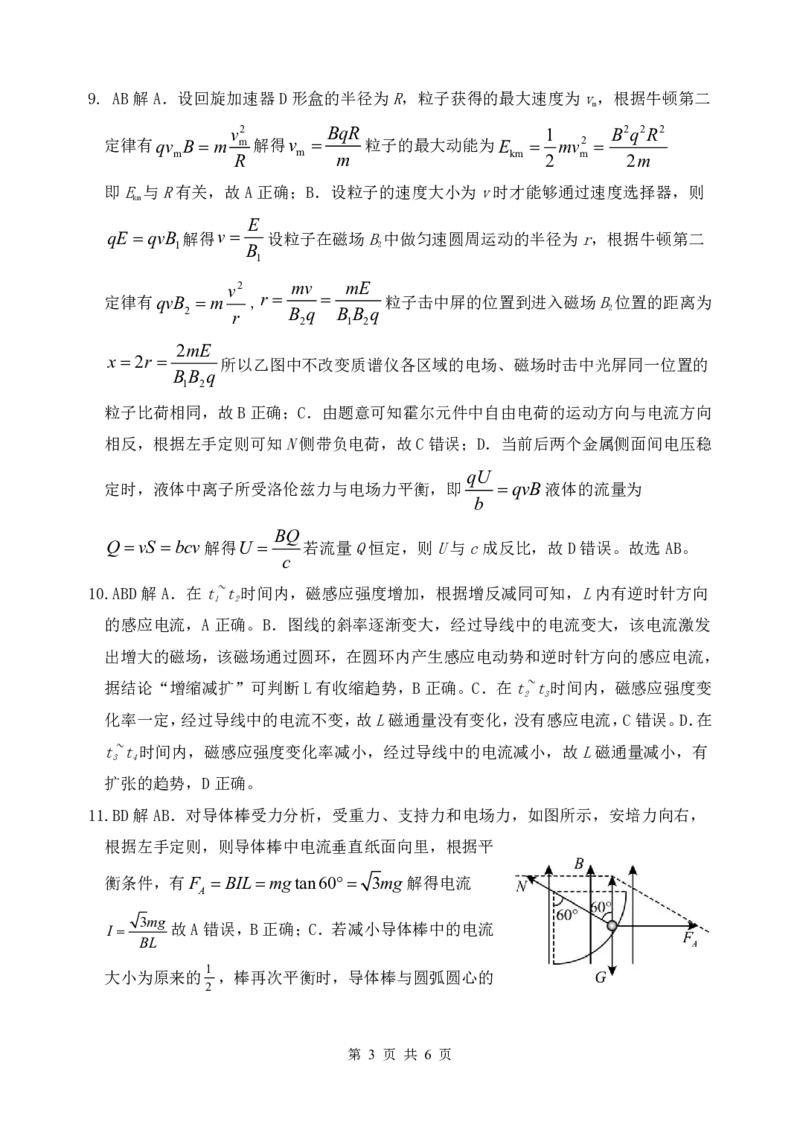 2π 7. 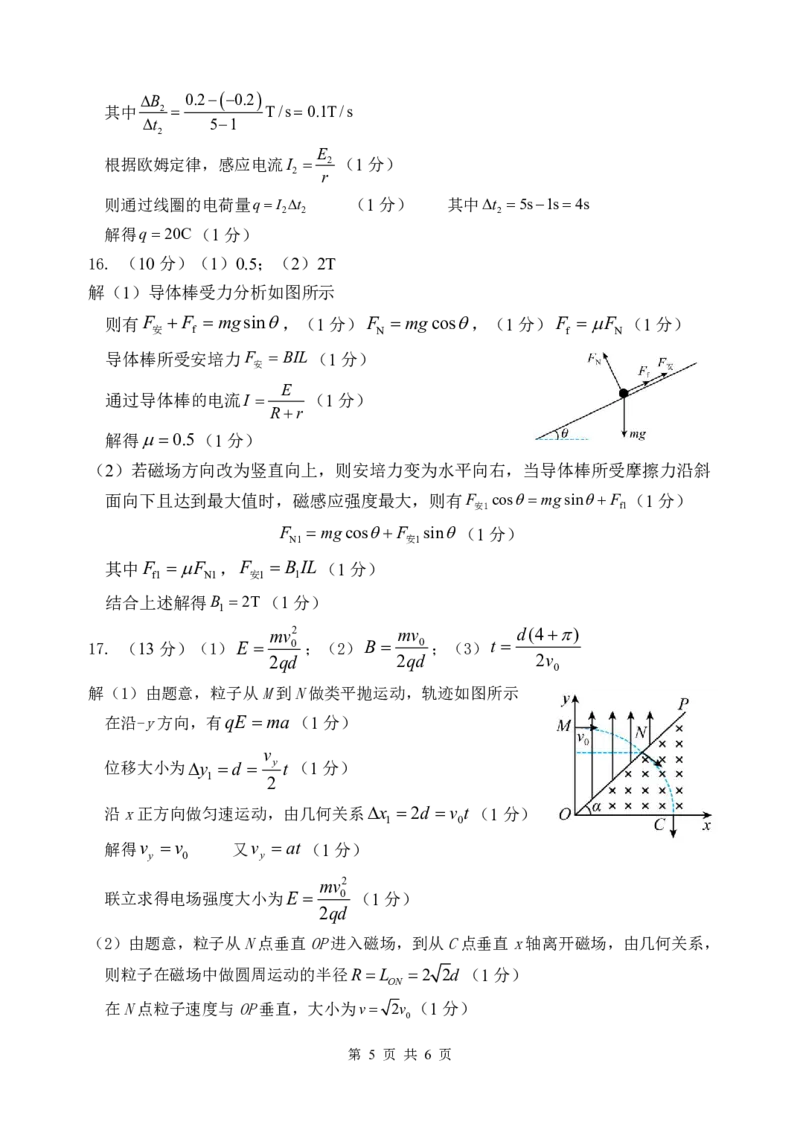C解AB．液滴带正电，液滴受力如图所示，根据平衡条件，有 mg mg 2mg qE mgtanmg，qvB  解得E  ，B  cos45 q qv 故AB错误；C．电场方向突然变为竖直向上，电场强度的大小不变， 电场力与重力平衡，洛仑兹力提供向心力，粒子做匀速圆周运动， f 根据牛顿第二定律，可得液滴加速度a  洛  2gD．液滴在叠加场中做直线运动的 m 过程中，洛伦兹力不做功，其机械能的增加量等于电场力做的正功，电场力做的正功 等于电势能的减少量，所以其机械能的增加量等于电势能的减少量，故D错误 8.C解析 设离子离开电场时的速度为v，且与水平方向成α角，离子在电场中做类平 抛运动，所以离子进入磁场时的速度大小v= ，离子进入磁场后做匀速圆周运动，设 0 cos 其轨道半径为r，由几何关系有r= = ，根据牛顿第二定律有qvB= ，联立各式 2 2 解得磁场的磁感应强度大小B= ，cos故 2Cco正s 确。 2 0 第 2 页 共 6 页 {#{QQABRYCEggCAABBAAQhCAwnACgMQkAGACQoGQBAQsAAAQBFABAA=}#}9. AB解A．设回旋加速器D形盒的半径为R，粒子获得的最大速度为v，根据牛顿第二 m v2 BqR 1 B2q2R2 定律有qv Bm m 解得v  粒子的最大动能为E  mv2  m R m m km 2 m 2m 即E 与R有关，故A正确；B．设粒子的速度大小为v时才能够通过速度选择器，则 km E qE qvB 解得v 设粒子在磁场B中做匀速圆周运动的半径为r，根据牛顿第二 1 B 2 1 v2 mv mE 定律有qvB m ,r   粒子击中屏的位置到进入磁场B位置的距离为 2 r B q BB q 2 2 1 2 2mE x2r  所以乙图中不改变质谱仪各区域的电场、磁场时击中光屏同一位置的 BB q 1 2 粒子比荷相同，故B正确；C．由题意可知霍尔元件中自由电荷的运动方向与电流方向 相反，根据左手定则可知N侧带负电荷，故C错误；D．当前后两个金属侧面间电压稳 qU 定时，液体中离子所受洛伦兹力与电场力平衡，即 qvB液体的流量为 b BQ QvS bcv解得U  若流量Q恒定，则U与c成反比，故D错误。故选AB。 c 10.ABD解A．在t~t时间内，磁感应强度增加，根据增反减同可知，L内有逆时针方向 1 2 的感应电流，A正确。B．图线的斜率逐渐变大，经过导线中的电流变大，该电流激发 出增大的磁场，该磁场通过圆环，在圆环内产生感应电动势和逆时针方向的感应电流， 据结论“增缩减扩”可判断L有收缩趋势，B正确。C．在t~t时间内，磁感应强度变 2 3 化率一定，经过导线中的电流不变，故L磁通量没有变化，没有感应电流，C错误。D．在 t~t时间内，磁感应强度变化率减小，经过导线中的电流减小，故L磁通量减小，有 3 4 扩张的趋势，D正确。 11.BD解AB．对导体棒受力分析，受重力、支持力和电场力，如图所示，安培力向右， 根据左手定则，则导体棒中电流垂直纸面向里，根据平 衡条件，有F BILmgtan60 3mg解得电流 A 3mg I  故A错误，B正确；C．若减小导体棒中的电流 BL 1 大小为原来的 ，棒再次平衡时，导体棒与圆弧圆心的 2 第 3 页 共 6 页 {#{QQABRYCEggCAABBAAQhCAwnACgMQkAGACQoGQBAQsAAAQBFABAA=}#}连线与竖直方向成角，根据平衡条件，则有F B 1 ILmgtan将I  3mg 代入上 A 2 BL 3 式，可得tan 则30，故C错误；D．如适当增大导体棒中的电流，棒再次平 2 衡时，导体棒与圆弧圆心的连线与竖直方向成角，根据平衡条件，则有 mg F  BILmgtan当电流I增大时，角增大，根据N  可知cos减小， A cos 则N增大，故D正确。故选BD。 12.CD解析 导体框转动的前半周内，AO切割磁感线，感应电动势为E= ，圆弧AB 1 2 段内电流方向从A流向B，由题意知AB两端电压为U= E= ，转动的后2半周BO段切 1 2 1 割磁感线，感应电动势为E= ，圆弧AB段内电流方2向从4B流向A，故A、B错误； 2 2 转动的后半周穿过导体框的磁通2 量变化量为ΔΦ= πBL2，电路总电阻为R=2r，则转动 1 2 的后半周内通过导体框某横截面的电荷量为q= = = ，故C正确；从题图所示位 1 2 2 Δ 2π π 置匀速转动一周过程中，外力对导体框做的功等 于产2 生的4 电能，则 （ ） W= ·T= × = ，故D正确。 2 2 2 2 4 2 2π π 13.（2 8分）（2 1）ABC （42 ）①逆 ②向上 感应电流的磁场总是阻碍引起感应电流的磁场的磁通量的变化 Uneh 14．（6分）（1） 后表面 （2）电压表示数U，电流表示数I I 15.（8分） (1)50V，感应电流方向为abcd a或者顺时针(2)20C  解（1）3s时感应电动势E N 1 （1分） 1 t 1 磁通量的变化量 BS 1 1 B 0.2 根据图乙可知，3s时磁感应强度的变化率大小 1  T/s0.1T/s（1分） t 31 1 代入数据解得E 50V（1分） 1 根据楞次定律可知，感应电流方向为abcd a或者顺时针（1分）  B S （2）在15s内线圈中感应电动势E N 2 N 2 （1分） 2 t t 2 2 第 4 页 共 6 页 {#{QQABRYCEggCAABBAAQhCAwnACgMQkAGACQoGQBAQsAAAQBFABAA=}#}B 0.20.2 其中 2  T/s 0.1T/s t 51 2 E 根据欧姆定律，感应电流I  2 （1分） 2 r 则通过线圈的电荷量qI t （1分） 其中t 5s1s4s 2 2 2 解得q20C（1分） 16. （10分）（1）0.5；（2）2T 解（1）导体棒受力分析如图所示 则有F F mgsin，（1分）F mgcos，（1分）F F （1分） 安 f N f N 导体棒所受安培力F  BIL（1分） 安 E 通过导体棒的电流I  （1分） Rr 解得0.5（1分） （2）若磁场方向改为竖直向上，则安培力变为水平向右，当导体棒所受摩擦力沿斜 面向下且达到最大值时，磁感应强度最大，则有F cosmgsinF （1分） 安1 f1 F mgcosF sin（1分） N1 安1 其中F F ，F  BIL（1分） f1 N1 安1 1 结合上述解得B 2T（1分） 1 mv2 mv d(4) 17. （13分）（1）E  0 ；（2）B  0 ；（3）t  2qd 2qd 2v 0 解（1）由题意，粒子从M到N做类平抛运动，轨迹如图所示 在沿-y方向，有qE ma（1分） v 位移大小为y d  y t（1分） 1 2 沿x正方向做匀速运动，由几何关系x 2d v t（1分） 1 0 解得v v 又v at（1分） y 0 y mv2 联立求得电场强度大小为E  0 （1分） 2qd （2）由题意，粒子从N点垂直OP进入磁场，到从C点垂直x轴离开磁场，由几何关系， 则粒子在磁场中做圆周运动的半径RL 2 2d（1分） ON 在N点粒子速度与OP垂直，大小为v 2v （1分） 0 第 5 页 共 6 页 {#{QQABRYCEggCAABBAAQhCAwnACgMQkAGACQoGQBAQsAAAQBFABAA=}#}v2 由牛顿第二定律qvBm （1分） R mv 解得B 0 （1分） 2qd 2d （3）由运动规律，粒子在电场中做类平抛的时间为t ，有t  （1分） 1 1 v 0 1 2R 粒子在磁场中做匀速圆周运动的时间为t 2 ，有t 2 = ， t  8  R （1分） 1 2 2v 4 2v 0 0 8 d(4) 故从M点运动到C点所用的总时间为t t t  （2分） 1 2 2v 0 18.（15分） （1）0.4 A 顺时针 （2）2.5 s （3）①1 C ②12.8N 解（1）根据法拉第电磁感应定律E= = （1分） Δ 1|Δ 解得E=2.4V Δ Δ 由闭合电路欧姆定律得I= =0.4A（1分） 由楞次定律可知，电流方向 +为 顺时针方向；（1分） （2）金属棒对竖直挡杆的挤压恰好消失，则BIL=μmg（2分） 1 又由B=（2-0.4t）T得t=2.5s（1分） 1 1 1 （3）①由电流的定义式可得Q=IΔt（1分） 由闭合电路欧姆定律得I= （1分） 由法拉第电磁感应定律得E += = （1分） Δ 1 2 则Q= =1C（1分） Δ Δ 1 2 ②撤去竖 直+ 挡杆施加外力F后，金属棒做a=5m/s2的匀加速直线运动， B=1T，v=a（t-t）=5（t-2.5）（1分） 1 1 由牛顿第二定律可得F-μmg-F=ma（1分） A F=BiL，i= （1分） A 1 1 则F=2.8+ （ + ） （N）（1分） 10 −2.5 当t=t=5.5s时3 v=15m/s，F=12.8N （1分） 2 第 6 页 共 6 页 {#{QQABRYCEggCAABBAAQhCAwnACgMQkAGACQoGQBAQsAAAQBFABAA=}#}