文档内容
64 级高二上学期第一次阶段性检测
数学试题
一、单选题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
1. 已知点 关于 轴的对称点为 ,则 等于( )
A. B. C. 2 D.
2. 直线 的一个方向向量为( )
A. B. (−3,2) C. (2,3) D.
3. 在空间四边形ABCD中,E,F分别为BC,CD的中点,则 ( )
A. B. C. D.
4. 已知点 , , ,若A,B,C三点共线,则a,b的值分别是( )
A. ,3 B. ,2 C. 1,3 D. ,2
5. “ ”是“直线 与直线 垂直”的( )
.
A 充要条件 B. 必要不充分条件
C. 充分不必要条件 D. 既不充分也不必要条件
的
6. 在所有棱长均为2 平行六面体 中, ,则 的
长为( )
A. B. C. D. 6
7. 数学家欧拉于1765年在他的著作《三角形的几何学》中首次提出定理:三角形的外心、重心、垂心依
次位于同一直线上,且重心到外心的距离是重心到垂心距离的一半,这条直线被后人称之为三角形的欧拉
线.已知 的顶点为 , , ,则该三角形的欧拉线方程为( )A. B.
.
C D.
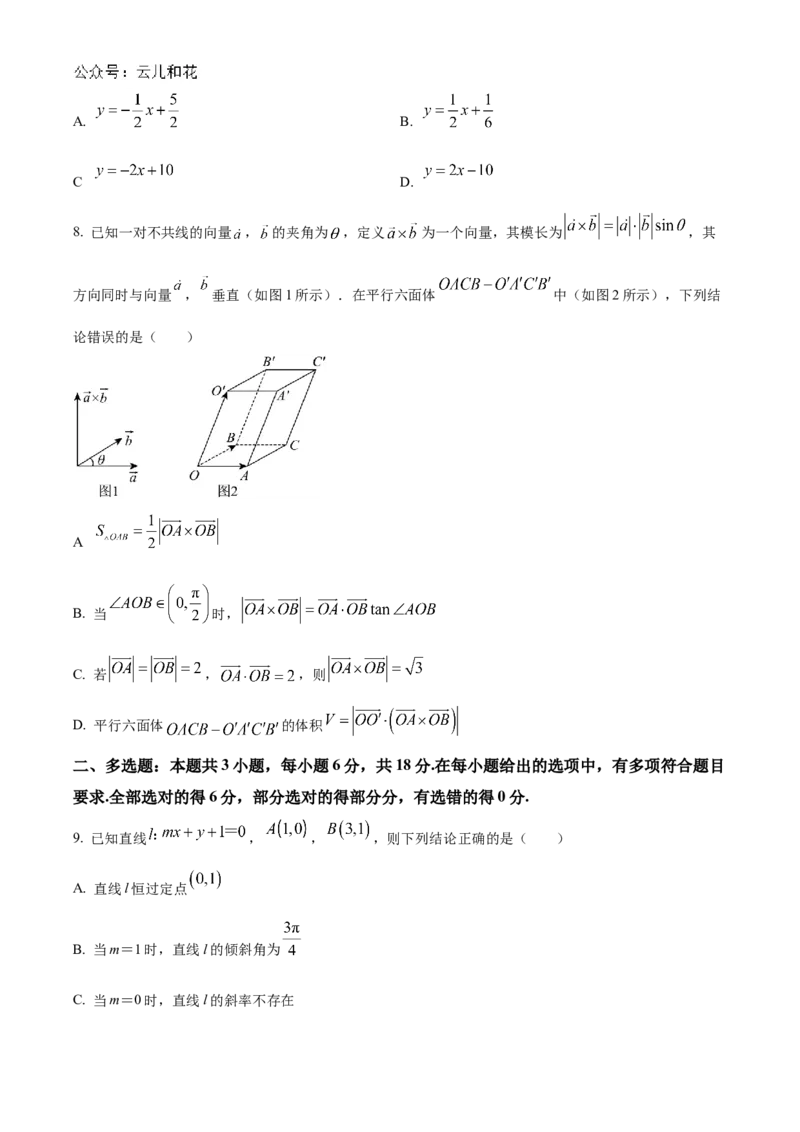
8. 已知一对不共线的向量 , 的夹角为 ,定义 为一个向量,其模长为 ,其
方向同时与向量 , 垂直(如图1所示).在平行六面体 中(如图2所示),下列结
论错误的是( )
.
A
B. 当 时,
C. 若 , ,则
D. 平行六面体 的体积
二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目
要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9. 已知直线 , , ,则下列结论正确的是( )
A. 直线l恒过定点
B. 当m=1时,直线l的倾斜角为
C. 当m=0时,直线l的斜率不存在D. 当m=2时,直线l与直线AB垂直
10. 已知向量 ,则下列结论正确的是( )
A. 若 ,则 B. 若 ,则
C. 的最小值为 D. 的最大值为4
11. 已知四面体 满足 , ,则( )
A. 直线 与 所成的角为
B. 直线 与 所成的角为
C. 点 为直线 上的动点, 到 距离的最小值为
D. 二面角 平面角的余弦值为
三、填空题:本题共3小题,每小题5分,共15分.
12. 在正方体 中,点E是上底面 的中心,若 ,则实数
________.
13. 已知 ,设直线 : , : ,若 ,则 ______.
14. 在如图所示的试验装置中,两个正方形框架ABCD,ABEF的边长都是1,且它们所在的平面互相垂直.
活动弹子M,N分别在正方形对角线AC和BF 上移动,且CM和BN 的长度保持相等,记
,当MN的长最小时,平面MNA与平面MNB夹角的正弦值为_______.四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15. 菱形 的顶点 的坐标分别为 边所在直线过点 .
(1)求 边所在直线的方程;
(2)求对角线 所在直线的方程.
的
16. 如图,在正四棱柱 中, , , , 分别为 , 中点.
(1)证明: 平面 .
(2)求 与平面 所成角的正弦值.
17. 已知直线 .
(1)求证:直线 经过一个定点;
(2)若直线 交 轴的正半轴于点 ,交 轴的正半轴于点 , 为坐标原点,设 的面积为 ,
求 的最小值及此时直线 的方程.
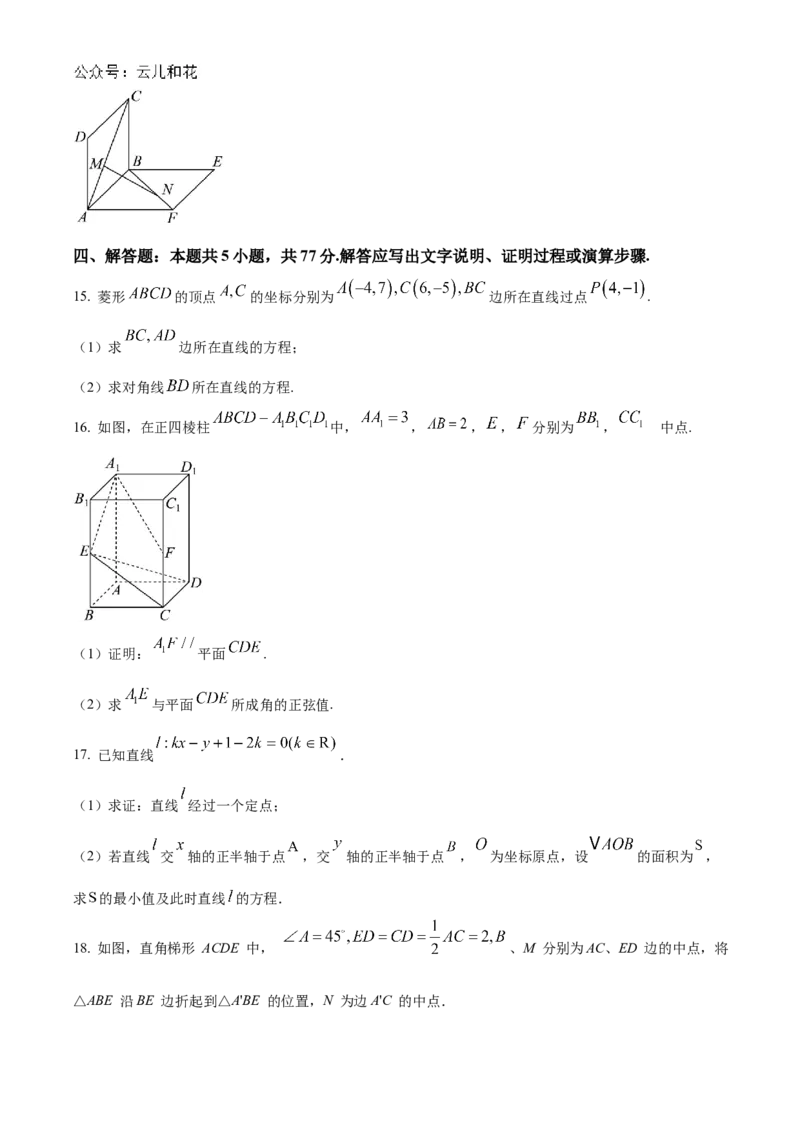
18. 如图,直角梯形 ACDE 中, 、M 分别为AC、ED 边的中点,将
△ABE 沿BE 边折起到△A'BE 的位置,N 为边A'C 的中点.(1)证明:MN∥平面A'BE;
(2)当三棱锥 的体积为 ,且二面角 为锐二面角时,求平面 NBM 与平面
BEDC 夹角的正切值.
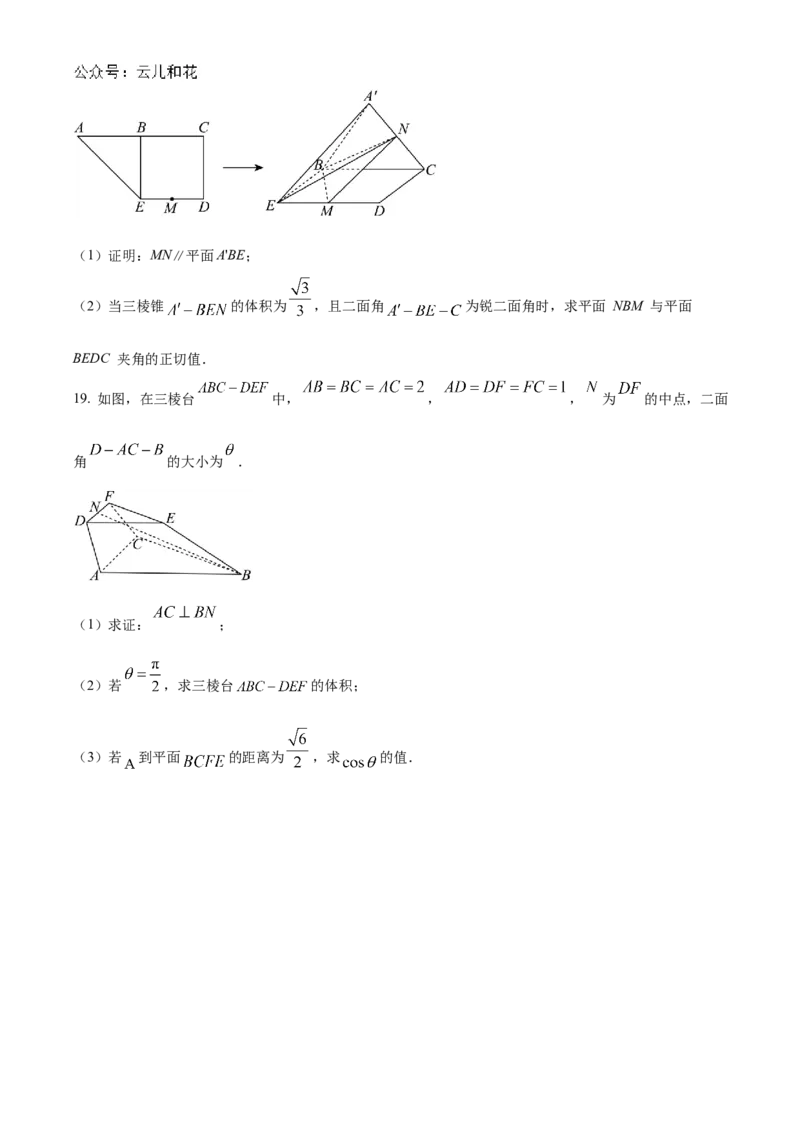
19. 如图,在三棱台 中, , , 为 的中点,二面
角 的大小为 .
(1)求证: ;
(2)若 ,求三棱台 的体积;
(3)若 到平面 的距离为 ,求 的值.64 级高二上学期第一次阶段性检测
数学试题
一、单选题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
【1题答案】
【答案】D
【2题答案】
【答案】B
【3题答案】
【答案】C
【4题答案】
【答案】D
【5题答案】
【答案】C
【6题答案】
【答案】C
【7题答案】
【答案】A
【8题答案】
【答案】C
二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目
要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
【9题答案】
【答案】BD
【10题答案】
【答案】AC
【11题答案】
【答案】BCD
三、填空题:本题共3小题,每小题5分,共15分.
【12题答案】【答案】2
【13题答案】
【答案】1
【14题答案】
【答案】
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
【15题答案】
【答案】(1)BC所在直线方程为 ,AD所在直线方程为
(2)
【16题答案】
【答案】(1)证明见解析
(2)
【17题答案】
【答案】(1)证明见解析;
(2) , .
【18题答案】
【答案】(1)证明见解析
(2)
【19题答案】
【答案】(1)证明见解析;
(2)
(3)