文档内容
公众号:高中试卷君
吉林地区普通高中 2023—2024 学年度高三年级第三次模拟考试
数学试题
说明:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上,贴好条形码.
2.答选择题时,选出每小题答案后,用2B铅笔把答题卡对应题目的答案标号涂黑.如需改动,
用橡皮擦干净后,再选涂其他答案标号.答非选择题时,用0.5毫米的黑色签字笔将答素写在
答题卡上.字体工整,笔迹清楚.
3.请按题号顺序在答题卡相应区域作答,超出区域所写答案无效:在试卷上、草纸上答题无
效.
4.考试结束后,将本试卷和答题卡一并交回.
一、单项选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只
有一个是符合题目要求.
1. 复数 在复平面内对应的点位于( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
【答案】A
【解析】
【分析】由复数几何意义及三角函数值符号判断其所在象限即可.
【详解】由复数的几何意义知,复数 在复平面中对应点 ,
又因为 ,所以 , ,
所以点 位于第一象限.
故选:A.
2. 已知 若 ,则实数 的值为( )
A. 1 B. 4 C. 1或4 D. 2
【答案】B
【解析】
【分析】分 和 ,求解 ,即可得出答案.
第1页/共29页
学科网(北京)股份有限公司公众号:高中试卷君
【详解】当 时, ,则 ,解得: (舍去);
当 时, ,则 ,解得: .
.
故选:B
3. 已知随机变量 ,且 ,则 ( )
A. 0.2 B. 0.3 C. 0.7 D. 0.8
【答案】D
【解析】
【分析】根据正态分布性质可得
【详解】因为 ,所以 ,
所以 .
故选:D.
4. 若互不相等的正数 满足 ,则( )
A. 成等差数列 B. 成等比数列
C. 成等差数列 D. 成等比数列
【答案】D
【解析】
【分析】根据 互不相等,且 得到 ,转化为 ,根据等比中项的概
念,判断 成等比数列.
【详解】因为 互不相等,且 ,所以 ,即 ,
所以 成等比数列.
故选:D
5. 下列函数中,既是奇函数,又在区间 上单调递增的是( )
第2页/共29页
学科网(北京)股份有限公司公众号:高中试卷君
A. B. C. D.
【答案】C
【解析】
【分析】利用奇函数的定义 ,即可判断四个选项的奇偶性,只有 是奇函数,又正切
函数在 上不是单调递增函数,而函数 的导函数恒大于零,所以只有C正确.
【详解】对于A, , 为偶函数,故A错误;
对于B, , 为奇函数,又 在 不满足单
调递增定义,所以B错误;
对于C, , 为奇函数, ,
在区间 上单调递增,故C正确;
对于D, 是非奇非偶函数,所以D错误.
故选:C.
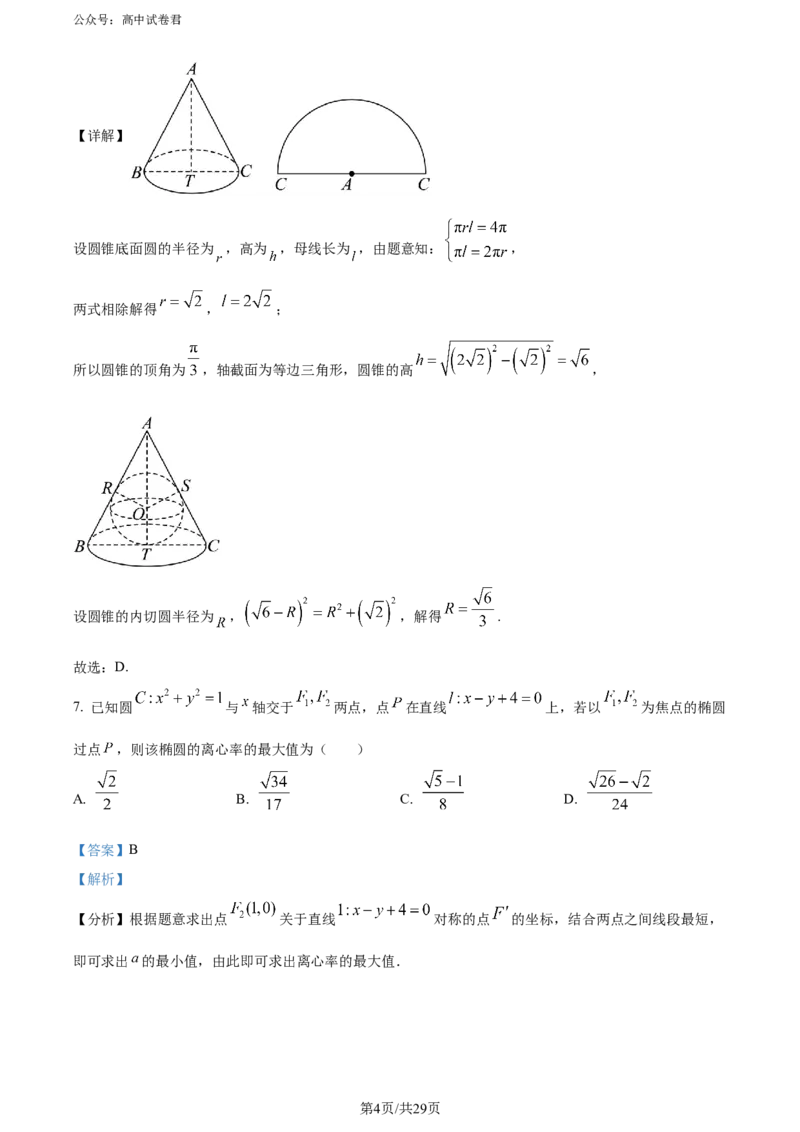
6. 已知圆锥的侧面积是 ,且它的侧面展开图是一个半圆,则这个圆锥的内切球半径为( )
A. B. C. D.
【答案】D
【解析】
【分析】设出圆锥底面圆的半径,并由题意联立方程组求出;再由勾股定理解出圆锥内切球的半径即可.
第3页/共29页
学科网(北京)股份有限公司公众号:高中试卷君
【详解】
设圆锥底面圆的半径为 ,高为 ,母线长为 ,由题意知: ,
两式相除解得 , ;
所以圆锥的顶角为 ,轴截面为等边三角形,圆锥的高 ,
设圆锥的内切圆半径为 , ,解得 .
故选:D.
7. 已知圆 与 轴交于 两点,点 在直线 上,若以 为焦点的椭圆
过点 ,则该椭圆的离心率的最大值为( )
A. B. C. D.
【答案】B
【解析】
【分析】根据题意求出点 关于直线 对称的点 的坐标,结合两点之间线段最短,
即可求出 的最小值,由此即可求出离心率的最大值.
第4页/共29页
学科网(北京)股份有限公司公众号:高中试卷君
【详解】
由题意知 , ,以 , 为焦点的椭圆的半焦距为 ,
由题意可知直线1与椭圆有交点 ,设点 关于直线 对称的点为 ,
则 ,解得 ,
则 ,
因为 ,
则该椭圆的离心率的最大值为 .
故选:B.
8. 已知 为锐角,且 ,则 的最大值为( )
A. B. C. D.
【答案】A
【解析】
【分析】先结合和差角公式及同角基本关系进行化简,然后结合基本不等式即可求解.
【详解】因为 , 为锐角,且 ,
第5页/共29页
学科网(北京)股份有限公司公众号:高中试卷君
两边同时除以 得, ,
,
为锐角, ,
,
当且仅当 ,即 时取等号,
最大值为 .
故选:A.
二、多项选择题:本大题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有
多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9. 已知集合 ,则( )
A. B.
C. D. 的子集个数为2
【答案】BCD
【解析】
【分析】解对数不等式及绝对值不等式,结合集合的交集、并集运算及子集的定义计算即可.
【
详解】对于A项,由题意知, , ,故A项错误;
对于B项, ,故B项正确;
对于C项, ,故C项正确;
对于D项,因为 ,所以 的子集为 、 共2个,故D项正确.
故选:BCD.
第6页/共29页
学科网(北京)股份有限公司公众号:高中试卷君
10. 在 的展开式中,下列说法正确的是( )
A. 各二项式系数的和为64 B. 各项系数的绝对值的和为729
C. 有理项有3项 D. 常数项是第4项
【答案】AB
【解析】
【分析】利用各二项系数和可判断A选项;根据二项式 展开式的系数的绝对值和与二项式
的展开式的系数和相等,可判断B选项;根据展开式的通项可判断C选项和D选项;
【详解】在 的展开式中,各二项式系数的和为 ,故A正确;
各项系数的绝对值的和与 的各项系数和相等,
令 ,可得各项系数的绝对值的和为 ,故B正确;
展开式的通项为 ,
令 ,得 时,展开式的项为有理项,
所以有理项有4项,故C错误;
令 ,得 ,所以常数项是第5项,故D错误.
故选:AB.
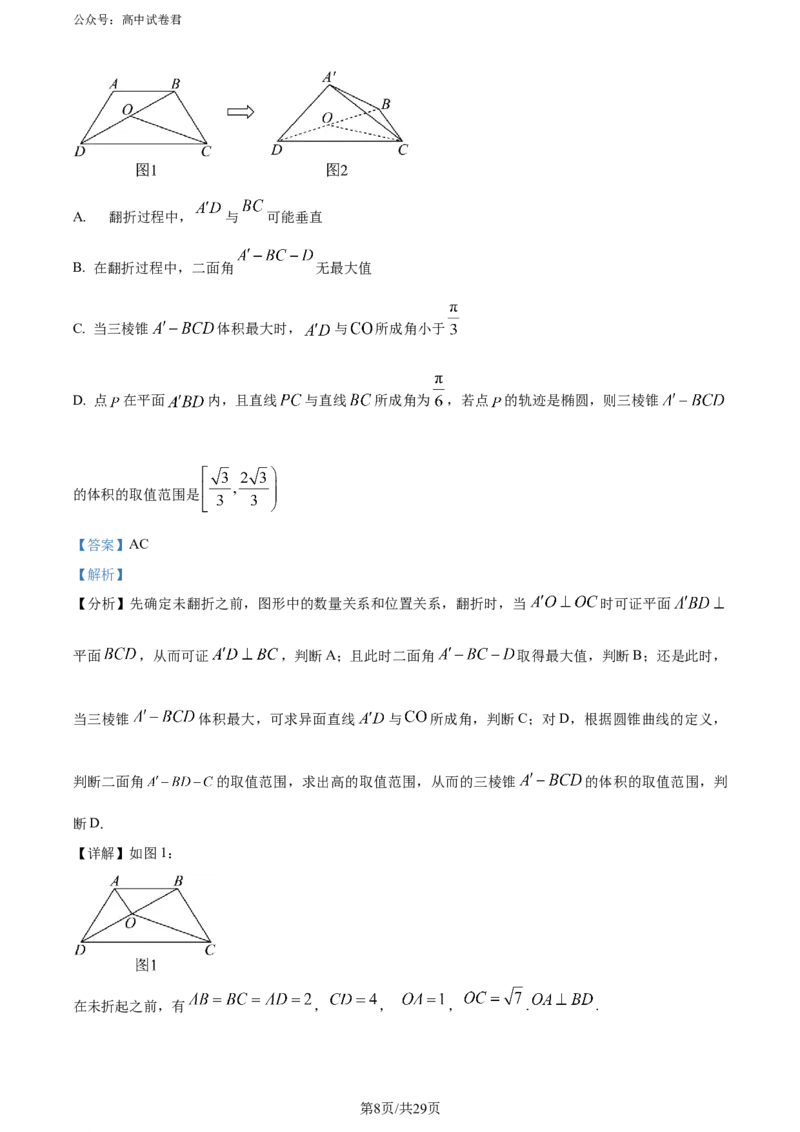
11. 如图1,在等腰梯形 中, ,且 为 的中点,沿 将
翻折,使得点 到达 的位置,构成三棱锥 (如图2),则( )
第7页/共29页
学科网(北京)股份有限公司公众号:高中试卷君
在
A. 翻折过程中, 与 可能垂直
B. 在翻折过程中,二面角 无最大值
C. 当三棱锥 体积最大时, 与 所成角小于
D. 点 在平面 内,且直线 与直线 所成角为 ,若点 的轨迹是椭圆,则三棱锥
的体积的取值范围是
【答案】AC
【解析】
【分析】先确定未翻折之前,图形中的数量关系和位置关系,翻折时,当 时可证平面
平面 ,从而可证 ,判断A;且此时二面角 取得最大值,判断B;还是此时,
当三棱锥 体积最大,可求异面直线 与 所成角,判断C;对D,根据圆锥曲线的定义,
判断二面角 的取值范围,求出高的取值范围,从而的三棱锥 的体积的取值范围,判
断D.
【详解】如图1:
在未折起之前,有 , , , . .
第8页/共29页
学科网(北京)股份有限公司公众号:高中试卷君
又 , ,所以 .
沿 将 翻折,则 点轨迹为一个圆,且圆面一直和 垂直,如图:
当 时, ,又 , 平面 ,
所以 平面 , 平面 ,所以平面 平面 ,
又 平面 ,平面 平面 , ,所以 平面 .
平面 ,所以 .故A正确.
此时 , ,所以 即为二面角 的平面角为 ,是二面角
的最大值,故B错误;
此时三棱锥 的高等于 ,高取得最大值,又底面 不变,所以三棱锥 的体积
最大.
如图:
取 中点 ,连接 , ,则 即为一面直线 与 所成角,
在 中, , , ,
所以 ,
第9页/共29页
学科网(北京)股份有限公司公众号:高中试卷君
所以 ,故C正确;
对D:点 在平面 内,且直线 与直线 所成角为 ,若点 的轨迹是椭圆,根据圆锥曲线的
概念,二面角 应该在 之间取值,且不能为 (此时点 的轨迹是圆),
当二面角 或 时, ,
当二面角 时, ,
所以点 在平面 内,且直线 与直线 所成角为 ,且点 的轨迹是椭圆时,
,故D错误.
故选:AC
【点睛】关键点点睛:用一个平面截圆锥体,要想得到的截面是一个椭圆,截面不能和圆锥的母线相交,
且截面不能与圆锥的轴垂直(此时的截面是圆).
三、填空题:本大題共3小题,每小題5分,共15分.其中第13题的第一个空填对得2分,
第二个空填对得3分.
12. 已知向量 ,若 ,则 _________.
【答案】
【解析】
【分析】根据平面向量数量积的坐标运算得 的值,从而可求模长.
【详解】因为 , ,所以 ,解得 ,
所以 .
第10页/共29页
学科网(北京)股份有限公司公众号:高中试卷君
故答案为: .
13. “冰天雪地也是金山银山”,2023-2024年雪季,东北各地冰雪旅游呈现出一片欣欣向荣的景象,为东北
经济发展增添了新动能.某市以“冰雪童话”为主题打造—圆形“梦幻冰雪大世界”,其中共设“森林姑娘”“扣
像墙”“古堡滑梯”等16处打卡景观.若这16处景观分别用 表示,某游客按照箭头所示方向
(不可逆行)可以任意选择一条路径走向其它景观,并且每个景观至多经过一次,那么他从入口出发,按
图中所示方向到达 有_________种不同的打卡路线;若该游客按上述规则从入口出发到达景观 的不同
路线有 条,其中 ,记 ,则 _________(结果用 表
示).
【答案】 ①. 8 ②.
【解析】
【分析】结合题意及分类加法原理,依次计算到达 、 、 、 、 的走法即可.由题意可知数列
为斐波那契数列,即 ( 且 ),结合累加法求解即可.
【详解】由题意知,到达 点共有1种走法,
到达 点共有 种走法(一种是经过 点到达 ,一种是直接到达 ),
到达 点共有 种走法(一种是经过 ,一种是经过 ,所以到达 将 、 的走法加起来),
第11页/共29页
学科网(北京)股份有限公司公众号:高中试卷君
到达 点共有 种走法(一种是经过 和 ,一种是经过 ,所以到达 将 、 的走法加
起来),
到达 点共有 种走法(一种是经过 和 ,一种是经过 和 ,所以到达 将 、 的
走法加起来),
故按图中所示方向到达 有8种不同的打卡路线.
由题意知, , , , , ,…,
( 且 ),
因为 ( 且 ),
所以 , , ,…, ,( 且 ),
将上式累加可得 ,( 且
),
整理可得 ,又 , ,
所以 ,即 .
故答案为:8; .
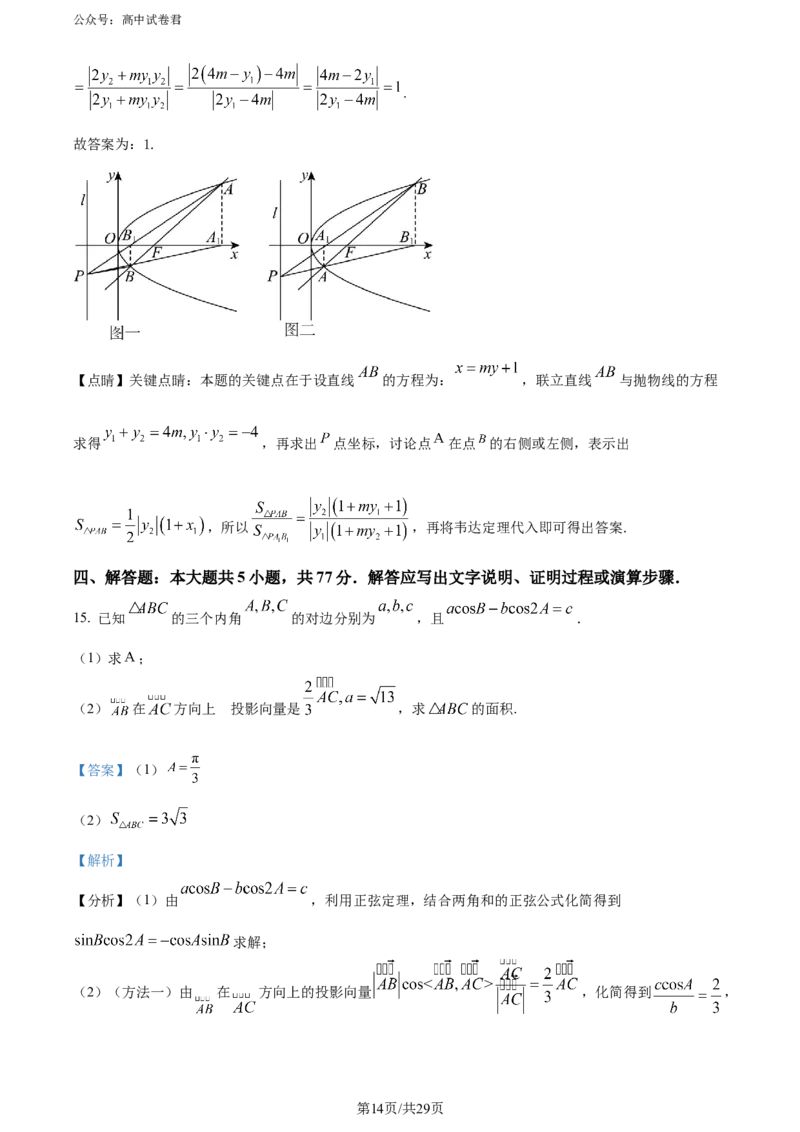
14. 已知拋物线 的焦点为 ,准线为 ,过点 的直线与抛物线 交于 两点,过 作
轴垂线,垂足分別为 ,直线 与直线 交于 点,则 与 的面积比值为_________.
【答案】1
【解析】
【分析】设直线 的方程为: ,联立直线 与抛物线的方程求得 ,
第12页/共29页
学科网(北京)股份有限公司公众号:高中试卷君
再求出 点坐标,讨论点 在点 的右侧或左侧,表示出 ,所以
,再将韦达定理代入即可得出答案.
【详解】依题意作示意图如下图,图一为点 在点 的右侧,图二为点 在点 的左侧,
根据抛物线方程有: ,
设直线 的方程为: , , ,
故 ,若 ,则直线 与直线 不相交,故 ,
联立直线 与抛物线的方程有: ,
则 ,则 ,
直线 的方程为: ,令 ,得到 ,
所以 ,因为 ,
所以 ,
而对于 ,当点 在点 的右侧,根据图象可知,
,
当点 在点 的左侧,根据图象可知,
,
即 ,所以 ,
第13页/共29页
学科网(北京)股份有限公司公众号:高中试卷君
.
故答案为:1.
【点睛】关键点睛:本题的关键点在于设直线 的方程为: ,联立直线 与抛物线的方程
求得 ,再求出 点坐标,讨论点 在点 的右侧或左侧,表示出
,所以 ,再将韦达定理代入即可得出答案.
四、解答题:本大题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15. 已知 的三个内角 的对边分别为 ,且 .
(1)求 ;
(2) 在 方向上 投的影向量是 ,求 的面积.
【答案】(1)
(2)
【解析】
【分析】(1)由 ,利用正弦定理,结合两角和的正弦公式化简得到
求解;
(2)(方法一)由 在 方向上的投影向量 ,化简得到 ,
第14页/共29页
学科网(北京)股份有限公司公众号:高中试卷君
再利用余弦定理求得 即可;(方法二):过 作 ,设 ,在Rt 中,由
求解.
【小问1详解】
解:由正弦定理得 ,
,
即 ,
又 ,
,
即
得 或 (舍),
又 .
【小问2详解】
(方法一) 在 方向上的投影向量为 ,
即 ,
,
由余弦定理 ,
,
,
第15页/共29页
学科网(北京)股份有限公司公众号:高中试卷君
则 ;
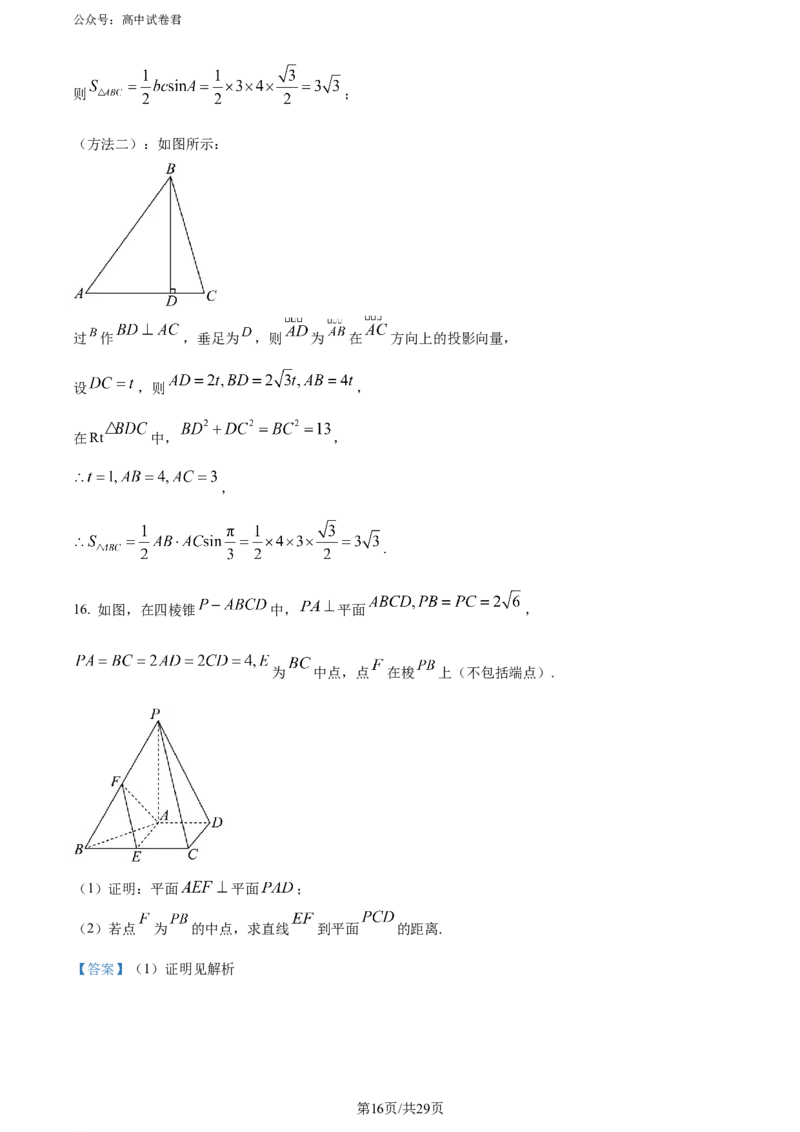
(方法二):如图所示:
过 作 ,垂足为 ,则 为 在 方向上的投影向量,
设 ,则 ,
在Rt 中, ,
,
.
16. 如图,在四棱锥 中, 平面 ,
为 中点,点 在梭 上(不包括端点).
(1)证明:平面 平面 ;
(2)若点 为 的中点,求直线 到平面 的距离.
【答案】(1)证明见解析
第16页/共29页
学科网(北京)股份有限公司公众号:高中试卷君
(2)
【解析】
【分析】(1)由线面垂直的性质与勾股定理,结合三线合一证得 , ,再线面垂直与
面面垂直的判定定理即得证.
(2)由线面平行判定定理可证得 平面 ,则点 到平面 的距离即为 到平面 的距
离.方法一:以 为原点建立空间直角坐标系,运用点到面的距离公式计算即可.方法二:运用等体积法
计算即可.
【小问1详解】
证明:连接 ,如图所示,
平面 ,
,
,即 ,
又 为 中点,则 ,且 ,
四边形 为正方形, ,
平面 平面 ,
又 , 、 平面 , 平面 ,
又 平面 平面 平面 .
第17页/共29页
学科网(北京)股份有限公司公众号:高中试卷君
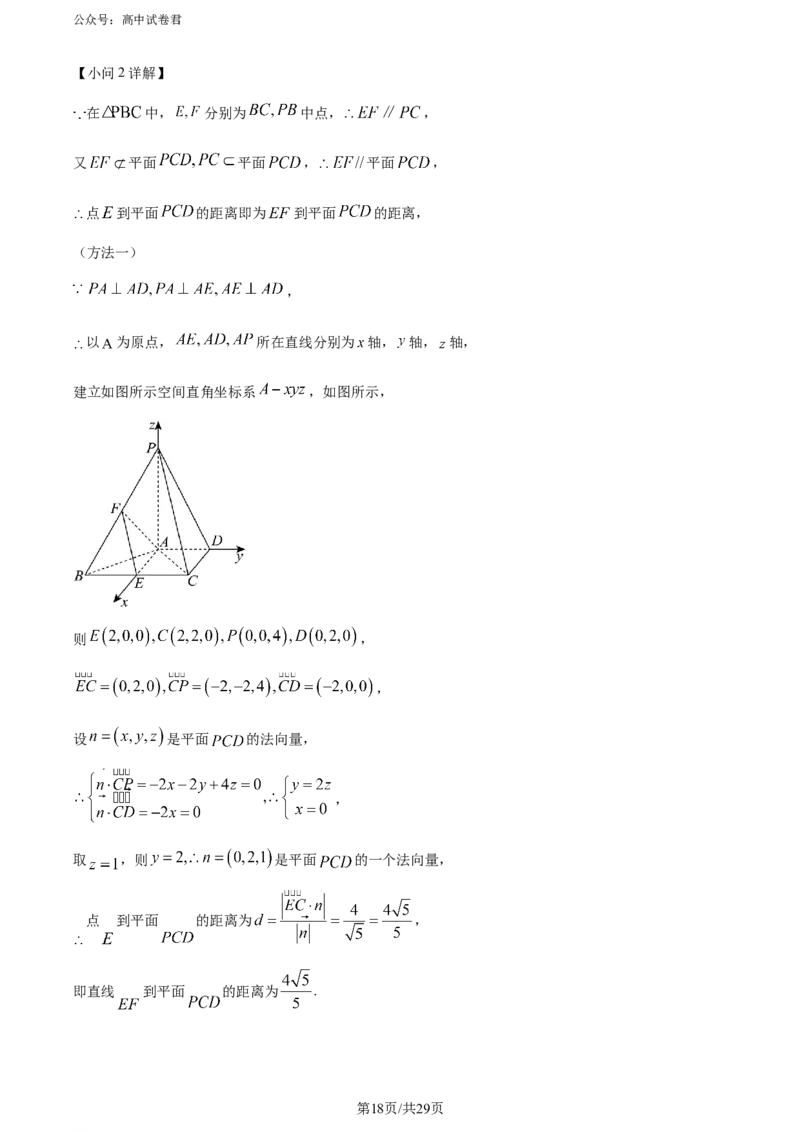
【小问2详解】
在 中, 分别为 中点, ,
又 平面 平面 , 平面 ,
点 到平面 的距离即为 到平面 的距离,
(方法一)
,
以 为原点, 所在直线分别为 轴, 轴, 轴,
建立如图所示空间直角坐标系 ,如图所示,
则 ,
,
设 是平面 的法向量,
,
取 ,则 是平面 的一个法向量,
点 到平面 的距离为 ,
即直线 到平面 的距离为 .
第18页/共29页
学科网(北京)股份有限公司公众号:高中试卷君
(方法二)
连接 、 ,如图所示,
为等腰直角三角形, ,
又 平面 是三棱锥 的高,
,
,
,
,
设 到平面 距离为 ,则 ,
,
即 到平面 的距离为 .
17. 已知点 ,直线 ,动圆 与直线 相切,交线段 于点 ,且 .
(1)求圆心 的轨迹方程,并说明是什么曲线;
(2)过点 且倾斜角大于 的直线 与 轴交于点 ,与 的轨迹相交于两点 ,且
第19页/共29页
学科网(北京)股份有限公司公众号:高中试卷君
,求 的值及 的取值范围.
【答案】(1) ,点 的轨迹是焦点在 轴上,实轴长、虚轴长均为 的等轴双曲线.
(2) ,
【解析】
【分析】(1)设点 ,根据 列出等量关系整理可得;
(2)设直线 ,联立双曲线方程,利用韦达定理结合 ,可得 的
值及 的取值范围.
【小问1详解】
设点 ,圆 的半径为 为 到直线 的距离,则 .
根据题意,动点 的轨迹就是点的集合
即 ,整理得 .
所以,点 的轨迹是焦点在 轴上,实轴长、虚轴长均为 的等轴双曲线.
【小问2详解】
设直线 ,
第20页/共29页
学科网(北京)股份有限公司公众号:高中试卷君
倾斜角大于
设
联立 得 ,
故 , , ,
由题知,双曲线的焦点 ,
由 得 的取值范围是
18. 短视频已成为当下宣传的重要手段,东北某著名景点利用短视频宣传增加旅游热度,为调查某天南北
方游客来此景点旅游是否与收看短视频有关,该景点对当天前来旅游的500名游客调查得知,南方游客有
300人,因收看短视频而来的280名游客中南方游客有200人.
(1)依据调查数据完成如下列联表,根据小概率值 的独立性检验,分析南北方游客来此景点旅
游是否与收看短视颍有关联:单位:人
短视频
游客 合计
收看 未看
南方游
客
第21页/共29页
学科网(北京)股份有限公司公众号:高中试卷君
北方游
客
合计
(2)为了增加游客的旅游乐趣,该景点设置一款5人传球游戏,每个人得到球后都等可能地传给其余4人
之一,现有甲、乙等5人参加此游戏,球首先由甲传出.
(i)求经过 次传递后球回到甲的概率;
(ii)记前 次传递中球传到乙的次数为 ,求 的数学期望.
参考公式: ,其中 ;
附表:
0.1 0.05 0.01 0.005 0.001
2.706 3.841 6.635 7.879 10.828
【答案】(1)列联表见解析,无关
(2)(i) ;(ii)
【解析】
【分析】(1)利用已知条件,完成列联表,利用独立性检验公式求解判断即可;
(2)(i)设经过 次传递后回到甲的概率为 ,求出关系式,得到通项公式;(ii)方法一:设第 次传
递时甲接到球的次数为 ,则 服从两点分布, ,设前 次传递中球传到甲的次数为 ,利用
公式求期望即可.方法二:设第 次传递时,乙接到球的概率和次数分别为 与 ,则 服从两点分布,
,利用公式求期望即可.
【小问1详解】
将所给数据进行整理,得到如下列联表:
游客 短视频 合计
第22页/共29页
学科网(北京)股份有限公司公众号:高中试卷君
收看 未看
南方游
200 100 300
客
北方游
80 120 200
客
合计 280 220 500
零假设 :南北方游客来此景点旅游与短视频无关联.
根据小概率值 的独立性检验,我们推断 不成立,
即认为南北方游客来此景点旅游与收看短视频有关联,此推断犯错误的概率不大于0.001
【小问2详解】
(i)设经过 次传递后回到甲的概率为 ,
, ,
又 ,
所以 是首项为 ,公比为 的等比数列,
所以 .
(ii)(方法一)
设第 次传递时甲接到球的次数为 ,则 服从两点分布, ,
设前 次传递中球传到甲的次数为 ,
第23页/共29页
学科网(北京)股份有限公司公众号:高中试卷君
,
因为 ,所以 .
(方法二)
设第 次传递时,乙接到球的概率和次数分别为 与 ,则 服从两点分布,
,由题可知 , ,
又 ,所以 ,所以 是首项为 ,公比为 的等比数列,
, ,
,
故 .
【点睛】关键点点睛:本题第2问(ii)的解决关键是,根据题意得到 的关系,利用构造法分析出
是首项为 ,公比为 的等比数列,由此得解.
19. 已知函数 .
(1)讨论 的单调性;
(2)设 分别是 的极小值点和极大值点,记 .
第24页/共29页
学科网(北京)股份有限公司公众号:高中试卷君
(i)证明:直线 与曲线 交于除 外另一点 ;
(ii)在(i)结论下,判断是否存在定值 且 ,使 ,若存在,请求出 的值;
若不存在,请说明理由.
【答案】(1) 在 上单调递增,在 上单调递减
(2)(i)证明见解析;(ii)存在定值 ,此时 .
【解析】
【分析】(1)求定义域,求导,对导函数因式分解,从而解不等式,求出函数单调性;
(2)(i)法一:在(1)基础上得到 ,求出 直线方程,联立得到
,变形得到 ,构造 ,
求导得到其单调性,结合零点存在性定理得到结论;
法二:在(1)基础上得到 ,求出 直线方程,联立得到 ,
变形得到 ,构造 ,求导得到其单调性,结合零点
存在性定理得到结论;
(ii)法一:在(i)基础上,得到 ,表达出 ,
故 , 结 合 ( i ) 中 的 得 到 , 换 元 得 到
,求导得到其单调性,结合特殊点的函数值,得到存在定值 ,且 ,使
,又 ,故 ;
第25页/共29页
学科网(北京)股份有限公司公众号:高中试卷君
法二:由(i)知, ,表达出 ,
故 ,根据 ,得到 ,又 ,故 ;
【小问1详解】
定义域为R,
,
令 ,则 ,令 , 或 ,
在 上单调递增,在 上单调递减.
【小问2详解】
(i)法一:由(1)知 且 ,
,
,
直线方程为 ,
令 ,即 ,
或 ,
设 ,则 ,
令 ,则 ,
,
第26页/共29页
学科网(北京)股份有限公司公众号:高中试卷君
令 ,则 ,令 ,则 ,
在 上单调递减,在 上单调递增,
, ,
(或者 )
存在唯一的 ,使 ,即 ,
故方程①的解有
综上,直线 与曲线 交于除 点外另一点 ;
法二:由(1)知 且 ,
,
,
直线方程为 ,
令 ,即 ,
或 ,
设 ,则 ,
令 ,则 ;令 ,则 ;令 ,则 ,
在 上单调递增,在 上单调递减,
,
第27页/共29页
学科网(北京)股份有限公司公众号:高中试卷君
,使得 ,
故方程①的解有 ,
综上,直线 与曲线 交于除 点外另一点 .
(ii)法一:由(i)知, ,
,
,
由(i)可知, ,
,
即 ,
,
设 ,设 ,
,
令 ,则 ,
令 ,则 ,令 ,则 ,
在 上单调递减,在 上单调递增.
第28页/共29页
学科网(北京)股份有限公司公众号:高中试卷君
,
,使 ,此时 ,
故存在定值 ,且 ,使 ,
又 ,故 ;
法二:(ii)由(i)知, ,
,
,
,
,
,
,
故存在定值 ,且 ,使 ,此时 .
【点睛】方法点睛:隐零点的处理思路:
第一步:用零点存在性定理判定导函数零点的存在性,其中难点是通过合理赋值,敏锐捕捉零点存在的区
间,有时还需结合函数单调性明确零点的个数;
第二步:虚设零点并确定取范围,抓住零点方程实施代换,如指数与对数互换,超越函数与简单函数的替
换,利用同构思想等解决,需要注意的是,代换可能不止一次.
第29页/共29页
学科网(北京)股份有限公司