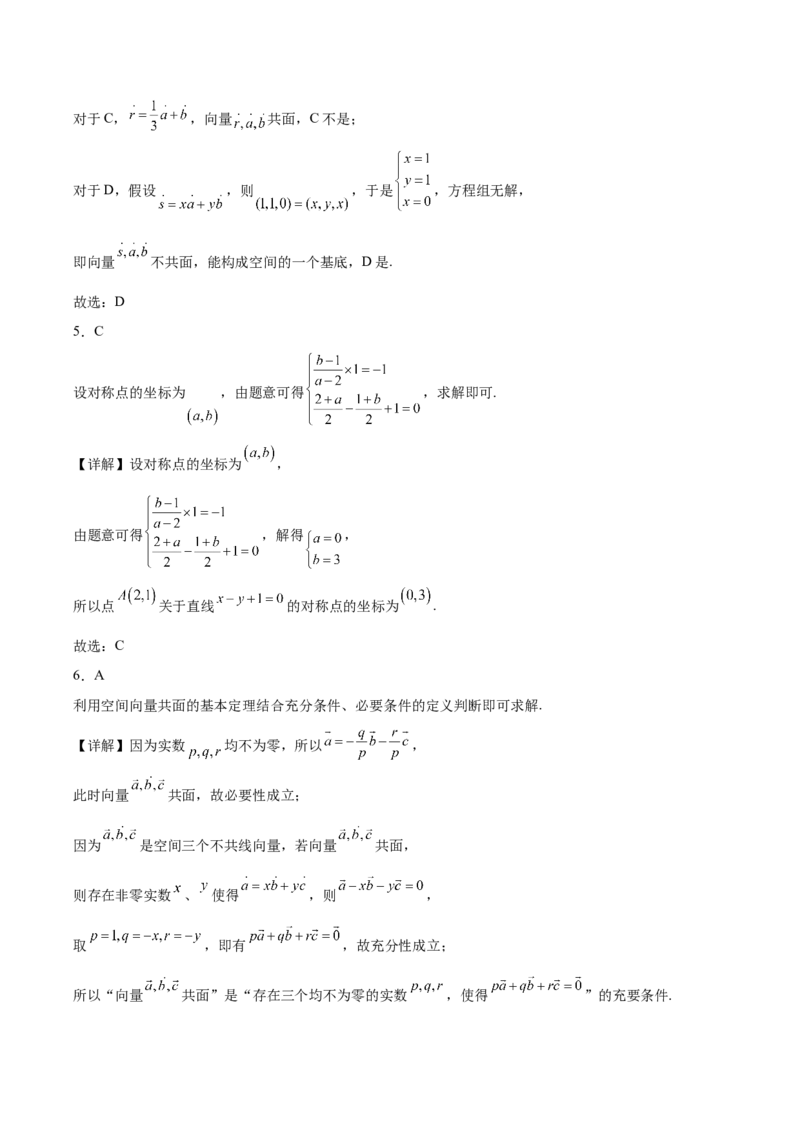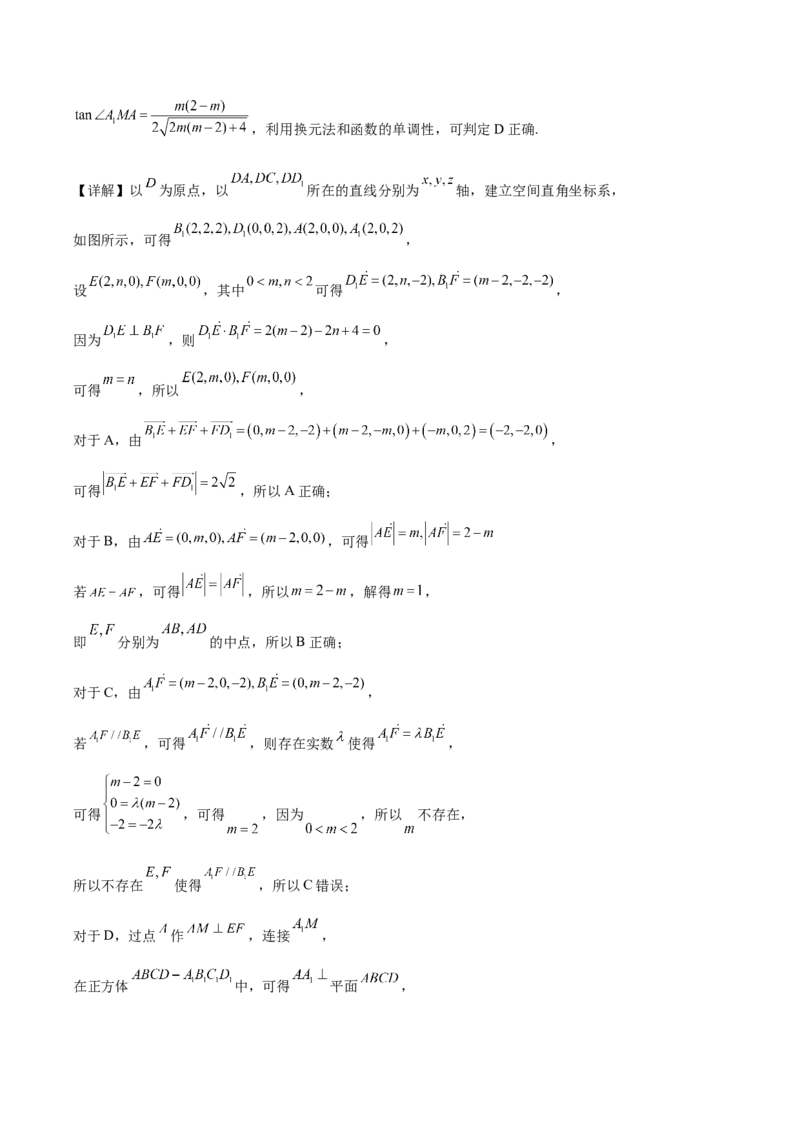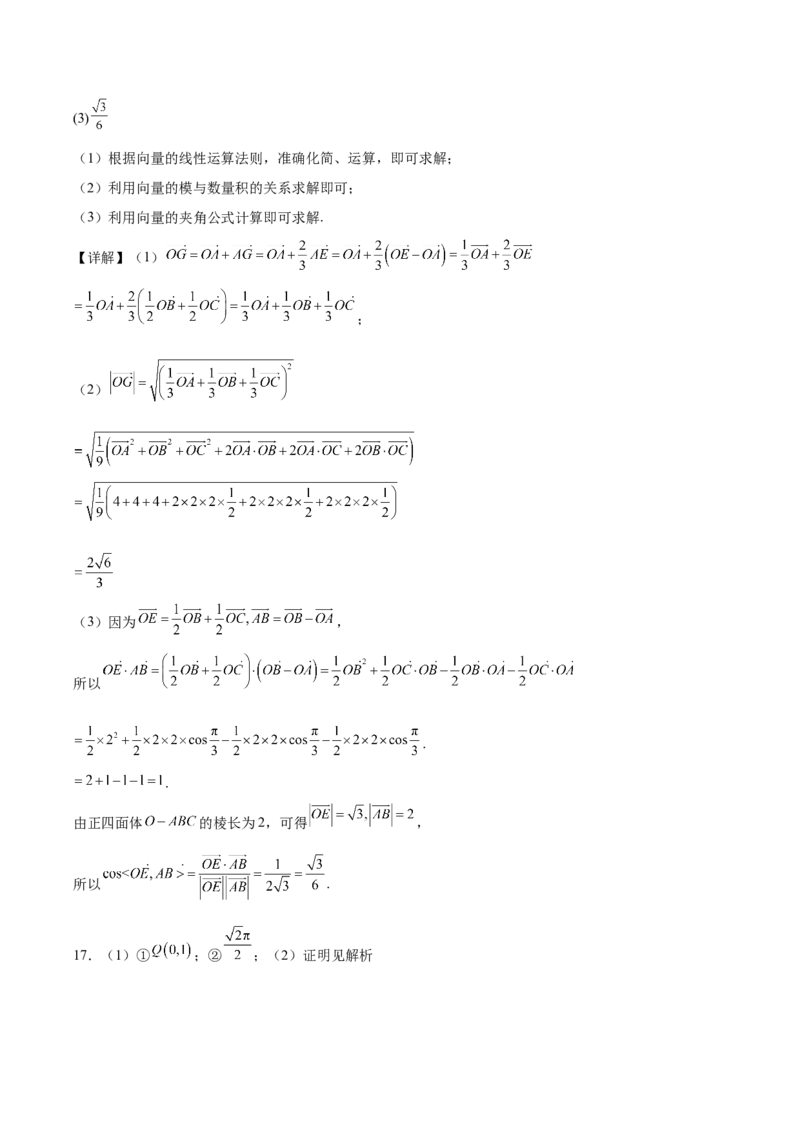文档内容
江苏省南通市2025-2026学年高二上学期期中调研测试
数学试题
一、单选题
1.直线 的倾斜角为( )
A. B. C. D.
2.已知直线 与 平行,则 ( )
A.4 B.5 C.6 D.7
3.若方程 : 表示圆,则实数 的取值范围是( )
A. B. C. D.
4.若空间向量 ,则下列向量能与 构成空间的一个基底的是( )
A. B.
C. D.
5.点 关于直线 的对称点的坐标为( )
A. B. C. D.
6.已知 是空间三个不共线向量,则“向量 共面”是“存在三个均不为零的实数 ,使得
”的( )
A.充要条件 B.充分不必要条件
C.必要不充分条件 D.既不充分也不必要条件
7.在正三棱柱 中, ,则直线 与 所成角的余弦值为( )A. B. C.0 D.
8.已知直线 和圆 交于 两点,设线段 的中点为 为坐标
原点,则 的最大值为( )
A. B. C. D.
二、多选题
9.已知三条直线 和 不能围成一个三角形,则实数 的可能取值为
( )
A. B.3 C. D.
10.已知圆 与圆 ,则( )
A.圆心距
B.两圆的公共弦所在直线的方程为
C.两圆的公共弦长为
D.直线 是两圆的一条公切线
11.在棱长为2的正方体 中, 分别是棱 上的动点(不含端点),且
,则( )
A.
B.当且仅当 为 中点时,C.存在 ,使得
D.直线 与平面 所成角的正弦值的最大值为
三、填空题
12.已知向量 , ,且 ,则 .
13.过点 作圆 的切线,则切线长为 .
14.已知两条直线 和 都经过点 ,则两点 , 间的最短
距离为 .
四、解答题
15.已知 的三个顶点为 .
(1)求 边上的中线 的长;
(2)求 的外接圆方程.
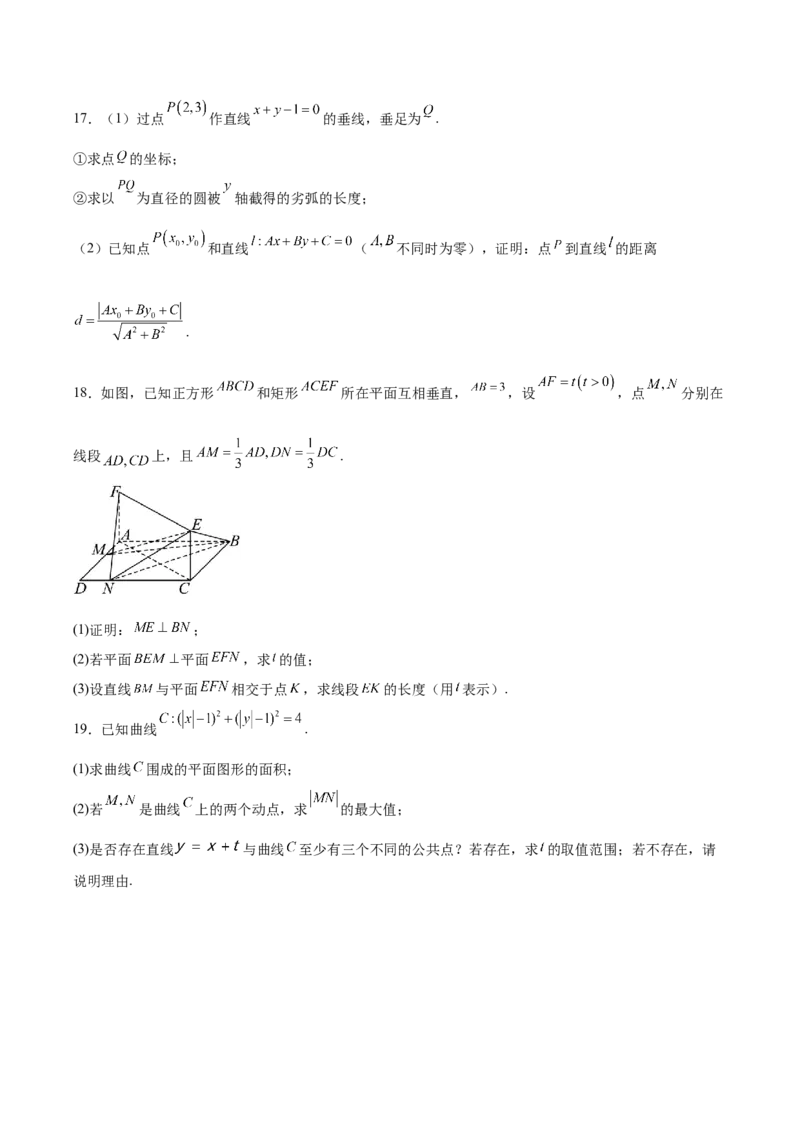
16.如图,在棱长为2的正四面体 中,已知 是线段 的中点,点 在线段 上,且
.
(1)用向量 表示 ;
(2)求 ;
(3)求向量 与 夹角的余弦值.17.(1)过点 作直线 的垂线,垂足为 .
①求点 的坐标;
②求以 为直径的圆被 轴截得的劣弧的长度;
(2)已知点 和直线 ( 不同时为零),证明:点 到直线 的距离
.
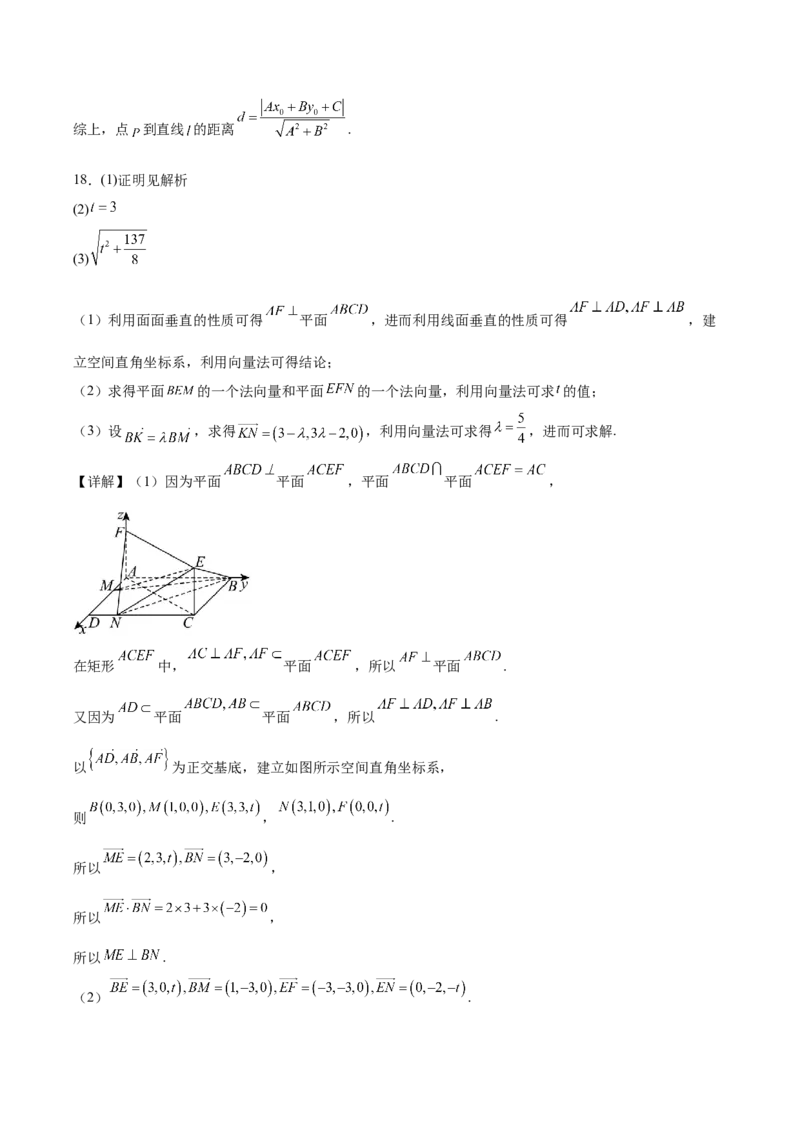
18.如图,已知正方形 和矩形 所在平面互相垂直, ,设 ,点 分别在
线段 上,且 .
(1)证明: ;
(2)若平面 平面 ,求 的值;
(3)设直线 与平面 相交于点 ,求线段 的长度(用 表示).
19.已知曲线 .
(1)求曲线 围成的平面图形的面积;
(2)若 是曲线 上的两个动点,求 的最大值;
(3)是否存在直线 与曲线 至少有三个不同的公共点?若存在,求 的取值范围;若不存在,请
说明理由.题号 1 2 3 4 5 6 7 8 9 10
答案 A D B D C A B D BCD ABD
题号 11
答案 ABD
1.A
根据直线方程求出直线斜率,再根据斜率和倾斜角间的关系即可求出倾斜角.
【详解】 可化为: ,
∴直线的斜率为 ,设直线的倾斜角 ,则 ,
∵ ,∴ .
故选:A.
2.D
利用两直线平行的充要条件列式求解即可.
【详解】由直线 与 平行,
得 ,所以 .
故选:D.
3.B
根据二元二次方程表示圆的条件,列出不等式,解之即可.
【详解】因为方程 : 表示圆,
则有 ,解得: ,
故选:B.
4.D
根据给定条件,利用空间向量的坐标运算及空间基底的意义判断即得.
【详解】对于A, ,向量 共面,A不是;
对于B, ,向量 共面,B不是;对于C, ,向量 共面,C不是;
对于D,假设 ,则 ,于是 ,方程组无解,
即向量 不共面,能构成空间的一个基底,D是.
故选:D
5.C
设对称点的坐标为 ,由题意可得 ,求解即可.
【详解】设对称点的坐标为 ,
由题意可得 ,解得 ,
所以点 关于直线 的对称点的坐标为 .
故选:C
6.A
利用空间向量共面的基本定理结合充分条件、必要条件的定义判断即可求解.
【详解】因为实数 均不为零,所以 ,
此时向量 共面,故必要性成立;
因为 是空间三个不共线向量,若向量 共面,
则存在非零实数 、 使得 ,则 ,
取 ,即有 ,故充分性成立;
所以“向量 共面”是“存在三个均不为零的实数 ,使得 ”的充要条件.故选:A
7.B
利用正三棱柱的性质计算出 , , ,再根据夹角公式即可求解.
【详解】由题意 ,同理可得 ,
因为 平面 , 平面 ,所以 , 即 ,
所以
,
所以 ,
故直线 与 所成角的余弦值为 .
故选:B
8.D
易知直线l过定点 ,且点 在圆 内,结合 垂直于 ,可得动点 的轨迹方程为
,由此容易得出 的最大值.
【详解】将圆 的方程化为标准方程为 ,则圆心为 ,
直线 ,易知直线恒过定点又 ,所以点 在圆内,如图所示:
由于 垂直于 ,则点 的轨迹为以 为直径的圆,
线段 的中点坐标为 , ,
所以动点 的轨迹方程为 ,
又 , ,
可得 ,
即 的取值范围为 ,
所以 的最大值为 .
故选:D
9.BCD
利用直线平行以及三条直线交于一点,即可求解.
【详解】联立 ,可得 ,即两直线交点为 .
当 时,直线 和直线 平行,不能围成三角形;
当 时,直线 和直线 平行,不能围成三角形;
当 时,直线 经过点 ,三线共点,不能围成三角形;
当 时,三条直线两两相交且不共点,可以围成三角形,不符合题意.故选:BCD
10.ABD
根据圆的方程确定圆心坐标后计算圆心距,可得A;两圆方程相减得出公共弦所在直线方程,再在其中一个
圆中计算公共弦弦长可判断B,C;计算两个圆到给定直线的距离是否分别等于各自半径,可判断D.
【详解】根据两圆方程,可知圆 的圆心坐标 ,半径 ,圆 的圆心坐标 ,半径 .
对于A: ,故A正确;
对于B:由A可知, ,因此两圆相交.两圆的公共弦所在直线方程可由两圆方程相
减得到,即将 减去 ,
得到 ,整理化简得 ,故B正确;
对于C:两圆相交,存在公共弦,在其中一个圆中计算该弦长即可.圆心 到公共弦 的距
离 ,故弦长 ,故C错误;
对于D:圆心 到直线 的距离 ,圆心 到直线 的
距离 ,故直线 是两圆的一条公切线,故D正确.
故选:ABD.
11.ABD
以 为原点,建立坐标系,设 ,根据 ,求得 ,由
,可判定A正确;由 ,求得 ,可判定B正确;由 ,
列方程方程组,可判定C错误;过 作 ,证得 即为直线 与平面 所成角,求得,利用换元法和函数的单调性,可判定D正确.
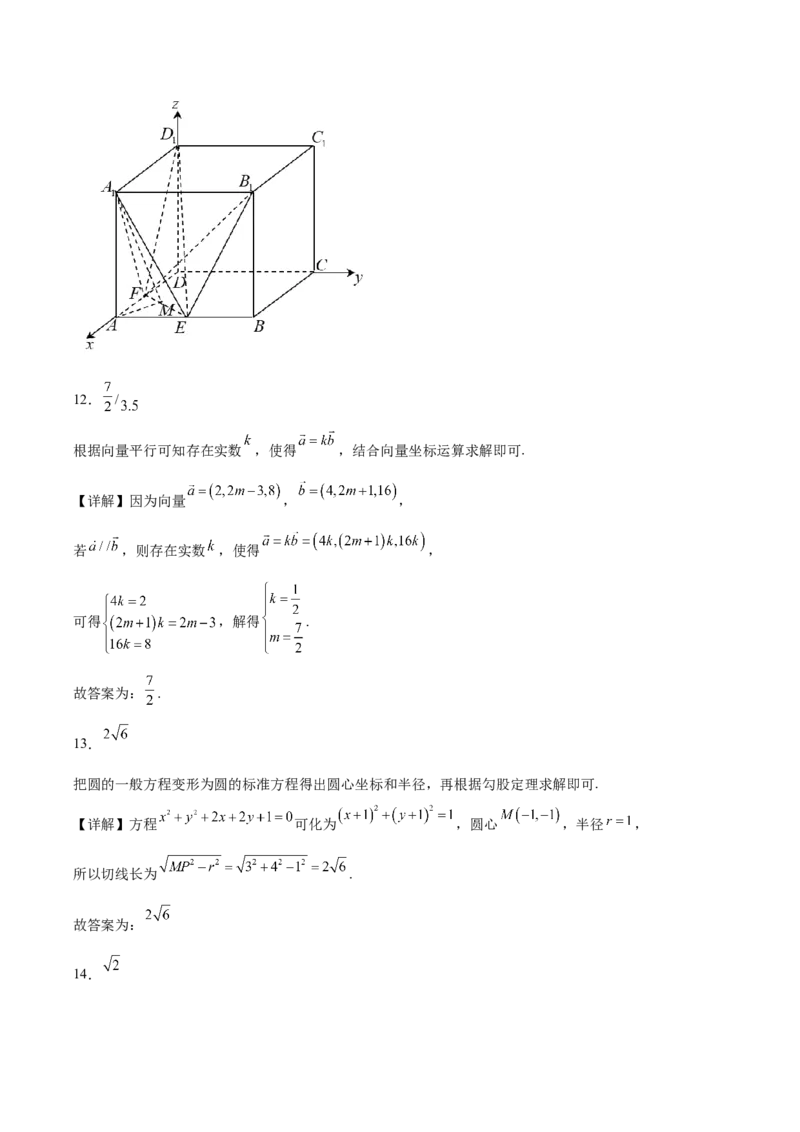
【详解】以 为原点,以 所在的直线分别为 轴,建立空间直角坐标系,
如图所示,可得 ,
设 ,其中 可得 ,
因为 ,则 ,
可得 ,所以 ,
对于A,由 ,
可得 ,所以A正确;
对于B,由 ,可得
若 ,可得 ,所以 ,解得 ,
即 分别为 的中点,所以B正确;
对于C,由 ,
若 ,可得 ,则存在实数 使得 ,
可得 ,可得 ,因为 ,所以 不存在,
所以不存在 使得 ,所以C错误;
对于D,过点 作 ,连接 ,
在正方体 中,可得 平面 ,因为 平面 ,所以 ,
又因为 ,且 平面 ,所以 平面 ,
因为 平面 ,所以平面 平面 ,
所以 即为直线 与平面 所成角,
在直角 中,由 ,可得 ,
所以
在直角 中,可得 ,
令 ,其中 ,
可得 ,且 ,所以 ,
由函数 在 上单调递减,
所以当 时, ,所以 的最大值为 ,
所以 的最大值为 ,所以D正确.
故选:ABD.12. /
根据向量平行可知存在实数 ,使得 ,结合向量坐标运算求解即可.
【详解】因为向量 , ,
若 ,则存在实数 ,使得 ,
可得 ,解得 .
故答案为: .
13.
把圆的一般方程变形为圆的标准方程得出圆心坐标和半径,再根据勾股定理求解即可.
【详解】方程 可化为 ,圆心 ,半径 ,
所以切线长为 .
故答案为:
14.确定 , 分别在直线 上,由平行线间距离即可求解.
【详解】因为两条直线 和 都经过点 ,
所以 , ,
所以 , 分别在直线 上,
所以两点 , 间的最短距离为两平行线间距离,即 ,
故答案为:
15.(1)
(2)
(1)利用中点坐标公式得到中点坐标,再利用两点间距离公式求解长度即可.
(2)设出外接圆的方程,代入点的坐标,进而求解参数得到方程即可.
【详解】(1)由中点坐标公式得 的中点 ,
由两点间距离公式得 .
(2)设三角形外接圆方程为 ,
因为点 在所求的圆上,可得 ,解得 ,
则 外接圆的方程为 .
16.(1)
(2)(3)
(1)根据向量的线性运算法则,准确化简、运算,即可求解;
(2)利用向量的模与数量积的关系求解即可;
(3)利用向量的夹角公式计算即可求解.
【详解】(1)
;
(2)
(3)因为 ,
所以
.
.
由正四面体 的棱长为2,可得 ,
所以 .
17.(1)① ;② ;(2)证明见解析(1)①求得直线 的方程,联立方程求解即可;②求得圆的方程,由勾股定理可得 ,计算即
可求解;
(2)方法一:求得过点 和直线 垂直的直线方程,联立方程组求得交点坐标,由
平面中两点间的距离公式即可得证;方法二:过点 分别作 轴、 轴的垂线,分别与 相交于
,由等面积法计算即可得证.
【详解】(1)①因为直线 的斜率 ,
所以其垂线的斜率 ,
所以直线 的方程为 .
联立 ,解得 .
②因为 ,
所以以 为直径的圆的圆心 ,半径 ,
所以圆 的方程为 .
设圆 与 轴交于 两点,则 ,
所以 ,
所以 ,所以所求弧长为 .
(2)法一:设 ,过点 作直线 的垂线,垂足为 ,
则过点 和直线 垂直的直线方程为 .
联立 ,解得 ,所以点 的坐标为 .
所以
当 时,
.
当 时,
.
所以点 到直线 的距离 .
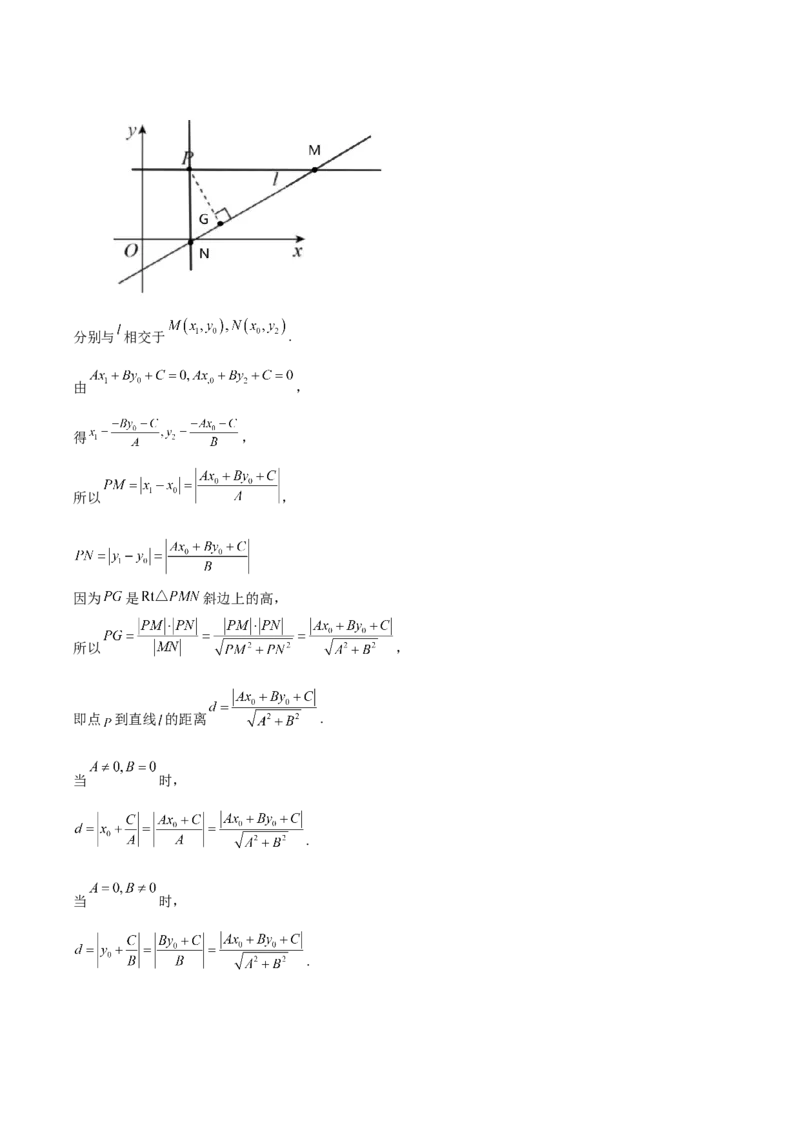
法二:过点 作 ,垂足为 .
当 时,
过点 分别作 轴、 轴的垂线,分别与 相交于 .
由 ,
得 ,
所以 ,
因为 是 斜边上的高,
所以 ,
即点 到直线 的距离 .
当 时,
.
当 时,
.综上,点 到直线 的距离 .
18.(1)证明见解析
(2)
(3)
(1)利用面面垂直的性质可得 平面 ,进而利用线面垂直的性质可得 ,建
立空间直角坐标系,利用向量法可得结论;
(2)求得平面 的一个法向量和平面 的一个法向量,利用向量法可求 的值;
(3)设 ,求得 ,利用向量法可求得 ,进而可求解.
【详解】(1)因为平面 平面 ,平面 平面 ,
在矩形 中, 平面 ,所以 平面 .
又因为 平面 平面 ,所以 .
以 为正交基底,建立如图所示空间直角坐标系,
则 , .
所以 ,
所以 ,
所以 .
(2) .设平面 的一个法向量为 ,
则 ,即 ,令 ,得 ,
所以平面 的一个法向量为 .
设平面 的一个法向量为 ,则
,即 ,令 ,得 ,
所以平面 的一个法向量为 .
若平面 平面 ,则 ,
得 ,解得 ,
因为 ,所以 .
(3)设 ,则 ,所以 .
由(2)可知,平面 的一个法向量 ,所以 ,
得 ,解得 .
所以 ,所以 ,
所以 .
19.(1)(2)
(3)不存在,理由见解析
【详解】(1)曲线 既关于两坐标轴成轴对称,又关于原点成中心对称.
当 时,曲线方程为 .
记圆心为 ,与 轴分别交于 两点,
则 ,过点 作 ,
则 ,
所以 ,
所以 .
所以 ,
所以 ,同理 .
由对称性可知,曲线 围成的平面图形的面积
.
(2)记曲线 在第一象限的圆心为 ,第二象限的圆心为 ,
第三象限的圆心为 、第四象限的圆心为 .情况1:不妨 都在第一象限(或坐标轴正半轴), .
情况2:不妨 在第一象限(或坐标轴正半轴), 在第二象限(或 轴负半轴)时,
(当且仅当 四点共线时等号成立),此时 最大值为6.
情况 不妨 在第一象限(或坐标轴正半轴), 在第三象限(或坐标轴负半轴)时,
(当且仅当 四点共线时
等号成立),此时 最大值为 .
综上,根据对称性可知 最大值为 .
(3)当 时,研究直线与曲线 在第一象限的公共点.
联立 ,得 (*).
因为 ,
所以方程(*)只有一个正根,则直线 与曲线 在第一象限只有一个公共点.
同理,直线 与曲线在第三象限也只有一个公共点.
因此,当 时,直线 与曲线 只有两个公共点.
当 时,
一方面,直线 与曲线 在第二象限的部分至多两个公共点.
另一方面,由 ,得 (*).因为 ,
所以方程(*)无正根,即直线 与曲线 在第一象限无公共点.
同理,直线 与曲线 在第三象限无公共点.
所以当 时,直线 与曲线 至多两个公共点.
所以 时,直线 与曲线 至多两个公共点.
由对称性可知, 时,直线 与曲线 也至多两个公共点.