数学答案_2024-2025高三（6-6月题库）_2024年10月试卷_1026广东省惠州市2025届高三第二次调研考试_广东省惠州市2025届高三第二次调研考试数学

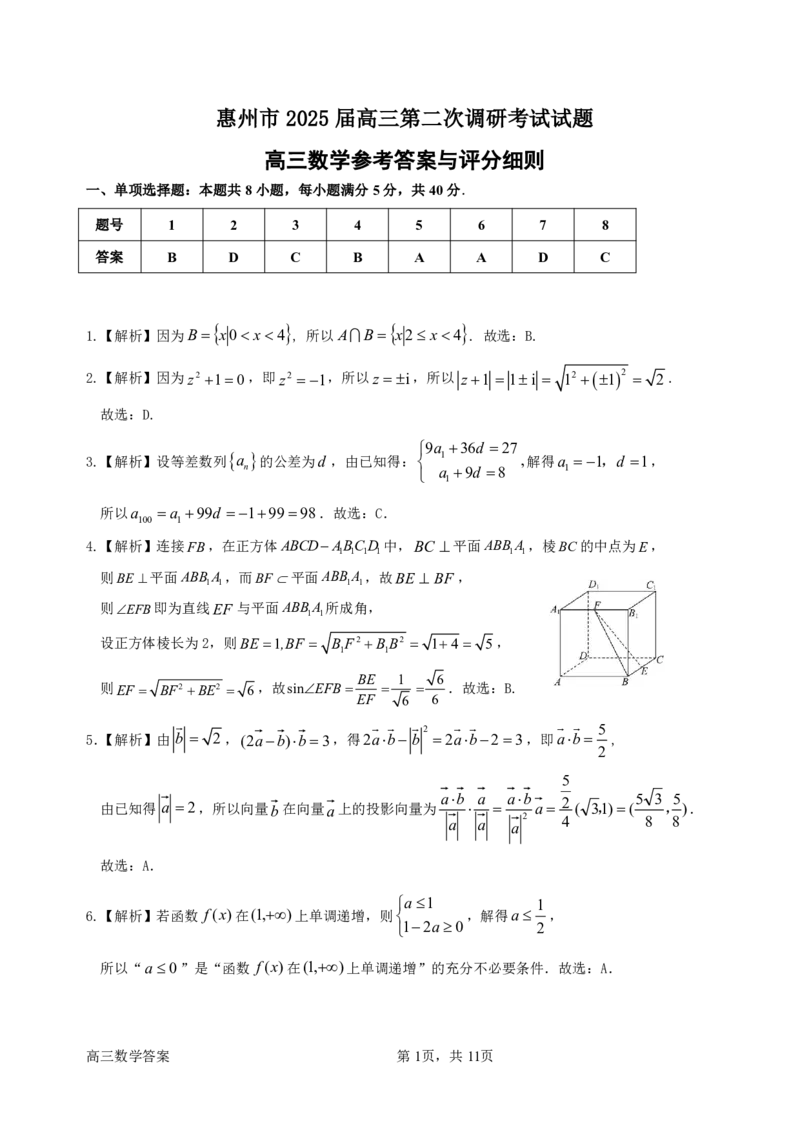
惠州市 2025 届高三第二次调研考试试题 高三数学参考答案与评分细则 一、单项选择题：本题共8小题，每小题满分5分，共40分． 题号 1 2 3 4 5 6 7 8 答案 B D C B A A D C     1.【解析】因为B  x0 x4 , 所以AB  x2 x4 . 故选：B. 2.【解析】因为z2 10，即z2 1，所以z i，所以 z1  1i  12 1 2  2 . 故选：D. 9a 36d 27 3.【解析】设等差数列  a  的公差为d ，由已知得： 1 ,解得a 1，d 1， n  a 9d 8 1 1 所以a a 99d 19998．故选：C． 100 1 4.【解析】连接FB，在正方体ABCDABCD 中，BC 平面ABBA ，棱BC的中点为E， 1 1 1 1 1 1 则BE 平面ABBA ，而BF平面ABBA ，故BE  BF ， 1 1 1 1 则EFB即为直线EF 与平面ABBA 所成角， 1 1 设正方体棱长为2，则BE 1,BF  BF2 BB2  14  5， 1 1 BE 1 6 则 EF  BF2BE2  6 ，故sinEFB   ．故选：B. EF 6 6     2     5 5．【解析】由 b  2，(2ab)b3，得2ab b 2ab23，即ab , 2 5 ab a ab 5 3 5 由已知得 a 2，所以向量b在向量a上的投影向量为   a  2 ( 3，1)( ，)． a a a 2 4 8 8 故选：A． a1 1 6.【解析】若函数 f(x)在(1,)上单调递增，则 ，解得a ， 12a0 2 所以“a0”是“函数 f(x)在(1,)上单调递增”的充分不必要条件．故选：A． 高三数学答案 第1页，共11页 {#{QQABLQAAogAgAgAAAQgCQQkwCgCQkhCCAQgOwFAIIAIAyBFABAA=}#}7.【解析】设优弧BC所在圆的圆心为O,半径为 ,连接OA,OB,OC .易知“水滴”的“竖直高度” OAR 4 5 为OAR,“水平宽度”为2R, 由题意知  ,解得OA R. 因为AB与圆弧相切于点B, 2R 3 3 OB R 3  所以OB  AB.在RtABO中, sinBAO    ，又BAO(0, ), OA 5 5 2 R 3 4 所以cosBAO  1sin2BAO  ，由对称性知,BAO CAO,则 BAC 2BAO, 5 3 4 24 所以sinBAC 2sinBAOcosBAO 2   .故选：D. 5 5 25 8.【解析】根据已知条件设理科女生有x 人，理科男生有x 人；文科女生有 y 人，文科男生有y 人； 1 2 1 2 根据题意可知：x x  y  y ，x y  x  y ， 1 2 1 2 1 1 2 2 根据同向不等式可加的性质有：x x x y  y  y x  y ，即x  y ，所以理科女生多于文 1 2 1 1 1 2 2 2 1 2 科男生，C正确. 其他选项没有足够证据论证. 故选：C. 二、多项选择题：本题共3小题，每小题满分6分，共18分。在每小题给出的四个选项中，有多项符合 题目要求。全部选对得6分，部分选对得部分分，有选错的得0分。 题号 9 10 11 全部正确选项 AD ABD ACD 9.【解析】数据从小到大排列为:1，1，2，3，3，3，3，4，5，5． 对于A，该组数据的极差为514，故A正确； 12234452 对于B，众数为3，平均数为 3，两者相等，故B错误； 10 1 对于C，方差为 (13)22(23)21(33)24(43)21(53)221.8，故C错误；   10 对于D，1080% 8，这组数据的第80百分位数为第8个数和第9个数的平均数4.5，故D正确． 故选：AD． 10.【解析】由图像可知： f x 2， A  2 ； max 高三数学答案 第2页，共11页 {#{QQABLQAAogAgAgAAAQgCQQkwCgCQkhCCAQgOwFAIIAIAyBFABAA=}#}又 f 02sin1，故sin 1 ，又  ，所以  ，所以A项正确； 2 2 6 7 7  7  已知 f  2sin  0，由五点作图法可知：  ，解得：2，所以B项正确； 12  12 6 12 6     故 f x2sin2x ；则xf(x )2xsin2x ，设h(x) xf(x )2xsin2x，  6  12 12  则h(x)2(x)sin(2x)2xsin2xh(x)，所以函数y xf(x )是偶函数，故C项错误； 12         g(x) f(x )2sin 2(x ) 2sin(2x )2cos (2x )     6  6 6 6 2 6    2cos( 2x)2cos(2x )，所以D项正确； 3 3 故选：ABD. 2 11.【解析】A选项，经验算，点( ,0)和(1,1)的坐标满足曲线L的方程：x2 (y x)2 1，所以点 2 2 ( ,0)和(1,1)均在L上，故A项正确； 2 B选项，OP  x2  y2 ，因为曲线L：x2 (y x)2 1关于 y轴对称，当x0时，x2 (yx)2 1，    设xcos,yxsin，  , ，    2 2 1cos2 所以 OP 2  x2  y2 cos2(cossin)2 1 sin2 2 3 1 3 5 1  sin2 cos2  sin(2)，其中tan ， 2 2 2 2 2 3 5 51 3 5 51 所以 OP    ， OP    ，所以 OP 的最大值和最小值之和 min 2 2 2 max 2 2 2 为 5，故B项错误； C选项，因为曲线L：x2 (y x)2 1关于 y轴对称，当x0时，x2 (yx)2 1， 则(yx)2 1x2，所以y  x 1x2 ，因求点P的纵坐标的最大值，故取y  x 1x2 ， 1 又 y2 （x 1x2）2 12x 1x2 12 x2(1x2) 1x2 (1x2)2(当且仅当 x2  时 2 等号成立)，所以y 2 ，故C项正确； 高三数学答案 第3页，共11页 {#{QQABLQAAogAgAgAAAQgCQQkwCgCQkhCCAQgOwFAIIAIAyBFABAA=}#}y2 x2 D选项， PA  PB 2 3等价于点P在椭圆  1内（包含椭圆），由B项可知，即满足： 3 2 3(1cos2) 2(cossin)2 3cos26，即2(1sin2) 6，整理得： 2 3 4sin23cos25，即5sin(2)5，其中其中tan ，即sin(2)1恒成立，则故 4 D项正确. 故选：ABD. 三、填空题：本题共3小题，每小题5分，共15分． 5 12. 32 13. 14. e2 5 12.【解析】当x1时，二项式展开式各项的系数和为25 32.故答案为：32. 13.【解析】由题意知 AF ac, FF 2c, FB ca，且三者成等比数列，则 FF 2  AF  FB 1 1 2 1 1 2 1 1 1 5 5 即4c2 (ca)(ca)c2 a2，所以e2  ，所以e . 故答案为： . 5 5 5 b 1 b 1 14.【解析】设方程ln(ax ) x2  的实根为x ，则ln(ax  ) x2  ， 2 4 0 0 2 0 4 b x2 1 b x2 1 所以ax  e 0 4 ，即ax  e 0 4 0. 0 2 0 2 y x2 1 设点P(a,b),则点P在直线x x e 0 4 0上. 0 2 x2 1 设点O(0,0)到直线x x y e x 0 2 1 4 0的距离为d ，则d  e 0 4 ， 0 2 x2  1 0 4 1 et 1 et(t1) 设t  x2  ， f(t) (t  )，则 f'(t) ， 0 4 t 2 t2 1  求得 f(t)在 ，1 上单调递减，在  1，  上单调递增，所以 f(t)  f(1)e，   2  min 则d  f(t)e，又a2 b2  OP 2,由几何意义可知 OP d ，所以a2 b2  OP 2 e2. 高三数学答案 第4页，共11页 {#{QQABLQAAogAgAgAAAQgCQQkwCgCQkhCCAQgOwFAIIAIAyBFABAA=}#} 3  3 b a  e 3  a e0  2 检验：当t 1时，x  ，由 2 2 ，解得 ； 0 2   e a2 b2 e2  b  2  3  3 b a  e  a e0  2 由 2 2 ，解得 ，所以则a2 b2可以取到最小值e2.   e a2 b2 e2  b  2 故答案为：e2. 四、解答题：本题共5小题，共77分．解答应写出文字说明、证明过程或演算步骤． 15．（本小题满分13分，其中第一小问6分，第二小问7分。） 1 1  1 【解析】（1）因为： f 1 10 ，所以切点坐标为：1, ，···························1分 2 2  2 2 又 fx x1 ， ·····························································································2分 x 所以 f12， ································································································3分 即所求切线的斜率为2. 1 所以切线方程为：y 2x1， ······································································· 5分 2 化简得：4x2y30， 所以曲线y f x在点(1，f 1)处的切线方程为4x2y30． ··························································································································6分 3 【注】切线方程写成 y 2x 不扣分 2 2 x2x2 x2x1 （2） fxx1   ，（x0） ········································8分 x x x 由 f'(x)0得x2；由 f'(x)0得0 x2. ············································10分 所以 f x在  1，2  上单调递减，在  2,e  上单调递增. ·················································11分 所以函数 f x在区间  1,e  上的极小值为 f 22ln2，也是最小值. 所以函数 f x在区间  1,e  上的最小值为2ln2. ························································································································ 13分 高三数学答案 第5页，共11页 {#{QQABLQAAogAgAgAAAQgCQQkwCgCQkhCCAQgOwFAIIAIAyBFABAA=}#}16．（本小题满分15分，其中第一小问5分，第二小问10分。） 【解析】（1）证明：已知PA底面ABCD，且BC底面ABCD， 所以PABC. ···································································································2分 由ACB90,可得BC  AC .············································································3分 又PAAC  A,PA,AC 平面PAC , ·································································4分 所以BC 平面PAC ． ······················································································ 5分 （2）取CD的中点E．由AB∥CD,BAD 120，可得ADC 60， 又因为AD CD 1，所以三角形ADC是正三角形，·················································6分 故 AE CD, AE  AB. ··················································································7分 在RtACB中，BAC 60,AC 1，所以AB 2. 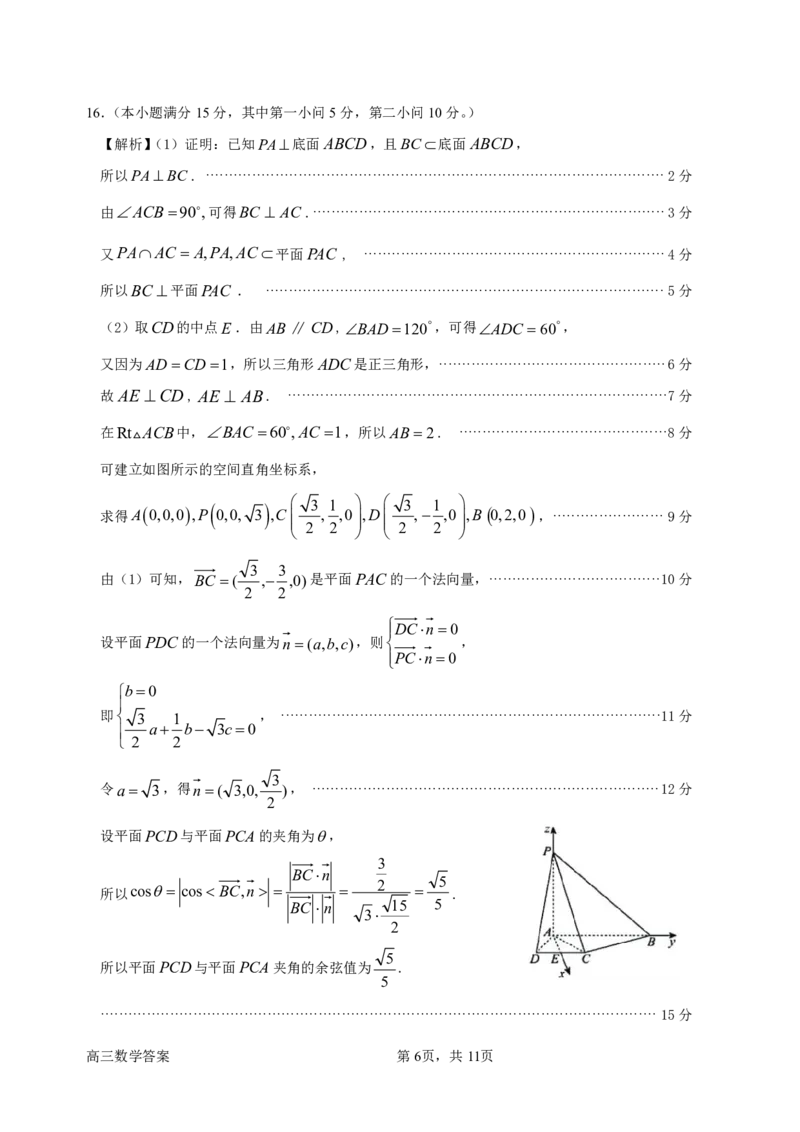·············································8分 可建立如图所示的空间直角坐标系，    3 1   3 1  求得A  0,0,0  ,P 0,0, 3 ,C , ,0,D ,  ,0,B  0,2,0  ，························ 9分     2 2 2 2     3 3 由（1）可知，BC ( , ,0)是平面PAC的一个法向量，·····································10分 2 2   DCn0 设平面PDC的一个法向量为n(a,b,c)，则 ，  PCn0 b0  即 3 1 ， ··················································································11分  a b 3c0  2 2 3 令a 3，得n( 3,0, )， ···········································································12分 2 设平面PCD与平面PCA的夹角为， 3 BCn 5 2 所以cos cos BC,n    . BC  n 15 5 3 2 5 所以平面PCD与平面PCA夹角的余弦值为 . 5 ························································································································ 15分 高三数学答案 第6页，共11页 {#{QQABLQAAogAgAgAAAQgCQQkwCgCQkhCCAQgOwFAIIAIAyBFABAA=}#}BCn 【注】写出公式cos cos BC,n  给一分，代入数据给一分，结果计算正确给一分 BC  n 17．（本小题满分15分，其中第一小问7分，第二小问8分。） x2  y2 1 【解析】(1)直线l与双曲线C有两个不同的交点，则方程组 有两组不同的实数根， y kx1 整理得(1k2)x2kx20. ···············································································2分 1k2 0  ，··············································································4分 4k24(1k2)(2)0 解得 2 k  2 且k  1， ··········································································6分 双曲线C与直线l有两个不同的交点时，k的取值范围是( 2,1)(1,1)(1, 2)． ··························································································································7分 （2）解法一：设交点A(x ,y ),B(x ,y )， 1 1 2 2 由(1)知双曲线C与直线l联立的方程为(1k2)x2kx20. 2k 2 由韦达定理得：x x  ,x x  ，···················································· 8分 1 2 1k2 1 2 1k2 则 AB  1k2 x x  1k2  (x x )2 4x x ··············································9分 2 1 2 1 1 2 2k 2 84k2  1k2  ( )2 4( )  1k2  ········································10分 1k2 1k2 1k2 1 又O到直线l的距离d  ， ········································································11分 1k2 1 2k2 所以OAB的面积S  AB d   2，·············································12分 OAB 2 1k2 6 解得k 0或k  ， ··················································································14分 2 6 又因为 2 k  2 且k  1，所以k 0或k  . 2 6 所以当k 0或k  时，OAB的面积为 2 . ··················································15分 2 高三数学答案 第7页，共11页 {#{QQABLQAAogAgAgAAAQgCQQkwCgCQkhCCAQgOwFAIIAIAyBFABAA=}#}【注】漏掉k 0扣一分 解法二：设交点A(x ,y ),B(x ,y )，直线l与y轴交于点D(0,1)， 1 1 2 2 由(1)知双曲线C与直线l联立的方程为(1k2)x2kx20. 2k 2 由韦达定理得：x x  ,x x  ，···················································· 8分 1 2 1k2 1 2 1k2 1 1 当A,B在双曲线的一支上且 x  x 时，S  S S  (x  x ) x x ； 1 2 OAB OAD OBD 2 1 2 2 1 2 1 1 当A,B在双曲线的两支上且x  x 时，S  S S  (x  x ) x x 1 2 OAB OAD OBD 2 1 2 2 1 2 1 综上，S  x x . ················································································10分 OAB 2 1 2 【注】未讨论两种情况、直接写对面积公式的扣一分 1 由已知得S  x x  2 ，故(x x )2 8，即(x x )2 4x x 8 OAB 2 1 2 1 2 1 2 1 2 2k 2 所以( )24( )8，········································································· 12分 1k2 1k2 6 解得k 0或k  ，·······················································································14分 2 6 又因为 2 k  2 且k  1，所以k 0或k  . 2 6 所以当k 0或k  时，OAB的面积为 2 .···················································15分 2 18．（本小题满分17分，其中第一小问10分，第二小问7分。） 【解析】（1）由abc，则A BC. ······························································· 1分  由ABC ，则ABC 3A，故0 A , ··············································2分 3 所以0 tan A 3， ·························································································· 3分 因为tan A为整数，所以tan A1， ········································································4分  3 解法一：由tan A1，可得A ，BC  . 因为A BC，所以B为锐角， 4 4     则  B ,所以 C  ，············································································ 6分 4 2 4 2 所以角A，B，C均为锐角，所以tan A，tanB，tanC 均为正整数， 又tan A1，所以tanC  tanB2, 高三数学答案 第8页，共11页 {#{QQABLQAAogAgAgAAAQgCQQkwCgCQkhCCAQgOwFAIIAIAyBFABAA=}#}3 1tanC 由tanB  tan( C) 2，································································8分 4 1tanC 解得tanC 3，所以tanB 2,tanC 3. 综上，tan A1，tanB 2，tanC 3. tan AtanB 12 经检验，当tan A1，tanB 2时，因为tan(AB)  3tanC 1tan AtanB 112 所以ABC ,符合题意. ··············································································10分 【注】未检验扣一分  3 解法二：由tan A1，可得A ，BC  . 4 4 3  3 因为 A BC ，所以  BC  2B,则  B ， 4 4 8 3 所以1 tanB tan . ···················································································6分 8 3 2tan 3 8 3 3 由tan  1，则tan2 2tan 10 ， 4 3 8 8 1tan2 8 3 3 解得tan 1 2或tan 1 2（舍去）， 8 8 故1tanB1 2 ， ························································································8分 又21 2 3，tanB为正整数，所以tanB 2，··················································9分 tan AtanB 12 所以tanC tan(AB)  3, 1tan AtanB 112 综上，tan A1，tanB 2，tanC 3. ····································································10分 2 5 10 3 10 （2）由（1）可知，tanB 2,tanC 3，则sinB  ,cosC  ,sinC  ， 5 10 10 ························································································································ 12分 a b c   在ABC中，由正弦定理  sinB sinC ， sin 4 asinB 2 10a asinC 3 5a b  c  可得  5 ，  5 ，····················································14分 sin sin 4 4 1 10a 又AC 的中点为D，所以CD  b ， 2 5 高三数学答案 第9页，共11页 {#{QQABLQAAogAgAgAAAQgCQQkwCgCQkhCCAQgOwFAIIAIAyBFABAA=}#}在ABC中，由余弦定理得：BD2 CD2 CB2 2CDCBcosC 10 10 10 ( a)2 a2 2 aa ······································································15分 5 5 10 a2 所以BD a，····································································································16分 10 所以cosCDB cosC  . 10 ························································································································ 17分 19．（本小题满分17分，其中第一小问4分，第二小问7分，第三小问6分。） 【解析】（1）因为  a  是12项01数列，当且仅当n3p(pN, p4)时，a 0， n n 所以当n3p2和n3p1(pN, p4)时，a 1. ··········································1分 n   设数列 (1)na 的所有项的和为S， n 则S (1)a (1)2a (1)4a (1)5a (1)7a (1)8a (1)10a (1)11a ······2分 1 2 4 5 7 8 10 11 (1)(1)2 (1)4 (1)5 (1)7 (1)8 (1)10 (1)11 (1)11(1)(1)11(1) 0   所以数列 (1)na 的所有项的和为0. ·····································································4分 n （2）①证明：因为数列  a  ，  b  是从集合M 中任意取出的两个数列， n n k 所以数列  a  ，  b  为k项01数列， n n 所以X 的可能取值为：1,2,3,,k . ········································································5分 因为集合M 中元素的个数共有C0 C1 C2 Ck 2k 个，····································6分 k k k k k 当X m(m1,2,,k)时，则数列  a  ，  b  中有m项取值不同，有km项取值相同， n n 高三数学答案 第10页，共11页 {#{QQABLQAAogAgAgAAAQgCQQkwCgCQkhCCAQgOwFAIIAIAyBFABAA=}#}Cm2k k 所以 A2 Cm , ····················································7分 P(X m) 2  k (m1,2,,k) C2 2k 1 2k 所以随机变量X 的分布列为： X 1 2 3 …… k C1 C2 C3 Ck P k k k …… k 2k 1 2k 1 2k 1 2k 1 ··························································································································8分 mk! (k1)! 因为mCm  k kCm1(mN,1mk)， k m!(km)! (m1)!  (k1)(m1)  ! k1 ··························································································································9分 C1 C2 Ck 1 所以E(X)1 k 2 k k k  (1C1 2C2 3C3 kCk) 2k 1 2k 1 2k 1 2k 1 k k k k k k2k1 k2k1 k  (C0 C1 C2 Ck1)   ， 2k 1 k1 k1 k1 k1 2k 1 2k 2 k 即E(X) . ··································································································11分 2     P(AB) P(AB) P(B)P(AB) ②解：由条件P B A P B A 得：   ，··················12分 P(A) P(A) 1P(A)     所以P(AB)1P(A)  P(A) P(B)P(AB) ， 化简得：P(AB) P(A)P(B)，·············································································14分 所以P(AB)P(B)P(AB) P(A)P(B)P(B)P(AB)，     则P(AB)1P(B)  P(B) P(A)P(AB) 即P  AB  P  B  P  B  P  AB  ，·········································································16分   所以 P  AB   P AB ，即P  A|B P  A|B  .     P B P B ························································································································ 17分 高三数学答案 第11页，共11页 {#{QQABLQAAogAgAgAAAQgCQQkwCgCQkhCCAQgOwFAIIAIAyBFABAA=}#}