文档内容
数学答案
1【答案】 .【详解】由 可得: ,所以 ,
由 可得: ,所以 , ,所以 , .故选: .
2【答案】 .【详解】 复数 满足 ,
, .故选: .
3【答案】 .【详解】 ,
,即 , 非负实数 , , , ,
,
当且仅当 时取等号, 的最小值为2.故选: .
4【答案】D【详解】由 得 ,因此可
知 方向相反,且 ,
对于A, ,由于 与 的关系不确定,故A错误,
对于B,由于 ,故B错误,
对于C, ,所以 ,故C错误,
对于D, ,故D正确,故选:D
5【答案】 .【详解】根据辅助角公式可知,,
由题意可知 ,
所以 ,
对于 项,当 时, , 正确;
对于 项,令 ,此时函
数 单调递增,故 正确;
对 于 项 , , , 则 当 时 ,
,此时 有两个零点,即
,
正确.
故选: .
6.【答案】 .【详解】由题意,令 ,则方程 的解
为1,
所以 ,解得 ,
故可得 ,显然当 时, ;
当 时, ;当 时, 或4.由题意可得 .故选: .
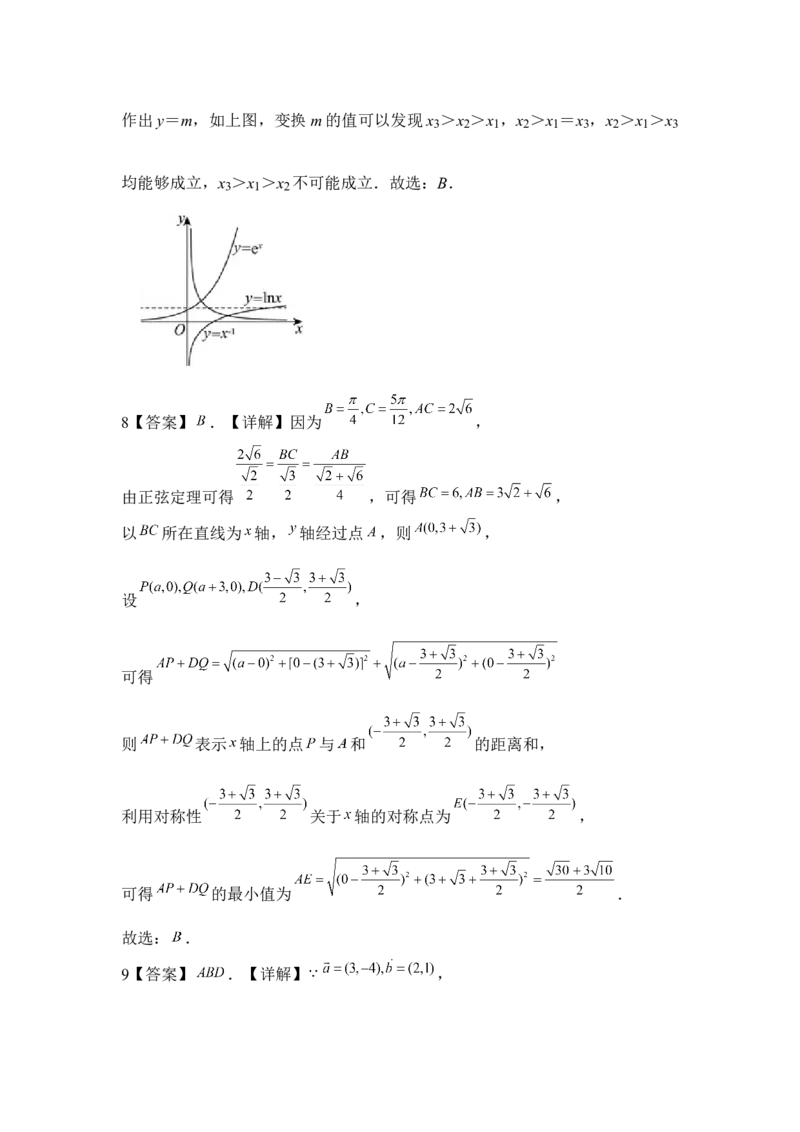
7【答案】B.【详解】因为 ,则 ,
由 ,得x >1,x >0,作函数 的图象,同时
2 3作出y=m,如上图,变换m的值可以发现x >x >x ,x >x =x ,x >x >x
3 2 1 2 1 3 2 1 3
均能够成立,x >x >x 不可能成立.故选:B.
3 1 2
8【答案】 .【详解】因为 ,
由正弦定理可得 ,可得 ,
以 所在直线为 轴, 轴经过点 ,则 ,
设 ,
可得
则 表示 轴上的点 与 和 的距离和,
利用对称性 关于 轴的对称点为 ,
可得 的最小值为 .
故选: .
9【答案】 .【详解】 ,, , ,与向量 平行的单位向量为
,向量 在 方向上的投影向量为 .
故选: .
10【答案】 .【详解】 .因为 ,所以
, ,又 ,所以 , 错;
.若 ,且 ,则 ,三角形有两解, 正确;
.若 为锐角三角形,则 , ,所以 ,
, , , 正确;
. 若 为 边 上 的 中 点 , 则 ,
,
又 , ,
, ,当且仅当 时
等号成立,
所以 ,所以 ,当且仅当
时等号成立, 正确.
故选: .11.【答案】 .【详解】由题意 得
,
由于 有两个不同的极值点 , ,
即 有2个正数根 , ,则 , ,
故需满足 ,解得 ,
对于 , , 错误;
对于 ,故 ,
令 , ,
即 在 上单调递减,故 ,
即 , 正确;
对于 ,
, 正 确 ; 对 于 ,
,
可看作曲线 上两点 , , , 连线的斜率,由于 ,故不妨设 , ,
由于 ,则曲线 在 处的切线斜率为1,
由于 , ,故 , , , 连线的斜率小于1,
即 ,所以 ,即 , 正确.
故选: .
12.【答案】 【详解】解:因为 且 ,
所以 ,
又因为 ,所以数列 是以 为首项,2为公差的等差数列,
所以
.
13.【答案】 【详解】已知 , 满足 , ,
则 ,
所以 ,
所以 .
2 2 2 2 2 2
14.【答案】8【详解】解:因为a +b +ab=c ,即a +b ﹣c =﹣ab ,
2 2 2
由余弦定理可得a +b +﹣c =2abcosC,所以cosC=﹣ ,而C (0, ),
∈ π
所以C= ,
因为 • =| |•| |cos( ﹣C)=﹣bacosC= ab,由S△ABC = absinC=
π(b+a)•CMsin ,即 ab= •2(a+b),
可得ab=2(a+b)≥2•2 ,当且仅当a=b时取等号,即ab≥16,
所以 • = ab≥ •16=8.即 • 的最小值为8.
15.【详解】(1)等差数列 的前 项和为 , ,
,
,-------------------------3分
解得 , ,----------------------6分
. 的通项公式为 .----------------------8分
(2) ,----------------------10分
数列 的前 项和为:
.--13
分
16 . 【 详 解 】 ( Ⅰ ) 因 为 , 由 正 弦 定 理 可 得
,2分
又 ,
所以 ,可得 ,------4
分
又 ,所以可得 ,又 ,所以 ;-----6分
(Ⅱ)因为 , ,由正弦定理 ,可得 , ,-----8分
又 ,所以 ,可得 ,-----10分
由 余 弦 定 理 , 可 得
,---13分
所以 .-----15分
17.【详解】(1)由已知得 ,则 ,又
,-----2分
所以 的图象在点 处的切线方程为 ,-----4分
将点(2,1)代入得 ,解得 .-----6分
(2)所以 ,定义域为 ,
所以 ,-----8分
令 ,则 ,
易得 在 上恒成立,所以 在 上单调递增,-----10分
又 ,所以当 时, ,即 , 在 上单调递减,
当 时, ,即 , 在 上单调递增,-----13分
所以 的极小值为 ,无极大值.-----15分
18.【详解】(1)因为 ,
由正弦定理得: ,-----2分所以 ,
因为 ,
所以 ,
即 ,
即 ,整理得 ,
因为 ,所以 ,所以 ,-----4分
即 ,所以 ,-----6分
因为 ,所以 ,可得 ;-----8分
(2)因为 , ,所以 的面积 ,-----10分
由正弦定理得 .-----12分
由于 为锐角三角形,故 , ,
因为 ,所以 ,----14分
可得 , ,可得 ,-----16分
从而 .因此, 面积的取值范围是 , .-----17分
19.【详解】(1)证明:设 ,-----2分
当x (0, )时, ,
∈ π
所以g(x)在(0, )上单调递减.-----4分
π又因为 ,
所以g(x)在 上有唯一的零点a,-----6分
即函数f′(x)在(0, )上存在唯一零点,
当x (0,a)时,f′(x)>0,f(x)在(0,a)上单调递增;
π
当x (a, )时,f′(x)<0,f(x)在(a, )上单调递减,
∈
所以f(x)在(0, )上存在唯一的极大值点a.-----8分
∈ π π
(2)①由(1)知:f(x)在(0, )上存在唯一的极大值点
π
π
,
所以 ,
又因为 ,
所以f(x)在(0,a)上恰有一个零点,-----10分
又因为f( )=ln ﹣ <2﹣ <0,
所以f(x)在(a, )上也恰有一个零点.-----12分
π π π π
②当x [ ,2 )时,则sinx≤0,f(x)≤lnx﹣x,
π
∈ π π
设 ,
所以h(x)在[ ,2 )上单调递减,所以h(x)≤h( )<0,
所以当x [ ,2 )时,f(x)≤h(x)≤h( )<0恒成立,
π π π
所以f(x)在[ ,2 )上没有零点.-----14分
∈ π π π
③当x [2 ,+∞)时,f(x)≤lnx﹣x+2,
π π
∈ π
设 ,
所以 (x)在[2 ,+∞)上单调递减,
所以 (x)≤ (2 )=ln2 ﹣2 +2<2﹣2 +2=4﹣2 <0,
φ π
所以当x [2 ,+∞)时,f(x)≤ (x)≤ (2 )<0恒成立,
φ φ π π π π π
所以f(x)在[2 ,+∞)上没有零点.-----16分
∈ π φ φ π
综上,f(x)有且仅有两个零点.-----17分
π