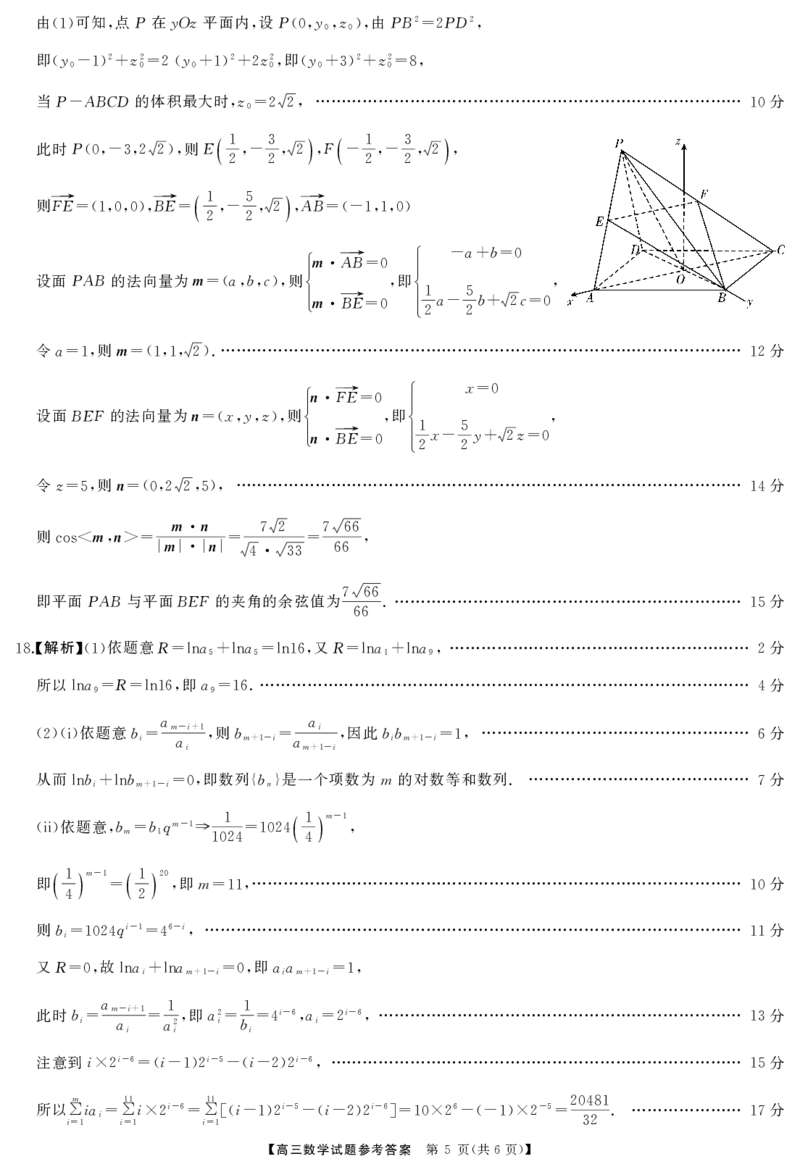文档内容
届高三 月联考数学
2025 10
参考答案、提示及评分细则
.【答案】
1 A
{m2
=1
【解析】因为A B A 所以 即得m .
={-1,1}, ⊆ , , =-1
m
=-1
.【答案】
2 D
【解析】当a b 时a2 b2 但是 a b 故a2 b2 a b
=-2,=1 , > , e<e, > /⇒e>e
当a b 时 a b 但是a2 b2 故 a b a2 b2
=1,=-2 ,e>e, < , e>e/⇒ >
故a2 b2 是 a b 的既不充分也不必要条件.
“ > ” “e>e”
.【答案】
3 C
【解析】由已知可得 a b a b 解得a .
-2= +i+ -i, =-1
.【答案】
4 C
θ π 2 θ 2 θ
cos(+ ) cos- sin θ
【解析】依题意有 θ 且 θ 4 2 2 1-tan
tan >0, tan = = = θ,
cos( θ - π ) 2 cos θ + 2 sin θ 1+tan
4 2 2
故 2θ θ 结合 θ 解得 θ .
tan +2tan -1=0, tan >0, tan = 2-1
.【答案】
5 B
【解析】因为fx 在R上单调递增 所以当x y x2 ax单调递增 所以a
() , <0,=- + , ≥0,
当x 时f′x x a 由fx 单调递增可知a
≥0 , ()=e- ≥0, () ≤1,
且当x f 所以a的取值范围是 .故选 .
=0,0≤ (0)=1, [0,1] :B
.【答案】
6 C
【解析】设Pxy 则PA2 PB2 PC2 x 2 y 2 x 2 y 2 x 2 y 2
(,), + + =( +1)+( -1)+( -1)+( +1)+( -3)+( -3)=
x2 y2 x y 故Pxy 的轨迹方程为x 2 y 2 .
3( + -2 -2 )+22=70, (,) (-1)+(-1)=18
PA→ PB→ PO→ 2 OA→ 2 PO→ 2 而 PO 故PA→ PB→ 选 .
= - = -2, ≤32+ 2=42, ≤30, C
.【答案】
7 B
【解析】对于 令x 则f 有 个函数值对应 故 错误
A, =±1, (e)=±1, 2 , A ;
对于 取x 可知fx2 x f 再取x 可知fx2 x f 故 错误
C, =0, ( +2 )= (0)=0, =-2, ( +2 )= (0)=2, C ;
对于 取x π 5πf 2 故 错误
D, = , ,(0)=± , D ;
4 4 2
高三数学试题参考答案 第 页 共 页
【 1 ( 6 )】
{#{QQABIQIAogCIQAAAAQgCUQVwCAMQkgGCAQgOBAAEoAAAyRNABAA=}#}对于 选项 令t xx 对于每一个t都有唯一的x与之对应 也即有唯一的x3 与之对应 因此符合函数
B , = ||, , , +1 ,
定义 故 正确.
, B
.【答案】
8 A
【解析】不妨设P在第一象限 设PAPB的倾斜角分别为αβ 则 β α APB 2
, , ,, tan(- )=tan∠ =
2
故tan β -tan α 2 注意到 α β y P y P y2P 1
1+tan
α
tan
β=
2
, tantan =x
P -32
x
P +32
=x2P
-18
=
2
,
因此 β α 2 α β 32 解得 α 2 β
tan -tan = (1+tantan )= , tan = ,tan = 2,
2 4 4
y y
故
x
P
=
2
, x
P
= 2,
代入解得
:
x
=52,
yP
=4
P +32 4 P -32
故
△
PAB的面积为S
=
1
|
AB
||
yP
|=122
.
2
.【答案】
9 ABD
【解析】对于 选项f x fx 正确
A ,(- )=- (), ;
对于 选项f′x x2 a fx 单调递增 正确
B , ()=3 - >0,() , ;
对于 选项f′x 恰有一个解 则a 但此时fx 无极值点 故 错误
C , ()=0 , =0, () , C ;
对于 选项fx xx a x a 存在三个零点 a a 故 正确.
D ,()= (+ )(- ), 0, ,- , D
.【答案】
10 ACD
【解析】对于 A,B 选项 , 根据通项公式 , a m a n = a 1 qm -1a 1 qn -1 = a2 1 qm + n -2 = a p2 = a2 1 q2 p -2 ,
故 A 正确 ; 若q =1, 则a m a n = a p2 恒成立 , 故 B 错误 ;
对于 由T T 不妨设m n 则a a a 则a a .
C,D, m = n, < , m +1 m +2 n =1, m +1 n =1
而T2m
+ n =(
a
1
a
m + n)(
a
2
a
m + n -1)(
a
3
a
m + n -2)(
a
m + n
a
1)=1,
可知T
m + n =1,
反之也成立 故 均正确.
, C,D
.【答案】
11 AC
【解析】对于 选项 如图 连接PAPB 由α β 可知 APA BPE 故PA PB 以A点为原点 AB
A , 1, , , = , ∠ 1=∠ , =2 , ,
为x轴 AD为y轴建系 Bb 设Pxy 则x2 y2 x b2 y2 即 x2 y2 bx b2 故P
, , (,0), (,), + =4(- )+4 , 3 +3 -8 +4 =0,
点的轨迹为圆 正确
,A ;
RT
对于 选项 如图 作PT AD于TTR AD 于R 则 γ 同理作PM CD于M MN CD
B , 2, ⊥ , ⊥ 1 1 , tan =PT, ⊥ , ⊥ 1 1
MN
于N 则 θ 由γ θ可知 PT PM 故P为 ADC的平分线 点P的轨迹为直线 错误
, tan =PM, = , = , ∠ , ,B ;
高三数学试题参考答案 第 页 共 页
【 2 ( 6 )】
{#{QQABIQIAogCIQAAAAQgCUQVwCAMQkgGCAQgOBAAEoAAAyRNABAA=}#}AA MN
对于 选项 如图 α 1 θ 由α θ可知 PM PA 根据抛物线的定义可知点P的轨迹为
C , 3,tan =PA,tan =PM, = , = ,
抛物线 正确
,C ;
对于 选项 由 选项可知PM PB 显然不是直线 错误.
D , C =2 , ,D
.【答案】 13
12 -
8
【解析】λa b λ λ 由 a b b 得 λ λ 解得λ 13.
+ =(+2,2 +3), (2 + ) =0, 2(+2)+3(2 +3)=0, =-
8
.【答案】
13 [4,+∞)
y a2 a2 a
【解析】x 4 x 4 x 4 a 故 a 即a .
+x+xy≥ +2 x2 = +x≥4 , 4 ≥8, ≥4
.【答案】2π
14
3
【解析】考虑fx 的周期为 不妨设x
() π, ∈[0,π],
f′x 2x x x x x 2x x 2x 2x x
()=2cos cos2 -2sincos sin2 =2cos (cos2 -2sin )=2cos (2cos2 -1)
é ù
令f′x 即 x 1 解得x ê êπ 5π ú ú 故b a 2π.
()≤0, cos2 ≤ , ∈ë , û, - ≤
2 6 6 3
.【解析】 因为 B C 所以 b c 分
15 (1) 2sin = 3sin , 2 = 3 , 2
又b2 c2 a2 所以b ac a 分
+ =5 , = 3 ,= 2 , 4
b2 c2 a2 a2 a2
从而 A + - 5 - 6. 分
cos = bc = a a= 6
2 23 2 3
由余弦定理可知b2 c2 bc A a2 则bc A a2 分
(2) + -2 cos = , cos =2 , 7
又AB→ AC→ bc A 故a 分
= cos =8, =2, 8
即b2 c2 故 bc 即bc 分
+ =20, 2 ≤20, ≤10, 10
从而S △ ABC = 1bc sin A = 1 b2c2 -( bc cos A ) 2 = 1 b2c2 -64≤3, 12 分
2 2 2
当b c 时取等号 即 ABC的面积的最大值为 . 分
= = 10 , △ 3 13
( )
.【解析】 法一 由PA PO可得P 3 设直线ly kx 3 分
16 (1) : 2= 1, , := (-1)+ , 1
2 2
高三数学试题参考答案 第 页 共 页
【 3 ( 6 )】
{#{QQABIQIAogCIQAAAAQgCUQVwCAMQkgGCAQgOBAAEoAAAyRNABAA=}#}( )
联立椭圆方程 x2 y2 得 x2 kx k 3 2
3 +4 =12 3 +4 - + =12,
2
即 k2x2 k x k 2 . 分
(3+4 ) -(8 -12)+(2 -3)-12=0 3
由 k 2 k2 k 2 解得k 1 分
Δ=(8 -12)-4(3+4 )[(2 -3)-12]=0, =- , 6
2
因此直线l的方程为y 1x . 分
:=- +2 7
2
x
法二 x2 y2 则y 1 x2 y′ 1 -3 令x 则y′ 1 分
:3 +4 =12, =
2
12-3 , =
2
12-3
x2 , =1, =-
2
, 5
故直线l的方程为y 1x 分
:=- +2, 7
2
依题意 直线MN的方程为y 1x 联立椭圆 x2 y2 可得x2 即x
(2) , =- , 3 +4 =12 =3, =± 3,
2
( ) ( ) ( )
即M 3 N 3 P 3 A . 分
- 3, , 3,- , 1, ,1(-2,0) 9
2 2 2
设圆的方程为x2 y2 Dx Ey F 代入A P M 可得
+ + + + =0, 1, , :
ì
ì ï ï D 1
13 D 3E F ï =
ï + + + =0 ï 8
ï 4 2
ï
ï ï
í D F 解得íE 1 分
ï 4-2 + =0 , ï = , 13
4
ï ï
ï ï
ï15 D 3E F
î - 3 + + =0 ïïF 15
4 2 î =-
4
此时圆方程为x2 y2 1x 1y 15 因为点N也在此圆上 所以P M A N四点共圆
+ + + - =0, , , ,1, ,
8 4 4
( ) ( )
其标准方程为 x 1 2 y 1 2 965. 分
+ + + = 15
16 8 256
.【解析】证明 设AC BD OOP EF Q 过点D作DH BQ于H
17 :(1) ∩ = , ∩ = , ⊥ ,
由面PBD 面BEF 且面PBD 面BEF BQ 故DH 面BEF
⊥ , ∩ = , ⊥ ,
即DH EF 分
⊥ ; 2
因为EF分别为PAPC的中点 因此EF AC 因此DH AC. 分
, , , ∥ , ⊥ 4
由底面ABCD为正方形可知AC BD 因此AC 面PBD 分
⊥ , ⊥ 5
由PO 面PBD 故AC PO
⊂ , ⊥ ,
因为O为AC的中点 因此PA PC 分
, = ; 6
不妨设AB 以O为坐标原点 OA为x轴 OB为y轴建立空间直角坐标系 则A B
(2) = 2, , , , (1,0,0), (0,1,0),
C D 分
(-1,0,0), (0,-1,0), 7
高三数学试题参考答案 第 页 共 页
【 4 ( 6 )】
{#{QQABIQIAogCIQAAAAQgCUQVwCAMQkgGCAQgOBAAEoAAAyRNABAA=}#}由 可知 点P在yOz平面内 设P y z 由PB2 PD2
(1) , , (0,0,0), =2 ,
即y 2 z2 y 2 z2 即y 2 z2
(0-1)+ 0=2(0+1)+20, (0+3)+ 0=8,
当P ABCD的体积最大时z 分
- ,0=22, 10
( ) ( )
此时P 则E 1 3 F 1 3
(0,-3,22), ,- ,2 , - ,- ,2 ,
2 2 2 2
( )
则FE→ BE→ 1 5 AB→
=(1,0,0), = ,- ,2 , =(-1,1,0)
2 2
ì ì ï a b
ï ï m AB→ =0 ï - + =0
设面PAB的法向量为m abc 则í 即í
=(,,), ïï , ï ,
îm BE→ =0 î ï1a - 5b + 2 c =0
2 2
令a 则m . 分
=1, =(1,1,2) 12
ì ì ï x
ï ï n FE→ =0 ï =0
设面BEF的法向量为n xyz 则í 即í
=(,,), ïï , ï ,
în BE→ =0 î ï1x - 5y + 2 z =0
2 2
令z 则n 分
=5, =(0,22,5), 14
m n
则 mn 72 7 66
cos< ,>= m n = = ,
| ||| 4 33 66
即平面PAB与平面BEF的夹角的余弦值为7 66. 分
15
66
.【解析】 依题意R a a 又R a a 分
18 (1) =ln5+ln5=ln16, =ln1+ln9, 2
所以 a R 即a . 分
ln9= =ln16, 9=16 4
a a
依题意b m - i +1 则b i 因此bb 分
(2)(i) i = a i , m +1- i =a m i , i m +1- i =1, 6
+1-
从而 b b 即数列b 是一个项数为m的对数等和数列. 分
ln i +ln m +1- i =0, {n} 7
( )m
(ii) 依题意 , b m = b 1 qm -1 ⇒ 1 =1024 1 -1 ,
1024 4
( )m ( )
即 1 -1 1 20 即m 分
= , =11, 10
4 2
则b
i =1024
qi
-1 =4 6-
i
, 11
分
又R 故 a a 即aa
=0, ln i +ln m +1- i =0, i m +1- i =1,
a
此时b i = m a - i i +1 =a 1 i2 , 即a i2 =b 1 i=4 i -6 , a i =2 i -6 , 13 分
注意到i i -6 i i -5 i i -6 分
×2 =(-1)2 -(-2)2 , 15
m
所以 i∑ ia i =i∑ 11 i ×2 i -6 =i∑ 11 [( i -1)2 i -5 -( i -2)2 i -6 ]=10×2 6 -(-1)×2 -5 = 20481. 17 分
=1 =1 =1 32
高三数学试题参考答案 第 页 共 页
【 5 ( 6 )】
{#{QQABIQIAogCIQAAAAQgCUQVwCAMQkgGCAQgOBAAEoAAAyRNABAA=}#}( )
.【解析】 依题意fx x xf′x x x 1 分
19 (1) ()=eln , ()=e ln +x , 1
x
设px x 1 则p′x 1 1 -1 分
()=ln +x, ()=x-x2= x2 , 2
当 x 时px 单调递减 当x 时px 单调递增
0< <1 ,() , >1 ,() ,
故px p 即f′x fx 单调递增. 分
()≥ (1)=1>0, ()>0,() 4
设a tt 则fx 1tx x
(2)(i) =e(≠0), ()=teln ,
tx tx( )
则f′x tx x e e x x 1 . 分
()=eln +tx=x ln +t 5
( ) ( )
设gx x x 则g′x x 即gx 在 1 上单减 在 1 上单增 分
()= ln , ()=1+ln , () 0, , ,+∞ , 6
e e
当t 时 令gx 1 由g 且gx 在 上单调递增
<0 , ()=-t, (1)=0, () (1,+∞) ,
故gx 1仅有一个零点x 不符合题意 分
()=-t 0, ; 7
é ö
当t 时gx ê ê 1 ÷
>0 ,()∈ë- ,+∞ø,
e
当t 时 则 1 1 此时gx 1f′x
① ≤e , -t≤- , ()≥-t, ()≥0,
e
fx 单调递增 不符合题意 分
() , ; 8
当t 时 则 1 1 此时gx 1存在两个零点x x
② >e , - <-t<0, ()=-t 1< 2,
e
当x x 时gx 1f′x 当x x x 时gx 1f′x
∈(0,1) ()>-t, ()>0; ∈(1,2) ,()<-t, ()<0;
当x x 时gx 1f′x fx 存在两个极值点 符合题意.
∈(2,+∞) ,()>-t, ()>0,() ,
综上可知a e . 分
,∈(e,+∞) 10
( )
由 可知M fx 且x 1 满足x x 1
(ii) (i) = (1), 1∈ 0, , 1ln 1=-t,
e
故M = f ( x 1)=t 1 e tx 1 ln x 1=- x 1(ln x 1) 2 e -ln x1 1, 12 分
设r x 则M r1 - rr2 2ln r - r +r1 分
=-ln 1∈(1,+∞), =-e =-e , 14
r 2
设hr r r 1 则h′r 2 1 (-1) 分
()=2ln - +r, ()=r-1-r2=- r2 <0, 16
故hr 单调递减 且h 则hr
() , (1)=0, ()∈(-∞,0),
即M 2ln r - r +r1 . 分
=-e ∈(-1,0) 17
高三数学试题参考答案 第 页 共 页
【 6 ( 6 )】
{#{QQABIQIAogCIQAAAAQgCUQVwCAMQkgGCAQgOBAAEoAAAyRNABAA=}#}