文档内容
河南省信阳高级中学新校(贤岭校区)
2025-2026 学年高二上期 11 月测试(一)
数学答案(物理方向)
题号 1 2 3 4 5 6 7 8 9 10 11
答案 D A D C C D A B AB BD BC
13.2
12. 14.
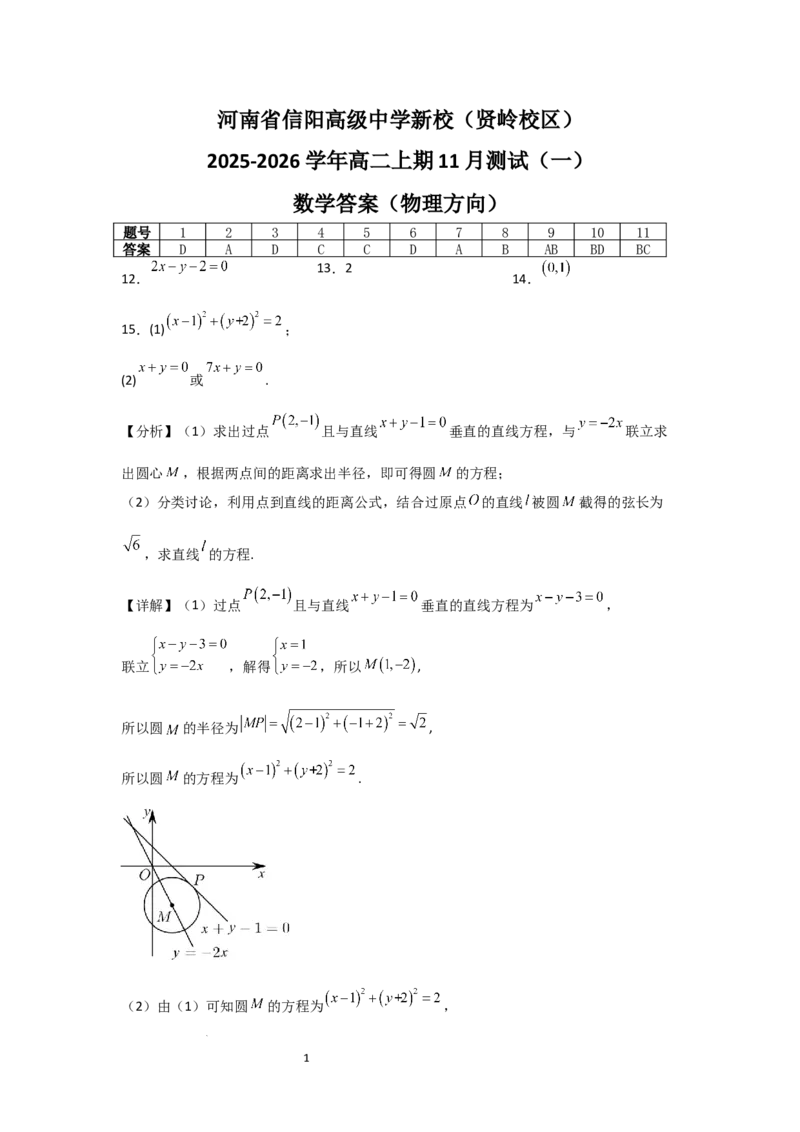
15.(1) ;
(2) 或 .
【分析】(1)求出过点 且与直线 垂直的直线方程,与 联立求
出圆心 ,根据两点间的距离求出半径,即可得圆 的方程;
(2)分类讨论,利用点到直线的距离公式,结合过原点 的直线 被圆 截得的弦长为
,求直线 的方程.
【详解】(1)过点 且与直线 垂直的直线方程为 ,
联立 ,解得 ,所以 ,
所以圆 的半径为 ,
所以圆 的方程为 .
(2)由(1)可知圆 的方程为 ,
1
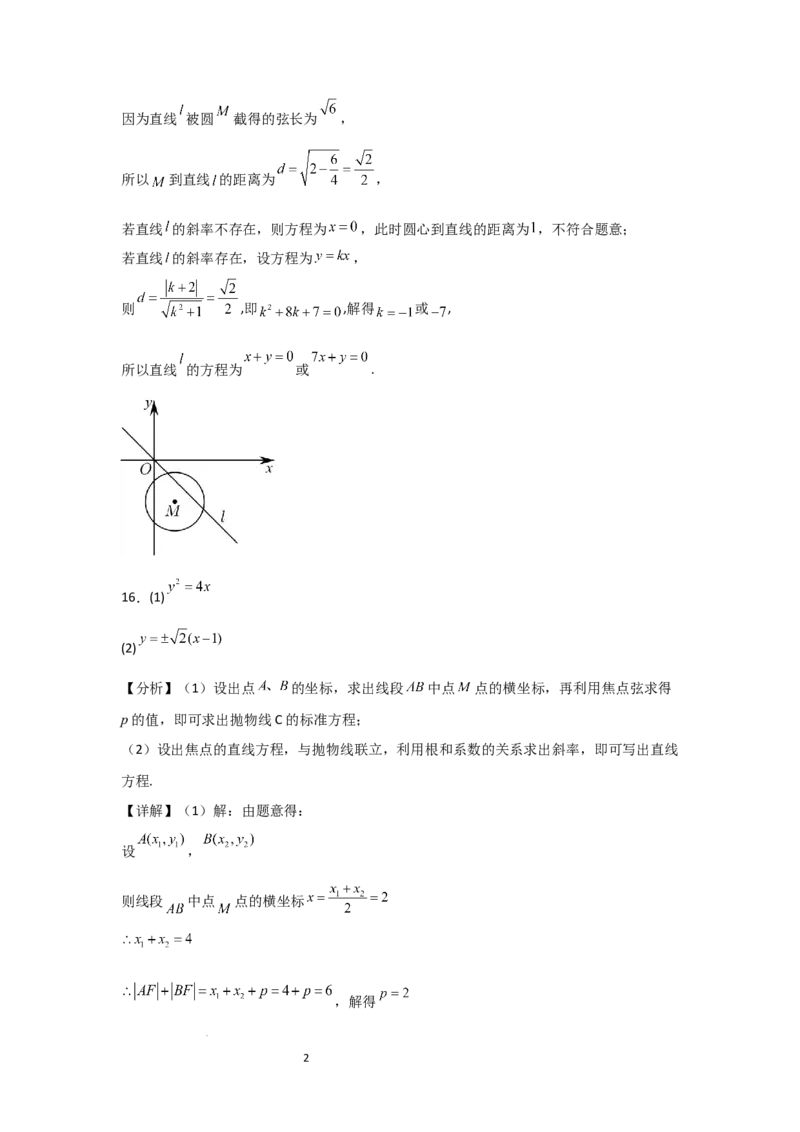
学科网(北京)股份有限公司因为直线 被圆 截得的弦长为 ,
所以 到直线 的距离为 ,
若直线 的斜率不存在,则方程为 ,此时圆心到直线的距离为 ,不符合题意;
若直线 的斜率存在,设方程为 ,
则 ,即 ,解得 或 ,
所以直线 的方程为 或 .
16.(1)
(2)
【分析】(1)设出点 的坐标,求出线段 中点 点的横坐标,再利用焦点弦求得
p的值,即可求出抛物线C的标准方程;
(2)设出焦点的直线方程,与抛物线联立,利用根和系数的关系求出斜率,即可写出直线
方程.
【详解】(1)解:由题意得:
设 ,
则线段 中点 点的横坐标
,解得
2
学科网(北京)股份有限公司抛物线的标准方程为 .
(2)由问题(1)可知抛物线的焦点坐标为
故设直线方程为
联立方程组为
解得
直线l的方程
17.(1)证明见解析
(2)
(3)
【分析】(1)根据已知条件将向量 用向量 表示出来得出 即可证
明结论;
(2)利用向量的线性表示将向量 用向量 表示出来即可解决问题;
(3)利用向量数量积,先把向量 用向量 表示出来,然后利用向量法求模即
可.
【详解】(1)因为 ,
所以 ,
,
所以 ,
3
学科网(北京)股份有限公司所以四边形 是平行四边形.
(2)由(1)知 ,
,
所以 ,
由 ,
所以 , , , .
(3)因为四边形 是正方形,
所以 ,
因为 , , ,
所以 ,
易知在四棱柱 中,
,
所以
.
18.(1) ;(2) .
19.(1)证明见解析
(2)证明见解析
【分析】(1)设直线 代入 ,设 ,由韦达定理得
4
学科网(北京)股份有限公司,设 ,求出 ,由 得
,故 ,代入求得 关系,然后计算 的面积为可得;
(2)先证明 和 的中点重合,再结合三角形的面积关系可证.
【详解】(1)设直线 代入 得 ,
由 得 ,
设 ,则有 ,
设 ,易得 ,
由 得 ,
故 ,
代入得 ,整理得: ,
又 ,
为定值.
(2)设 中点为 中点为
5
学科网(北京)股份有限公司则 , ,所以 , 重合,
从而 ,从而 ,又 的面积等于 面积的 ,
所以 ,从而 .
6
学科网(北京)股份有限公司