文档内容
精讲精练-资料 7
(笔记)
主讲教师:邓健
授课时间:2025.03.08
粉笔公考·官方微信
更多资料公众号:考公小镇精讲精练-资料 7(笔记)
第八节特殊增长率
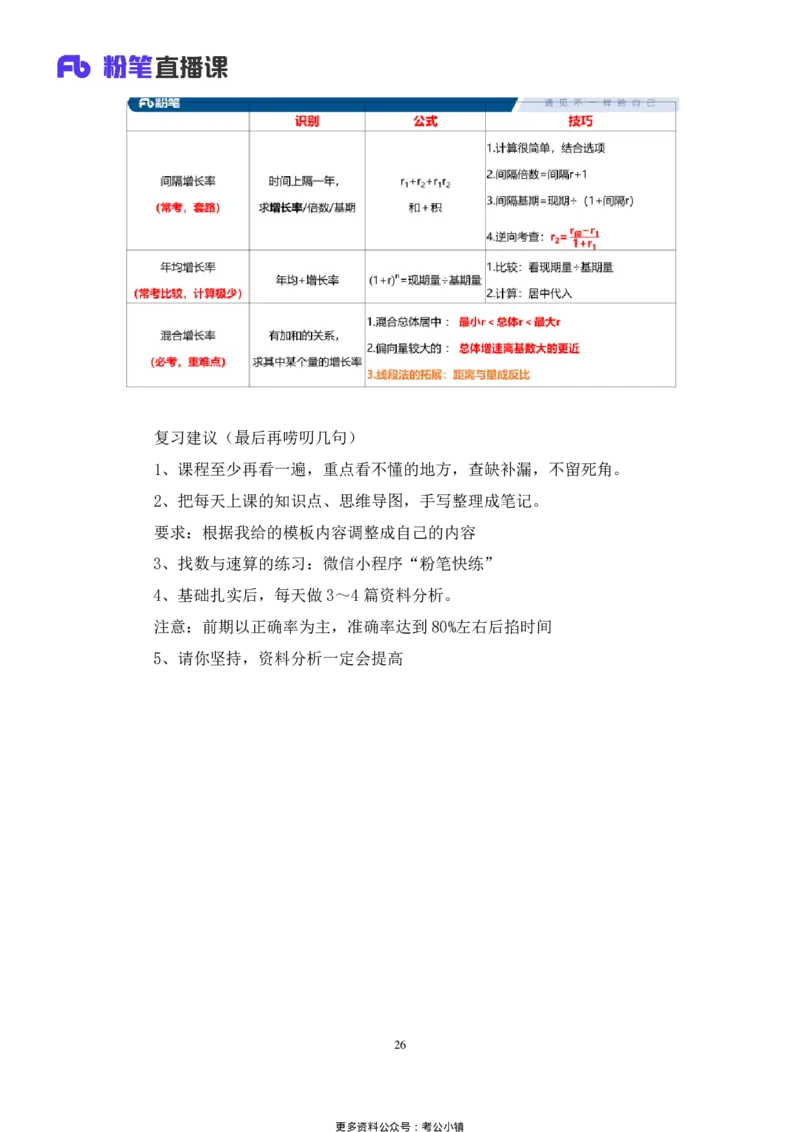
间隔增长率(常考,简单、套路)
年均增长率(常考比较,计算几乎不考)
混合增长率(必考重点,技巧性强)
【注意】特殊增长率:
1.间隔增长率(常考,简单、套路)。
2.年均增长率(常考比较,计算几乎不考,感觉挺难,但其实简单)。
3.混合增长率(必考重点,技巧性强)。
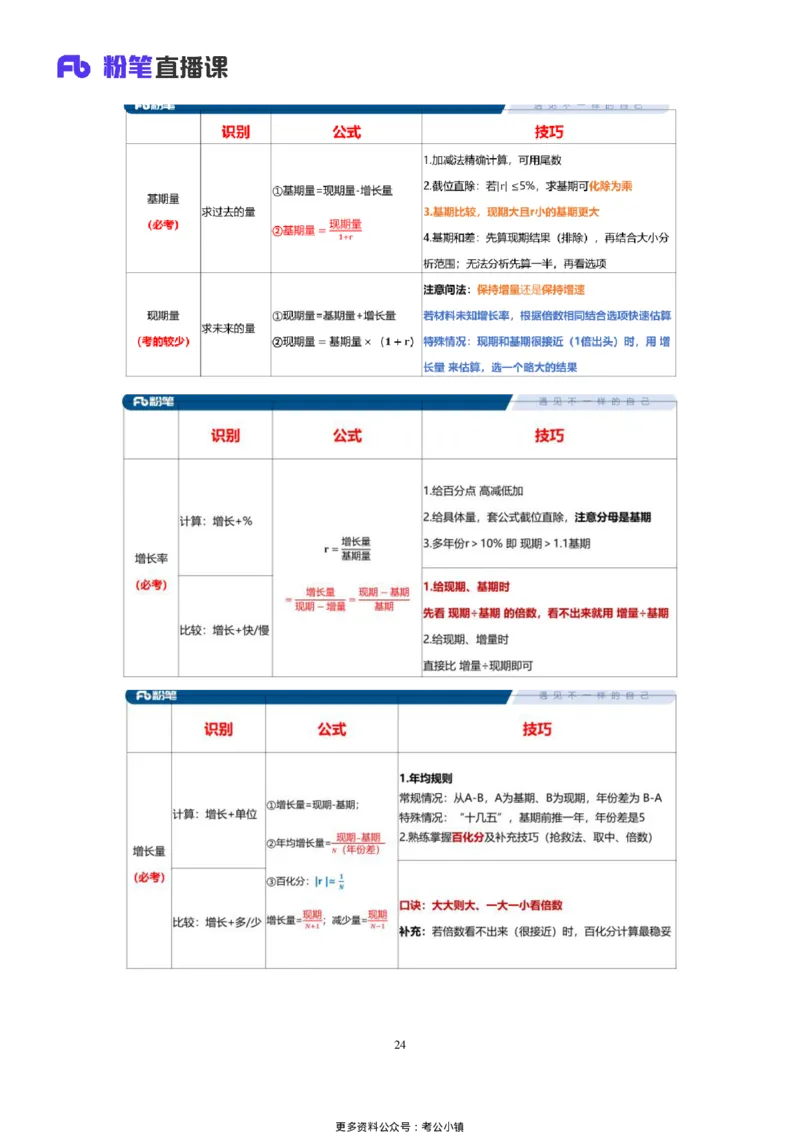
一、间隔增长率
识别:2020年比 2018年增长+%(隔一年,求增长率)
已知:2020年收入同比增长率为 r,2019 年同比增长率为r
1 2
求:2020年与 2018年相比的增长率是多少?
现期=基期*(1+r)
2020年=2019年*(1+r)=2018年*(1+r)*(1+r)
1 2 1
r=(现期- 基期)基期=(2020年-2018 年)/2018年
r =r+r+r*r
间隔 1 2 1 2
r:今年的增长率
1
r:去年的增长率
2
【注意】间隔增长率
1.识别:2020 年比2018年增长+%(隔一年,求增长率)。
2.已知:2020 年收入同比增长率为 r,2019 年同比增长率为 r 。求:2020
1 2
年与2018年相比的增长率是多少?
1
更多资料公众号:考公小镇(1)求增长率,r=(现期- 基期)基期=(2020年-2018年)/2018 年,材
料不会直接给出2018 年数据,考虑用“现期=基期*(1+r)”将 r、r 联系起来,
1 2
2020年=2019年*(1+r)=2018年*(1+r)*(1+r),代回原始公式,[2018年
1 2 1
*(1+r1)*(1+r2)-1]/2018年=1+r+r+r *r-1=r+r+r*r。
1 2 1 2 1 2 1 2
(2)r:今年(2020年)的增长率;r :去年(2019年)的增长率。
1 2
3.通过“笑脸”图形象记忆,已知 2020 年比 2019 年的增长率 r、2019 年
1
比 2018 年的增长率 r ,可以求出 2020 年比 2018 年的增长率 r ,记忆为“和+
2 间
积”。
速算技巧:r=r +r+r*r
1 2 1 2
1.先计算r+r ,结合选项
1 2
【练习1】8.5%+36%+8.5%*36%≈( )
A.47.6% B.40.4%
C.34.5% D.27.6%
2.若r、r 的绝对值均小于 10%(r*r<1%),结合选项乘积可忽略
1 2 1 2
【练习2】5.6%+6.3%+5.6%*6.3%≈( )
A.12.26% B.10.87%
C.13.21% D.9.69%
3.结合选项不能排除:挑一个百化分
【练习3】11.9%+25.1%+11.9%*25.1%≈( )
A.38.8% B.39.9%
C.37.7% D.36.6%
【注意】速算技巧:r=r+r+r*r。
1 2 1 2
1.先计算r+r ,结合选项。
1 2
例:8.5%+36%+8.5%*36%≈( )。
A.47.6% B.40.4%
C.34.5% D.27.6%
答:8.5%+36%=44.5%,8.5%*36%为正数,答案比44.5%大,对应 A项。
2.若r、r 的绝对值均小于 10%(r*r<1%),结合选项乘积可忽略。
1 2 1 2
2
更多资料公众号:考公小镇例:5.6%+6.3%+5.6%*6.3%≈( )。
A.12.26% B.10.87%
C.13.21% D.9.69%
答:5.6%+6.3%=11.9%,5.6%*6.3%为正数,答案比11.9%大,锁定 A、C项。
5.6%*6.3%<10%*10%=1%,对结果的影响很小,一般可以忽略,所求=11.9%+1-%,
对应A项。
3.结合选项不能排除:挑一个百化分。比如 63%*14.3%≈63%*(1/7)=9%。
例:11.9%+25.1%+11.9%*25.1%≈( )。
A.38.8% B.39.9%
C.37.7% D.36.6%
答:11.6%+25.4%=37%,11.9%*25.1%为正数,答案比 37%大,但选项均满足。
11.9%*25.1%≈12%*(1/4)=3%,所求=37%+3%=40%,对应B项。
一、间隔增长率
识别:中间隔一年,求增长率
公式:r=r+r+r *r(和+积)
1 2 1 2
计算:①先算加法,结合选项排除
②再算乘法:若 r、r 均小于10%,则乘积小于1%,一般可忽略
1 2
有超过10%,可百化分快速计算
【注意】间隔增长率:
1.识别:中间隔一年(比如 2020年比2018 年,2016年比2014 年,如果隔
好几年的数据,则不是间隔增长率的知识点,而是年均增长率相关问题),求增
长率。
2.公式:r=r+r +r*r(和+积)。
1 2 1 2
3.计算:
(1)先算加法,结合选项排除。
(2)再算乘法:
①若r、r 均小于 10%,则乘积小于 1%,一般可忽略。
1 2
②有超过10%,可以将其中一个化为 1/n 的形式计算。
3
更多资料公众号:考公小镇【例1】(2024 四川)2022 年,全国软件和信息技术服务业规模以上企业超
3.5万家,累计完成软件业务收入 108126亿元,同比增长 11.2%,增速较上年同
期回落6.5个百分点。
2022 年,全国软件和信息技术服务业规模以上企业累计完成软件业务收入
约比2020年增长了:
A.16% B.23%
C.29% D.31%
【解析】1.增长+%,2022 年与 2020年间隔一年,求增长率,间隔增长率问
题,公式:r=r+r+r *r。主体为“国软件和信息技术服务业规模以上企业累计
1 2 1 2
完成软件业务收入”,已知“累计完成软件业务收入108126亿元,同比增长11.2%,
增速较上年同期回落 6.5 个百分点”,给出增长率和百分点,则 r=11.2%,高减
1
低加,r=11.2%+6.5%=17.7%。代入数据,所求=11.2%+17.7%+11.2%*17.7%>28.9%,
2
增长率均大于 10%,不能忽略,11.2%*17.7%>1%,所求=28.9%+1+%>30%,对应
D项。【选D】
【注意】如果计算:11.2%*17.7%≈1/9*18%=2%,所求=28.9%+2%=30.9%,对
应D项。
【例 2】(2024 联考)2022 年,全国共有 260 家银行机构和 29 家理财公司
累计新发理财产品 2.94 万只,同比下降 38.23%,降幅比上年同期扩大 7.22 个
百分点;累计募集资金 89.62万亿元,同比减少 32.57万亿元。
2022 年全国银行机构和理财公司累计新发理财产品只数与 2020 年相比约:
A.下降45% B.下降 57%
C.下降66% D.下降 69%
【解析】2.下降+%,求增长率,2022年与 2020 年隔一年,间隔增长率问题,
公式:r间=r+r+r *r。主体为“全国银行机构和理财公司累计新发理财产品只
1 2 1 2
数”,已知“2022 年,全国共有 260 家银行机构和 29 家理财公司累计新发理财
产品2.94万只,同比下降 38.23%,降幅比上年同期扩大 7.22个百分点”,给出
4
更更多多资资料料公公众众号号::考考公公小小镇镇增长率和百分点,r =-38.23%,高减低加,r =-(38.23%-7.22%)≈-31%,代入数
1 2
据,所求=-38.23%-31%+38.23%*31%,|r|均大于 10%,不能忽略,所求≈-69%+38%*
(1/3)≈-69%+12%=57%,对应B项。【选B】
【注意】降幅的变化分析:先对降幅的高减低加,求增长率补上负号。比如
老邓亏了5万,亏损比去年扩大了 2万,则去年亏算了 3万。高减低加,去年亏
损=5-2=3万,利润=-3万。
题型延伸①:间隔倍数
特征:隔一年,求倍数
2020年工资同比增长了 25%,2019年同比增长了 20%
则2020年工资是 2018年的多少倍?
两步走:
①先求出间隔增长率
②间隔倍数=间隔增长率+1
【注意】间隔倍数:
1.特征:隔一年,求倍数。比如今年比去年的增长率为 35%,则今年是去年
的1.35倍(倍数=r+1)。
2.两步走:
(1)先求出间隔增长率。
(2)间隔倍数=间隔增长率+1。
3.例:2020 年工资同比增长了 25%,2019 年同比增长了 20%,则 2020 年工
资是2018年的多少倍?
答:问 2020 年是 2018 年的多少倍,先求间隔增长率,再“+1”,r=25%、
1
r=20%,r =25%+20%+25%*20%=45%+25%*(1/5)=45%+5%=50%,间隔增长率 50%,
2 间
则间隔倍数为1.5倍。
题型延伸②:间隔基期量
特征:隔一年,求基期
5
更更多多资资料料公公众众号号::考考公公小小镇镇2020年工资额是 400元,同比增长了10%,2019年同比增长了 20%
则2018年的工资是多少元?
两步走:
①先求出间隔增长率
②间隔基期=现期量/(1+间隔增长率)
【注意】间隔基期量:
1.特征:隔一年,求基期。
2.计算方法:两步走。
(1)先求出间隔增长率。
(2)间隔基期=现期量/(1+间隔增长率)。
3.例:2020 年工资额是 400 元,同比增长了 10%,2019 年同比增长了 20%,
则2018年的工资是多少元?
(1)常规思路:2020年/(1+10%)=400/(1+10%)=2019年,2019年/(1+20%)
=2018年。
(2)先算出间隔增长率,基期=现期/(1+间隔增长率)。r
间
=10%+20%+10%*20%=32%,所求=400/(1+32%)=400/1.32≈300。
【例3】(2024 联考)2023 年,全国软件和信息技术服务业规模以上企业超
3.8万家,累计完成软件业务收入 123258亿元,同比增长 13.4%,较上年同期增
长2.2个百分点。
2021年,全国软件和信息技术服务业规模以上企业的软件业务收入约为:
A.不到9万亿元 B.9 万亿~10万亿元
C.10万亿~11 万亿元 D.11 万亿元以上
【解析】3.间隔一年求基期,先求间隔增长率。主体为“全国软件和信息技
术服务业规模以上企业的软件业务收入”,已知“同比增长13.4%,较上年同期增
长2.2个百分点”,给出增长率、百分点,r =13.4%,高减低加,则 r=13.4%-2.
1 2
2%=11.2%,r =r+r +r*r=13.4%+11.2%+13.4%*11.2%=24.6%+1+%≈26%,间隔基
间 1 2 1 2
期=现期/(1+间隔增长率)≈12.3 万亿/(1+26%)=12.3/1.26=10-,对应 B 项。
【选B】
6
更更多多资资料料公公众众号号::考考公公小小镇镇题型延伸③:间隔增长率逆向公式
常规情况:给 r 和r,求r
1 2 间隔
逆向考查:给 r 和r ,求 r
1 间隔 2
r =r+r+r*r
间隔 1 2 1 2
r=(r -r)/(1+r)
2 间 1 1
【引例】已知2021 年比2020 年增长15%,2021比2019年增长30%,求 2020
比2019年增长大约多少?
A.-16% B.-13%
C.13% D.16%
【注意】题型延伸③:间隔增长率逆向公式。
1.常规情况:给 r 和r,求 r 。
1 2 间隔
2.逆向考查:给 r 和r ,求r。三个量知道其中两个,一定能求出第三个
1 间隔 2
量。
3.公式推导:r =r+r+r*r →r -r=r *(1+r)→r=(r -r)/(1+r )。
间隔 1 2 1 2 间 1 2 1 2 间 1 1
4.引例:已知2021 年比2020 年增长15%,2021比2019年增长30%,求 2020
比2019年增长大约多少?
A.-16% B.-13%
C.13% D.16%
答:给r 、r,求 r,代入数据,所求=(30%-15%)/(1+15%)=15%/(1+)
间 1 2
<15%,对应C项。
【例 4】(2023 国考)2021 年,全国纺织品服装出口 3155 亿美元,同比增
长 8.4%。其中,纺织品出口 1452.2 亿美元,同比下降 5.6%,较 2019 年增长
22.0%;服装出口 1702.8 亿美元,同比增长 24.0%,较 2019 年增长 16.0%。其
中,针织服装及衣着附件出口 864.8 亿美元,同比增长 39.0%;梭织服装及衣着
附件出口701.2亿美元,同比增长 12.6%。
2020年,全国服装出口额比 2019年:
A.增长了10%以上 B.下降了 10%以上
7
更更多多资资料料公公众众号号::考考公公小小镇镇C.增长了不到 10% D.下降了不到 10%
【解析】4.增长/下降+%,求增长率。主体为“服装出口1702.8 亿美元,同
比增长 24.0%,较 2019 年增长 16.0%”,已知 2021 年的同比增速 r 、2021 年比
1
2018年的增长率r ,求2020年比 2019年的增长率 r,代入公式:r=(r -r)
间 2 2 间 1
/(1+r)=(16%-24%)/(1+24%)=-8%/(1+),负数代表下降,排除 A、C 项,
1
数据小于8%,对应 D项。【选D】
【例 5】(2023 深圳)2021 年 1~2 月,全国房地产开发投资 13986 亿元,
同比增长 3873 亿元;房屋施工面积 770629 万平方米,同比增长 11.0%。其中,
住宅 542503 万平方米,增长 11.2%;办公楼 31802 万平方米,增长 7.3%;商业
营业用房76346万平方米,增长 2.5%;其他类型 119978万平方米。房屋新开工
面积 17037 万平方米,增长 64.3%,其中,住宅 12736 万平方米,增长 68.5%。
商品房销售面积 17363 万平方米,同比增长 1.05 倍,比 2019 年 1~2 月增长
23.3%;商品房销售额19151亿元,同比增长1.33倍,比2019年同期增长49.6%。
2020年1~2月,全国商品房销售面积同比增长:
A.-40.0% B.-32.5%
C.40.0% D.17.2%
【解析】5.求 2020 年 1~2 月的同比增长率,主体为“全国商品房销售面
积”,已知“商品房销售面积 17363 万平方米,同比增长 1.05倍,比 2019年1~
2 月增长 23.3%”,“增长 1.05 倍”即 r=1.05,说明增长率为 105%,材料给出 r
、r,求r,代入公式:r=(r -r)/(1+r )=(23%-105%)/(1+105%)=-82%/
间 1 2 2 间 1 1
(2+)≈-40%,对应 A项。【选A】
【注意】概念辨析:增长 1.05倍的意思就是 r=1.05(105%)。
1.有同学认为增长率为 1.05-1=0.05=5%,可以结合例子理解,老邓今年收入
为 10 万,同比增长 0.5 倍,如果按照上述逻辑,增长率=0.5-1=-0.5=-50%,即
收入下降50%,明显不合理。
2.问题是只看到了“1.05倍”,没有看到前面的“增长”。如果表述为“今年
是去年的1.05倍”,则 r=1.05-1=5%;本题的表述为“今年比去年增长 1.05倍”,
8
更更多多资资料料公公众众号号::考考公公小小镇镇则增长率为105%。
2021 年 1~7 月,我国原油产量 11561 万吨,同比增长 2.4%,比 2019 年同
期增长 3.9%。其中,7 月我国原油产量 1686 万吨,增长 2.5%,比 2019 年同期
增长3.1%。
【练习】(2022 江苏)2020年1~7月,我国原油产量的同比增速是:
A.1.46% B.1.90%
C.2.36% D.3.15%
【解析】拓展.课堂正确率为92%。求增长率,主体为“我国原油产量”,已
知“2021 年 1~7 月,我国原油产量 11561 万吨,同比增长 2.4%,比 2019 年同
期增长3.9%”,直接给出 r 、r,求 r,代入公式:r=(r -r)/(1+r )=(3.9%-
间 1 2 2 间 1 1
2.4%)/(1+3.9%)=1.5%/(1+)<1.5%,对应 A项。【选A】
二、年均增长率
例:2015年存款 100万,每年利率都是 10%(复利),18年有多少钱?
年均增长率——比较大小
识别:年均增长最快、年均增速排序
公式:(1+r )n=现期量/基期量(n 为现期和基期的年份差)
年均
技巧:n相同,直接比较“现期/基期”
注:n的确定和年均增长量一样
【注意】年均增长率:每年增速都相同。
1.例:2015年存款 100万,每年利率都是 10%(复利),2018年有多少钱?
(1)假如存100 万,如果单利是5%,则存 1年是5万,2年是 10万,10年
是50万。
9
更更多多资资料料公公众众号号::考考公公小小镇镇(2)如果复利是 10%,相当于“利滚利”,2015 年=100 万,2016 年=100*
(1+10%),2017年=100*(1+10%)*(1+10%)=100*(1+10%)²,2018 年=100*
(1+10%)³,得到年均增长率公式:基期*(1+r )³=现期→(1+r )n=现期
年均 年均
量/基期量。
2.年均增长率——比较大小:
(1)识别:年均增长最快、年均增速排序。
(2)公式:(1+r )n=现期量/基期量(n为现期和基期的年份差)。
年均
(3)技巧:n 相同,直接比较“现期/基期”。
(4)注:n的确定和年均增长量相同。
3.例:小邓 2016 年有 100 万,2024 年有 800 万;小邓 2016 年有 1000 亿,
小马2024年有3000 亿,问谁的年均增长率大。
答:增长率比较,看“现期/基期”,都是 2016~2024 年,年份差 n 相同,
都有“1+”,则不需要考虑,只看“现期/基期”即可。小邓:800 万/100 万=8
倍,小马:3000亿/1000亿=3倍,故小邓年均增长率更大。
【例1】(2023 联考)
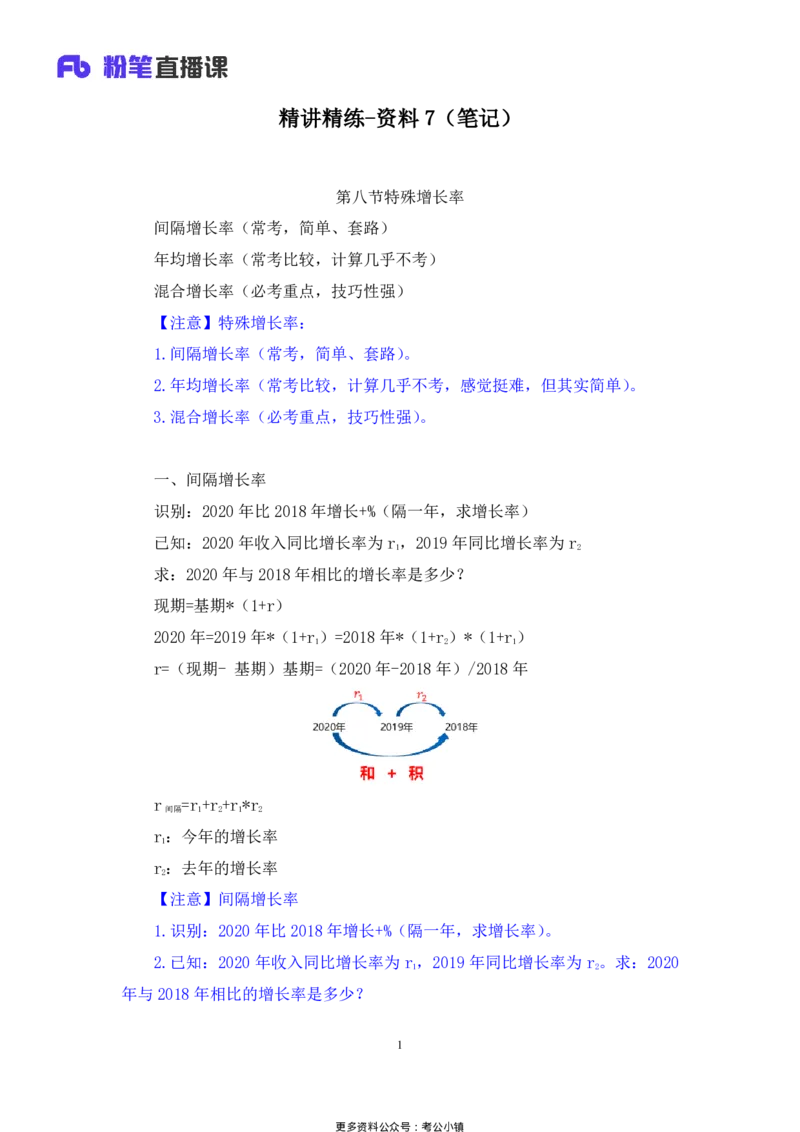
根据资料,判断“2012~2021 年表中的 8 个省份中福建的海水冷却用水量
年平均增速最快”这一说法是否正确。
A.正确 B.错误
【解析】1.比较“年均平均增速”,年均增长率的比较。2012~2021年,年
份差相同,材料给出现期、基期,直接比较“现期/基期=2021 年/2012 年”。福
10
更多资料公众号:考公小镇建:260+/(60+)=4+;其他年份都是1倍多、2倍多,说法正确,对应 A项。【选
A】
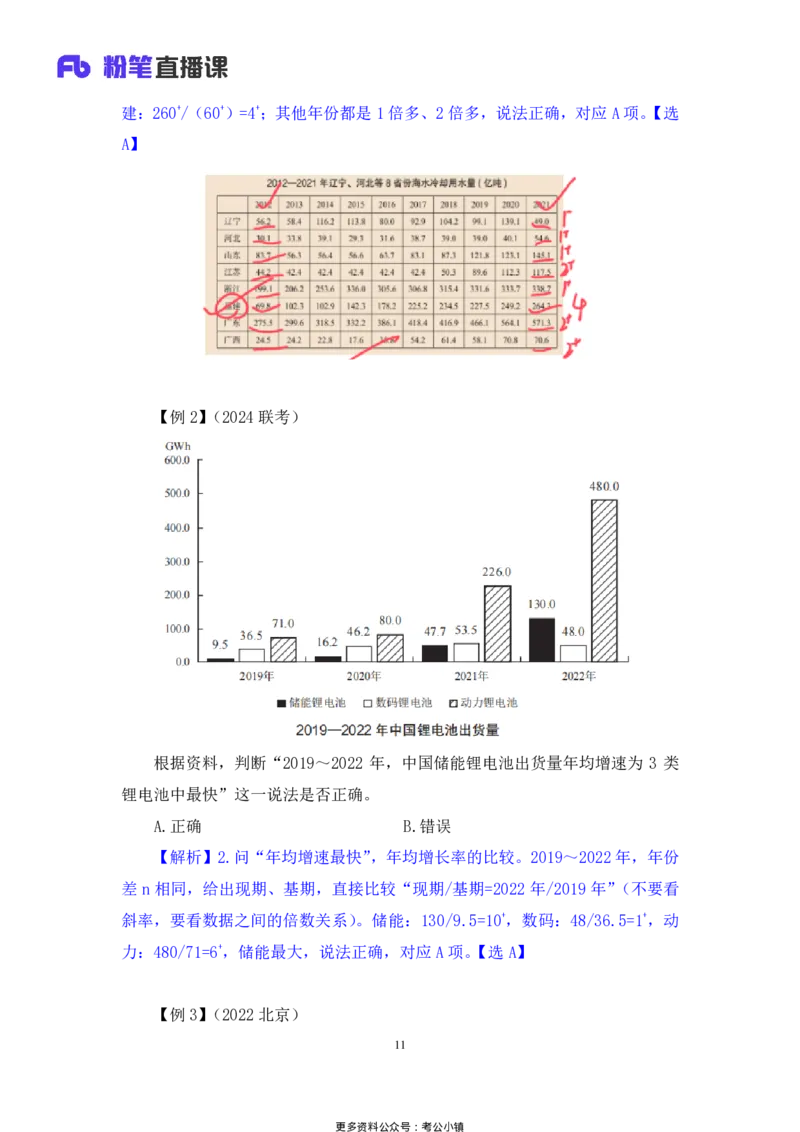
【例2】(2024 联考)
根据资料,判断“2019~2022 年,中国储能锂电池出货量年均增速为 3 类
锂电池中最快”这一说法是否正确。
A.正确 B.错误
【解析】2.问“年均增速最快”,年均增长率的比较。2019~2022 年,年份
差 n 相同,给出现期、基期,直接比较“现期/基期=2022 年/2019 年”(不要看
斜率,要看数据之间的倍数关系)。储能:130/9.5=10+,数码:48/36.5=1+,动
力:480/71=6+,储能最大,说法正确,对应 A项。【选A】
【例3】(2022 北京)
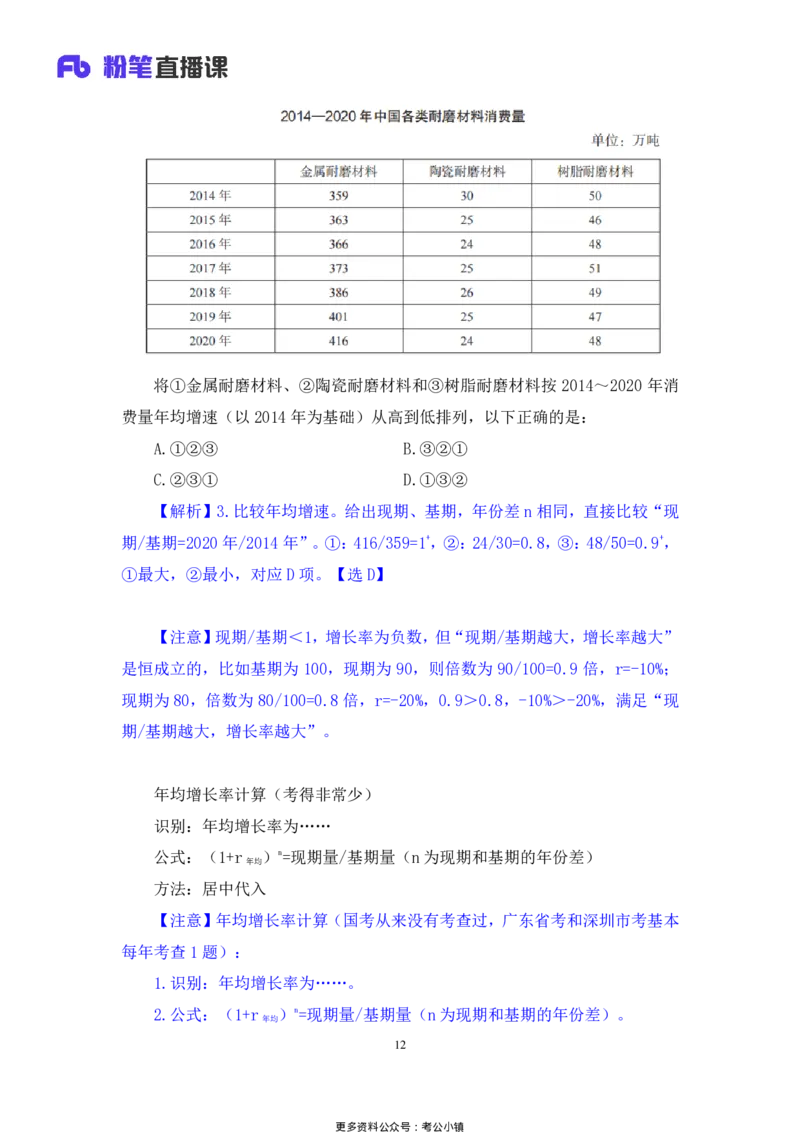
11
更多资料公众号:考公小镇将①金属耐磨材料、②陶瓷耐磨材料和③树脂耐磨材料按 2014~2020 年消
费量年均增速(以 2014年为基础)从高到低排列,以下正确的是:
A.①②③ B.③②①
C.②③① D.①③②
【解析】3.比较年均增速。给出现期、基期,年份差 n相同,直接比较“现
期/基期=2020年/2014 年”。①:416/359=1+,②:24/30=0.8,③:48/50=0.9+,
①最大,②最小,对应 D项。【选D】
【注意】现期/基期<1,增长率为负数,但“现期/基期越大,增长率越大”
是恒成立的,比如基期为 100,现期为 90,则倍数为 90/100=0.9 倍,r=-10%;
现期为80,倍数为 80/100=0.8倍,r=-20%,0.9>0.8,-10%>-20%,满足“现
期/基期越大,增长率越大”。
年均增长率计算(考得非常少)
识别:年均增长率为……
公式:(1+r )n=现期量/基期量(n 为现期和基期的年份差)
年均
方法:居中代入
【注意】年均增长率计算(国考从来没有考查过,广东省考和深圳市考基本
每年考查1题):
1.识别:年均增长率为……。
2.公式:(1+r )n=现期量/基期量(n为现期和基期的年份差)。
年均
12
更多资料公众号:考公小镇3.方法:居中代入。
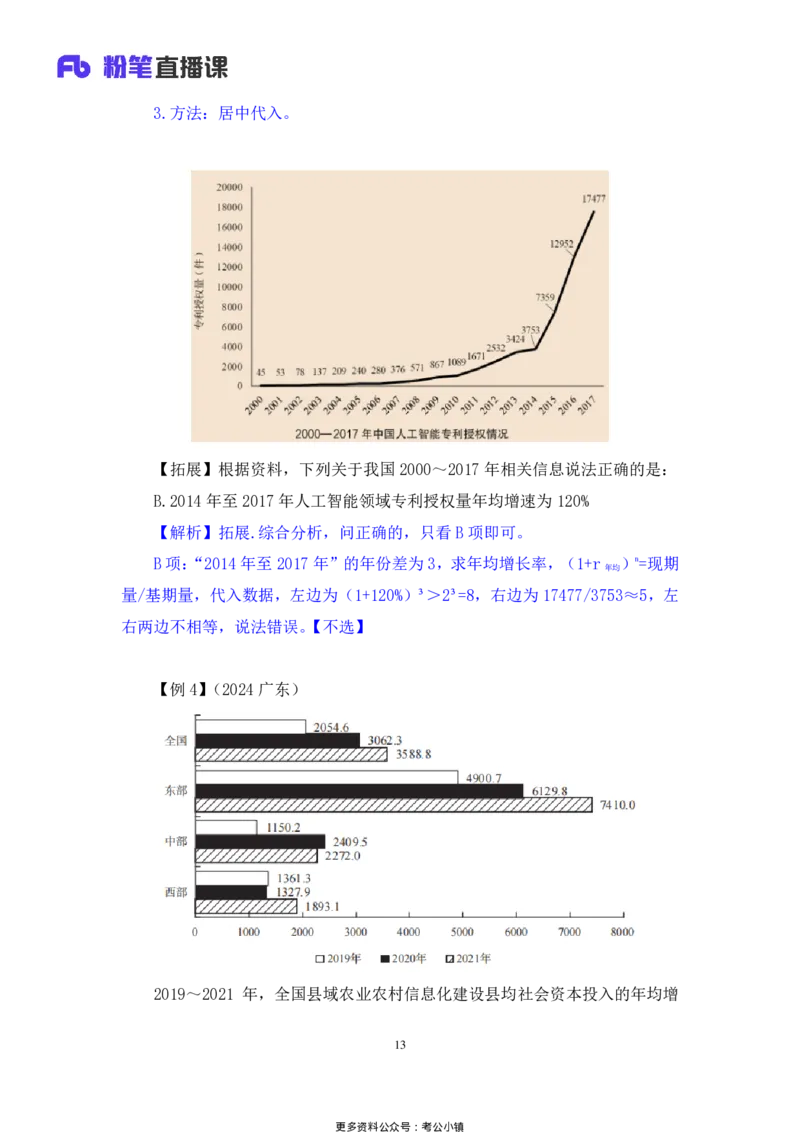
【拓展】根据资料,下列关于我国 2000~2017年相关信息说法正确的是:
B.2014年至2017 年人工智能领域专利授权量年均增速为 120%
【解析】拓展.综合分析,问正确的,只看 B项即可。
B项:“2014年至 2017年”的年份差为 3,求年均增长率,(1+r )n=现期
年均
量/基期量,代入数据,左边为(1+120%)³>2³=8,右边为 17477/3753≈5,左
右两边不相等,说法错误。【不选】
【例4】(2024 广东)
2019~2021 年,全国县域农业农村信息化建设县均社会资本投入的年均增
13
更多资料公众号:考公小镇长率约为:
A.10% B.21%
C.32% D.43%
【解析】4.求年均增长率,公式:(1+r )n=现期量/基期量。问题时间为
年均
“2019~2021 年”,现期为 2021 年,基期为 2019 年,年份差为 2。右边=现期/
基期=3588/2050,截两位看作 3588/21,首位商 1,次位商7,结果为 1.7+;居住
代入30%,左边=(1+30%)²=1.69,代入的 30%略小一点,实际年均增长率比 30%
略大一点点,对应 C项。【选C】
【注意】D项:1.4²=1.96>1.7,排除 D项。
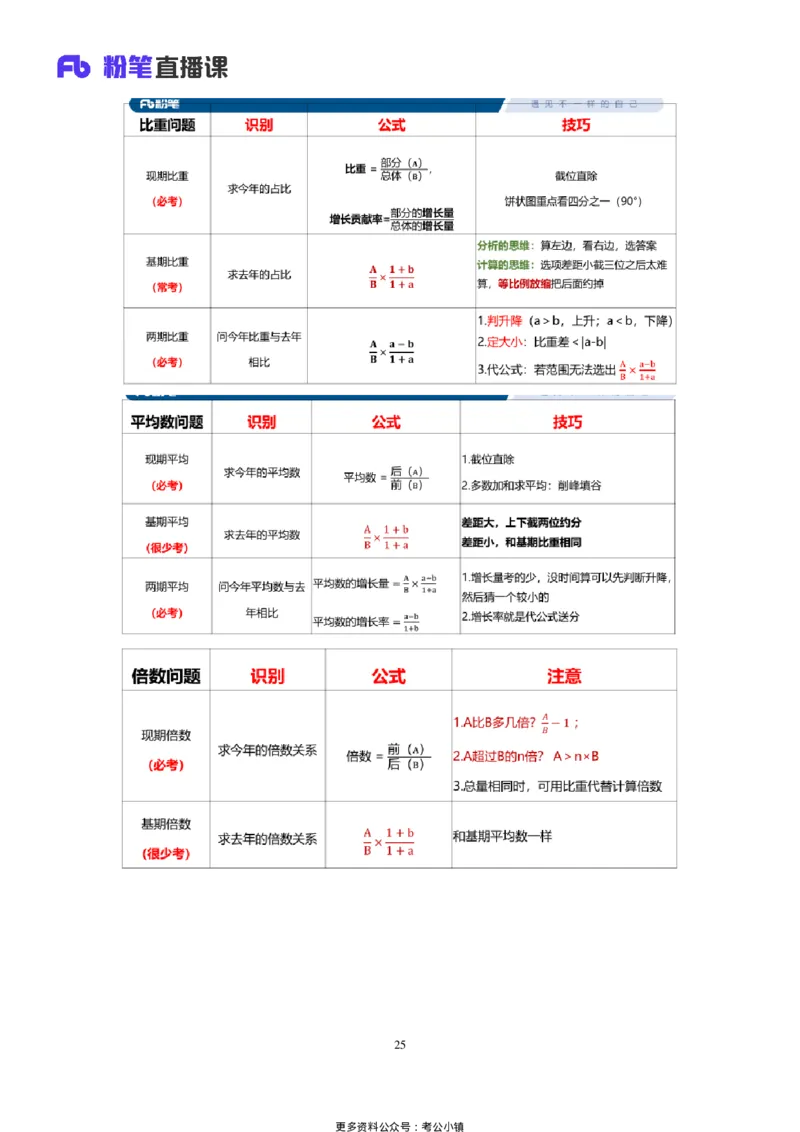
三、混合增长率
三、混合增长率
题型识别:
①求增长率,无法直接计算
②主体之间有和差关系
例:已知前三季度增长率,四季度增长率,求全年增长率。
例如:
①固定搭配:进口+出口=进出口、城镇+农村=全国、邮政+电信=邮电
②时间累计型:1至11月+12月=全年、一季度+二季度=上半年
③逻辑型:A+非A=全部(实物+非实物=所有商品)
判断口诀:
(1)混合后总体居中(最小 r<总体 r<最大r)
补例 1:2019 年进口增长了 10%,出口增长了 20%,则进出口可能增长了
多少?
A.8% B.9%
C.14% D.21%
补例 2:2019 年进出口增长了 10%,出口增长了 20%,则进口可能增长了
多少?
14
更多资料公众号:考公小镇A.8% B.12%
C.14% D.21%
【注意】混合增长率:
1.题型识别:
(1)求增长率,没有数据,无法直接计算。
(2)求的主体和材料之间有和差关系。
(3)例:已知前三季度增长率、四季度增长率,求全年增长率?材料中
没有全年,前三季度+第四季度=全年(是量有加和关系,不是率)。
2.和差关系:
(1)固定搭配:进口+出口=进出口、邮政+电信=邮电。出现邮电方面和
进出口方面的材料可以想到考查混合增长率。
(2)时间累计型:1至11月+12月=全年、一季度+二季度=上半年。
(3)逻辑型:A+非A=全部。比如男生+女生=总人数;实物+非实物=全部。
3.判断口诀:混合后总体居中(最小 r<总体r<最大r)。
(1)如男生人均身高 190cm、女生人均身高 170cm,男生、女生混合后,
身高不可能是360cm,人均身高在 170~190cm之间,增长率混合同理,混合之
后总体居中,最小 r<总体r<最大r。
(2)补例1:2019年进口增长了10%,出口增长了 20%,则进出口可能增
长了多少?
A.8% B.9%
C.14% D.21%
答:进口+出口=进出口,混合后总体居中,则 10%<r <20%,只有 C项
进出口
符合。
(3)补例2:2019年进出口增长了10%,出口增长了 20%,则进口可能增
长了多少?
A.8% B.12%
C.14% D.21%
答:进口+出口=进出口,r 居中,r <r (10%)<r (20%),
进出口 进口 进出口 出口
只有A项符合。
15
更多资料公众号:考公小镇【例 1】(2023 山东)2021 年,中国跨境电商交易规模达 14.2 万亿元,占
我国货物进出口总额的比例为 36.3%。其中出口跨境电商交易规模 11 万亿元,
同比增速 13.4%;进口跨境电商交易规模 3.2 万亿元,同比增速 14.3%。2017—
2022年第一季度,中国跨境电商领域共发生 262次投资,投资总金额 654.91亿
元。
2021年,我国跨境电商交易规模同比增长:
A.12.8% B.13.4%
C.13.6% D.14.3%
【解析】1.求我国跨境电商交易规模的增长率,本题模仿国考,国考说的是
“跨境进出口”,本题没写全,“跨境”即和境外做买卖,就是进出口的情况,材
料中分为进口和出口,进出口=进口+出口,混合后总体居中,则r 介于13.4%~
进出口
14.3%之间,只有C 项符合。【选C】
【注意】选项设计:B项为出口、D项为进口,C项刚好居中。
【例2】(2022江苏)2020年江苏省全省网上零售额10602亿元,增长10.0%。
其中,实物商品网上零售额增长 13.9%,增速比上年快 5.2个百分点,占社会消
费品零售总额37086 亿元的比重为24.9%,提高 2.7个百分点。
根据资料,判断“2020年江苏非实物商品网上零售额增速高于 13.9%”这一
说法是否正确。
A.正确 B.错误
【解析】2.出现非实物,求增速,非实物+实物=总体,考虑混合增长率。混
合后总体居中,r =10%,r =13.9%,则r <10%<13.9%,说法错误,对应
全省 实物 非实物
B项。【选B】
【注意】多年没有考查过 3者混合,之前江苏考查过,可以先两者混合,得
到范围后再和另一个混合,方法是一样的。
16
更多资料公众号:考公小镇【例3】(2025 四川)2022 年上半年,我国软件与信息技术服务业总收入同
比增长 10.9%,增速较 1—5 月份提高 0.3 个百分点。软件与信息技术服务业收
入中,软件产品收入、信息技术服务收入、信息安全收入、嵌入式系统软件收入
同比分别增长10.2%、12%、11.4%和5%。信息技术服务收入中,云计算、大数据
服务收入 4790 亿元,同比增长 9.3%;集成电路设计收入 1279 亿元,同比增长
15.2%。
根据资料,判断“2022 年 6 月,我国软件与信息技术服务业总收入增速超
过10%”这一说法是否正确。
A.正确 B.错误
【解析】3.求 6 月的增速,给出 1~6 月和 1~5 月,上半年=6 月+1~5 月,
考虑混合增长率,混合之后整体居中,上半年增速 10.9%,1~5 月增速=10.9%-
0.3%=10.6%,1~5 月增速 10.6%<上半年增速 10.9%<6 月增速,正确,对应 A
项。【选A】
【例4】(2023 广东)2022 年,全国居民人均可支配收入 36883 元,比上年
增长(以下如无特别说明,均为同比名义增长)5.0%。分城乡看,城镇居民人均
可支配收入49283元,增长3.9%;农村居民人均可支配收入20133元,增长6.3%。
2022 年,全国居民人均消费支出 24538 元,比上年增长 1.8%。分城乡看,
城镇居民人均消费支出 30391元,增长 0.3%;农村居民人均消费支出 16632元,
增长4.5%。
2022年,全国居民人均收支盈余比上一年:(注:收支盈余=收入-消费支出)
A.增加了约5% B.减少了约 5%
C.增加了约12% D.减少了约 12%
【解析】4.比如一个月收入10000,支出8000还房贷,盈余10000-8000=2000,
收支盈余=收入-消费支出→收入=消费支出+收支盈余,存在加和关系,求增长率,
为混合增长率问题。混合后总体居中,r (1.8%)<r (5%)<r ,仅 C项
支出 收入 盈余
符合。【选C】
【注意】偏向量大的,支出的量为 24538,盈余的量为36883-24538≈12000,
17
更多资料公众号:考公小镇支出量大,总体的增长率偏向支出增长率 1.8%,即左边距离小于右边距离,5%-
1.8%=3.2%,则右边距离大于 3.2%,所求>5%+3.2%=8.2%,不能选择 5%。
②偏向基数较大的(材料无基期,做题时用现期近似代替基期)
例:100gA溶液浓度 5%,100gB溶液浓度 10%,混合之后浓度?
A.6% B.7.5%
C.9%
例:100gA溶液浓度 5%,400gB溶液浓度 10%,混合之后浓度?
A.6% B.7.5%
C.9%
例:出口400万同比增速 5%,进口 100 万同比增速10%,混合之后增速约?
A.6% B.7.5%
C.9%
【注意】偏向基数较大的:
1.例:男生人均身高 190cm、女生人均身高 170cm,如果男生人数=女生人数,
全班人均身高=180cm。如果男生人数>女生人数,则全班人均身高在 180~190cm
之间;如果男生人数<女生人数,则全班人均身高在 170~180cm 之间。线段法
可以看成一个天平或者拔河,如果左右两边势均力敌,则会在中间维持平衡,如
果右边量多,则向右边倾斜,靠近右边,如果左边量多,则向左边倾斜。
2.增长率=增长量/基期,增长率的量是基期量,但是题目一般都给现期量,
看偏向用现期近似代替基期,偏向现期量大的。
3.例1:100gA 溶液浓度5%,100gB溶液浓度 10%,混合之后浓度?
A.6% B.7.5%
C.9%
答:等量混合,混合后浓度正好在中点,(5%+10%)/2=7.5%,选择 B项。
4.例2:100gA 溶液浓度5%,400gB溶液浓度 10%,混合之后浓度?
A.6% B.7.5%
C.9%
答:B溶液更多,偏向10%,在7.5%~10%之间,选择C项。
18
更多资料公众号:考公小镇4.例:出口 400 万同比增速 5%,进口 100 万同比增速 10%,混合之后增速
约?
A.6% B.7.5%
C.9%
答:出口量更多,应该更靠近 5%,则总体在5%~7.5%之间,选择 A项。
【例5】(2021新疆兵团)2018年H市完成邮电业务总量 108.2亿元。其中,
邮政业务总量40.8 亿元,同比增长26.5%;电信业务总量 67.4亿元,同比增长
56.7%。
年末移动电话用户达到 341 万户,其中,3G 移动电话用户达到 25.7 万户,
4G移动电话用户达到 241.4万户。全市互联网接入用户 89.9万户,其中,新增
互联网用户23.8万户。
2018年H市邮电业务总量同比增速在下列哪一个范围内?
A.23%~41% B.41%~57%
C.57%~71% D.高于 71%
【解析】5.邮电业务后面有“其中”,邮电业务分为邮政业务和电信业务两
部分,考虑混合增长率,混合后居中,邮电业务增速介于 26.5%~56.7%之间,排
除C、D项。邮政业务:r=26.5%、量≈40亿元,电信业务:r=56.7%、量≈67亿
元,电信业务的量大,应该偏向电信业务,结合选项,选择B项。
不结合选项,自己看偏向的话,需要找中点,中点=(26.5%+56.7%)/2=41.6%,
r 介于41.6%~56.7%之间,选择B项。【选 B】
邮电业务
【注意】r 介于41.6%~56.7%之间,选项范围要大于标准答案的范围才
邮电业务
能够选,假设月收入是 5万,选项分别是A.1~3万,B.4~6万,选择 B项;标
准结果是r 介于 41.6%~56.7%之间,B 项范围全部包含标准结果,在标准结
邮电业务
果中取任意值,都包含在 B项中,故可以选择 B项。
【例 6】(2025 四川)2023 年上半年,全国新注册登记机动车 1688 万辆,
19
更多资料公众号:考公小镇同比增长1.9%。新注册登记汽车 1175万辆,同比增长 5.8%。其中,新注册登记
载客汽车1034万辆,同比增长 5.6%;新注册登记载货汽车 133万辆,同比增长
8.1%。新注册登记新能源汽车 313万辆,同比增长 41.6%。
2023年上半年,全国新注册登记非汽车类机动车数量比上年同期:
A.增长了不到 2% B.增长了 2%以上
C.减少了不到 2% D.减少了 2%以上
【解析】6.问题时间是 2023 年上半年,出现“非”,机动车=汽车+非汽车,
求增长率,混合增长率,混合之后整体居中,非汽车增速<机动车增速 1.9%<汽
车增速 5.8%,只能排除 B 项;再看偏向,偏向量大的,汽车量为 1175,机动车
量为 1688,非汽车量为 1688-1755≈500,偏向汽车,左边距离小,右边距离为
5.8%-1.9%=3.9%,左边距离<3.9%,所求<1.9%-3.9%=-2%,临界值是-2%,距离
比3.9个百分点更大,故减少了2%以上,对应 D项。【选D】
知识点拓展——线段法(用于混合增长率的精确计算)
解题逻辑:
混合增长率的题目先用口诀“混合之后总体居中,偏向量大的”来解决(90%
以上);
如果无法锁定唯一答案才需要用线段法计算
线段法的运用口诀:
1.部分在两边,总体在中间;
2.距离和量成反比。
例:溶液A克,浓度 a%;溶液 B克,浓度 b%。混合后的溶液浓度为 x%(a<
x<b)
20
更多资料公众号:考公小镇3分钟证明原理,感兴趣就听,不感兴趣就记操作
练习 1:全年消费 4000 元,同比增长 5%,上半年消费 1000 元,同比增长
2%,下半年消费3000 元,问下半年消费同比增长率为多少?
练习:上半年收入 5 万元,同比增长 12%,1~5 月收入 4 万元,同比增长
10%,问6月收入同比增速约为多少?
【注意】线段法:
1.例:溶液A克,浓度 a%;溶液 B克,浓度 b%。混合后的溶液浓度为 x%(a
<x<b)。
(1)比如盐水中,盐是溶质,水是溶剂,盐水是溶液,溶液*浓度=溶质,A
溶质+B 溶质=总溶质,则 A*a%+B*b%=(A+B)*x%→Aa+B*b=A*x+B*x→Bb-Bx=Ax-
Aa→B(b-x)=A(x-a)→(b-x)/(x-a)=A/B。
(2)用线段的形式体现,下面是→,A 和B,上面有三个点,三个点之间的
距离为x-a和b-x,距离和量成反比,A:B=(b-x)/(x-a)。
2.练习:
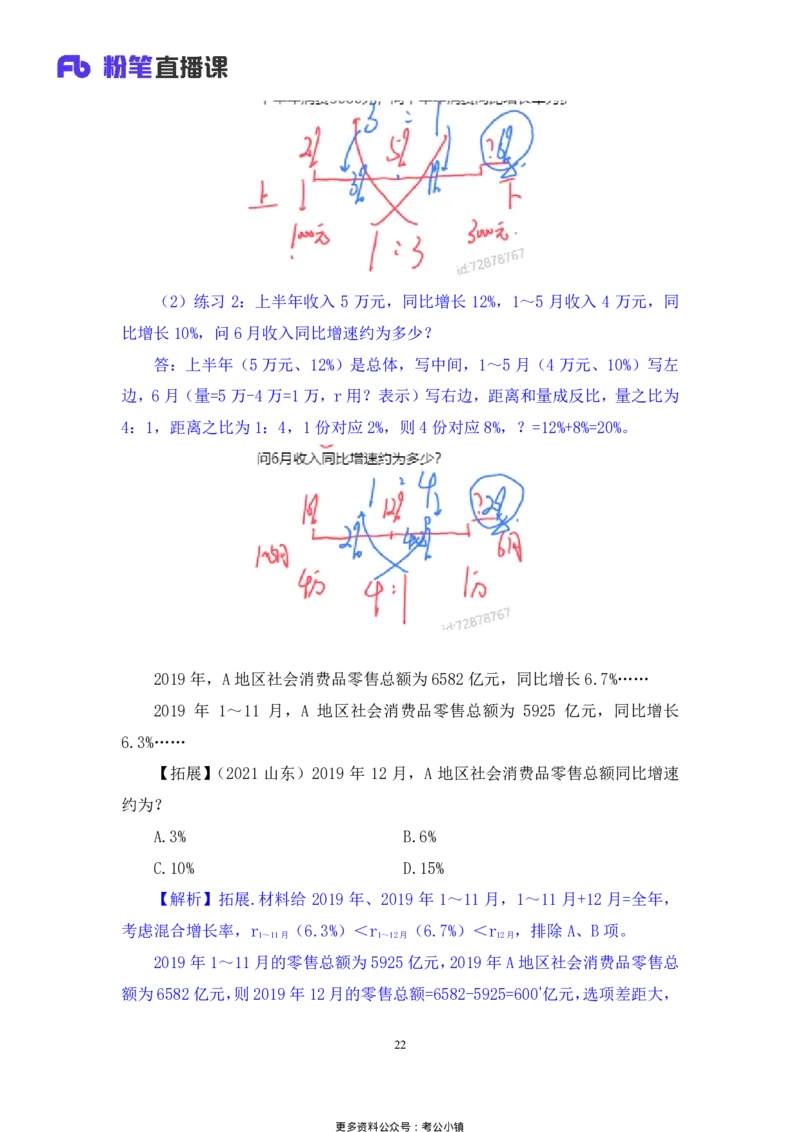
(1)练习 1:全年消费 4000 元,同比增长 5%,上半年消费 1000 元,同比
增长2%,下半年消费 3000元,问下半年消费同比增长率为多少?
答:上半年(1000 元、2%)写左边,下半年(3000 元、?)写右边,全年
(5%)写中间,量之比=1000:3000=1:3,距离和量成反比,则距离之比=3:1,
2%到5%的距离是3%,3%对应3份,则1份对应 1%,r =5%+1%=6%。
下半年
21
更多资料公众号:考公小镇(2)练习 2:上半年收入 5 万元,同比增长 12%,1~5 月收入 4 万元,同
比增长10%,问6月收入同比增速约为多少?
答:上半年(5 万元、12%)是总体,写中间,1~5月(4万元、10%)写左
边,6月(量=5万-4万=1万,r 用?表示)写右边,距离和量成反比,量之比为
4:1,距离之比为 1:4,1份对应2%,则4 份对应8%,?=12%+8%=20%。
2019年,A地区社会消费品零售总额为 6582亿元,同比增长6.7%……
2019 年 1~11 月,A 地区社会消费品零售总额为 5925 亿元,同比增长
6.3%……
【拓展】(2021 山东)2019 年 12 月,A 地区社会消费品零售总额同比增速
约为?
A.3% B.6%
C.10% D.15%
【解析】拓展.材料给 2019 年、2019 年 1~11 月,1~11 月+12 月=全年,
考虑混合增长率,r (6.3%)<r (6.7%)<r ,排除A、B 项。
1~11月 1~12月 12月
2019年1~11 月的零售总额为5925亿元,2019年A地区社会消费品零售总
额为6582亿元,则2019年12月的零售总额=6582-5925=600+亿元,选项差距大,
22
更多资料公众号:考公小镇不用很精确,量之比近似为 5900:600+≈10:1,距离和量成反比,则距离之比
≈1:10,左边 6.7%-6.3%=0.4%对应1份,10 份对应4%,r ≈6.7%+4%=10.7%,
12月
对应C项。【选C】
23
更多资料公众号:考公小镇24
更多资料公众号:考公小镇25
更多资料公众号:考公小镇复习建议(最后再唠叨几句)
1、课程至少再看一遍,重点看不懂的地方,查缺补漏,不留死角。
2、把每天上课的知识点、思维导图,手写整理成笔记。
要求:根据我给的模板内容调整成自己的内容
3、找数与速算的练习:微信小程序“粉笔快练”
4、基础扎实后,每天做 3~4篇资料分析。
注意:前期以正确率为主,准确率达到 80%左右后掐时间
5、请你坚持,资料分析一定会提高
26
更多资料公众号:考公小镇【注意】复习建议(最后再唠叨几句):
1.课程至少再看一遍,重点看不懂的地方,查缺补漏,不留死角。
2.把每天上课的知识点、思维导图,手写整理成笔记。要求根据老师给的模
板内容调整成自己的内容。
3.找数与速算的练习:微信小程序“粉笔快练”,最重要的如上图,是老师
27
更多资料公众号:考公小镇圈出来的首位计算和百分数与分数。
4.基础扎实后,每天做 3~4 篇资料分析。注意前期以正确率为主,准确率
达到80%左右后掐时间。
5.请你坚持,资料分析一定会提高。
6.系统班使用说明书:
(1)精讲精练阶段:对应《笔试系统讲义》。
(2)刷题巩固阶段:每个科目会给大家讲解三套真题,配套讲义是《极致
试题》。
(3)拔高突破阶段:对应讲义是《拔高突破讲义》。
(4)考前冲刺阶段:讲义是课前老师结合最新真题来给大家现做的。
(5)除了核心课程还有补充课程,补充课程一般会有 300+节,公安专业理
论微课、常识及政治理论热点课、常识补充考点课是提前添加的录播课;阶段梳
理课是跟随精讲精练科目的进行而添加的。一些稀奇古怪考法还会陆续添加补充
课,大家可以按需听。
(6)图书大礼包:《行测的思维》和《申论的规矩》可以当成工具书、百科
全书来用,《行测考点一本通》和《申论技巧与热点解读》是知识点小册子,《常
识通关三百问》和《公安必备考点》也是包含在大礼包中,大家可以结合使用。
【答案汇总】
间隔增长率1-5:DBBDA
年均增长率1-4:AADC
混合增长率1-5:CBACB;6:D
28
更多资料公众号:考公小镇遇见不一样的自己
Be your better self
29
更多资料公众号:考公小镇