文档内容
专题 14 指数、对数、幂函数、
函数图象、函数零点及函数模型的应用
考点 十年考情(2015-2024) 命题趋势
考点1 指数函数 2023·全国乙卷、2023·全国新Ⅰ卷、2022·北京卷
及其应用 2017·全国、2016·北京、2015·江苏、
(10年5考) 2015·山东卷、2015·福建卷
2024·全国甲卷、2023·北京卷、2022·天津卷
考点2 对数运算 2022·浙江卷、2022·全国乙卷、2021·天津卷
及指对互化 2020·全国卷、2018·全国卷、2016·浙江卷
(10年8考) 2015·浙江卷、2015·浙江卷、2015·四川卷
2015·上海卷、2015·上海卷、2015·安徽卷
1. 掌握指数对数幂函数的图象
考点3 对数函数 2024·北京卷、2024·全国新Ⅰ卷、2020·全国新Ⅱ
与性质,会指数对数的相关运
及其应用 卷2020·全国卷、2020·北京卷、2015·重庆卷
算,会指对幂函数值的大小比
(10年3考) 2015·四川卷、2015·湖北卷、2015·北京卷
较,都是高考命题的方向
考点4 幂函数
2024·天津卷、2023·北京卷、2020·江苏卷 2. 掌握函数图象的判断方法
(10年3考)
3. 掌握函数零点的定义,会用
2024·天津卷、2023·全国甲卷、2023·天津卷
零点存在定理判断零点所在区
2022·天津卷、2022·全国甲卷、2022·全国新Ⅰ卷
间,会求解零点相关问题,也
考点5 指对幂函 2021·天津卷、2021·全国新Ⅱ卷、2020·天津卷
是高考命题的高频考点
数值大小比较 2020·全国卷、2020·全国卷、2020·全国卷
4. 掌握函数模型及其应用
(10年10考) 2019·天津卷、2019·天津卷、2018·天津卷
2017·全国卷、2016·全国卷、2016·全国卷
2015·重庆卷、2015·陕西卷、2015·山东卷
2024·全国甲卷、2023·天津卷、2022·全国乙卷
2022·全国甲卷、2022·天津卷、2021·浙江卷
考点6 函数图象
2020·天津卷、2020·浙江卷、2019·浙江卷
(10年8考)
2018·全国卷、2018·浙江卷、2018·全国卷
2017·全国卷、2017·全国卷、2015·安徽卷2015·浙江卷
2024·全国新Ⅰ卷、2024·全国新Ⅱ卷、2024·全国
新Ⅱ卷、2024·全国甲卷、2024·天津卷、2023·天
津卷、2023·全国新Ⅰ卷、2022·天津卷、2022·北
京卷
2021·北京卷、2021·天津卷、2020·天津卷
考点7 函数零点 2019·全国卷、2019·浙江卷、2019·江苏卷
及其应用 2018·全国卷、2018·浙江卷、2018·天津卷
(10年10考) 2018·全国卷、2017·山东卷、2017·江苏卷
2016·江苏卷、2016·天津卷、2016·天津卷
2016·天津卷、2016·天津卷、2015·天津卷
2015·天津卷、2015·安徽卷、2015·江苏卷
2015·湖北卷、2015·湖北卷、2015·安徽卷
2015·湖南卷、2015·湖南卷
考点8 函数模型 2024·北京卷、2022·北京卷、2021·全国甲卷
(10年5考) 2019·北京卷、2017·北京卷
考点01 指数函数及其应用
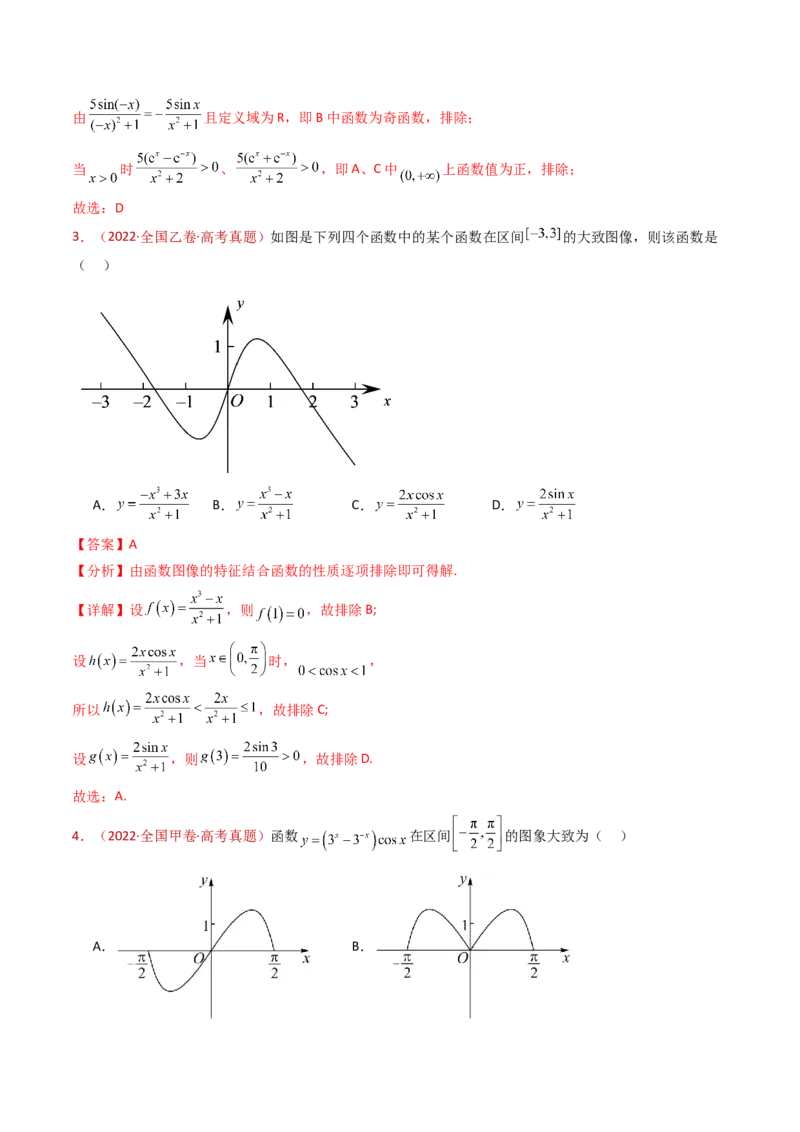
1.(2023·全国乙卷·高考真题)已知 是偶函数,则 ( )
A. B. C.1 D.2
【答案】D
【分析】根据偶函数的定义运算求解.
【详解】因为 为偶函数,则 ,
又因为 不恒为0,可得 ,即 ,
则 ,即 ,解得 .
故选:D.
2.(2023·全国新Ⅰ卷·高考真题)设函数 在区间 上单调递减,则 的取值范围是( )
A. B.
C. D.
【答案】D【分析】利用指数型复合函数单调性,判断列式计算作答.
【详解】函数 在R上单调递增,而函数 在区间 上单调递减,
则有函数 在区间 上单调递减,因此 ,解得 ,
所以 的取值范围是 .
故选:D
3.(2022·北京·高考真题)已知函数 ,则对任意实数x,有( )
A. B.
C. D.
【答案】C
【分析】直接代入计算,注意通分不要计算错误.
【详解】 ,故A错误,C正确;
,不是常数,故BD错误;
故选:C.
4.(2017·全国·高考真题)设函数 则满足 的x的取值范围是
.
【答案】
【详解】由题意得: 当 时, 恒成立,即 ;当 时,
恒成立,即 ;当 时, ,即 .综上,x的取值范围
是 .
5.(2016·北京·高考真题)下列函数中,在区间 上为减函数的是
A. B. C. D.
【答案】D
【详解】试题分析: 在区间 上为增函数; 在区间 上先增后减; 在
区间 上为增函数; 在区间 上为减函数,选D.考点:函数增减性
6.(2015·江苏·高考真题)不等式 的解集为 .
【答案】
【详解】试题分析:本题是一个指数型函数式的大小比较,这种题目需要先把底数化为相同的形式,即底
数化为2,根据函数是一个递增函数,写出指数之间的关系得到未知数的范围.
,
是一个递增函数;
故答案为 .
考点:指数函数的单调性和特殊性
7.(2015·山东·高考真题)已知函数 的定义域和值域都是 ,则
.
【答案】
【详解】若 ,则 在 上为增函数,所以 ,此方程组无解;
若 ,则 在 上为减函数,所以 ,解得 ,所以 .
考点:指数函数的性质.
8.(2015·福建·高考真题)若函数 满足 ,且 在 单调递增,
则实数 的最小值等于 .
【答案】
【详解】试题分析:根据 可知函数 的图像关于直线 对称,可知 ,从而可
以确定函数 在 上是增函数,从而有 ,所以 ,故 的最小值等于 .
考点:函数图像的对称性,函数的单调性.
【方法点睛】该题根据题中的条件确定好函数本身的单调区间,根据函数在函数增区间的所有子区间上是
增函数,从而求得参数的取值范围,关键是根据条件 ,得出函数图像的对称性,确定
出函数图像的对称轴,从而得到函数的增区间,从而根据集合间的包含关系,从而确定出参数的取值范围.
考点02 对数运算及指对互化
1.(2024·全国甲卷·高考真题)已知 且 ,则 .【答案】64
【分析】将 利用换底公式转化成 来表示即可求解.
【详解】由题 ,整理得 ,
或 ,又 ,
所以 ,故
故答案为:64.
2.(2023·北京·高考真题)已知函数 ,则 .
【答案】1
【分析】根据给定条件,把 代入,利用指数、对数运算计算作答.
【详解】函数 ,所以 .
故答案为:1
3.(2022·天津·高考真题)化简 的值为( )
A.1 B.2 C.4 D.6
【答案】B
【分析】根据对数的性质可求代数式的值.
【详解】原式
,
故选:B
4.(2022·浙江·高考真题)已知 ,则 ( )
A.25 B.5 C. D.
【答案】C
【分析】根据指数式与对数式的互化,幂的运算性质以及对数的运算性质即可解出.
【详解】因为 , ,即 ,所以 .
故选:C.
5.(2022·全国乙卷·高考真题)若 是奇函数,则 , .【答案】 ; .
【分析】根据奇函数的定义即可求出.
【详解】[方法一]:奇函数定义域的对称性
若 ,则 的定义域为 ,不关于原点对称
若奇函数的 有意义,则 且
且 ,
函数 为奇函数,定义域关于原点对称,
,解得 ,
由 得, ,
,
故答案为: ; .
[方法二]:函数的奇偶性求参
函数 为奇函数
[方法三]:
因为函数 为奇函数,所以其定义域关于原点对称.
由 可得, ,所以 ,解得: ,即函数的定义域为,再由 可得, .即 ,在定义域
内满足 ,符合题意.
故答案为: ; .
6.(2021·天津·高考真题)若 ,则 ( )
A. B. C.1 D.
【答案】C
【分析】由已知表示出 ,再由换底公式可求.
【详解】 , ,
.
故选:C.
7.(2020·全国·高考真题)设 ,则 ( )
A. B. C. D.
【答案】B
【分析】根据已知等式,利用指数对数运算性质即可得解
【详解】由 可得 ,所以 ,
所以有 ,
故选:B.
【点睛】本题考查的是有关指对式的运算的问题,涉及到的知识点有对数的运算法则,指数的运算法则,
属于基础题目.
8.(2018·全国·高考真题)已知函数 ,若 ,则 .
【答案】-7
【详解】分析:首先利用题的条件 ,将其代入解析式,得到 ,从而得到
,从而求得 ,得到答案.
详解:根据题意有 ,可得 ,所以 ,故答案是 .
点睛:该题考查的是有关已知某个自变量对应函数值的大小,来确定有关参数值的问题,在求解的过程中,
需要将自变量代入函数解析式,求解即可得结果,属于基础题目.
9.(2016·浙江·高考真题)已知a>b>1.若logb+log a= ,ab=ba,则a= ,b= .
a b【答案】
【详解】试题分析:设 ,因为 ,
因此
指数运算,对数运算.
在解方程 时,要注意 ,若没注意到 ,方程 的根有两个,
由于增根导致错误
10.(2015·浙江·高考真题)计算: , .
【答案】
【详解】 ; .
考点:对数运算
11.(2015·浙江·高考真题)若 ,则 .
【答案】
【详解】∵ ,∴ ,∴ .
考点:对数的计算
12.(2015·四川·高考真题)lg0.01+log 16= .
2
【答案】2
【详解】lg0.01+log 16=-2+4=2
2
考点:本题考查对数的概念、对数运算的基础知识,考查基本运算能力.
13.(2015·上海·高考真题)方程 的解为 .
【答案】2
【详解】依题意 ,所以 ,
令 ,所以 ,解得 或 ,
当 时, ,所以 ,而 ,所以 不合题意,舍去;
当 时, ,所以 , , ,所以 满足条件,
所以 是原方程的解.
考点:对数方程.
14.(2015·上海·高考真题)方程 的解为 .
【答案】【详解】设 ,则
考点:解指对数不等式
15.(2015·安徽·高考真题) .
【答案】-1
【详解】原式=
考点:本题主要考查对数运算公式和指数幂运算公式.
考点03 对数函数及其应用
1.(2024·北京·高考真题)已知 , 是函数 的图象上两个不同的点,则( )
A. B.
C. D.
【答案】B
【分析】根据指数函数和对数函数的单调性结合基本不等式分析判断AB;举例判断CD即可.
【详解】由题意不妨设 ,因为函数 是增函数,所以 ,即 ,
对于选项AB:可得 ,即 ,
根据函数 是增函数,所以 ,故B正确,A错误;
对于选项D:例如 ,则 ,
可得 ,即 ,故D错误;
对于选项C:例如 ,则 ,
可得 ,即 ,故C错误,
故选:B.
2.(2024·全国新Ⅰ卷·高考真题)已知函数 在R上单调递增,则a的取值范围是
( )
A. B. C. D.【答案】B
【分析】根据二次函数的性质和分界点的大小关系即可得到不等式组,解出即可.
【详解】因为 在 上单调递增,且 时, 单调递增,
则需满足 ,解得 ,
即a的范围是 .
故选:B.
3.(2020·全国新Ⅱ卷·高考真题)已知函数 在 上单调递增,则 的取值范围是
( )
A. B. C. D.
【答案】D
【分析】首先求出 的定义域,然后求出 的单调递增区间即可.
【详解】由 得 或
所以 的定义域为
因为 在 上单调递增
所以 在 上单调递增
所以
故选:D
【点睛】在求函数的单调区间时一定要先求函数的定义域.
4.(2020·全国·高考真题)设函数 ,则f(x)( )
A.是偶函数,且在 单调递增 B.是奇函数,且在 单调递减
C.是偶函数,且在 单调递增 D.是奇函数,且在 单调递减
【答案】D
【分析】根据奇偶性的定义可判断出 为奇函数,排除AC;当 时,利用函数单调性的性质
可判断出 单调递增,排除B;当 时,利用复合函数单调性可判断出 单调递减,从而
得到结果.
【详解】由 得 定义域为 ,关于坐标原点对称,
又 ,为定义域上的奇函数,可排除AC;
当 时, ,
在 上单调递增, 在 上单调递减,
在 上单调递增,排除B;
当 时, ,
在 上单调递减, 在定义域内单调递增,
根据复合函数单调性可知: 在 上单调递减,D正确.
故选:D.
【点睛】本题考查函数奇偶性和单调性的判断;判断奇偶性的方法是在定义域关于原点对称的前提下,根
据 与 的关系得到结论;判断单调性的关键是能够根据自变量的范围化简函数,根据单调性的
性质和复合函数“同增异减”性得到结论.
5.(2020·北京·高考真题)函数 的定义域是 .
【答案】
【分析】根据分母不为零、真数大于零列不等式组,解得结果.
【详解】由题意得 ,
故答案为:
【点睛】本题考查函数定义域,考查基本分析求解能力,属基础题.
6.(2015·重庆·高考真题)函数 的定义域是
A.
B.
C.
D.
【答案】D
【详解】由 解得 或 ,故选D.
考点:函数的定义域与二次不等式.
7.(2015·四川·高考真题)设 , 都是不等于 的正数,则“ ”是“ ”的A.充要条件 B.充分不必要条件
C.必要不充分条件 D.既不充分也不必要条件
【答案】B
【详解】若 ,则 ,从而有 ,故为充分条件. 若 不一定有
,比如. ,从而 不成立.故选B.
考点:命题与逻辑.
8.(2015·湖北·高考真题)函数 的定义域为( )
A. B.
C. D.
【答案】C
【分析】根据根号下非负及真数大于零可得函数的定义域.
【详解】由函数 的表达式可知,函数 的定义域应满足条件:
,解之得 ,
即函数 的定义域为 ,
故选:C.
9.(2015·北京·高考真题)如图,函数 的图象为折线 ,则不等式 的解集是
A. B.
C. D.
【答案】C
【详解】试题分析:如下图所示,画出 的函数图象,从而可知交点 ,∴不等式
的解集为 ,故选C.考点:1.对数函数的图象;2.函数与不等式;3.数形结合的数学思想.
考点04 幂函数
1.(2024·天津·高考真题)设 ,则“ ”是“ ”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
【答案】C
【分析】说明二者与同一个命题等价,再得到二者等价,即是充分必要条件.
【详解】根据立方的性质和指数函数的性质, 和 都当且仅当 ,所以二者互为充要条件.
故选:C.
2.(2023·北京·高考真题)下列函数中,在区间 上单调递增的是( )
A. B.
C. D.
【答案】C
【分析】利用基本初等函数的单调性,结合复合函数的单调性判断ABC,举反例排除D即可.
【详解】对于A,因为 在 上单调递增, 在 上单调递减,
所以 在 上单调递减,故A错误;
对于B,因为 在 上单调递增, 在 上单调递减,
所以 在 上单调递减,故B错误;
对于C,因为 在 上单调递减, 在 上单调递减,
所以 在 上单调递增,故C正确;
对于D,因为 , ,
显然 在 上不单调,D错误.故选:C.
3.(2020·江苏·高考真题)已知y=f(x)是奇函数,当x≥0时, ,则f(-8)的值是 .
【答案】
【分析】先求 ,再根据奇函数求
【详解】 ,因为 为奇函数,所以
故答案为:
【点睛】本题考查根据奇函数性质求函数值,考查基本分析求解能力,属基础题.
考点05 指对幂函数值大小比较
1.(2024·天津·高考真题)若 ,则 的大小关系为( )
A. B. C. D.
【答案】B
【分析】利用指数函数和对数函数的单调性分析判断即可.
【详解】因为 在 上递增,且 ,
所以 ,
所以 ,即 ,
因为 在 上递增,且 ,
所以 ,即 ,
所以 ,
故选:B
2.(2023·全国甲卷·高考真题)已知函数 .记 ,则
( )
A. B. C. D.
【答案】A
【分析】利用作差法比较自变量的大小,再根据指数函数的单调性及二次函数的性质判断即可.
【详解】令 ,则 开口向下,对称轴为 ,
因为 ,而 ,
所以 ,即由二次函数性质知 ,
因为 ,而 ,
即 ,所以 ,
综上, ,
又 为增函数,故 ,即 .
故选:A.
3.(2023·天津·高考真题)设 ,则 的大小关系为( )
A. B.
C. D.
【答案】D
【分析】根据对应幂、指数函数的单调性判断大小关系即可.
【详解】由 在R上递增,则 ,
由 在 上递增,则 .
所以 .
故选:D
4.(2022·天津·高考真题)已知 , , ,则( )
A. B. C. D.
【答案】C
【分析】利用幂函数、对数函数的单调性结合中间值法可得出 、 、 的大小关系.
【详解】因为 ,故 .
故答案为:C.
5.(2022·全国甲卷·高考真题)已知 ,则( )
A. B. C. D.
【答案】A
【分析】法一:根据指对互化以及对数函数的单调性即可知 ,再利用基本不等式,换底公式
可得 , ,然后由指数函数的单调性即可解出.
【详解】[方法一]:(指对数函数性质)由 可得 ,而 ,所以 ,
即 ,所以 .
又 ,所以 ,即 ,
所以 .综上, .
[方法二]:【最优解】(构造函数)
由 ,可得 .
根据 的形式构造函数 ,则 ,
令 ,解得 ,由 知 .
在 上单调递增,所以 ,即 ,
又因为 ,所以 .
故选:A.
【点评】法一:通过基本不等式和换底公式以及对数函数的单调性比较,方法直接常用,属于通性通法;
法二:利用 的形式构造函数 ,根据函数的单调性得出大小关系,简单明了,是该
题的最优解.
6.(2022·全国新Ⅰ卷·高考真题)设 ,则( )
A. B. C. D.
【答案】C
【分析】构造函数 , 导数判断其单调性,由此确定 的大小.
【详解】方法一:构造法
设 ,因为 ,
当 时, ,当 时 ,
所以函数 在 单调递减,在 上单调递增,
所以 ,所以 ,故 ,即 ,
所以 ,所以 ,故 ,所以 ,
故 ,
设 ,则 ,
令 , ,当 时, ,函数 单调递减,
当 时, ,函数 单调递增,
又 ,
所以当 时, ,
所以当 时, ,函数 单调递增,
所以 ,即 ,所以
故选:C.
方法二:比较法
解: , , ,
① ,
令
则 ,
故 在 上单调递减,
可得 ,即 ,所以 ;
② ,
令
则 ,
令 ,所以 ,
所以 在 上单调递增,可得 ,即 ,
所以 在 上单调递增,可得 ,即 ,所以
故
7.(2021·天津·高考真题)设 ,则a,b,c的大小关系为( )
A. B. C. D.
【答案】D
【分析】根据指数函数和对数函数的性质求出 的范围即可求解.
【详解】 , ,
, ,
, ,
.故选:D.
8.(2021·全国新Ⅱ卷·高考真题)已知 , , ,则下列判断正确的是( )
A. B. C. D.
【答案】C
【分析】对数函数的单调性可比较 、 与 的大小关系,由此可得出结论.
【详解】 ,即 .
故选:C.
9.(2020·天津·高考真题)设 ,则 的大小关系为( )
A. B. C. D.
【答案】D
【分析】利用指数函数与对数函数的性质,即可得出 的大小关系.
【详解】因为 ,
,
,
所以 .
故选:D.
【点睛】本题考查的是有关指数幂和对数值的比较大小问题,在解题的过程中,注意应用指数函数和对数
函数的单调性,确定其对应值的范围.
比较指对幂形式的数的大小关系,常用方法:
(1)利用指数函数的单调性: ,当 时,函数递增;当 时,函数递减;
(2)利用对数函数的单调性: ,当 时,函数递增;当 时,函数递减;
(3)借助于中间值,例如:0或1等.
10.(2020·全国·高考真题)已知55<84,134<85.设a=log 3,b=log 5,c=log 8,则( )
5 8 13
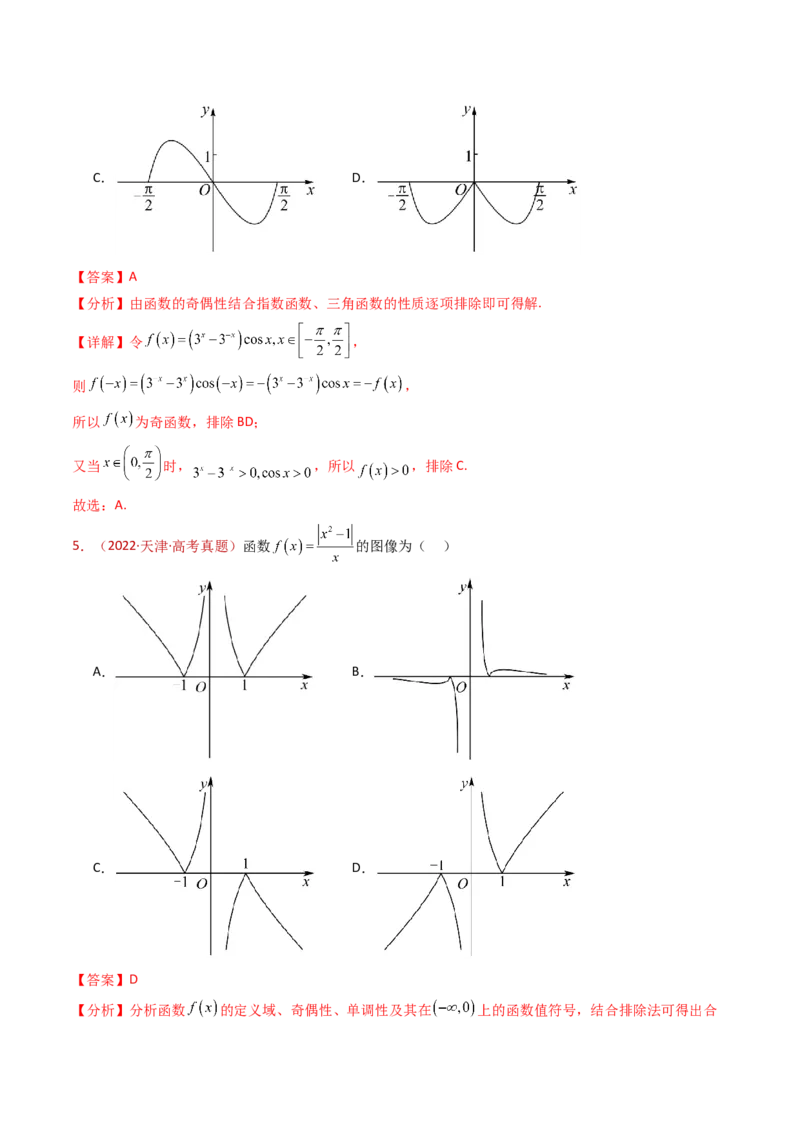
A.a2,排除A、C;
当x→+∞时,y→+∞,排除B.
故选:D.
【点睛】本题考查了函数图象的识别,抓住函数图象的差异是解题关键,属于基础题.
15.(2015·安徽·高考真题)函数 的图象如图所示,则下列结论成立的是
A. , ,
B. , ,
C. , ,
D. , ,
【答案】C
【详解】试题分析:函数在 处无意义,由图像看 在 轴右侧,所以 , ,
由 即 ,即函数的零点 ,故选C.
考点:函数的图像
16.(2015·浙江·高考真题)函数 ( 且 )的图象可能为( )
A. B.C. D.
【答案】D
【详解】因为 ,故函数是奇函数,所以排除A,B;取 ,
则 ,故选D.
考点:1.函数的基本性质;2.函数的图象.
考点07 函数零点及其应用
一、单选题
1.(2024·全国新Ⅰ卷·高考真题)当 时,曲线 与 的交点个数为( )
A.3 B.4 C.6 D.8
【答案】C
【分析】画出两函数在 上的图象,根据图象即可求解
【详解】因为函数 的的最小正周期为 ,
函数 的最小正周期为 ,
所以在 上函数 有三个周期的图象,
在坐标系中结合五点法画出两函数图象,如图所示:
由图可知,两函数图象有6个交点.
故选:C
2.(2024·全国新Ⅱ卷·高考真题)设函数 , ,当 时,曲线
与 恰有一个交点,则 ( )A. B. C.1 D.2
【答案】D
【分析】解法一:令 ,分析可知曲线 与 恰有一个交点,结合
偶函数的对称性可知该交点只能在y轴上,即可得 ,并代入检验即可;解法二:令
,可知 为偶函数,根据偶函数的对称性可知 的零点只能为0,即可
得 ,并代入检验即可.
【详解】解法一:令 ,即 ,可得 ,
令 ,
原题意等价于当 时,曲线 与 恰有一个交点,
注意到 均为偶函数,可知该交点只能在y轴上,
可得 ,即 ,解得 ,
若 ,令 ,可得
因为 ,则 ,当且仅当 时,等号成立,
可得 ,当且仅当 时,等号成立,
则方程 有且仅有一个实根0,即曲线 与 恰有一个交点,
所以 符合题意;
综上所述: .
解法二:令 ,
原题意等价于 有且仅有一个零点,
因为 ,
则 为偶函数,
根据偶函数的对称性可知 的零点只能为0,
即 ,解得 ,
若 ,则 ,
又因为 当且仅当 时,等号成立,
可得 ,当且仅当 时,等号成立,
即 有且仅有一个零点0,所以 符合题意;
故选:D.3.(2024·全国新Ⅱ卷·高考真题)(多选)对于函数 和 ,下列说法中正确的
有( )
A. 与 有相同的零点 B. 与 有相同的最大值
C. 与 有相同的最小正周期 D. 与 的图象有相同的对称轴
【答案】BC
【分析】根据正弦函数的零点,最值,周期公式,对称轴方程逐一分析每个选项即可.
【详解】A选项,令 ,解得 ,即为 零点,
令 ,解得 ,即为 零点,
显然 零点不同,A选项错误;
B选项,显然 ,B选项正确;
C选项,根据周期公式, 的周期均为 ,C选项正确;
D选项,根据正弦函数的性质 的对称轴满足 ,
的对称轴满足 ,
显然 图像的对称轴不同,D选项错误.
故选:BC
4.(2021·天津·高考真题)设 ,函数 ,若 在区间 内恰
有6个零点,则a的取值范围是( )
A. B.
C. D.
【答案】A
【分析】由 最多有2个根,可得 至少有4个根,分别讨论当
和 时两个函数零点个数情况,再结合考虑即可得出.
【详解】 最多有2个根,所以 至少有4个根,
由 可得 ,由 可得 ,
(1) 时,当 时, 有4个零点,即 ;
当 , 有5个零点,即 ;
当 , 有6个零点,即 ;
(2)当 时, ,
,
当 时, , 无零点;
当 时, , 有1个零点;
当 时,令 ,则 ,此时 有2个零点;
所以若 时, 有1个零点.
综上,要使 在区间 内恰有6个零点,则应满足
或 或 ,
则可解得a的取值范围是 .
【点睛】关键点睛:解决本题的关键是分成 和 两种情况分别讨论两个函数的零点个数情况.
5.(2020·天津·高考真题)已知函数 若函数 恰有4个零
点,则 的取值范围是( )
A. B.
C. D.
【答案】D
【分析】由 ,结合已知,将问题转化为 与 有 个不同交点,分
三种情况,数形结合讨论即可得到答案.【详解】注意到 ,所以要使 恰有4个零点,只需方程 恰有3个实根
即可,
令 ,即 与 的图象有 个不同交点.
因为 ,
当 时,此时 ,如图1, 与 有 个不同交点,不满足题意;
当 时,如图2,此时 与 恒有 个不同交点,满足题意;
当 时,如图3,当 与 相切时,联立方程得 ,
令 得 ,解得 (负值舍去),所以 .
综上, 的取值范围为 .
故选:D.
【点晴】本题主要考查函数与方程的应用,考查数形结合思想,转化与化归思想,是一道中档题.
6.(2019·全国·高考真题)函数 在 的零点个数为
A.2 B.3 C.4 D.5
【答案】B
【解析】令 ,得 或 ,再根据x的取值范围可求得零点.
【详解】由 ,得 或 , ,
.
在 的零点个数是3,
故选B.
【点睛】本题考查在一定范围内的函数的零点个数,渗透了直观想象和数学运算素养.采取特殊值法,利
用数形结合和方程思想解题.
7.(2019·浙江·高考真题)已知 ,函数 ,若函数
恰有三个零点,则
A. B.
C. D.
【答案】C
【分析】当 时, 最多一个零点;当 时,
,利用导数研究函数的单调性,根据单
调性画函数草图,根据草图可得.
【详解】当 时, ,得 ; 最多一个
零点;
当 时, ,
,
当 ,即 时, , 在 , 上递增, 最多一个零点.不
合题意;
当 ,即 时,令 得 , ,函数递增,令 得 , ,函数递减;函
数最多有2个零点;
根据题意函数 恰有3个零点 函数 在 上有一个零点,在 ,
上有2个零点,
如图:
且 ,
解得 , , .
故选 .【点睛】遇到此类问题,不少考生会一筹莫展.由于方程中涉及 两个参数,故按“一元化”想法,逐步
分类讨论,这一过程中有可能分类不全面、不彻底.
8.(2014·北京·高考真题)已知函数 ,在下列区间中,包含 零点的区间是
A. B. C. D.
【答案】C
【详解】因为 , ,所以由根的存在性定理可知:选C.
考点:本小题主要考查函数的零点知识,正确理解零点定义及根的存在性定理是解答好本类题目的关键.
9.(2018·全国·高考真题)已知函数 .若g(x)存在2个零点,
则a的取值范围是
A.[–1,0) B.[0,+∞) C.[–1,+∞) D.[1,+∞)
【答案】C
【详解】分析:首先根据g(x)存在2个零点,得到方程 有两个解,将其转化为
有两个解,即直线 与曲线 有两个交点,根据题中所给的函数解析式,画出函
数 的图像(将 去掉),再画出直线 ,并将其上下移动,从图中可以发现,当 时,
满足 与曲线 有两个交点,从而求得结果.
详解:画出函数 的图像, 在y轴右侧的去掉,
再画出直线 ,之后上下移动,
可以发现当直线过点A时,直线与函数图像有两个交点,
并且向下可以无限移动,都可以保证直线与函数的图像有两个交点,
即方程 有两个解,
也就是函数 有两个零点,
此时满足 ,即 ,故选C.点睛:该题考查的是有关已知函数零点个数求有关参数的取值范围问题,在求解的过程中,解题的思路是
将函数零点个数问题转化为方程解的个数问题,将式子移项变形,转化为两条曲线交点的问题,画出函数
的图像以及相应的直线,在直线移动的过程中,利用数形结合思想,求得相应的结果.
10.(2017·山东·高考真题)已知当 时,函数 的图象与 的图象有且只有
一个交点,则正实数m的取值范围是
A. B.
C. D.
【答案】B
【详解】当 时, , 单调递减,且 , 单
调递增,且 ,此时有且仅有一个交点;当 时, ,
在 上单调递增,所以要有且仅有一个交点,需 选B.
【名师点睛】已知函数有零点求参数取值范围常用的方法和思路
(1)直接法:直接根据题设条件构建关于参数的不等式,再通过解不等式确定参数范围;
(2)分离参数法:先将参数分离,转化成求函数值域问题加以解决;
(3)数形结合法:先对解析式变形,在同一平面直角坐标系中,画出函数的图象,然后数形结
合求解.
11.(2016·天津·高考真题)已知函数 , .若 在区间
内没有零点,则 的取值范围是
A. B.
C. D.
【答案】D
【详解】, ,
所以 ,
因此 ,
选:D.
12.(2016·天津·高考真题)已知函数 ( ,且 )在 上单调递减,
且关于x的方程 恰有两个不相等的实数解,则 的取值范围是
A. B.[ , ] C.[ , ] { } D.[ , ) { }
【答案】C
【详解】试题分析:由 在 上单调递减可知 ,由方程 恰好有两个不
相等的实数解,可知 , ,又 时,抛物线 与直线 相切,
也符合题意,∴实数 的取值范围是 ,故选C.
【考点】函数性质综合应用
【名师点睛】已知函数有零点求参数取值范围常用的方法和思路:
(1)直接法:直接根据题设条件构建关于参数的不等式,再通过解不等式确定参数范围;
(2)分离参数法:先将参数分离,转化成求函数值域问题加以解决;
(3)数形结合法:先对解析式变形,在同一平面直角坐标系中,画出函数的图象,然后数形结合求解.
13.(2016·天津·高考真题)已知函数 , .若 在区间 内
没有零点,则 的取值范围是
A. B. C. D.
【答案】D
【分析】先把 化成 ,求出 的零点的一般形式为 ,根据
在区间 内没有零点可得关于 的不等式组,结合 为整数可得其相应的取值,从而得到所求的
取值范围.【详解】由题设有 ,
令 ,则有 即 .
因为 在区间 内没有零点,
故存在整数 ,使得 ,
即 ,因为 ,所以 且 ,故 或 ,
所以 或 ,
故选:D.
【点睛】本题考查三角函数在给定范围上的零点的存在性问题,此类问题可转化为不等式组的整数解问题,
本题属于难题.
14.(2015·天津·高考真题)已知函数 ,函数 ,则函数
的零点的个数为
A.2 B.3 C.4 D.5
【答案】A
【详解】当 时 ,所以 , ,此时函数
的小于零的零点为 ;当 时
, ,函数 无零点;当 时,
, ,函数 大于2的零点为
,综上可得函数 的零点的个数为2.故选A.
考点:本题主要考查分段函数、函数零点及学生分析问题解决问题的能力.
15.(2015·天津·高考真题)已知函数 ,函数 ,其中 ,若
函数 恰有4个零点,则 的取值范围是( )A. B. C. D.
【答案】D
【详解】函数 恰有4个零点,即方程 ,
即 有4个不同的实数根,
即直线 与函数 的图象有四个不同的交点.
又
做出该函数的图象如图所示,
由图得,当 时,直线 与函数 的图象有4个不同的交点,
故函数 恰有4个零点时,
b的取值范围是 故选D.
考点:1、分段函数;2、函数的零点.
【方法点晴】本题主要考查的是分段函数和函数的零点,属于难题.已知函数的零点个数,一般利用数形
结合思想转化为两个函数的图像的交点个数问题,作图时一定要保证图形准确, 否则很容易出现错误.
16.(2015·安徽·高考真题)下列函数中,既是偶函数又存在零点的是
A. B. C. D.
【答案】A
【详解】由选项可知, 项均不是偶函数,故排除 , 项是偶函数,但 项与 轴没有交点,即
项的函数不存在零点,故选A.
考点:1.函数的奇偶性;2.函数零点的概念.二、填空题
17.(2024·全国甲卷·高考真题)曲线 与 在 上有两个不同的交点,则 的
取值范围为 .
【答案】
【分析】将函数转化为方程,令 ,分离参数 ,构造新函数 结合
导数求得 单调区间,画出大致图形数形结合即可求解.
【详解】令 ,即 ,令
则 ,令 得 ,
当 时, , 单调递减,
当 时, , 单调递增, ,
因为曲线 与 在 上有两个不同的交点,
所以等价于 与 有两个交点,所以 .
故答案为:
18.(2024·天津·高考真题)若函数 恰有一个零点,则 的取值范围为 .
【答案】
【分析】结合函数零点与两函数的交点的关系,构造函数 与 ,则两函
数图象有唯一交点,分 、 与 进行讨论,当 时,计算函数定义域可得 或 ,计
算可得 时,两函数在 轴左侧有一交点,则只需找到当 时,在 轴右侧无交点的情况即
可得;当 时,按同一方式讨论即可得.
【详解】令 ,即 ,由题可得 ,
当 时, ,有 ,则 ,不符合要求,舍去;
当 时,则 ,
即函数 与函数 有唯一交点,
由 ,可得 或 ,
当 时,则 ,则 ,
即 ,整理得 ,
当 时,即 ,即 ,
当 , 或 (正值舍去),
当 时, 或 ,有两解,舍去,
即当 时, 在 时有唯一解,
则当 时, 在 时需无解,
当 ,且 时,
由函数 关于 对称,令 ,可得 或 ,
且函数 在 上单调递减,在 上单调递增,
令 ,即 ,
故 时, 图象为双曲线 右支的 轴上方部分向右平移 所得,由 的渐近线方程为 ,
即 部分的渐近线方程为 ,其斜率为 ,
又 ,即 在 时的斜率 ,
令 ,可得 或 (舍去),
且函数 在 上单调递增,
故有 ,解得 ,故 符合要求;
当 时,则 ,
即函数 与函数 有唯一交点,
由 ,可得 或 ,
当 时,则 ,则 ,
即 ,整理得 ,
当 时,即 ,即 ,
当 , (负值舍去)或 ,
当 时, 或 ,有两解,舍去,
即当 时, 在 时有唯一解,
则当 时, 在 时需无解,
当 ,且 时,由函数 关于 对称,令 ,可得 或 ,
且函数 在 上单调递减,在 上单调递增,
同理可得: 时, 图象为双曲线 左支的 轴上方部分向左平移 所得,
部分的渐近线方程为 ,其斜率为 ,
又 ,即 在 时的斜率 ,
令 ,可得 或 (舍去),
且函数 在 上单调递减,
故有 ,解得 ,故 符合要求;
综上所述, .
故答案为: .
【点睛】关键点点睛:本题关键点在于将函数 的零点问题转化为函数 与函数
的交点问题,从而可将其分成两个函数研究.
19.(2023·天津·高考真题)设 ,函数 ,若 恰有两个零点,则 的取值
范围为 .
【答案】
【分析】根据绝对值的意义,去掉绝对值,求出零点,再根据根存在的条件即可判断 的取值范围.
【详解】(1)当 时, ,
即 ,
若 时, ,此时 成立;若 时, 或 ,
若方程有一根为 ,则 ,即 且 ;
若方程有一根为 ,则 ,解得: 且 ;
若 时, ,此时 成立.
(2)当 时, ,
即 ,
若 时, ,显然 不成立;
若 时, 或 ,
若方程有一根为 ,则 ,即 ;
若方程有一根为 ,则 ,解得: ;
若 时, ,显然 不成立;
综上,
当 时,零点为 , ;
当 时,零点为 , ;
当 时,只有一个零点 ;
当 时,零点为 , ;
当 时,只有一个零点 ;
当 时,零点为 , ;
当 时,零点为 .
所以,当函数有两个零点时, 且 .
故答案为: .
【点睛】本题的解题关键是根据定义去掉绝对值,求出方程的根,再根据根存在的条件求出对应的范围,
然后根据范围讨论根(或零点)的个数,从而解出.
20.(2023·全国新Ⅰ卷·高考真题)已知函数 在区间 有且仅有3个零点,则
的取值范围是 .【答案】
【分析】令 ,得 有3个根,从而结合余弦函数的图像性质即可得解.
【详解】因为 ,所以 ,
令 ,则 有3个根,
令 ,则 有3个根,其中 ,
结合余弦函数 的图像性质可得 ,故 ,
故答案为: .
21.(2022·天津·高考真题)设 ,对任意实数x,记 .若 至少
有3个零点,则实数 的取值范围为 .
【答案】
【分析】设 , ,分析可知函数 至少有一个零点,可得出 ,求出
的取值范围,然后对实数 的取值范围进行分类讨论,根据题意可得出关于实数 的不等式,综合可求
得实数 的取值范围.
【详解】设 , ,由 可得 .
要使得函数 至少有 个零点,则函数 至少有一个零点,则 ,
解得 或 .
①当 时, ,作出函数 、 的图象如下图所示:
此时函数 只有两个零点,不合乎题意;
②当 时,设函数 的两个零点分别为 、 ,
要使得函数 至少有 个零点,则 ,所以, ,解得 ;
③当 时, ,作出函数 、 的图象如下图所示:
由图可知,函数 的零点个数为 ,合乎题意;
④当 时,设函数 的两个零点分别为 、 ,
要使得函数 至少有 个零点,则 ,
可得 ,解得 ,此时 .
综上所述,实数 的取值范围是 .
故答案为: .
【点睛】方法点睛:已知函数有零点(方程有根)求参数值(取值范围)常用的方法:
(1)直接法:直接求解方程得到方程的根,再通过解不等式确定参数范围;
(2)分离参数法:先将参数分离,转化成求函数的值域问题加以解决;
(3)数形结合法:先对解析式变形,进而构造两个函数,然后在同一平面直角坐标系中画出函数的图象,
利用数形结合的方法求解.
22.(2022·北京·高考真题)若函数 的一个零点为 ,则 ;
.
【答案】 1
【分析】先代入零点,求得A的值,再将函数化简为 ,代入自变量 ,计算即可.
【详解】∵ ,∴
∴故答案为:1,
23.(2021·北京·高考真题)已知函数 ,给出下列四个结论:
①若 , 恰 有2个零点;
②存在负数 ,使得 恰有1个零点;
③存在负数 ,使得 恰有3个零点;
④存在正数 ,使得 恰有3个零点.
其中所有正确结论的序号是 .
【答案】①②④
【分析】由 可得出 ,考查直线 与曲线 的左、右支分别相切的情
形,利用方程思想以及数形结合可判断各选项的正误.
【详解】对于①,当 时,由 ,可得 或 ,①正确;
对于②,考查直线 与曲线 相切于点 ,
对函数 求导得 ,由题意可得 ,解得 ,
所以,存在 ,使得 只有一个零点,②正确;
对于③,当直线 过点 时, ,解得 ,
所以,当 时,直线 与曲线 有两个交点,
若函数 有三个零点,则直线 与曲线 有两个交点,
直线 与曲线 有一个交点,所以, ,此不等式无解,
因此,不存在 ,使得函数 有三个零点,③错误;
对于④,考查直线 与曲线 相切于点 ,
对函数 求导得 ,由题意可得 ,解得 ,
所以,当 时,函数 有三个零点,④正确.故答案为:①②④.
【点睛】思路点睛:已知函数的零点或方程的根的情况,求解参数的取值范围问题的本质都是研究函数的
零点问题,求解此类问题的一般步骤:
(1)转化,即通过构造函数,把问题转化成所构造函数的零点问题;
(2)列式,即根据函数的零点存在定理或结合函数的图象列出关系式;
(3)得解,即由列出的式子求出参数的取值范围.
24.(2019·江苏·高考真题)设 是定义在 上的两个周期函数, 的周期为4, 的周期为
2,且 是奇函数.当 时, , ,其中 .若在区间
上,关于 的方程 有8个不同的实数根,则 的取值范围是 .
【答案】 .
【分析】分别考查函数 和函数 图像的性质,考查临界条件确定k的取值范围即可.
【详解】当 时, 即
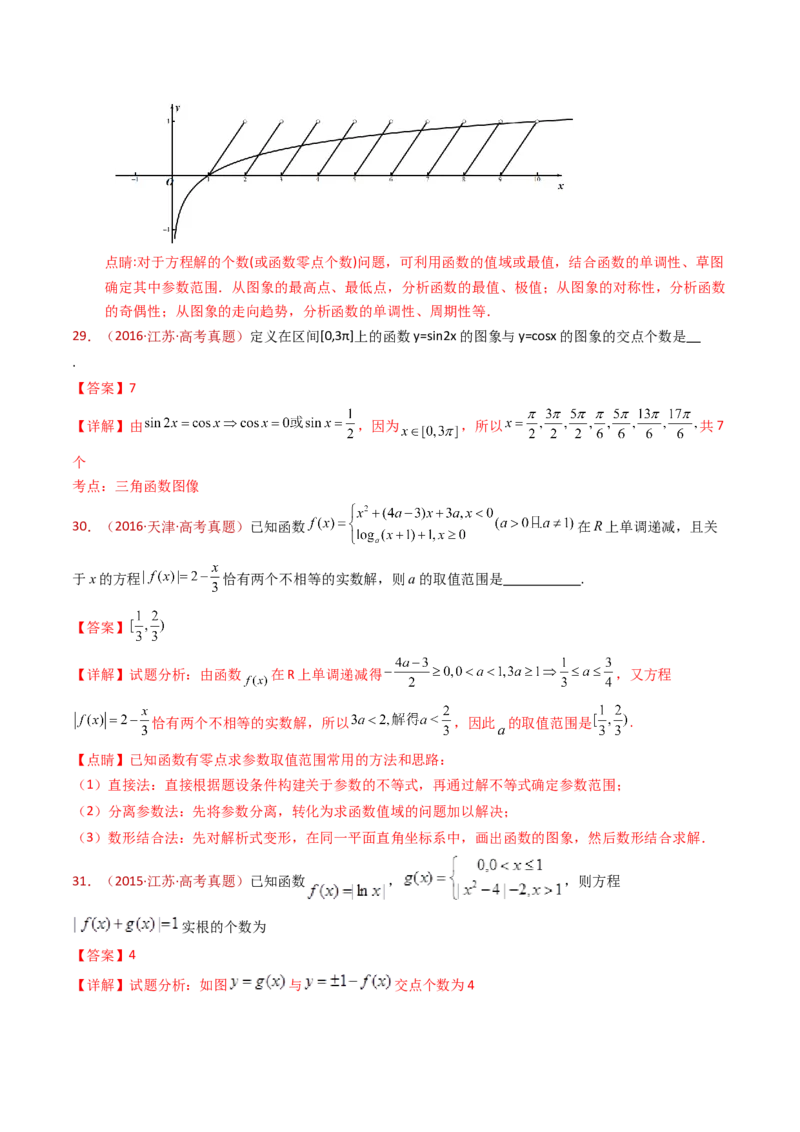
又 为奇函数,其图象关于原点对称,其周期为 ,如图,函数 与 的图象,要使 在
上有 个实根,只需二者图象有 个交点即可.
当 时,函数 与 的图象有 个交点;
当 时, 的图象为恒过点 的直线,只需函数 与 的图象有 个交点.当
与 图象相切时,圆心 到直线 的距离为 ,即 ,得 ,函数 与
的图象有 个交点;当 过点 时,函数 与 的图象有 个交点,此时 ,
得 .综上可知,满足 在 上有 个实根的 的取值范围为 .
【点睛】本题考点为参数的取值范围,侧重函数方程的多个实根,难度较大.不能正确画出函数图象的交点
而致误,根据函数的周期性平移图象,找出两个函数图象相切或相交的临界交点个数,从而确定参数的取
值范围.
25.(2018·全国·高考真题)函数 在 的零点个数为 .
【答案】
【分析】方法一:求出 的范围,再由函数值为零,得到 的取值即得零点个数.
【详解】[方法一]:【最优解】
由题可知 ,或
解得 ,或 故有3个零点.
故答案为: .
方法二:
令 ,即 ,解得, ,分别令 ,得
,所以函数 在 的零点的个数为3.
故答案为: .
【整体点评】方法一:先求出 的范围,再根据余弦函数在该范围内的零点,从而解出,是该题的最
优解;
方法二:先求出函数的所有零点,再根据题中范围限制,找出符合题意的零点.
26.(2018·浙江·高考真题)已知λ∈R,函数f(x)= ,当λ=2时,不等式f(x)<0的解集是
.若函数f(x)恰有2个零点,则λ的取值范围是 .
【答案】 (1,4)
【详解】分析:根据分段函数,转化为两个不等式组,分别求解,最后求并集.先讨论一次函数零点的取法,
再对应确定二次函数零点的取法,即得参数 的取值范围.
详解:由题意得 或 ,所以 或 ,即 ,不等式f(x)<0的解集
是当 时, ,此时 ,即在 上有两个零点;当 时,
,由 在 上只能有一个零点得 .综上, 的取值范围为
.
点睛:已知函数有零点求参数取值范围常用的方法和思路:
(1)直接法:直接根据题设条件构建关于参数的不等式,再通过解不等式确定参数范围;
(2)分离参数法:先将参数分离,转化成求函数值域问题加以解决;
(3)数形结合法:先对解析式变形,在同一平面直角坐标系中,画出函数的图象,然后数形结合求解.
27.(2018·天津·高考真题)已知 ,函数 若关于 的方程 恰有2
个互异的实数解,则 的取值范围是 .
【答案】
【详解】分析:由题意分类讨论 和 两种情况,然后绘制函数图像,数形结合即可求得最终结果.
详解:分类讨论:当 时,方程 即 ,
整理可得: ,
很明显 不是方程的实数解,则 ,
当 时,方程 即 ,
整理可得: ,
很明显 不是方程的实数解,则 ,
令 ,
其中 ,
原问题等价于函数 与函数 有两个不同的交点,求 的取值范围.
结合对勾函数和函数图象平移的规律绘制函数 的图象,
同时绘制函数 的图象如图所示,考查临界条件,
结合 观察可得,实数 的取值范围是 .点睛:本题的核心在考查函数的零点问题,函数零点的求解与判断方法包括:
(1)直接求零点:令f(x)=0,如果能求出解,则有几个解就有几个零点.
(2)零点存在性定理:利用定理不仅要函数在区间[a,b]上是连续不断的曲线,且f(a)·f(b)<0,还必须结合函
数的图象与性质(如单调性、奇偶性)才能确定函数有多少个零点.
(3)利用图象交点的个数:将函数变形为两个函数的差,画两个函数的图象,看其交点的横坐标有几个不同
的值,就有几个不同的零点.
28.(2017·江苏·高考真题)设 是定义在R 且周期为1的函数,在区间 上, 其
中集合 ,则方程 的解的个数是
【答案】8
【详解】由于 ,则需考虑 的情况,
在此范围内, 且 时,设 ,且 互质,
若 ,则由 ,可设 ,且 互质,
因此 ,则 ,此时左边为整数,右边为非整数,矛盾,因此 ,
因此 不可能与每个周期内 对应的部分相等,
只需考虑 与每个周期 的部分的交点,
画出函数图象,图中交点除外 其他交点横坐标均为无理数,属于每个周期 的部分,
且 处 ,则在 附近仅有一个交点,
因此方程 的解的个数为8.点睛:对于方程解的个数(或函数零点个数)问题,可利用函数的值域或最值,结合函数的单调性、草图
确定其中参数范围.从图象的最高点、最低点,分析函数的最值、极值;从图象的对称性,分析函数
的奇偶性;从图象的走向趋势,分析函数的单调性、周期性等.
29.(2016·江苏·高考真题)定义在区间[0,3π]上的函数y=sin2x的图象与y=cosx的图象的交点个数是
.
【答案】7
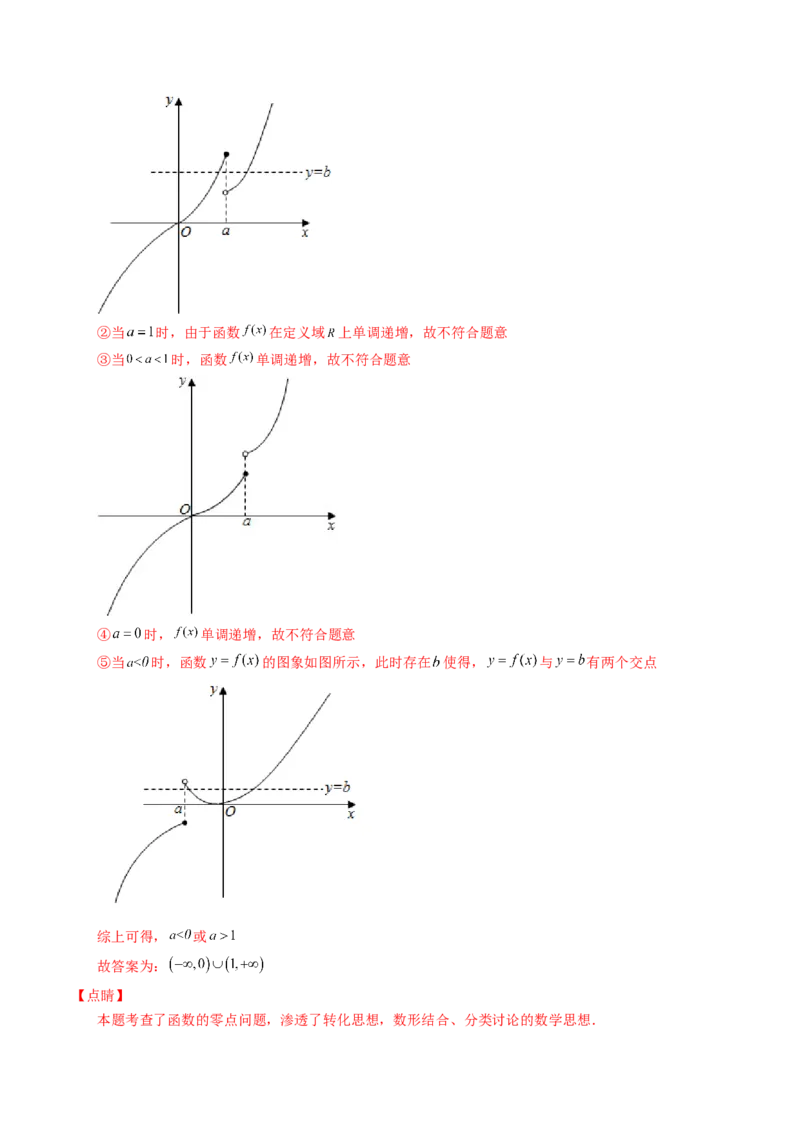
【详解】由 ,因为 ,所以 共7
个
考点:三角函数图像
30.(2016·天津·高考真题)已知函数 在R上单调递减,且关
于x的方程 恰有两个不相等的实数解,则a的取值范围是 .
【答案】
【详解】试题分析:由函数 在R上单调递减得 ,又方程
恰有两个不相等的实数解,所以 ,因此 的取值范围是 .
【点睛】已知函数有零点求参数取值范围常用的方法和思路:
(1)直接法:直接根据题设条件构建关于参数的不等式,再通过解不等式确定参数范围;
(2)分离参数法:先将参数分离,转化为求函数值域的问题加以解决;
(3)数形结合法:先对解析式变形,在同一平面直角坐标系中,画出函数的图象,然后数形结合求解.
31.(2015·江苏·高考真题)已知函数 , ,则方程
实根的个数为
【答案】4
【详解】试题分析:如图 与 交点个数为4考点:函数图像
【思路点睛】(1)运用函数图象解决问题时,先要正确理解和把握函数图象本身的含义及其表示的内容,
熟悉图象所能够表达的函数的性质.
(2)在研究函数性质特别是单调性、最值、零点时,要注意用好其与图象的关系,结合图象研究.
32.(2015·湖北·高考真题)函数 的零点个数为_________.
【答案】 .
【详解】函数 的零点个数等价于方程 的根的个数,
即函数 与 的图象交点个数.
于是,分别画出其函数图像如下图所示,由图可知,函数 与 的图象有2个交点.
33.(2015·湖北·高考真题)函数 的零点个数为 .
【答案】2
【详解】因为所以函数 的零点个数为函数 与 图象的交点的个数,
函数 与 图象如图,由图知,两函数图象有2个交点,
所以函数 有2个零点.
考点:二倍角的正弦、余弦公式,诱导公式,函数的零点.
34.(2015·安徽·高考真题)在平面直角坐标系 中,若直线 与函数 的图像只有一
个交点,则 的值为 .
【答案】
【详解】试题分析: 时 取得最小值 .即函数 的图像的最低点为 .
当 时,由数形结合可知此时直线 与 的图像必有两个交点,故舍;
当 时,要使直线 与 的图像只有一个交点,则有直线 必过点 ,
即 ,解得 .
综上可得 .
考点:1函数图像交点问题;2数形结合思想.
35.(2015·湖南·高考真题)已知 ,若存在实数 ,使函数 有两个零点,
则 的取值范围是 .
【答案】
【分析】由 有两个零点可得 有两个零点,即 与 的图象有两个交点,则
函数在定义域内不能是单调函数,结合函数图象可求 的范围
【详解】 有两个零点,
有两个零点,即 与 的图象有两个交点,
由 可得, 或
①当 时,函数 的图象如图所示,此时存在 ,满足题意,故 满足题意②当 时,由于函数 在定义域 上单调递增,故不符合题意
③当 时,函数 单调递增,故不符合题意
④ 时, 单调递增,故不符合题意
⑤当 时,函数 的图象如图所示,此时存在 使得, 与 有两个交点
综上可得, 或
故答案为:
【点睛】
本题考查了函数的零点问题,渗透了转化思想,数形结合、分类讨论的数学思想.36.(2015·湖南·高考真题)若函数 有两个零点,则实数 的取值范围是_____.
【答案】
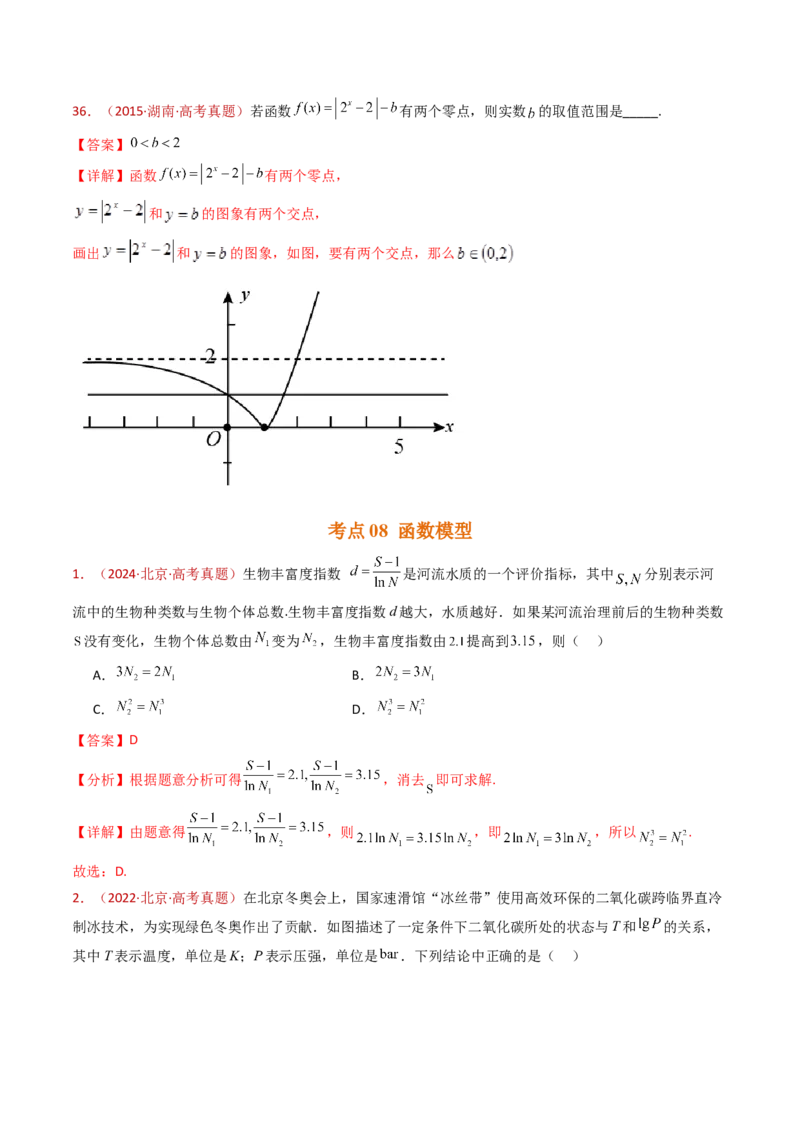
【详解】函数 有两个零点,
和 的图象有两个交点,
画出 和 的图象,如图,要有两个交点,那么
考点08 函数模型
1.(2024·北京·高考真题)生物丰富度指数 是河流水质的一个评价指标,其中 分别表示河
流中的生物种类数与生物个体总数.生物丰富度指数d越大,水质越好.如果某河流治理前后的生物种类数
没有变化,生物个体总数由 变为 ,生物丰富度指数由 提高到 ,则( )
A. B.
C. D.
【答案】D
【分析】根据题意分析可得 ,消去 即可求解.
【详解】由题意得 ,则 ,即 ,所以 .
故选:D.
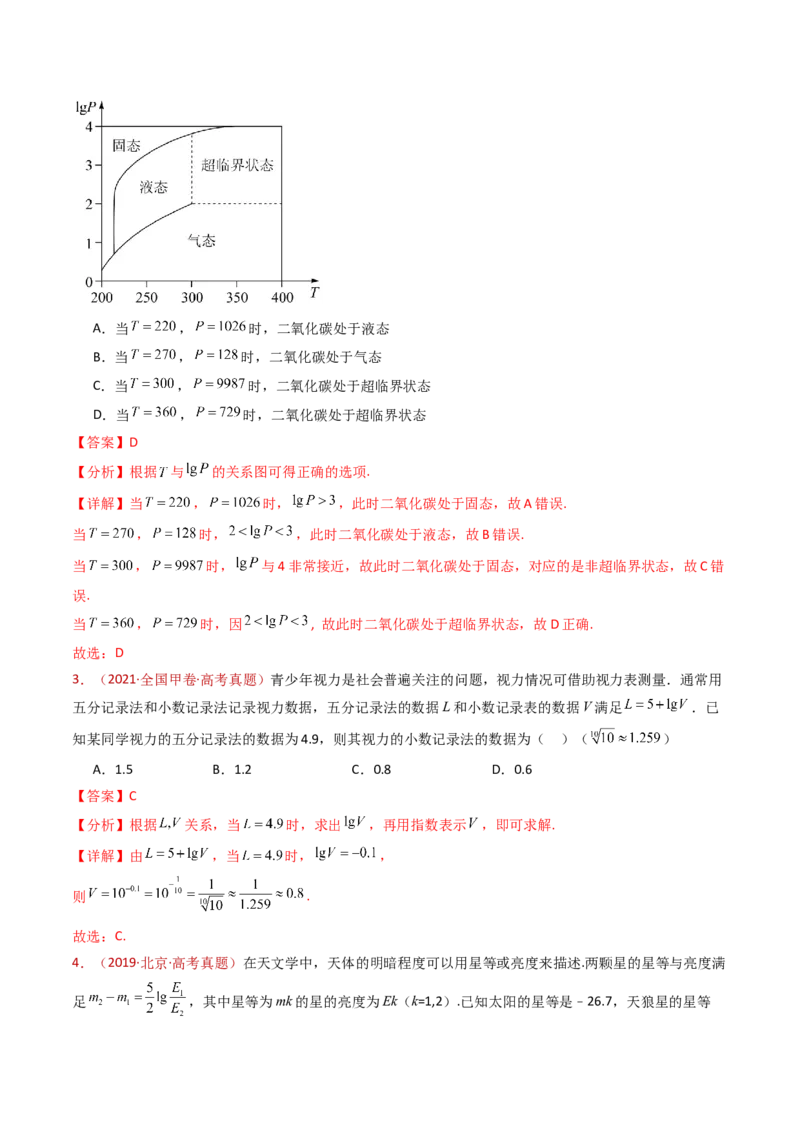
2.(2022·北京·高考真题)在北京冬奥会上,国家速滑馆“冰丝带”使用高效环保的二氧化碳跨临界直冷
制冰技术,为实现绿色冬奥作出了贡献.如图描述了一定条件下二氧化碳所处的状态与T和 的关系,
其中T表示温度,单位是K;P表示压强,单位是 .下列结论中正确的是( )A.当 , 时,二氧化碳处于液态
B.当 , 时,二氧化碳处于气态
C.当 , 时,二氧化碳处于超临界状态
D.当 , 时,二氧化碳处于超临界状态
【答案】D
【分析】根据 与 的关系图可得正确的选项.
【详解】当 , 时, ,此时二氧化碳处于固态,故A错误.
当 , 时, ,此时二氧化碳处于液态,故B错误.
当 , 时, 与4非常接近,故此时二氧化碳处于固态,对应的是非超临界状态,故C错
误.
当 , 时,因 , 故此时二氧化碳处于超临界状态,故D正确.
故选:D
3.(2021·全国甲卷·高考真题)青少年视力是社会普遍关注的问题,视力情况可借助视力表测量.通常用
五分记录法和小数记录法记录视力数据,五分记录法的数据L和小数记录表的数据V满足 .已
知某同学视力的五分记录法的数据为4.9,则其视力的小数记录法的数据为( )( )
A.1.5 B.1.2 C.0.8 D.0.6
【答案】C
【分析】根据 关系,当 时,求出 ,再用指数表示 ,即可求解.
【详解】由 ,当 时, ,
则 .
故选:C.
4.(2019·北京·高考真题)在天文学中,天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满
足 ,其中星等为mk的星的亮度为Ek(k=1,2).已知太阳的星等是–26.7,天狼星的星等是–1.45,则太阳与天狼星的亮度的比值为
A.1010.1 B.10.1 C.lg10.1 D.
【答案】A
【解析】由题意得到关于 的等式,结合对数的运算法则可得亮度的比值.
【详解】两颗星的星等与亮度满足 ,令 ,
.
故选A.
【点睛】本题以天文学问题为背景,考查考生的数学应用意识、信息处理能力、阅读理解能力以及指数对数运
算.
5.(2017·北京·高考真题)根据有关资料,围棋状态空间复杂度的上限M约为3361,而可观测宇宙中普通
物质的原子总数N约为1080.则下列各数中与 最接近的是
(参考数据:lg3≈0.48)
A.1033 B.1053
C.1073 D.1093
【答案】D
【详解】试题分析:设 ,两边取对数, ,
所以 ,即 最接近 ,故选D.
【名师点睛】本题考查了转化与化归能力,本题以实际问题的形式给出,但本质就是对数的运算关系,以
及指数与对数运算的关系,难点是令 ,并想到两边同时取对数进行求解,对数运算公式包含
, , .