广东省2025届高三数学一调模拟卷（答案）_8月_2408082025届广东省普通高中毕业班第一次调研考试_广东省高考研究会：广东省2025届高三数学一调模拟卷

2025 届广东省普通高中毕业班调研考试（一） 数 学参考答案与解析 一、选择题 会 1. 【答案】B 究 【解析】集合A={xZ|x2 −8x+150}={xZ|(x−3)(x−5)0}={3,4,5}. 研 而B={x|x5}，故AB={3,4}. 考 考察集合交集的定义. 高 2. 【答案】A 省 z z 【解析】z ，z 均为纯虚数可以推出 1 为实数， 1 为实数不可以推出z ，z 均为纯虚数，故为充分不必 1 2 z z 1 2 东2 2 要条件. 广 3． 【答案】C 2 2 3 【解析】(a 2b) b a b 2b a b cos150 2b 2 3 ( ) 2 2 ( 3)2 3 会 4. 【答案】B 究 2  1 3 【解析】由题干得 =sin(+ )−sin= sin+ 研cos−sin 3 3 2 2 考 3 1  = cos− sin=cos(+ ). 2 2 6 高   2 1 所以cos(2+ )=2cos2(+ )−1=2( )2 −1=− . 省 3 6 3 9 考察三角函数中两角和差公式以及倍角公式. 东 5. 广 【答案】C 【解析】 1 4 由a =aa aq=1a = ，S +T =122q+3+ =12， 2 1 3 1 1 q 3 3 q 11 则2q2 −9q+4=(2q−1)(q−4)=0q = ,q =4. 1 2 2 1 由于a 为递增数列，则q=4,a = ， n 1 4 会 所以a 的通项公式为a =4n−2 . n n 究 1 ( 1−4n) 1 所以S = 4 = ( 4n −1 ) . n 1−4 12 研 【考察】 （1）等比数列a ,q,a ,S ； 考 1 n n （2）转化、消元的数学思想 高 6. 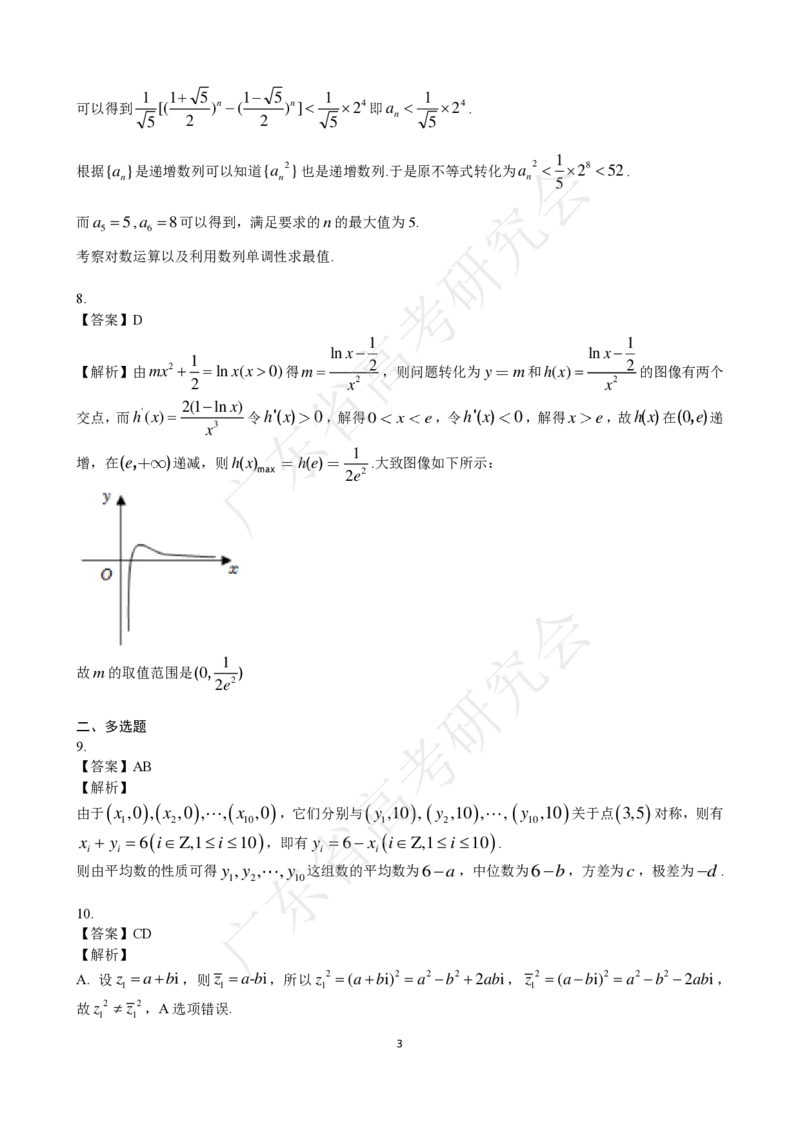【答案】A 省 【解析】 东 广 V =4 3 R= 3. 记侧棱长为l，球心到四棱锥顶点的距离为h. O h 3 h2 1 ( )2 会 则 =  = l2 −12=4h2(1)； h+ 3 +12=l2 −12(2) . l2 −12 2 3 l2 −12 4 究 ( )2 5 3 所以 h+ 3 +12=4h2 3h2 −2 3h−15=0h= . 3 研 1 5 3  128 3 所以V = 48 + 3= .   3  3  3 考 【考察】 （1）锥体、球体的体积公式； 高 （2）内切球与正四棱锥的几何关系. 省 7. 【答案】A 东 【解析】由题知n是log [(1+ 5)x −(1− 5)x] x+4的正整数解. 广2 化简log [(1+ 5)n −(1− 5)n]n+4有 2 (1+ 5)n −(1− 5)n 2n+4 . 21 1+ 5 1− 5 1 1 可以得到 [( )n −( )n] 24即a  24 . 5 2 2 5 n 5 会1 根据{a }是递增数列可以知道{a 2}也是递增数列.于是原不等式转化为a 2  28 52. n n n 5 究 而a =5,a =8可以得到，满足要求的n的最大值为5. 5 6 研 考察对数运算以及利用数列单调性求最值. 考 8. 【答案】D 高 1 1 lnx− lnx− 1 【解析】由mx2 + =lnx(x0)得省 m= 2 ，则问题转化为y m和h(x)= 2 的图像有两个 2 x2 x2 2(1−lnx) 交点，而h'(x)= 令东h'(x) 0，解得0 x e，令h'(x) 0，解得x e，故h(x)在(0,e)递 x3 1 增，在(e, )递减，广则h(x) h(e) .大致图像如下所示： max 2e2 会 究 1 故m的取值范围是(0, ) 2e2 研 二、多选题 考 9. 【答案】AB 高 【解析】 由于 (x ,0),(x ,0), ,(x ,0) ，它们分别与 (y ,10), (y ,10), , (y ,10) 关于点 (3,5) 对称，则有 1 2 10 省1 2 10 x + y =6(iZ,1i 10) ，即有 y =6−x (iZ,1i 10) . i i i i 东 则由平均数的性质可得 y ,y , ,y 这组数的平均数为6−a，中位数为6−b，方差为c，极差为−d . 1 2 10 广 10. 【答案】CD 【解析】 A. 设z =a+bi，则z =a-bi，所以z2 =(a+bi)2 =a2 −b2 +2abi，z2 =(a−bi)2 =a2 −b2 −2abi， 1 1 1 1 故z2  z2，A选项错误. 1 1 3B. 由复数的几何意义可知， z , z , z +z 在复平面表示向量OA,OB,OA+OB的模长.当OA,OB共线 1 2 1 2 时， OA + OB = OA+OB ，即 z +z = z + z ；当OA,OB不共线时，OA,OB,OA+OB分别表示 1 2 1 2 OAB三边长，根据三角形中两边之和大于第三边，可得 OA + OB 会OA+OB ，即 z +z  z + z . 1 2 1 2 因此， z +z  z + z ，B选项错误. 1 2 1 2 究 C. 由复数的几何意义可知，z −2−2i =2表示复数z 对应的点A到定点(2,2)的距离为2，即动点A的 1 1 轨迹是以(2,2)为圆心，2为半径的圆， z +1−6i 表示研点 A到定点 (−1,6) 的距离，由圆的性质可知， 1 z +1−6i = (−1−2)2 +(6−2)2 −2=3，C项正确. 1 max 考 D. 由复数的几何意义可知， z +i + z −i =4表示复数z 对应的点B到两定点(0,−1)、(0,1)的距离之 2 2 2 高 y2 x2 和为4，所以点B的轨迹为椭圆： + =1， z 表示点B到原点的距离，由椭圆的几何性质可得， 2 4 3 省 当点B在椭圆与x轴的交点上时，取得最小值，即 z = 3，D选项正确. 2 min 综上，故选：CD. 东 11. 广 【答案】ACD 【解析】 A. 令x=0，则有 f(e)−ef(e)=(1−e)f(e)=0，所以 f(e)=0，故A正确. B. 对 f(e+x)−ef(e−x)=0两边求导，得 f(e+x)+ef(e−x)=0，所以 f(e+x)=−ef(e−x)， 代入 f(e+x)+ f '(e−x)0，得当x0时，(1−e)f(e−x)0,所以 f(e−x)0.又因为 f(e+x)+ f '(e−x)0，所以， f(e+x)0. 会 因此，当xe时，f(x)0，f(x)在(−,e)上单调递减；当xe时，f(x)0，f(x)在(e，+) 上单调递增.故B错误. 究 C. 对x ,x ,e的大小关系进行分类讨论： 1 2 研 ①当x  x e时， f(x)在(−,e)上单调递减，所以 f(x )  f(x )，显然有x +x 2e； 1 2 1 2 1 2 ②当e x  x 时， f(x)在(e，+)上单调递增，不符合题意； 1 2 考 ③当x ex 时，当x0时， f(e+x)=ef(e−x).令t =e+x(e,+)， f(t)=ef(2e−t)， 1 2 f(x ) f(x )=ef(2e−x )，又因为 f(x高) f(e)=0，所以 f(2e−x )0，因此 1 2 2 2 f(x ) f(x )=ef(2e−x ) f(2e−x ).因为x e，2e−x e，由 f(x)的单调性得，x +x 2e. 1 2 2 2 1 2 1 2 省 故C正确. D. 因为g(0)= f(0)+e2−20，g(2e)= f(2e)+e2 −20，g(e)= f(e)−2=−20，所以 东 0 x e x 2e. 1 2 先证x +x 2e.即广证2e−x x ，即g(2e−x )0，只需证 1 2 1 2 1 f(2e−x )+(2e−x −e)2 −20ef(x )+(e−x )2 −20. 1 1 1 1 事实上，ef(x )+(e− x )2 −2  f(x )+(e− x )2 −2 = g(x ) = 0，因此x +x 2e得证. 1 1 1 1 1 1 2 此时有0 x e x 2e−x 2e. 1 2 1 因为 f(x ) = −(x −e)2 +2 = −(2e− x −e)2 +2 −(x −e)2 +2= f(x )，又 f(x )0，所以 1 1 1 2 2 1 4f(x ) 1 2 . f(x ) 1 f(x ) 因为 f(x ) f(2e−x )=ef(x )，又 f(x )0，所以 2 e. 2 1 1 1 f(x ) 会 1 f(x ) 综上，1 2 e，D正确. 究 f(x ) 1 研 三、填空题 12. 考 【答案】29 13. 高 【答案】令𝑥 =1得(1+2)5 =243=𝑎 +𝑎 +𝑎 +𝑎 +𝑎 +𝑎 ， 5 4 3 2 1 0 令𝑥 =−1得(−1+2)5 =1=−𝑎 5 +省𝑎 4 −𝑎 3 +𝑎 2 −𝑎 1 +𝑎 0 ， 则𝑎 +𝑎 +𝑎 = (𝑎5+𝑎4+𝑎3+𝑎2+𝑎1+𝑎0 )−(−𝑎5+𝑎4−𝑎3+𝑎2−𝑎1+𝑎0) = 243−1 =121， 5 3 1 2 2 且𝑎 +𝑎 +𝑎 = (𝑎5+𝑎4+𝑎3+𝑎东 2+𝑎1+𝑎0 )+(−𝑎5+𝑎4−𝑎3+𝑎2−𝑎1+𝑎0) = 243+1 =122， 4 2 0 2 2 故𝑎5+𝑎3+𝑎1 = 121 . 𝑎4+𝑎2+𝑎0 122 广 14. 【答案】𝑦2 − 𝑥2 =1,(𝑦 ≠−3) 9 16 【解析】以𝐻𝐹所在直线为𝑥轴，𝐺𝐸所在直线为𝑦轴建立平面直角坐标系。 因为|𝐴𝐵|=8，|𝐵𝐶|=6，所以𝑂(0,0)，𝐻(−4,0)，𝐹(4,0)，𝐸(0,−3)，𝐺(0,3)，𝐶(4,3)，所以𝑂⃗⃗⃗⃗⃗𝐻⃗ =(−4,0)， 会 𝐶⃗⃗⃗⃗𝐹⃗ =(0,−3)，𝑂⃗⃗⃗⃗𝐶⃗ =(4,3)，又因为𝑂⃗⃗⃗⃗⃗𝑄⃗ =𝑘𝑂⃗⃗⃗⃗𝐻⃗⃗ ，𝐶⃗⃗⃗⃗𝑁⃗ =𝑘𝐶⃗⃗⃗⃗𝐹⃗ ，所以𝑂⃗⃗⃗⃗⃗𝑄⃗ =(−4𝑘,0)，𝐶⃗⃗⃗⃗𝑁⃗ =(0,−3𝑘)，所以 𝑄(−4𝑘,0)，𝑁(4,3−3𝑘)。 究 因为𝐸(0,−3)，𝑄(−4𝑘,0)，所以直线𝐸𝑄的方程为𝑦 =− 3 𝑥−3 ①，因为𝐺(0,3)，𝑁(4,3−3𝑘)，所以 研4𝑘 直线𝐺𝑁的方程为𝑦 =− 3𝑘 𝑥+3 ②。 4 考 由①可得𝑘 =− 3𝑥 (𝑥 ≠0)，代入②化简可得𝑦2 − 𝑥2 =1,(𝑥 ≠0)，结合图像易知点𝑅可到达𝐺(0,3)， 4(𝑦+3) 9 16 高 但不可到达𝐸(0,−3)所以点𝑅的轨迹方程为𝑦2 − 𝑥2 =1,(𝑦 ≠−3)。 9 16 省 四、解答题 东 15. 【解答】（1） cos2B−cos2A=2sin2C−2sinBsinC， 广  ( 1−2sin2 B ) − ( 1−2sin2 A ) = 2sin2C−2sinBsinC，------------------------------1分 即sin2 A=sin2 B+sin2C−sinBsinC.--------------------------------------------------2分 由正弦定理得a2 =c2 +b2 −bc，---------------------------------------------------------3分 1 由余弦定理得cosA= ，-------------------------------------------------------------------5分 2 5π A(0,π),A= ；----------------------------------------------------------------------6分 3 （2）设AB =c,AC =b， 1( ) 1 会 依题意可得AP = b+c ,BC =b−c,BQ = b−c-----------------------------------7分 2 2 究 1 2 2 19 1 2 2 所以| AP|= b +2bc+c = ，| BQ|= b −bc+c = 7 ----------------9分 2 2 4 研 1( )1  1 2 1 1 2 17 APBQ = b+c  b−c  = b − bc− c = − -----------------------------11 分 2 2  4 4 2 4 考 APBQ 17 133 所以cosPGQ = = − ----------------------------------------------13分 | AP|| BQ| 266 高 16. 省 ( ) 【解答】设点H的坐标为(x,y)，因为点A的坐标是 − 3,0 ，所以直线AH的斜率 东 y ( ) k = x− 3 ……………………1分 广 AH x+ 3 同理，直线BH 的斜率 y ( ) k = x 3 ………………………2分 BH x− 3 由已知，有 会 y y 1( )  =− x 3 …………………3分 x+ 3 x− 3 3 究 化简，得点H的轨迹方程为 研 x2 ( ) + y2 =1 x 3 …………………………4分 3 考 ( ) ( ) 点H的轨迹是除去 − 3,0 ， 3,0 两点的椭圆.………………………5分 高 （2）证明： 设E(x ,y )，F(x ,y ) 省 1 1 2 2 东 ①当直线l斜率不存在时，可知x = x ，y =−y ，且有 1 2 2 1 x2 广 1 + y2 =1   3 1  ……………………………………………7分 y −y 1 k k = 1  1 =−  AE AF x + 3 x + 3 3  1 1 联立可解得x =0，y =1，此时直线l为x=0…………………………8分 1 1 6②设直线l：y=kx+b，则此时有： y y (kx +b)(kx +b) k2x x +kb(x +x )+b2 1 k k = 1  2 = 1 2 = 1 2 1 2 =− ……………9分 AE AF x + 3 x + 3 x x + 3(x +x )+3 x x + 3(x会+x )+3 3 1 2 1 2 1 2 1 2 1 2 y =kx+b 究 联立直线方程与椭圆方程  x2 ，消去y可得： ( 3k2 +1 ) x2 +6kbx+3b2 −1=0……………10分 + y2 =1   3 研 −6kb 考3b2 −3 根据韦达定理可得：x +x = ， x x = ………………………………………………11分 1 2 3k2 +1 1 2 3k2 +1 高 代入斜率关系式并化简可得：b2 − 3kb=0，则b=0或b= 3k……………………………………12分 省 ( ) 当b= 3k时，则直线l：y =k x+ 3 恒过A点与题意不符，舍去………………………………13分 东 故b=0，直线l恒过原点(0,0)…………………………………………………………………………14分 广 结合①，②可知，直线l恒过原点(0,0)，原命题得证…………………………………………………15分 17. 【解答】 （1） 在底面ABCD中，因为AC是底面直径，所以ABC=ADC=90 ，又AB= AD，故 会 1 ACB ACD，所以BAC =DAC = BAD=30，BC =CD=4，AB= AD=4 3. 2 究 1 因为PC是圆柱的母线，所以PC ⊥面ABCD，所以V =( AC)2PC =16PC，--------- 2分 1 2 研 1 1 1 1 16 3 V = 2 ABBCPC = 2 4 34PC = PC，--------------------------- 4分 2 3 2 3 2 考 3 V 因此， 1 = 3. -------------------------------------------------------------------------------------------- 5分 V 高 2 （2） 省 以C为坐标原点，以CA，CP为x,z轴正方向，建立如图所示的空间直角坐标系. 东 广 7会 究 研 因为BAC=DAC=30,AB= AD，所以考ABE ADE，故AEB=AED=90 ，所以 1 BE = DE = AB=2 3,AE =6,CE = AC−AE =2，故PC=kCE=2k.----------------------------- 6分 高 2 因此C(0,0,0),A(8,0,0),D(2,2 3,0),P(0,0,2k),CD =(2,2 3,0),CP =(0,0,2k)， 省 PA=(8,0,−2k)，-------------------------------------------------------------------------------------------------------- 8分 东1 8 因为PA=kPF ，所以PF = PA=( ,0,−2)，则 k k 广 8 8 F( ,0,2k−2),CF =( ,0,2k−2). k k 设平面FCD和平面PCD的法向量分别为n=(x ,y ,z ),m=(x ,y ,z )，则有： 1 1 1 2 2 2  8 nCF = x +(2k−2)z =0  k 1 1  nCD=2x +2 3y =0  1 1 会  mCP=2kz =0  2 ------------------------------------------------ 9分  mCD=2x +2 3y =0 究 2 2 1 3 取n=( (k2 −k),− (k2 −k),1),m=(−3, 3,0). ----研------------------------------------------------ 13分 4 12 设平面FCD与平面PCD的夹角为，所以有： 考 |−k2 +k| 2 39 cos=|cosm,n|= = 1−sin2= ,解得：k =4. ------------ 15分 (k2 −k)2 +12高 13 18. 省 【解答】 （1）因为 f(x)的图像与g(x东)的图像关于直线x=−1对称，所以 f(−1−x)= g(−1+x).………1分 又因为 f(−1−x)=(−1−x)−1ln(−1−x)=(−2−x)ln(−1−x)，所以 广 g(−1+x)=(−2−x)ln(−1−x)，………………………………………………………………………2分 令t =−1+x，则x=t+1， 所以g(t)=−2−(t+1)ln−1−(t+1)=(−3−t)ln(−2−t)，……………………………………3分 因此g(x)=(−3−x)ln(−2−x). ………………………………………………………………………4分 （2）证明： 8解法1：当x1时，x−10且lnx0，此时 f(x)=(x−1)lnx0；…………………………6分 当0 x1时，x−10且lnx0；此时 f(x)=(x−1)lnx0， ……………………………8分 故综上 f(x)0. ………………………………………………………………………………………9分 1 会 解法2： f(x)=lnx+1− ，………………………………………………………………………5分 x 1 1 究 f(x)= + 0，…………………………………………………………………………………6分 x x2 因此当x1， f(x) f(1)=0；当0 x1时， f(x)研 f(1)=0；………………………7分 因此 f(x)在(0,1)上单调递减，在[1,+)上单调递增，…………………………………………8分 考 故 f(x) f(1)=0；………………………………………………………………………………9分 （3）证明：不妨取曲线y =ex 上的一点B(x ,ex 1)，设g(x)=lnx在A处的切线即是h(x)=ex 在B处的 高1 切线，………………………………………………………………………………………………11分 1 省1 1 1 则g(x )=h(x )  =ex 1，得x =ln ，则B的坐标为(ln , ). …………………12分 0 1 x 1 x x x 0 0 0 0 东x +1 由于(x −1)lnx = x +1，所以lnx = 0 ， ……………………………………………13分 0 0 0 0 x −1 0 广 1 1 lnx − lnx − 0 x 0 x 又因为k = 0 = 0 ， ………………………………………………………14分 AB 1 x +lnx x −ln 0 0 0 x 0 x +1 1 x2 +1 0 − 0 x −1 x x (x −1) 1 所以k = 0 0 = 0 0 = = g(x )，………………………会……………………16分 AB x +1 x2 +1 x 0 x + 0 0 0 0 x −1 x −1 0 0 究 综上，k =k =k ， …………………………………………………………………………17分 AB B切 A切 所以直线AB既是lnx的切线，也是ex的切线. 研 19. 考 【解答】（1） f(x)=(ex +1)dx=ex +x+C，其中C为常数. -------------------------------- 2分 高 而 f(0)=2，即1+0+C=2，所以C =1， 进而 f(x)=ex +x+1. ----------------省------------------------------------------------------------------------ 3分 y = x2 （2）联立 ，解得x =−3，x =2，------------------------------------------------------ 4分 东1 2 y =−x+6 当−3x2时，−x+6x2， 广 1 1 令g(x)=−x+6−x2 ，F(x)=g(x)dx=− x2 +6x− x3+C，------------------------------ 7分 2 3 5 8 9 149 则围成的面积S =2 g(x)dx =F(2)−F(−3）= (−2+16− )−(− −18+9)= .-------- 9分 −2 3 2 6 9（3）令F(x)=  f(x)dx， 由题意可知，a,b[0,+)，ab，满足F(a)−F(0)F(b)−F(0)， 即F(a)F(b)，即F(x)=  f(x)dx在[0,+)上单调递增，------------------------------------- 11分 会 进而 f(x)0在[0,+)恒成立，ex −1−2mx0在(0,+)恒成立. ----------------------------- 12分 究 ex −1 ex −1 （法一）由于x0，即 m，令g(x)= ，-------------------------------------------- 13分 研 2x 2x 2xex −2ex +2 g(x)= ，令h(x)=2xex −2ex +2 考，h(x)=2xex 0，所以h(x)在[0,+)上单调递增， 4x2 所以h(x)h(0)=0，即g(x)0，进而g(x)在[0,+)单调递增，------------------------- 15分 高 ex −1 ex 1 1 1 而 lim g(x)= lim = lim = ，所以g(x) ，所以m . ----------------------- 17分 x→0+ x→0+ 2x x→0+ 2 省 2 2 2 （法二）由于 f(0)=0，要使 f(x)=ex −1−2mx0，则 f(0)0，若不然，f(0)0，则存在0， 东 1 使得 f()0，矛盾. f(x)=ex −2m, f(0)0,即e0 −2m0，m ，--------------- 14分 2 1 广 1 下面证明m 是充分条件，当m 时， f(x)=ex −2m0,所以 f(x)在[0,+)单调递增，所以 2 2 1 f(x) f(0)=0.综上，m . ------------------------------------------------------------------------- 17分 2 会 究 研 考 高 省 东 广 10