广东省2025届高三数学一调模拟卷（试题）_8月_2408082025届广东省普通高中毕业班第一次调研考试_广东省高考研究会：广东省2025届高三数学一调模拟卷

秘密★启用前 试卷类型： A 2025 届广东省普通高中毕业班调研考试（一） 会 数 学 究 一、选择题：本题共 8 小题，每小题 5 分，共 40 分。在每小题给出的四个选项中，只有一项是符合题目 研 要求的。 考 1．已知集合A={xZ|x2 −8x+150}，B={x|x5}，则AB= 高 A. {3} B. {3,4} C. {4,5} D. {3,4,5} z 2. 已知z ，z 是两个虚数，则“z 省，z 均为纯虚数”是“ 1 为实数”的 1 2 1 2 z 2 A．充分不必要条件 东 B．必要不充分条件 C．充要条件 广 D．既不充分也不必要条件 3．已知a和b 的夹角为150°，且 a 2， b 3，则(a 2b) b A. 9 B. 3 C. 3 D. 9  2  4. 已知sin(+ )−sin= ，则cos(2+ )= 3 3 3 会 5 1 1 5 A. B. C. D. 9 9 9 究9 n 5．已知等比数列a 为递增数列，b = . 记S ，T 分研别为数列a ，b 的前n项和，若a =aa ， n n a n n n n 2 1 3 n S +T =12，则S = 考 3 3 n 1 1 A. 4n−1−1 B. ( 4n−1−1 ) C. ( 4n −1 ) D. 4n−2 4 高12 6．已知体积为4 3的球O与正四棱锥的底面和 4 个侧面均相切，已知正四棱锥的底面边长为4 3. 则 省 该正四棱锥体积值是 128 3 80 3 东 A. B. 43 3 C. 96 3 D. 3 3 7．斐波那契数列因数学广家斐波那契以兔子繁殖为例而引入，又称“兔子数列”.这一数列如下定义：设{a } n 为 斐 波 那 契 数 列 ， a =1 ， a =1 ， a =a +a (n3,nN*) ， 其 通 项 公 式 为 1 2 n n−1 n−2 1 1+ 5 1− 5 a = [( )n −( )n].设n是log [(1+ 5)x −(1− 5)x] x+4的正整数解，则n的最大 n 5 2 2 2 值为 数学试题 第1页（共4页）A.5 B.6 C.7 D.8 8．函数 f(x)=lnx与函数g(x) mx2 1有两个不同的交点，则m的取值范围是 1 1 1 1 A. ( , ) B. ( , ) C. (0, ) D. (0, ) e2 2e2 e2 会 2e2 二、选择题：本题共 3 小题，每题 6 分，共 18 分。在每小题给出究的选项中，有多项符合题目要求。全部 选对的得6分，部分选对的得部分分，有选错的得0分。 研 9．现有十个点的坐标为 (x ,0),(x ,0), ,(x ,0) ，它们分别与(y ,10), (y ,10), , (y ,10) 关于 1 2 10 1 2 10 点(3,5)对称. 已知x ,x , ,x 的平均数为a考，中位数为b，方差为c，极差为d ，则y ,y , ,y 1 2 10 1 2 10 这组数满足 高 A. 平均数为6−a B. 中位数为6−b 省 C. 方差为c D. 极差为d 东 10．设z，z，z 是非零复数，则下列选项正确的是 1 2 3 A．z 2 = z 2 广 1 1 B． z +z = z + z 1 2 1 2 C．若 z −2−2i =2，则 z +1−6i 的最小值为3 1 1 D．若 z +i + z −i =4，则 z 的最小值为 3 2 2 2 11．已知定义在R上的函数 f(x)的图象连续不间断，当x0，f(e+x)−ef(e−x)=0，且当x0时， 会 f(e+x)+ f '(e−x)0，则下列说法正确的是 A. f(e)=0 究 B. f(x)在(−,e)上单调递增，在(e，+)上单调递减 研 C. 若x  x ， f(x ) f(x )，则x +x 2e 1 2 1 2 1 2 f(x ) D. 若x ,x 是g(x)= f(x)+(x−e)2 −2在(0,考2e)内的两个零点，且x  x ，则1 2 e 1 2 1 2 f(x ) 1 高 三、填空题：本题共3题，每小题5分，共15分. {a } 省 12．已知等差数列 n 的首项a = 2，公差d =3，求第10项a 的值为 . 1 10 13．若(𝑥+2)5 =𝑎 𝑥5+𝑎 𝑥4+𝑎 𝑥3+𝑎 𝑥2+𝑎 𝑥+𝑎 ，则𝑎5+𝑎3+𝑎1 = . 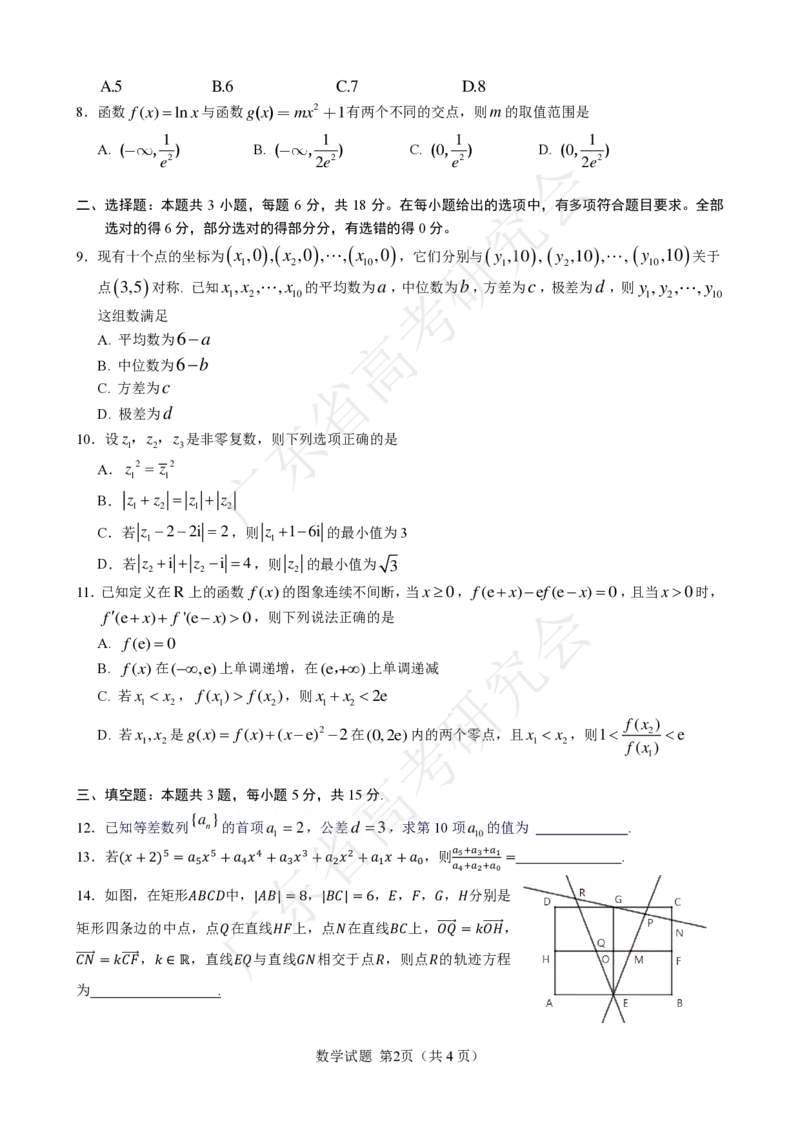5 4 东3 2 1 0 𝑎4+𝑎2+𝑎0 14．如图，在矩形𝐴𝐵𝐶𝐷中，|𝐴𝐵|=8，|𝐵𝐶|=6，𝐸，𝐹，𝐺，𝐻分别是 广 矩形四条边的中点，点𝑄在直线𝐻𝐹上，点𝑁在直线𝐵𝐶上，𝑂⃗⃗⃗⃗⃗𝑄⃗ =𝑘𝑂⃗⃗⃗⃗𝐻⃗⃗ ， 𝐶⃗⃗⃗⃗𝑁⃗ =𝑘𝐶⃗⃗⃗⃗𝐹⃗ ，𝑘 ∈ℝ，直线𝐸𝑄与直线𝐺𝑁相交于点𝑅，则点𝑅的轨迹方程 为 . 数学试题 第2页（共4页）四、解答题：本题共5小题，共77分。解答应写出文字说明、证明过程或演算步骤。 15．（13分） 在 ABC中，角A,B,C的对边分别为a,b,c,已知cos2B−cos2会A=2sin2C−2sinBsinC. （1）求 A; 究 （2）若b=2,c =3,P,Q分别为边a,b上的中点，G为 ABC的重心，求PGQ的余弦值. 研 16．（15分） 设 A，B两点的坐标分别为 ( − 3,0 ) ，考( 3,0 ) . 直线AH ，BH 相交于点H ，且它们的 1 斜率之积是− . 设点H的轨迹方程为高C. 3 （1）求C； 省 （2）不经过点A的直线l与曲线C相交于E、F 两点，且直线AE与直线AF 的斜率之积 1 东 是− ，求证：直线l恒过定点. 3 广 17．（15分） 如图所示，四边形ABCD是圆柱底面的内接四边形，AC是圆柱的底面直径，PC是圆柱的母线，E 是AC与BD的交点，AB= AD，BAD=60 ，AC =8. 会 究 研 考 V （1）记圆柱的体积为V ，四棱锥P−ABCD的体积为V ，求 1 ; 1 2 V 2 高 （2）设点F 在线段AP上，且存在一个正整数k，使得PA=kPF ，PC=kCE，若已知平面FCD 13 与平面PCD的夹角的正弦值为 省，求k的值. 13 东 18．（17分） 已知函数 f(x)=(x−1)lnx， 广 （1）已知函数 f(x)=(x−1)lnx的图像与函数g(x)的图像关于直线x=−1对称，试求g(x)； （2）证明 f(x)0； （3）设x 是 f(x)=x+1的根，则证明：曲线 y=lnx在点A(x ,lnx )处的切线也是曲线y =ex 的切 0 0 0 线. 数学试题 第3页（共4页）19．（17分） 如 果 函 数 F(x) 的 导 数 为 F(x)= f(x) ， 可 记 为  f(x)dx= F(x) ， 若 f(x)0 ， 则 b  f(x)dx= F(b)−F(a)表示曲线 y= f(x)，直线x=a，x=b以及x轴围成的“曲边梯形”的面积. 会 a 2 如：2xdx= x2 +C，其中C为常数； 2xdx=(22 +C)−(0+C)=4，则表示x=0，x=1，y=2x+C 0 究 及x轴围成图形面积为4. （1）若 f(x)=(ex +1)dx， f(0)=2，求 f(x)的表 研 达式； （2）求曲线y= x2 与直线y=−x+6所围成图 考 形的面积； （3）若 f(x)=ex −1−2mx， x[0,+)，其中mR，对a,b[0,+) ，若ab ，都满足 高 a b  f(x)dx f(x)dx，求m的取值范围. 0 0 省 东 广 会 究 研 考 高 省 东 广 数学试题 第4页（共4页）