文档内容
高三数学参考答案
令 ,解得 ,令k = 0,得 ,
1.D 解:将数据从小到大排列:2,3,5,7,9,10,16,18,20,23.∴ ,则
取第8个数,选D.
∴C正确.令 ,解得 ,∴ 在 上的唯一极值点为
2.C 解:由题意得 ,∴抛物线方程为 ,∴点 ,∴ ,故选C
3.B 解:对于A,若 则 或
,∴D正确,故选ACD
对于B,若 则
对于C,若 则 或 或 与 相交 10.BC 解: , ,
对于D,若 则 或l与n异面
∴ , ,∴B正确
4.C 解:令 , , ,由: ,得
∵M与N可能同时发生,∴M与N不互斥,∴A错误
∴ 是公比为2的等比数列, ,选C
∵ ,∴C正确
5.D 解:当AB过圆心O时, 最大为4,当 时, 最小为 ,
∵ ,∴D错误
∴ ,故选D
故选BC
6.A 解:∵ ,∴P在以AB为直径的圆上,设AB中点为C,
11.ACD 解:对于A,令 得 ,∴ ,故A正确
则P在P 处时原式取最小值, ,
1
∴选A 对于B,令 得 ,
令 , 得 ,∴ ,故B错
7.C 解:∵
误
∴ ,∴ ∴选C 对于C,令 , 得 ,∴
∴
8.A 解:过M作MB⊥x轴,由题意可得 . ,∴
,故C正确
设点 ,直线AM的斜率为k.
对于D,令 得 ,两边同时求导得 ,
则直线AM方程: 与双曲线 联立,
∴ ,∴ ,
故D正确
可得AM方程为 ,∴ , ,∴ .
12. 解:易知 , ,∴
9.ACD 解:∵ ,∴ ,∴A正确
13. 解:设A、C中点为O,O到平面DCE距离为A 到平面DCE距离的一半,设A 到平面
1 1 1
CDE的距离为d,由 ,即
令 ,则 ,∴ 的对称中心为 ,∴B错误
∴ ,∴O到平面CDE的距离为
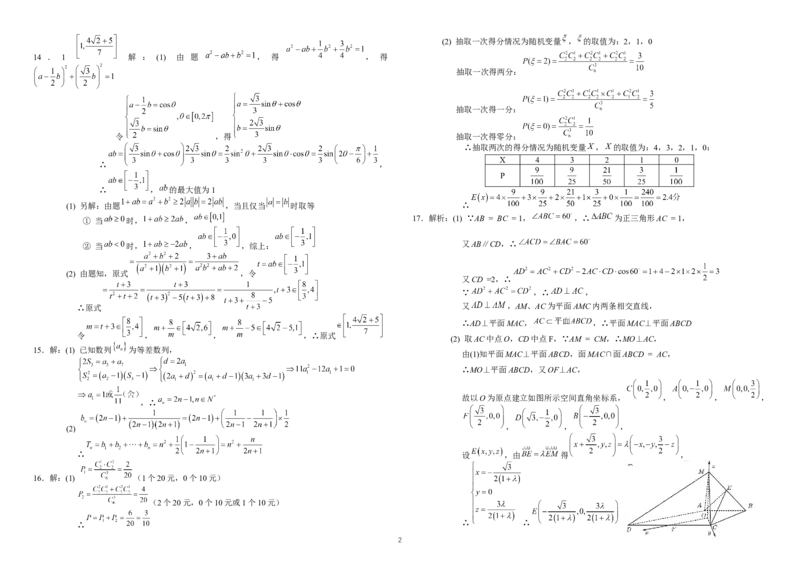
1(2) 抽取一次得分情况为随机变量 , 的取值为:2,1,0
14 . 1 解 : (1) 由 题 , 得 , 得
抽取一次得两分:
抽取一次得一分:
令 ,得 抽取一次得零分:
∴抽取两次的得分情况为随机变量 , 的取值为:4,3,2,1,0:
X 4 3 2 1 0
∴ ,
P
∴ , 的最大值为1
(1) 另解:由题 ,当且仅当 时取等 ∴
① 当 时, , 17.解析:(1) ∵AB = BC = 1, ,∴ 为正三角形AC = 1,
② 当 时, , ,综上: 又AB∥CD,∴
(2) 由题知,原式 ,令
又CD =2,∴
∵ ,∴ ,
∴原式 又 ,AM、AC为平面AMC内两条相交直线,
∴AD⊥平面MAC, ,∴平面MAC⊥平面ABCD
令 , , ,∴原式
(2) 取AC中点O,CD中点F,∵AM = CM,∴MO⊥AC,
15.解:(1) 已知数列 为等差数列,
由(1)知平面MAC⊥平面ABCD,面MAC∩面ABCD = AC,
∴MO⊥平面ABCD,又OF⊥AC,
故以O为原点建立如图所示空间直角坐标系, , , ,
,∴
(2) , , ,
∴ 设 ,由 得 ,
16.解:(1) (1个20元,0个10元)
(2个20元,0个10元或1个10元)
∴ ∴ ∴
2设平面ADM的法向量为
(3) 由第二问可知 ,∴
设直线CD的斜率为 ,直线CD方程为 ,设
则 取
设平面ACE的法向量为
联立 得
则 ∴
取 ,则 , ,
由 得: , ∴
∴ ,又 ,∴ 即
化简得 ,∴ ,由题意 ,∴ ,∴
18.解析:(1) 由题意知, ,∴ ,∴ ,又∵ 在椭圆上,∴ ,
19.解析:(1) 定义域为 ,
∴ ,∴椭圆 的标准方程为 ①当 即 时, , 在 上为增函数;
(2) 要证 即证 ,设
①当直线 斜率不存在时,由椭圆对称性可知 成立
②当 即 时, ,
②当直线 斜率存在时,设 ,则AB方程:
,
∴ 在 上为增函数,在 上为减函数
联立 得
(2) 时, ,
∴ ① 时, 在 上单调递减,∴
∴ 在 上单调递增,又 ,
联立 得
∴ ,使得 ,即 在 上有且仅有1个零点
② 时,由(1)知 在 上单调递减,
∴
即
∴ ,∴
∴
, ∴ ,
∴ 在 上没有零点
综上所述:
3③ 时, ,∴
即 在 上单调递减,又 ,
∴ 在 上有且仅有一个零点
综上所述, 在 上有且仅有两个不同的零点 和
(3) 令
由于 恒成立,且 ,同时 在 上连续,
∴ 是 的一个极大值点
∵ ,∴ 即 ,
下面证明 时 在 上恒成立
由(1)知 时, 在 上单调递增,在 上单调递减
∴ ,又 ,∴ 恒成立
4