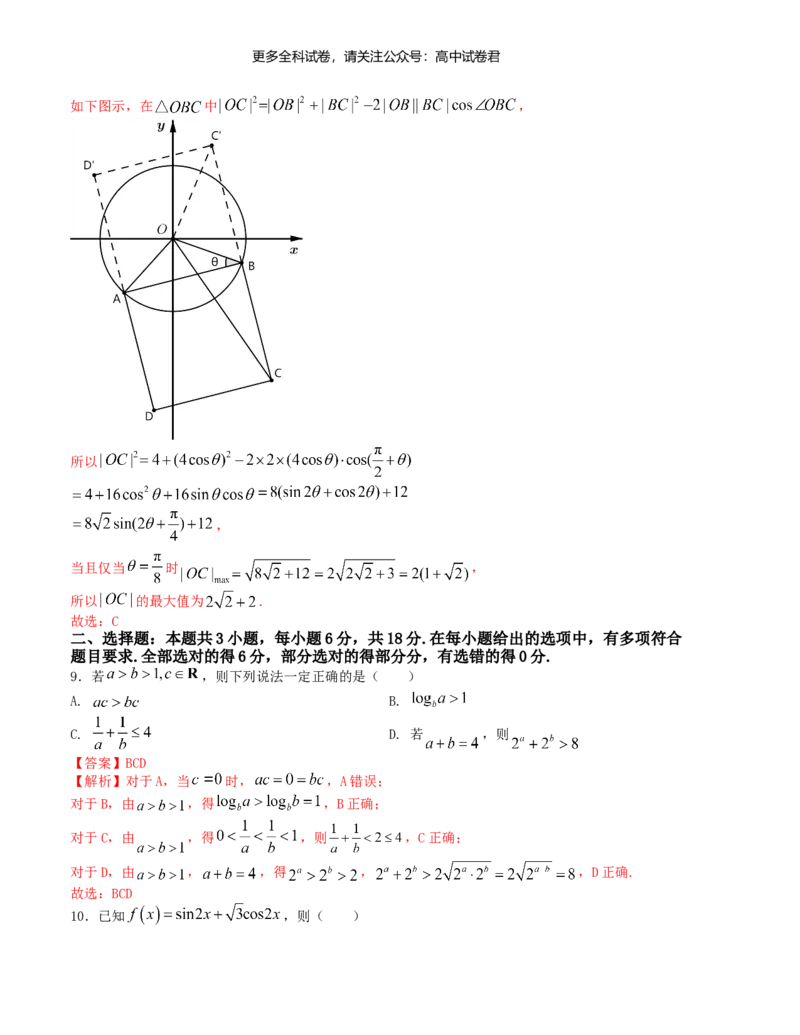
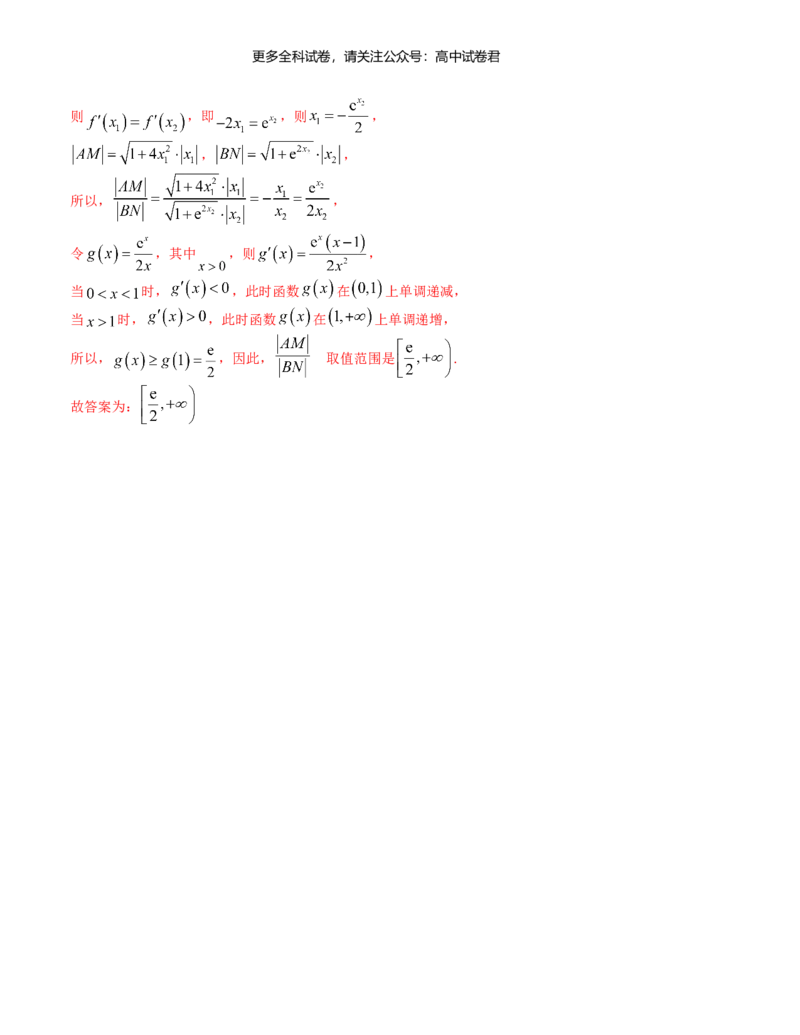文档内容
更多全科试卷,请关注公众号:高中试卷君
2024 届高三二轮复习“8+3+3”小题强化训练(14)
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有
一项是符合题目要求的.
1.在“美丽乡村”评选活动中,某乡镇 个村的得分如下: ,这组数据的中位
数和众数分别是( )
A. B. C. D.
【答案】D某乡镇 个村的得分: ,由小到大排序为: ,
所以中位数为 ,众数为 .
故选:D.
2.设等比数列 的各项均为正数,前 项和 ,若 , ,则 ( )
A. B. C. 15 D. 31
【答案】D
【解析】设等比数列 的公比为 , ,
当 时, , ,所以 .
所以 , ,
由于 且 ,所以 ,
则 ,所以 ,
所以 .
故选:D
3.若复数 满足 ,其共轭复数为 ,则下列说法正确的是( )
A. 对应的点在第一象限 B. 的虚部为
C. D.
【答案】C
【解析】由 两边乘以 得, ,
所以 对应点 在第四象限,
的虚部为 , , ,
所以C选项正确,ABD选项错误.
故选:C
4.椭圆 : ( )的左、右焦点分别为 , ,过 作垂直于 轴的直线
,交 于A, 两点,若 ,则 的离心率为( )
A. B. C. D.
【答案】A
【解析】因为 ,且直线 垂直于 轴,可知直线 : ,更多全科试卷,请关注公众号:高中试卷君
将 代入椭圆方程可得 ,解得 ,所以 ,
又因为 ,则 ,即 ,
可得 ,则 ,解得 .
故选:A.
5.如图1,儿童玩具纸风车的做法体现了数学的对称美,取一张正方形纸折出“十”字折痕,然后把
四个角向中心点翻折,再展开,把正方形纸两条对边分别向中线对折,把长方形短的一边沿折痕向外
侧翻折,然后把立起来的部分向下翻折压平,另一端折法相同,把右上角的角向上翻折,左下角的角
向下翻折,这样,纸风车的主体部分就完成了,如图2,是一个纸风车示意图,则( )
A. B.
C. D.
【答案】C
【解析】不妨设 ,则 ,
对于A项,显然 与 方向不一致,所以 ,故A项错误;
对于B项,由图知 是钝角,则 ,故B项错误;
对于C项,由题意知点 是线段 的中点,则易得: ,即得:
,故C项正确;
对于 D 项,由 ,而 与 显然不共线,故
.即 项错误.
故选:C.
6.已知函数 ,若 满足 ,则实数 的取
值范围是( )
A. B. C. D.
【答案】A
【解析】因为函数 定义域为 关于原点对称,
且 ,
所以 是定义在 上的偶函数,更多全科试卷,请关注公众号:高中试卷君
又 ,
当 时, ,则 ,所以 在 单调递增,
又 ,则 ,
且 ,则不等式 可化为
,即 ,
且 是定义在 上的偶函数, 在 单调递增,
则 ,即 ,即 ,
所以 ,即实数 的取值范围是 .
故选:A
7.在 中,角 所对的边分别为 , ,若 表示
的面积,则 的最大值为( )
A. B. C. D.
【答案】D
【解析】因为 ,
由正弦定理得 ,所以 ,
由余弦定理得 ,
所以 ,
令 ,则 ,当且仅当 ,即 时取等号,
所以 ,
故选:D.
8.在平面直角坐标系 中,已知圆 ,若正方形 的一边 为圆 的一条
弦,则 的最大值为( )
A. B. C. D. 5
【答案】C
【解析】令 且 , ,要使 最大有
,更多全科试卷,请关注公众号:高中试卷君
如下图示,在 中 ,
所以
,
当且仅当 时 ,
所以 的最大值为 .
故选:C
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合
题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.若 ,则下列说法一定正确的是( )
A. B.
C. D. 若 ,则
【答案】BCD
【解析】对于A,当 时, ,A错误;
对于B,由 ,得 ,B正确;
对于C,由 ,得 ,则 ,C正确;
对于D,由 , ,得 , ,D正确.
故选:BCD
10.已知 ,则( )更多全科试卷,请关注公众号:高中试卷君
A. 函数 的最小正周期为
B. 将函数 的图象向右平移 个单位,所得图象关于 轴对称
C. 函数 在区间 上单调递增
D. 若 ,则
【答案】AD
【解析】由 ,得 ,
对于 :最小正周期为 ,所以 正确;
对于 :将函数 的图象上所有点向右平移 ,
所得图象的函数解析式为 ,
而 为奇函数,所以其图象关于原点对称,所以 错误;
对于 :令 , ,化简得 ,
当 时, ,又因为 ,
所以函数在 单调递减,所以 错误;
对于 选项:因为 ,所以 ,
所以 ,所以 ,
即得 ,也就是 ,
所以 正确.
故选:AD.
11.在四棱锥 中, 是矩形, 为棱
上一点,则下列结论正确 是的( )
A. 点 到平面 的距离为更多全科试卷,请关注公众号:高中试卷君
B. 若 ,则过点 的平面 截此四棱锥所得截面的面积为
C. 四棱锥 外接球的表面积为
D. 直线 与平面 所成角的正切值的最大值为
【答案】ACD
【解析】如图,
对于A,因为 ,又 面 ,
所以 面 ,
所以点 到平面 的距离为 ,
又因为 ,
所以点 到平面 的距离为 ,故A正确;
对于B,因为 ,所以点 为棱 的中点,
取 中点 为,连接 ,可得平面 即平面 截此四棱锥所得截面,
且由于 是 的中点,点 为棱 的中点,
所以在 中, 是 的中位线,则 , ,
又因为四边形 是矩形,则 ,所以 ,
因 为面 ,
面 , 面 ,
所以四边形 是以 为下底、 为上底, 为高的直角梯形,
因为 ,在等腰三角形 中, ,且 平分 ,
则 ,
则平面 截此四棱锥所得截面的面积为 ,故B错误;
对于C,又因为 ,所以 ,
所以 ,即 ,其中 为 外接圆半径,
因为 面 ,更多全科试卷,请关注公众号:高中试卷君
所以四棱锥 外接球的半径为 ,
所以四棱锥 外接球的表面积为 ,故C正确;
对于D,因为 面 ,所以直线 与平面 所成角为 ,
所以当点 与点 重合时, 最大,积 ,故D正确.
故选:ACD.
三、填空题:本题共3小题,每小题5分,共15分.
12.某工厂由甲、乙两条生产线来生产口罩,产品经过质检后分为合格品和次品,已知甲生产线的次
品率为 ,乙生产线的次品率为 ,且甲生产线的产量是乙生产线产量的2倍.现在从该工厂生
产的口罩中任取一件,则取到合格品的概率为_____.
【答案】
【解析】由题意取到合格品的概率为 .
故答案为:0.95.
13.近期,哈尔滨这座“冰城”火了,2024年元旦假期三天接待游客300多万人次,神秘的鄂伦春族再
次走进世人的眼帘,这些英雄的后代讲述着英雄的故事,让哈尔滨大放异彩.现安排6名鄂伦春小伙
去三个不同的景点宣传鄂伦春族的民俗文化,每个景点至少安排1人,则不同的安排方法种数是
______.
【答案】540
【解析】若三个景点安排的人数之比为 ,则有 种安排方法;
若三个景点安排的人数之比为 ,则有 种安排方法;
若三个景点安排的人数之比为 ,则有 种安排方法,
故不同的安排方法种数是 .
故答案为:540
14.已知函数 ,若函数 的图象在点 和点
处的两条切线相互平行且分别交 轴于 、 两点,则 的取值范围为
______.
【答案】
【解析】当 时, , ,则 ,
当 时, , ,则 ,
因为函数 的图象在点 和点 处的两条切线相互平行,更多全科试卷,请关注公众号:高中试卷君
则 ,即 ,则 ,
, ,
所以, ,
令 ,其中 ,则 ,
当 时, ,此时函数 在 上单调递减,
当 时, ,此时函数 在 上单调递增,
所以, ,因此, 取值范围是 .
的
故答案为: