文档内容
专练 03(选择题-压轴)
1.已知 , , , ,则下列关系正确的
是( )
A. B. C. D.
【答案】C
【详解】
依题意, ,由于 ,函数 为减函数,故
.故选C.
2.(2020·全国高一月考)对于函数 ,给出下列选项其中正确的是( )
A.函数 的图象关于点 对称 B.函数 的最小正周期为
C.函数 在区间 上单调递增D.函数 有最大值,没有最小值
【答案】C
【分析】
由两角和的正弦公式化简 ,根据正弦型函数的图像与性质即可求解.
【详解】
由 ,当 时, ,所以 不是对称中心,A错误;
函数 的最小正周期为 ,所以B错误;
当 时, ,所以函数 在区间 上单调递增,故C正确;
, 函数 有最大值,有最小值,故D错误.
故选:C
【点睛】
本题主要考查了正弦型函数的单调性,周期,最值,对称中心,属于中档题.
3.设x,y,z为正数,且2x=3y=5z,则( )
A.2x<3y<5z B.5z<2x<3y C.3y<5z<2x D.3y<2x<5z
【答案】D
【详解】
令2x=3y=5z=m,分别可求得2x= = ,3y= = ,5z= = ,分别对
分母乘以30可得,30log =log 215,30log =log 310,30log =log 56,
m m m m m m
故而可得 ⇒log
m
310>log
m
215>log
m
56⇒3y<2x<5z.4.已知函数 ,如果方程 有三个不相等的实数解 ,则
的取值范围是( )
A. B. C. D.
【答案】D
【分析】
作出函数 的图像,转化为 与 有三个交点,求出 的范围以及 的关系,不妨设
,将 转化为关于 的函数,即可求出结论.
【详解】
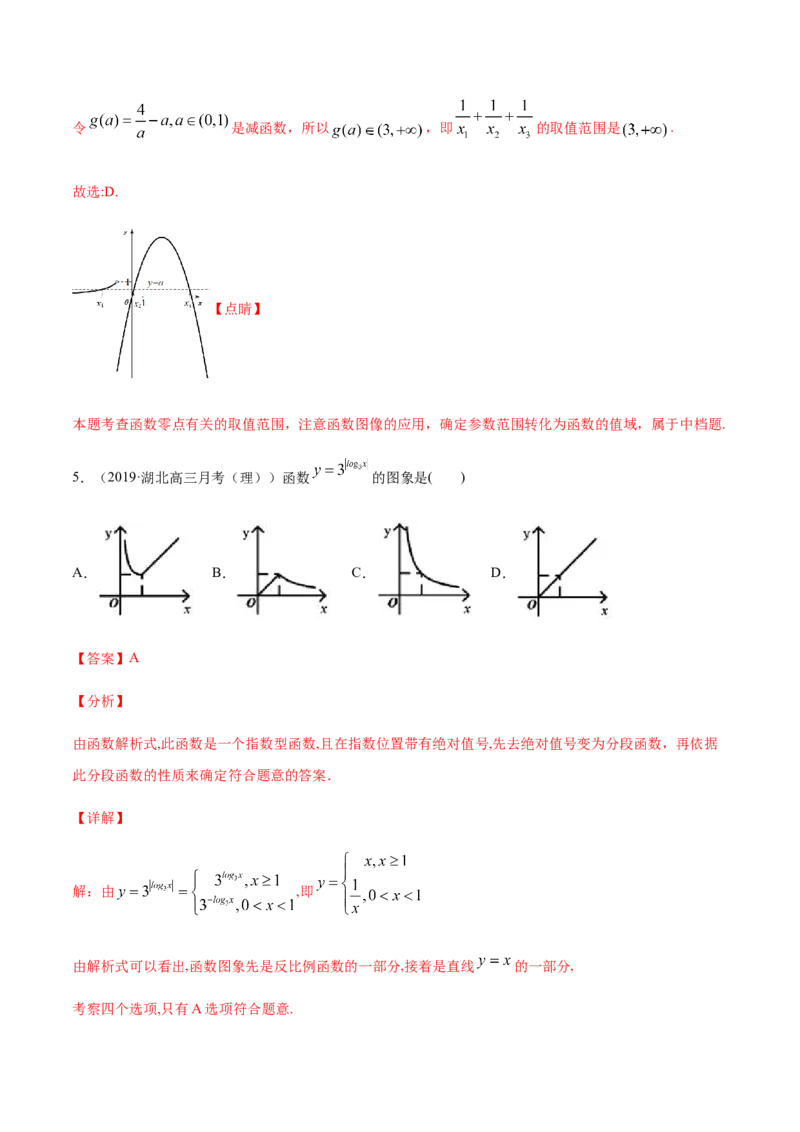
作出函数 图像,如下图所示:
方程 有三个不相等的实数解 ,
不妨设 , 与 有三个交点,所以 时,且
,
,令 是减函数,所以 ,即 的取值范围是 .
故选:D.
【点睛】
本题考查函数零点有关的取值范围,注意函数图像的应用,确定参数范围转化为函数的值域,属于中档题.
5.(2019·湖北高三月考(理))函数 的图象是( )
A. B. C. D.
【答案】A
【分析】
由函数解析式,此函数是一个指数型函数,且在指数位置带有绝对值号,先去绝对值号变为分段函数,再依据
此分段函数的性质来确定符合题意的答案.
【详解】
解:由 ,即
由解析式可以看出,函数图象先是反比例函数的一部分,接着是直线 的一部分,
考察四个选项,只有A选项符合题意.故选:A.
【点睛】
本题的考点是分段函数,考查分段函数的图象,作为函数的重要性质之一的图象问题也是高考常考点,而
指对函数的图象一直是考纲要求掌握并理解的,属于一般难度的题.
6.(2020·黑山县黑山中学高二月考)已知函数 在定义域 上是减函数,且
,则实数 的取值范围是( )
A. B. C. D.
【答案】B
【分析】
利用函数的单调性和定义域得出不等关系组,即得解.
【详解】
已知函数 在定义域 上是减函数,且 ,
故选:B
【点睛】
本题考查了利用函数的单调性解不等式,考查了学生转化划归,数学运算能力,属于基础题.
7.(2020·江苏宝应中学高三开学考试)已知定义在 上的奇函数 满足:当 时, ,若不等式 对任意实数 恒成立,则实数 的取值范围是( )
A. B.
C. D.
【答案】A
【分析】
求得函数 在 上的解析式,进而可判断出函数 在 上单调递增,由
,可得出不等式 对任意的实数 恒成立,可得出关于实数 的
不等式组,由此可解得实数 的取值范围.
【详解】
由于函数 为 上的奇函数,则 .
当 时, ,则 .
所以,对任意的 , ,则函数 为 上的增函数.
由 可得 ,即 ,
由题意可知,不等式 对任意的实数 恒成立.
①当 时,则有 ,在 不恒成立;
②当 时,则 .综上所述,实数 的取值范围是 .
故选:A.
【点睛】
本题考查利用函数的单调性求解函数不等式恒成立问题,考查计算能力,属于中等题.
8.已知函数 ,对任意的 , 恒成立,则x的取值范围为(
)
A. B. C. D.
【答案】A
【分析】
先根据函数的解析式判断出函数的单调性和奇偶性,即可将不等式 变形得到关于
的不等式 ,构造函数 ,即可列出不等式组解出 的取值范围.
【详解】
因为函数 , ,易知函数 为 上单调递增的奇函数,所以
,即 对任意的 恒成立,设
,只需 即可.
解不等式组 ,解得 .故选:A.
【点睛】
本题主要考查函数的奇偶性和单调性的综合应用,以及更换主元法的应用,意在考查学生的转化能力,属
于中档题.
9.(2019·山东寿光现代中学高二月考)正数 满足 ,则 的取值范围是( )
A. B. C. D.
【答案】A
【分析】
根据均值不等值,把已知条件转化成关于 的不等式,解不等式即可
【详解】
解:因为 是正数,所以 ,
即 ,当 ,即 时取等号,所以 ,
即 ,解得: (舍去)或 ,
所以 ,即 的取值范围是 .
故选:A.
【点睛】
本题考查均值不等式及解一元二次不等式,要注意均值不等式的条件(一正、二定、三相等).
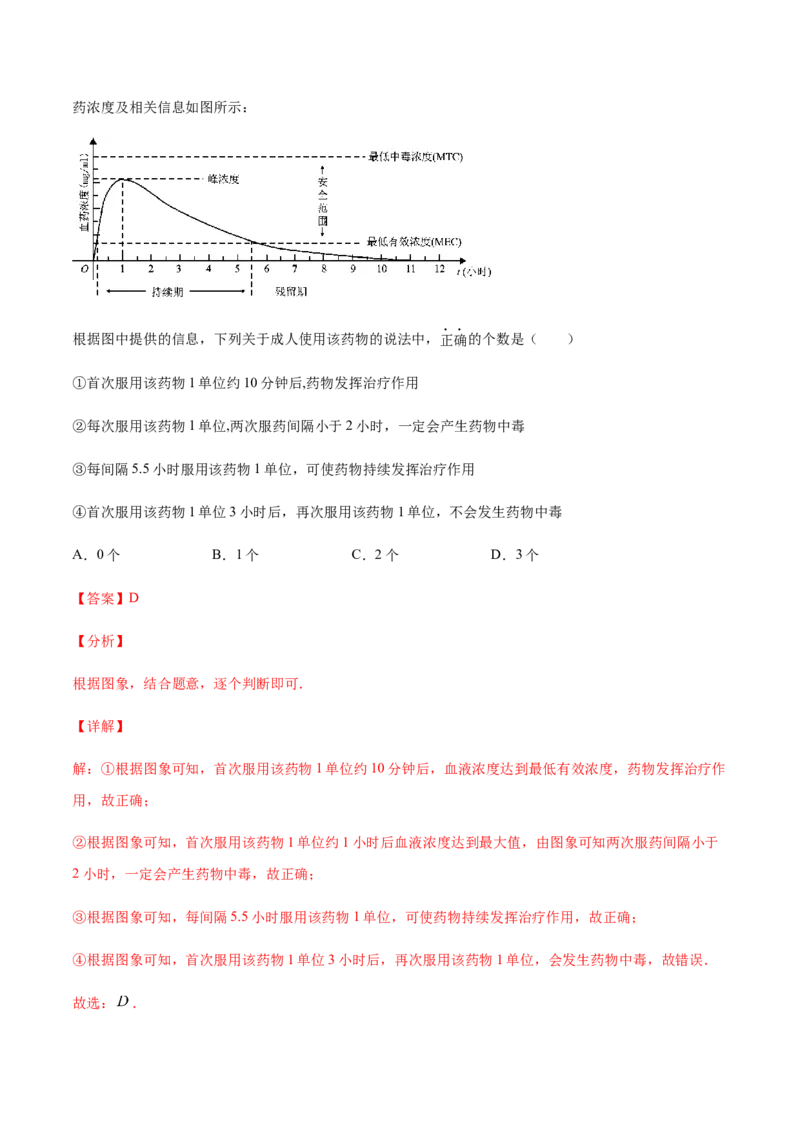
10.血药浓度(Plasma Concentration)是指药物吸收后在血浆内的总浓度,药物在人体内发挥治疗作用时,
该药物的血药浓度应介于最低有效浓度和最低中毒浓度之间,已知成人单次服用1单位某药物后,体内血药浓度及相关信息如图所示:
根据图中提供的信息,下列关于成人使用该药物的说法中,正确的个数是( )
①首次服用该药物1单位约10分钟后,药物发挥治疗作用
②每次服用该药物1单位,两次服药间隔小于2小时,一定会产生药物中毒
③每间隔5.5小时服用该药物1单位,可使药物持续发挥治疗作用
④首次服用该药物1单位3小时后,再次服用该药物1单位,不会发生药物中毒
A.0个 B.1个 C.2个 D.3个
【答案】D
【分析】
根据图象,结合题意,逐个判断即可.
【详解】
解:①根据图象可知,首次服用该药物1单位约10分钟后,血液浓度达到最低有效浓度,药物发挥治疗作
用,故正确;
②根据图象可知,首次服用该药物1单位约1小时后血液浓度达到最大值,由图象可知两次服药间隔小于
2小时,一定会产生药物中毒,故正确;
③根据图象可知,每间隔5.5小时服用该药物1单位,可使药物持续发挥治疗作用,故正确;
④根据图象可知,首次服用该药物1单位3小时后,再次服用该药物1单位,会发生药物中毒,故错误.
故选: .【点睛】
本题考查了函数图象的性质和对新定义函数的理解.难点是充分理解题意,根据图象解决实际问题.
11.已知函数 ,则 ( )
A. B. C.1 D.
【答案】D
【分析】
令 ,则 ,易证 为奇函数,由 求出
,再利用奇函数的性质即可求得 .
【详解】
令 ,则 ,
由 知函数 为奇函数,
因为 ,所以 ,
所以 .
故选:D
【点睛】
本题考查函数奇偶性的应用,对数换底公式的推论,属于中档题.
12.(2020·黑龙江大庆实验中学高一开学考试)在 上定义运算 , 时,不等式 有解,则实数 的取值范围是( )
A. B. C. D.
【答案】A
【分析】
转化条件得 在 上有解,利用基本不等式求得 在 的最大值即可得解.
【详解】
由题意可得 在 上有解,
所以 即 在 上有解,
又 ,当且仅当 时,等号成立,
所以 在 的最大值为 ,所以实数 的取值范围是 .
故选:A.
【点睛】
本题考查了基本不等式的应用及有解问题的解决,考查了运算求解能力与转化化归思想,属于中档题.
13.(2020·全国高三月考(文))已知二次不等式 的解集为,则 的最小值为( ).
A. B. C. D.
【答案】C
【分析】
由一元二次不等式的性质可得 , ,由基本不等式得出 的范围,将 表示为关于
的二次函数即可得解.
【详解】
∵二次不等式 的解集为 ,
∴ ,即 , ,∴ ,当且 时,等号成立,
∴ ,
∴当 时, 最小,最小值为 ,
故选:C.
【点睛】
关键点点睛:
(1)由一元二次不等式解的特征得出 ;
(2)由基本不等式得出 的范围;(3)将所求结果表示为关于 的二次函数.
14.(2020·重庆南开中学高三月考(理))已知函数 ,则不等式
的解集为( )
A. B. C. D.
【答案】D
【分析】
设 ,结合导数和二次函数的性质可判断两函数的单调性,由单调性的性质从而
可求出 的单调性;由奇偶性的定义判断出函数的奇偶性,从而可得 ,进而可选出正确答
案.
【详解】
解:设 ,由 ,当 时, ,
当 时, ,则 在 上单调递减,在 上单调递增,
由二次函数的性质可知, 在 上单调递减,在 上单调递增,
所以 在 上单调递减,在 上单调递增,
又 ,所以 为偶函数.由 可知,
,即 ,解得 ,
故选:D.【点睛】
本题考查了函数单调性的求解,考查了函数奇偶性的判断,考查了转化的思想,属于中档题.
15.(2020·上海格致中学高一月考)已知关于x的不等式组 仅有一个整数解,
则k的取值范围为( )
A. B. C. D.
【答案】B
【分析】
求出第一个不等式的解,讨论 的范围得出第二个不等式的解,根据不等式组只含有一个整数得出第二个
不等式解的端点的范围,从而得出 的范围.
【详解】
解:解不等式 得 或 ,
解方程 得 , .
(1)若 即 时,不等式 的解集是 ,
若不等式组只有1个整数解,则 ,解得: ,
(2)若 即 时,不等式 的解集是 , ,若不等式组只有1个整数解,则 ,解得: ,
3) (4
综上, 的取值范围是 , , ,
故选:B.
【点睛】
本题考查了一元二次不等式的解法,分类讨论思想,借助数轴可方便得出区间端点的范围,属于中档题.
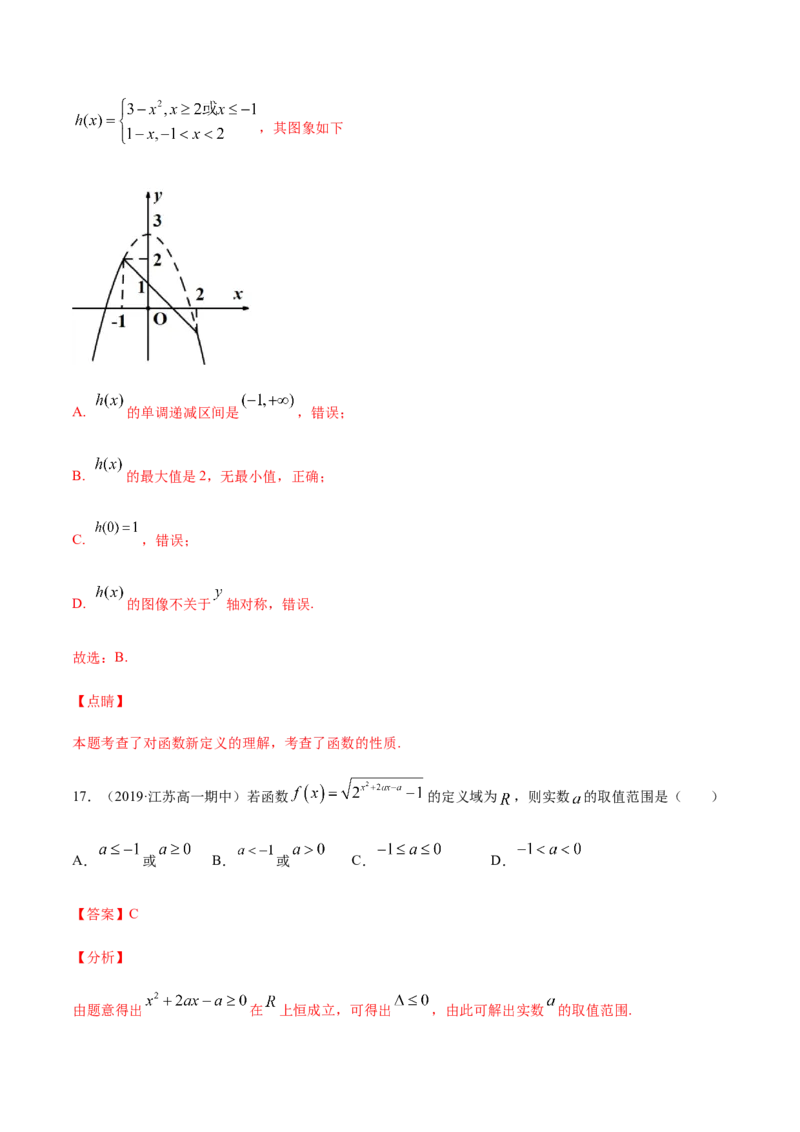
16.(2020·湖北荆州中学高一月考)对于任意的实数 表示 中较小的那个数,即
已知函数 设 ,下列说法
正确的是( )
A. 的单调递减区间是 B. 的最大值是2,无最小值
C. D. 的图像关于 轴对称
【答案】B
【分析】
首先弄清楚 的含义,换成 相当于分段函数,再根据函数的性质可逐项
判断排除.
【详解】
由题意得 ,即,其图象如下
A. 的单调递减区间是 ,错误;
B. 的最大值是2,无最小值,正确;
C. ,错误;
D. 的图像不关于 轴对称,错误.
故选:B.
【点睛】
本题考查了对函数新定义的理解,考查了函数的性质.
17.(2019·江苏高一期中)若函数 的定义域为 ,则实数 的取值范围是( )
A. 或 B. 或 C. D.
【答案】C
【分析】
由题意得出 在 上恒成立,可得出 ,由此可解出实数 的取值范围.【详解】
函数 的定义域为 , ,得 恒成立,
得 恒成立,即判别式 ,则 ,得 ,
故选:C.
【点睛】
本题考查利用函数的定义域求参数,同时也涉及了指数不等式以及二次不等式恒成立问题,考查运算求解
能力,属于中等题.
18.(2020·全国高一单元测试)已知函数 的定义域是 ,且满足 ,
,如果对于 ,都有 ,那么不等式 的解集为( )
A. B. C. D.
【答案】B
【分析】
计算得到 ,不等式化简为 ,根据函数定义域和单调性解得答案.
【详解】
令 ,得 ,即 ;
令 , ,得 ,即 ;
令 ,得 .由 ,可得 ,
又因为函数 的定义域是 ,且对于 ,都有 ,函数单调递减.
所以 ,即 ,解得 ,
即不等式 的解集为 .
故选:
【点睛】
本题考查了利用函数单调性解不等式,意在考查学生对于函数性质的综合应用.
19.(2019·河北新乐市第一中学高三月考)函数 的图象大致是( )
A. B. C. D.
【答案】C
【分析】
先判断函数为偶函数,再分段讨论函数值的情况,即可判断.
【详解】
解:函数的定义域为 ,
因为 ,所以 为偶函数,所以 的图像关于 轴对称,
当 时, 所以 ,
当 时, 所以 ,当 时,
故选:C
【点睛】
此题考查了函数图像的识别,关键是掌握函数的奇偶性和函数值的变化趋势,属于中档题.
20.奇函数 在 上为增函数,且 ,则不等式 的解集为( )
A. B. C. D.
【答案】C
【分析】
首先利用奇函数定义与 得出 与 同号,然后由奇函数定义求出 (1)
,最后结合 的单调性解出答案.
【详解】
由奇函数 可知 ,即 与 同号,
而 (1) ,则 (1) ,不合题意,又 在 上为增函数,则奇函数 在 上也为增函数,
当 时, (1) ,得 ,不满足;
当 时, (1) ,得 ,满足,
当 时, ,得 ,不满足;
当 时, ,得 ,满足;
所以 的取值范围是 .
故选: .
【点睛】
本题综合考查奇函数定义与利用单调性解不等式,考查了分类讨论思想的应用,属于中档题.
21.函数 的值域是( )
A. B. C. D.
【答案】A
【分析】
利用换元法,将根式转化 ,原函数即可转化成关于t的二次函数,注意t的取值范围,可求解
值域.【详解】
令 ,且 ,则 ,函数转化为
由 ,则 ,即值域为
故选:A.
【点睛】
函数解析式中含有根式的,可令根式等于t,进行换元,转化成关于t的二次函数,利用二次函数的性质可
求值域.
22.若函数 是定义在 上的减函数,又 是锐角三角形的两个内角,则( )
A. B.
C. D.
【答案】D
【分析】
依题意只需判断各选项中自变量的大小,由已知可得 ,根据正弦函数的单调性,得出
的大小关系,即可求解.
【详解】
是锐角三角形的两个内角, ,在 为增函数, ,
又函数 是定义在 上的减函数, .
故选:D.
【点睛】
本题考查抽象函数的函数值大小关系,利用函数的单调性,以及判断锐角三角形中角的三角函数大小是解
题的关键,属于中档题.
23.设函数 ,则满足 的 的取值范围是( )
A. B. C. D.
【答案】D
【分析】
根据 得到 ,讨论 的范围解得答案.
【详解】
函数 , 得到
当 时: 解得 ,即
当 时: 解得 ,即综上所述:
故答案选D
【点睛】
本题考查了分段函数的计算,分类讨论是一个常用的方法.
24.(2020·福建省南安市侨光中学高一月考)已知函数 , 若对任
意 ,总存在 ,使得 成立,则实数 的取值范围是( )
A. B. C. D.
【答案】A
【分析】
问题转化为 ,求出 在 上的最小值,而 为 或 ,解不等式
组 ,即可求解.
【详解】
,当 时最小值为-1
对任意 ,总存在 ,使得 成立,
只需 ,即 ,
而 为 或 ,只需 ,解得 .
故选:A
【点睛】
本题考查不等式存在成立和恒成立问题,转化为函数的最值是解题的关键,属于中档题.
25.(2020·内江市市中区天立学校高一月考)已知函数 ,若对任意 、 、 ,总
有 、 、 为某一个三角形的边长,则实数 的取值范围是( )
A. B. C. D.
【答案】C
【分析】
根据 ,分 和 两种情况求得函数的值域,然后再由
对任意 、 、 ,总有 、 、 为某一个三角形的边长,转化为
,对任意 、 、 恒成立求解.
【详解】
因为 、 、 为某一个三角形的边长,
所以 ,对任意 、 、 恒成立,函数
当 时, 在R上递减,函数的值域为 ,
所以 且 ,所以 ,又 ,所以 ;
当 时, 在R上递增,函数的值域为 ,
所以 且 ,所以 ,解得 ,所以 ;
综上 的取值范围是 ,故选:C
【点睛】
本题主要考查函数的值域的求法以及不等式恒成立问题,还考查了分析求解问题的能力,属于中档题.
26.(2020·湖北高三月考)若 ,设函数 的零点为 的零点
为 ,则 的取值范围是( )
A. B. C. D.
【答案】B
【分析】
把函数零点转化为两个函数图象交点的横坐标,根据指数函数与对数函数互为反函数,得到两个函数图象
之间的关系求出 , 之间的关系,根据两者之和是定值,利用基本不等式得到要求的结果.【详解】
函数 的零点是函数 与函数 图象交点 的横坐标,
函数 的零点是函数 与函数 图象交点 的横坐标,
由于指数函数与对数函数互为反函数,
其图象关于直线 对称,直线 与直线 垂直,
故直线 与直线 的交点 即是 , 的中点,
, ,
当 等号成立,而 ,故 ,故所求的取值范围是 , .
故选:B.
【点睛】
本题考查函数零点、反函数的性质、基本不等式求最值,考查函数与方程思想、转化与化归思想、数形结
合思想,考查逻辑推理能力和运算求解能力,求解时注意验证等号成立的条件.
27.若一系列函数的解析式和值域相同,但其定义域不同,则称这些函数为“同族函数”,例如函数
, 与函数 , 即为“同族函数”.下面函数解析式中也能够被用来构造
“同族函数”的是( )
A. B. C. D.
【答案】B【分析】
由题意,能够被用来构造“同族函数”的函数必须满足在其定义域上不单调,由此判断各个函数在其定义
域上的单调性即可.
【详解】
对A: 在定义域 上单调递增,不能构造“同族函数”,故A选项不正确;
对B: 在 递增,在 递减,在 递减,在 递增,能构造“同族函
数”,故B选项正确;
对C: 在定义域上递增,不能构造“同族函数”,故C选项不正确;
对D: 在定义域上递减,不能构造“同族函数”,故D选项不正确.
故选:B.
【点睛】
本题给出“同族函数”的定义,要求我们判断几个函数能否被用来构造“同族函数”,考查基本初等函数
的单调性的知识点,属于基础题.
28.设 ,若 是 的最小值,则实数a的取值范围为( )
A. B. C. D.
【答案】C
【分析】
利用二次函数的性质,先求出当 时的函数最值,然后结合一元二次函数的性质进行讨论即可.
【详解】解:当 时, ,
此时函数的最小值为 ,
若 ,则 ,此时 不是 的最小值,此时不满足条件,
若 ,则要使 是 的最小值,则满足 ,即 ,
解得 , ,
故选:C.
【点睛】
本题主要考查函数最值的求解,根据不等式的基本性质以及一元二次函数的性质是解决本题的关键.
29.设正实数 满足 ,则当 取得最大值时, 的最大值为( )
A. B. C. D.
【答案】C
【解析】
当且仅当 时成立,因此
所以
【考点定位】本题考查基本不等式的应用,考查运算求解能力、推理论证能力和转化思想、函数和方程思
想. 基本不等式的使用价值在于简化最值确定过程,而能否使用基本不等式的关键是 中的是否为定值,本题通过 得以实现.
30.秦九韶是我国南宋时期的数学家,他的成就代表了中世纪世界数学发展的主流与最高水平.他在著作
《数书九章》中叙述了已知三角形的三条边长 ,求三角形面积的方法.其求法是:“以小斜幂并大斜
幂减中斜幂,余半之,自乘于上,以小斜幂乘大斜幂减上,余四约之,为实.一为从隅,开平方得积.”若把
以上这段文字写成公式,即为 .已知三角形 的三条边长为 ,
其面积为12,且 ,则 周长的最小值为( )
A.12 B.14 C.16 D.18
【答案】C
【分析】
根据题意利用面积公式求出 的值,再将三角形 的周长用 表示,利用不等式放缩,可得出三角形周长
的最小值.
【详解】
解:由已知 ,可得 ,
两边平方解得 ,
又 ,可得 ,三角形 周长 ,
取等条件 ,周长的最小值为16,
故选C.
【点睛】
本题考查了利用秦九韶三角形面积公式解三角形的问题,以及不等式在最值中的应用,属于中档题.