文档内容
专练 07 解答题-基础
1.已知集合 ,集合 .
(1)当 时,求 ; (2)若 ,求实数 的取值范围.
【答案】(1) (2)
【分析】
(1)当 时, ,根据并集定义,即可求得 ;
(2)因为 ,分别讨论 和 两种情况,即可求得实数 的取值范围.
【详解】
(1)当 时,
又 ,则
(2)因为 ,
当 时, ,解得
当 时, ,解得
综上所述,实数 的取值范围为 .
【点睛】本题考查了并集运算和子集运算.本题的解题关键是掌握当 时,分别讨论 和 两种情况,考
查了分析能力和计算能力,属于基础题.
2.化简求值:
(1) ;(2) .
【答案】(1) ;(2) .
【分析】
根据指数幂的运算法则,以及根式与指数幂的互化公式,直接计算,即可得出结果.
【详解】
(1)
;
(2) .
【点睛】
本题主要考查指数幂以及根式的化简求值,属于基础题型.
3.已知 为第二象限角,且 .
(Ⅰ)求 与 的值; (Ⅱ) 与 的值.【答案】(Ⅰ) ;(Ⅱ) .
【分析】
(Ⅰ)根据同角的三角函数关系即可求出 与 的值;
(Ⅱ)利用齐次式弦化切与二倍角公式求值.
【详解】
解:(Ⅰ)∵ ,∴ , ,
又 ,且 为第二象限角,∴ ;
(Ⅱ) ,
.
【点睛】
本题主要考查同角的三角函数关系,属于基础题.
4.已知 , , , 为实数,求证: .
【答案】证明见详解
【分析】
由作差法,将两式作差整理,得到 ,即可证明结论成立.
【详解】
因为 , , , 为实数,
显然成立;
所以 .
【点睛】
本题主要考查不等式的证明,根据作差法证明即可,属于基础题型.
5.已知函数 .
(1)判断函数 的奇偶性,并证明;
(2)证明函数 在R上单调递增;
(3)若 ,求实数 的取值范围.
【答案】(1)函数 是奇函数;证明见解析;(2)证明见解析;(3) .
【分析】
(1)利用函数的奇偶性定义即可判断.
(2)利用函数的单调性定义以及证明函数单调性的步骤:“任取、作差、变形、定号”即可证明.
(3)利用奇偶性将不等式转化为 ,再利用单调性可得 ,解不等式即可求解.
【详解】
(1)函数 的定义域是 ,
因为 ,
即 ,所以函数 是奇函数.
(2)证明:任取 ,且 ,则
, 在R上单调递增.
(3)由(1)(2)知函数 是奇函数,所以 .
又函数 是 上的增函数,所以 ,解得 .
故实数 的取值范围是 .
【点睛】
本题考查函数奇偶性、单调性的证明,考查根据奇偶性、单调性求解,考查了学生对概念的理解和运用能
力,属于基础题.
6.已知函数 .(1)求函数 的单调区间; (2)求函数 取得最大值时的 集合.
【答案】(1) , (2)
【分析】
(1)由条件利用正弦函数的单调性,求得函数的单调区间.
(2)利用正弦函数的定义域和值域,求得函数取得最大值,以及此时的自变量 的值.
【详解】
(1) 在 上的增区间满足: , ,
∴ ,解得: , ,
所以单调递增区间为 , ,
单调递增区间为 , .
(2) ,
令: , ,解得: , ,
函数 取得最大值的 集合为: .
【点睛】本题主要考查正弦函数的单调性、正弦函数的定义域和值域,属于基础题.
7.在平面直角坐标系 中,锐角 的顶点在坐标原点 ,始边与 轴非负半轴重合,终边与单位圆交
于点 ,且点 的纵坐标为 .
(1)求 和 ; (2)求 的值.
【答案】(1) (2)
【分析】
(1)根据三角函数的定义求 ,再根据同角的平方关系求 ;
(2)由同角的商关系求出 ,再用二倍角公式的正切公式求 .
【详解】
解:(1)由题意可知, ,
∵角 为锐角,∴ ;
(2)由(1)知 ,则 .
【点睛】
本题主要考查三角函数的定义,考查同角的三角函数关系,考查二倍角的正切公式,属于基础题.8.已知对数函数 过点 .
(1)求函数 的解析式,并写出函数 的定义域;
(2)若 ,求 的取值范围.
【答案】(1) ,定义域为 ;(2)
【分析】
(1)设 ,代入点 计算即可;
(2)利用对数函数的单调性及定义域列不等式组求解即可.
【详解】
解:(1)设 ,
,所以 ,定义域为 ;
(2)由已知得 ,所以 的取值范围是 .
【点睛】
本题考查待定系数法求对数函数的解析式,考查对数函数单调性的应用,是基础题.
9.(1)已知f =x2+ ,求f(x);
(2)已知一次函数f(x)满足f(f(x))=4x-1,求f(x);【答案】(1)f(x)=x2+2;(2) 或 .
【分析】
(1)利用配凑法可求函数的解析式.
(2)利用待定系数法可求函数的解析式.
【详解】
(1)(配凑法)∵ ,
∴ .
(2)(待定系数法)∵f(x)是一次函数,∴设f(x)=ax+b(a≠0),
则f(f(x))=f(ax+b)=a(ax+b)+b=a2x+ab+b.
∵f(f(x))=4x-1,∴ ,解得 或 , .
【点睛】
本题考查函数的解析式的求法,常用的方法有待定系数法、配凑法、函数方程组法等,注意根据题设的特
征选择合适的方法,本题属于基础题.
10.已知 , 是方程 的两个根,且 ,求m的值.
【答案】
【分析】由根与系数关系,先得到 , ,再由对数运算,即可求出结果.
【详解】
由题意可得, , , ,即 ;
又 ,所以 ,因此 ,满足 ,
故 .
【点睛】
本题主要考查对数的运算,熟记对数运算法则即可,属于基础题型.
11.已知函数 ,且 ,求 的值.
【答案】
【分析】
根据 ,对 分类讨论先求出 的值,再代入求出 .
【详解】
解:当 时, , ,舍去,
当 时, , ,符合题意,
.【点睛】
本题主要考查分段函数的函数值的求法,属于基础题.
12.(1)已知 ,求 的最小值;(2)求 的最大值.
【答案】(1) ;(2) .
【解析】
【分析】
(1)将代数式变形为 ,然后利用基本不等式可求出所求代数式的最小值;
(2)根据代数式有意义得出 ,分 或 、 两种情况讨论,利用基本不等式
可求出所求代数式在 时的最大值,综合可得出结论.
【详解】
(1) , , ,
当且仅当 时,即当 时等号成立, 的最小值为 ;
(2)由 知 .
当 或 时, ;
当 时, ,由基本不等式可得 .当且仅当 ,即当 时等号成立.
综上, 的最大值为 .
【点睛】
本题考查利用基本不等式求最值,在应用基本不等式时,要注意“一正二定三相等”三个条件的成立,考
查计算能力,属于基础题.
13.若不等式 的解集是 ,
(1)求 的值; (2)求不等式 的解集.
【答案】(1) ;(2) .
【分析】
(1)根据不等式的解集可得对应的一元二次方程的两根,由韦达定理可解得结果;
(2)代入 的值,解一元二次不等式可得结果.
【详解】
(1)依题意可得: =0的两个实数根为 和2,
由韦达定理得: ,解得: ;.
(2)则不等式 ,可化为 .
所以 ,所以 ,所以 ,
故不等式 的解集 ..
【点睛】
本题考查了一元二次不等式的解法,属于基础题.
14.已知函数 且点 在函数 的图象上.
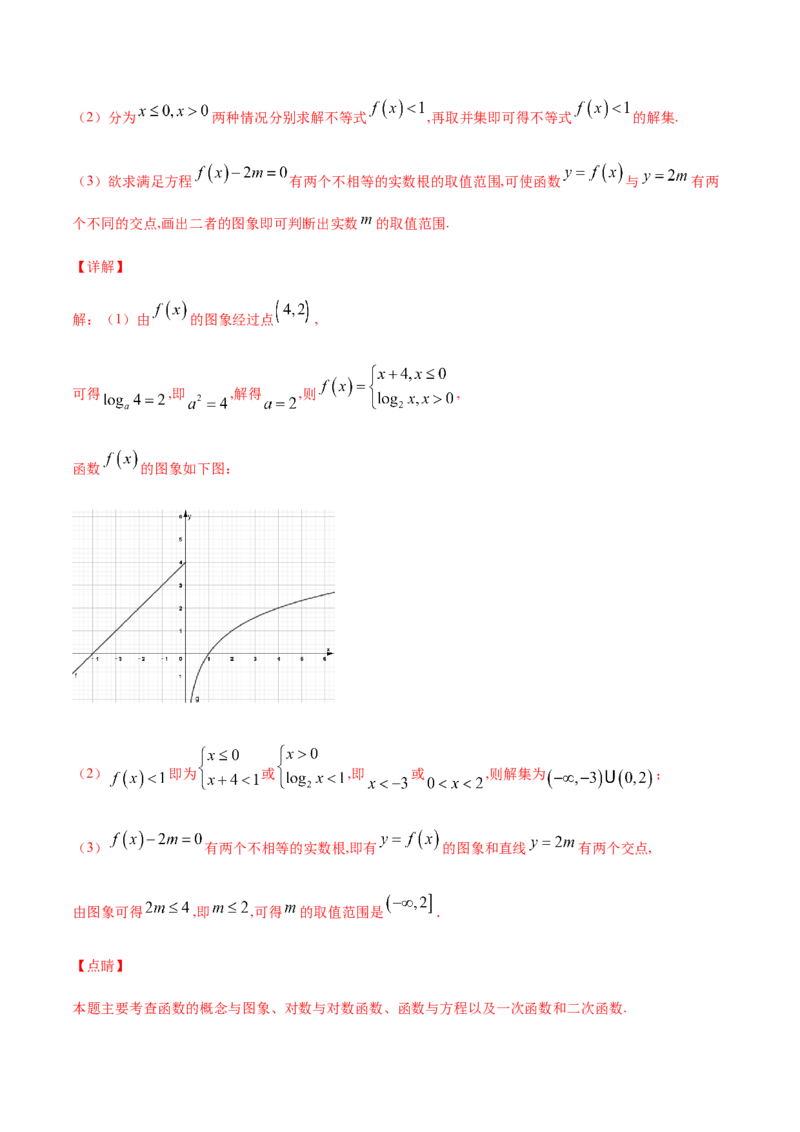
(1)求函数 的解析式,并在图中的直角坐标系中画出函数 的图象;
(2)求不等式 的解集;
(3)若方程 有两个不相等的实数根,求实数 的取值范围.
【答案】(1) ,图像见解析(2) (3)
【分析】
(1)将点 代入 中,即可求解的值,进而求得函数 的解析式,画出函数f(x)的图
象.(2)分为 两种情况分别求解不等式 ,再取并集即可得不等式 的解集.
(3)欲求满足方程 有两个不相等的实数根的取值范围,可使函数 与 有两
个不同的交点,画出二者的图象即可判断出实数 的取值范围.
【详解】
解:(1)由 的图象经过点 ,
可得 ,即 ,解得 ,则 ,
函数 的图象如下图:
(2) 即为 或 ,即 或 ,则解集为 ;
(3) 有两个不相等的实数根,即有 的图象和直线 有两个交点,
由图象可得 ,即 ,可得 的取值范围是 .
【点睛】
本题主要考查函数的概念与图象、对数与对数函数、函数与方程以及一次函数和二次函数.15.如图是函数 的图像,求 、 、 的值,并确定其函数解
析式.
【答案】 , , , .
【分析】
本题首先可以根据周期 计算出 ,然后根据最大值为 以及最小值为 得出 ,最后将点
代入函数中即可求出 并得出函数解析式.
【详解】
因为周期 ,所以 , ,
因为最大值为 ,最小值为 ,所以 , ,
将点 代入 中,得 ,解得 ,
因为 ,所以 , .【点睛】
本题考查根据三角函数图像求函数解析式,可根据函数的周期、最值以及点的坐标来求解,考查数形结合
思想,考查计算能力,是简单题.
16.已知函数 , .
(1)求函数 的单调递增区间;(2)求 时,函数 的值域.
【答案】(1) ;(2)
【分析】
(1)先根据降幂公式以及辅助角公式化简三角函数,令 即可得出答
案;
(2)由 得 ,由此即可求出答案.
【详解】
解: ;
(1)令 ,得 ,
所以函数 的单调递增区间为 ;(2)由 得 ,∴ ,
从而函数 的值域为 .
【点睛】
本题主要考查三角函数的化简以及性质,属于基础题.
17.我市某商场销售小饰品,已知小饰品的进价是每件3元,且日均销售量 件与销售单价 元可以用
这一函数模型近似刻画.当销售单价为4元时,日均销售量为400件,当销售单价为
8元时,日均销售量为240件.试求出该小饰品的日均销售利润的最大值及此时的销售单价.
【答案】当该小饰品销售单价定位8.5元时,日均销售利润的最大,为1210元.
【分析】
根据已知条件,求出 ,利润 ,转化为求二次函数的最大值,即可求解.
【详解】
解:由题意,得 解得
所以日均销售量 件与销售单价 元的函数关系为 .
日均销售利润
.当 ,即 时, .
所以当该小饰品销售单价定位8.5元时,日均销售利润的最大,为1210元.
【点睛】
本题考查函数实际应用问题,确定函数解析式是关键,考查二次函数的最值,属于基础题
18.一个扇形的所在的圆的半径为5,该扇形的弧长为5
(1)求该扇形的面积; (2)求该扇形中心角的弧度数.
【答案】(1) ;(2)1.
【分析】
(1)根据扇形面积公式直接计算;(2)根据扇形弧度数公式 计算求值.
【详解】
解:(1) , , ;
(2)
【点睛】
本题考查弧度制,扇形面积,重点考查基本公式,属于基础题型.
19.化简下列各式:
(1) ;(2)已知 ,且 ,求 的值.
【答案】(1) ;(2)
【分析】
(1)利用指数的运算性质即可求解.
(2) ,且 ,可得 ,将原式因式分解、通分、化简即可求解.
【详解】
(1)
(2)由 ,且 ,可得 ,
20.已知函数 .
(1)求函数 周期及其单调递增区间;
(2)当 时,求 的最大值和最小值.【答案】(1)最小正周期为 ,单调递增区间为 ;(2)最大值为 ,最
小值为 .
【分析】
(1)首先根据三角恒等变换可得 ,根据周期公式即可求出周期;然后再令
,即可求出函数的单调递增区间;
(2)由题意可知 ,进而 ,由此即可求出函数的最值.
【详解】
因为
所以 ;
所以 的最小正周期为 ;
令 ,所以
所以 的单调递增区间为 ;(2) ,所以
所以 ,所以 的最大值为 ,最小值为 ;
【点睛】
本题主要考查了三角恒等变换和正弦函数的相关性质,属于基础题.