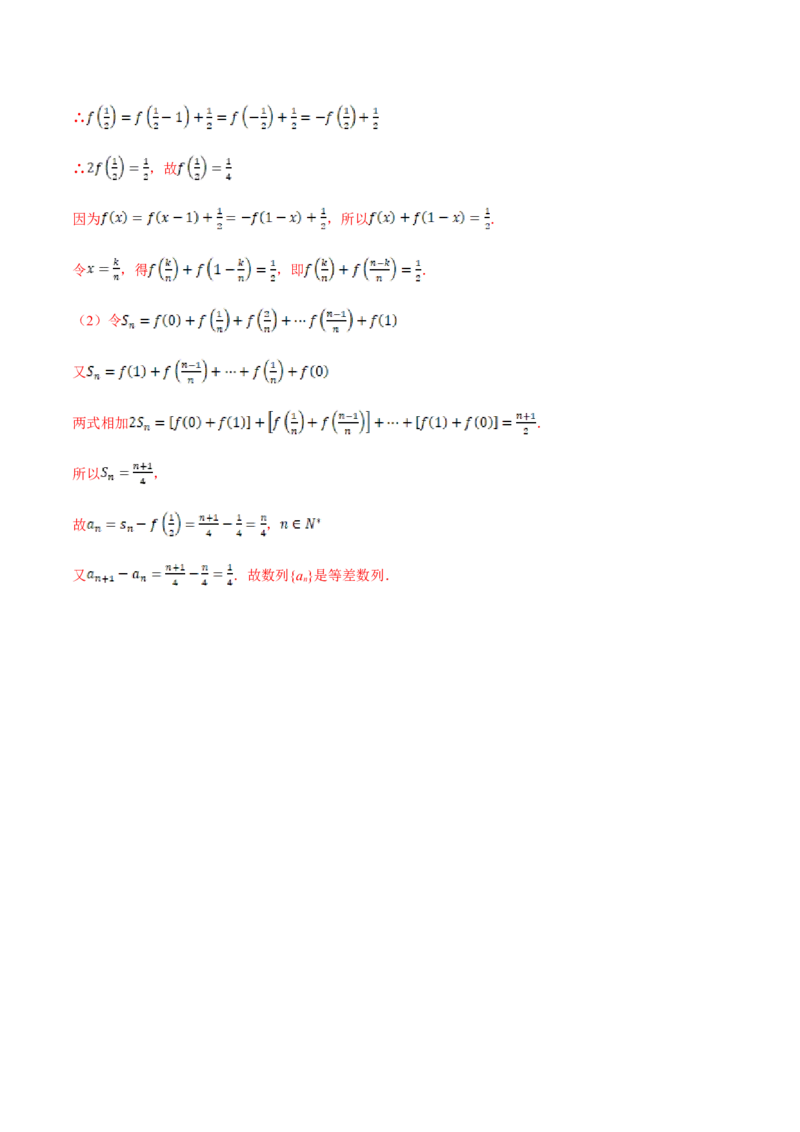专题19数列的求和（解析版）_E015高中全科试卷_数学试题_选修2_01.同步练习_同步练习（第四套）_高中数学新教材人教A版选择性必修配套提升训练(等10份资料)

专题19 数列的求和 一、单选题 1 a  1．（2019·商丘市第一高级中学高二期中（理））数列{a }的前n项和为S ，若 n nn1 ，则S  n n 9 （ ） 1 9 1 A．1 B．10 C．10 D．30 【答案】C 【解析】 1 1 1 1 1 1 1 1 1 9 a    n nn1 n n1, S 9  1  2  2  3 ... 9  10  10 . 故选：C S nn12n222 22n12n1 2．（2018·甘肃省武威十八中高二课时练习）化简 n 的 结果是（ ） 2n12n2 2n1n2 2n n2 2n1n2 A． B． C． D． 【答案】D 【解析】 ∵S=n+（n﹣1）×2+（n﹣2）×22+…+2×2n﹣2+2n﹣1 ① n 2S=n×2+（n﹣1）×22+（n﹣2）×23+…+2×2n﹣1+2n ② n ∴①﹣②式得；﹣S=n﹣（2+22+23+…+2n）=n+2﹣2n+1 n ∴S=n+（n﹣1）×2+（n﹣2）×22+…+2×2n﹣2+2n﹣1n+2﹣2n+1=2n+1﹣n﹣2 n 故答案为：D 1 1 1 1 1 1 ,3 ,5 ,7 , ,(2n1) ,   3．（2020·江西省江西师大附中高三月考（理））数列 2 4 8 16 2n 的前n项和 S n的值等于（ ）1 1 1 1 n2 1 2n2 n1 n2 1 n2 n1 A． 2n B． 2n C． 2n1 D． 2n 【答案】A 【解析】 1 1 1 S (13 2n1)(    ) n  2 4  2n 1 1 (1 ) (12n1)n 2 2n   2 1 1 2 1 n2 1 2n , 故选：A {a } a 9 a 15  (1)na  4．（2019·福建省莆田一中高三期中（文））等差数列 n 中， 4 ， 7 ，则数列 n 的前 20项和等于（ ） A．-10 B．-20 C．10 D．20 【答案】D 【解析】 a a 3d 1596 d 2, a 3 7 4 ，解得 1 ，所以 20 a a a a a ...a a 10d 20 n 1 2 3 4 19 20 ，故选D． i1 4 a  5．（2020·珠海市第二中学高一开学考试）已知数列{a }且满足： n1 2a ，且a 4，则S 为数列 n n 1 n {a } n S = n 的前 项和，则 2020 （ ） A．2019 B．2021 C．2022 D．2023 【答案】D 【解析】4 a  由 n1 2a ，a 4， n 1 4 4 4 a  2 a  1 a  4 所以 2 2a ， 3 2a ， 4 2a ， 1 2 3 {a } 3 S a a a 3 所以数列 n 是以 为周期的数列， 3 1 2 3 ， S =673S a 673342023 所以 2020 3 1 . 故选：D a  n S S 7,S 63 6．（2018·厦门市华侨中学高二期中）已知等比数列 n 的前 项和为 n，若 3 6 ，则数列 na  n n 的前 项和为（ ） 3(n1)2n 3(n1)2n A． B． 1(n1)2n 1(n1)2n C． D． 【答案】D 【解析】 a  1q3 1 7 1q { 当 时，不成立，当 时， a  1q6 ，两式相除得 1q3 1 7 ，解得： 1 63   q 1 q 1 1q 1q6 1q3 63 q= 2 a 1 a aqn1 2n1 na n2n1 ， 1 即 n 1 ， n ， s 122322 ......n2n1 n ， 2s  12222 ......n12n1n2n s 1222 ......2n1n2n n ，两式相减得到： n12n  12 n2n 1n2n 1 ，所以s n 1n12n ，故选D. 7．（2019·福建省厦门第六中学高二期中（理））已知数列 满足 ，则数列 的最小值是 A．25 B．26 C．27 D．28 【答案】B 【解析】 因为数列 中， ，所以 ， ， ， ，上式相加，可得 ，所以 ，所以 ，当且仅当 ，即 时，等式相等，故选B． 2 f x 8．（2020·江苏省高二期中）设函数 2x 1，利用课本中推导等差数列前n项和的方法，求得 f 5 f 4 f 0 f 4 f 5 的值为（ ） 9 11 A．9 B．11 C．2 D． 2 【答案】B 【解析】 2 2 2 22x 2  f x f x     f x ， 2x 1 2x 1 2x 1 2x 2x 1  2x 1 2 22x 2  12x    2 ， 2x 1 12x 2x 1 S  f 5 f 4 f 0 f 4 f 5 设 ，S  f 5 f 4  f 0  f 4 f 5   则 ， 2S 11f 5 f 5 11222 两式相加得   ，因此，S 11. 故选：B. 二、多选题 a  2(n1)a na 0  nN* 9．（2020·海南省高三其他）已知数列 n 的首项为4，且满足 n n1 ，则（ ） a   n A． n 为等差数列 a  B． n 为递增数列 a  n S (n1)2n14 C． n 的前 项和 n  a  n2 n  n  T  D．2n1的前n项和 n 2 【答案】BD 【解析】 a a a  a n1 2 n  n 1 a 4 由2(n1)a na 0得n1 n ，所以 n 是以 1 1 为首项，2为公比的 n n1 a n 42n1 2n1 a n2n1 等比数列，故A错误；因为 n ，所以 n ，显然递增，故B正确； S 122 223 n2n1 2S 123224  n2n2 因为 n  ， n  ，所以 22 12n  n2n2 S 122 23 2n1n2n2 ，故S (n1)2n2 4， n  12 n a n2n1  a  n(1n) n2 n n  n  n  T   故C错误；因为2n1 2n1 ，所以2n1的前n项和 n 2 2 ， 故D正确.故选：BD 10．已知数列{a}为等差数列，首项为1，公差为2，数列{b}为等比数列，首项为1，公比为2，设 n n c a n b n，T 为数列{c }的前n项和，则当T＜2019时，n的取值可以是下面选项中的（ ） n n n A．8 B．9 C．10 D．11 【答案】AB 【解析】 b 2n1 由题意，a＝1+2（n﹣1）＝2n﹣1， n ， n c a  n b n 2•2n﹣1﹣1＝2n﹣1，则数列{c }为递增数列， n 其前n项和T＝（21﹣1）+（22﹣1）+（23﹣1）+…+（2n﹣1） n 2  12n  n ＝（21+22+…+2n）﹣n 2n+1﹣2﹣n． 12 当n＝9时，T＝1013＜2019； n 当n＝10时，T＝2036＞2019． n ∴n的取值可以是8，9． 故选：AB a a  n  nN* 11．（2020·山东省高二期末）已知数列 a  满足a 1， n1 23a ，则下列结论正确的有 n 1 n （ ）  1   3 A． a 为等比数列   n 1 B． a n  的通项公式为 a n  2n13 a  C． n 为递增数列  1    D．  a  的前 n 项和 T 2n2 3n4 n n 【答案】ABD【解析】 1 23a 2 1 1 1  n  3 32( 3) 340 因为a a a ，所以a a ，又a ， n1 n n n1 n 1  1  1 所以   a n 3  是以4为首项，2位公比的等比数列， a n 342n1 即a n  2n 1 13 ，a n 为递减数列，  1     a n  的前 n 项和 T n (22 3)(233)  (2n13)2(2122   2n)3n 2(12n) 2 3n2n2 3n4 12 . 故选：ABD a  S 12．（2019·江苏省苏州实验中学高二月考）已知等差数列 n 的首项为1，公差d 4，前n项和为 n， 则下列结论成立的有( ) S   n A．数列 n 的前10项和为100 a , a , a m21 B．若 1 3 m成等比数列，则 n 1 6   C．若 aa 25，则n的最小值为6 i1 i i1 1 16 25  a a a a D．若 ，则m n 的最小值为12 m n 2 10 【答案】AB 【解析】 a 4n3 S 2n2 n 由已知可得: n , n , S S  10119 n =2n1  n =100 n ,则数列 n 为等差数列,则前10项和为 2 .所以A正确; a , a , a a2=a a , a 81 a =4m381 m21 1 3 m成等比数列,则 3 1 m m ,即 m ,解得 故B正确;1 1 1 1  n 1 1 1 1 1 1 1  n 6 =   = 1      =       因为aa 44n3 4n1所以 aa 4 5 5 9 4n3 4n1 4n1 25,解 i i1 i1 i i1 n6 n mn12 得 ,故 的最小值为7,故选项C错误;等差的性质可知 ,所以 1 16 1  1 16 1  n 16m  1 25 n 16m  =    mn  1  16   1724 = m n 12m n  12 m n  12 12 ,当且仅当m n 时,即 48 48 n=4m n=4m 5 时取等号,因为m,nN*,所以 5 不成立,故选项D错误. 故选:AB. 三、填空题 {a } S a 3，S 10 13．（2020·宁夏回族自治区银川一中高三三模（理））等差数列 n 的前n项和为 n， 3 4 ， n 1   则 S _____. k1 k 2n 【答案】n1 【解析】 nn1 S  a a 2d 3，S 4a 6d 10，故a d 1，故 n 2 ， 3 1 4 1 1 n 1 n 2 n 1 1   1  2n   2  2 1      S kk1 k k1  n1 n1. k1 k k1 k1 2n 故答案为：n1. a  a 1 a 2n a a  n 14．（2020·全国高三月考（文））已知数列 n 满足： 1 ， n1 n，则数列 n 的前 项和S  n __________. 2n1n2 【答案】 【解析】 a a 2n n2 由已知， n1 n ，当 时， 12n a a a a a a a a 1222 2n1  2n 1 n 1 2 1 3 2 n n1 12 ， a 1 a 2n 1 又 1 满足上式，所以 n ， 2  12n S 222 2n n n2n1n2 n 12 . 2n1n2 故答案为： a  a 1 a a 2n nN* S a  15．（2020·安徽省高三一模（理））已知数列 n 中， 1 ， n n1 ，记 n为 n 的前n S 项和，则 2n=____________. 32n 3 【答案】 【解析】 a a a 2n1 n1 n2  n2  2 因为a 1，aa 2，所以 a 2 .又 a a a 2n ， 1 1 2 2 n n1 n a  a a 所以数列 n 的奇数项是以 1为首项，2为公比的等比数列，偶数项是以 2为首项，2为公比的等比数列. 1  12n 2  12n S   32n 3 故 2n 12 12 . 32n 3 故答案为： . 1 a 1 16．（2020·山东省临沂第一中学高二期中）已知数列 a  满足a 2， n1 a ，设 a  的前n项 n 1 n nS a  S  和为 n，则 6 __________， 2017 __________． 【答案】1 1010 【解析】 1 1 1 a 1 a 1  由a 2， n1 a ，有 2 a 2 1 n 1 1 1 a 1 1,a 1 2 3 a 4 a ，………… 2 3 a  则数列 n 是以3为周期的数列. 3 a a a  又 1 2 3 2 ，201736721 3 S 672 a 1010 所以 a 6 a 3 1 ， 2017 2 1 故答案为：(1). 1 (2). 1010 四、解答题 9x  1   2  4022 f x f    f    f   17．（2019·全国高一课时练习）设函数 9x 3 ，计算 4023 4023 4023. 【答案】2011 【解析】 9x 91x 9x 9 9x 3 f(x) f(1x)      1 解：由已知 9x 3 91x 3 9x 3 939x 9x 3 39x ，  f(x) f(1x)1 ，  1   2  4022 S  f  f  f       设 4023 4023 4023 4022 4021  1  S  f  f  f       4023 4023 4023  1  4022   2  4021  4022  1  2S  f  f  f  f  f  f                 4023 4023  4023 4023  4023 4023 2S 4022， S 2011，  1   2  4022 f  f  f 2011       即 4023 4023 4023 18．（2020·福建省高三其他（文））已知数列 a n  为递减的等差数列， a 1， a 6为方程 x2 9x140 的 两根． a  （1）求 n 的通项公式； b a 2n b  （2）设 n n ，求数列 n 的前n项和． 15nn2  22n1 【答案】（1）a 8n；（2）S 2 ． n n 【解析】 a  设等差数列 n 的公差为d， 因为 a 1， a 6为方程 x2 9x140 的两根，且数列 a n  为递减的等差数列， a 7 1  所以 a 2，  6 a a 27 d  6 1  1 所以 61 61 ， a a (n1)d 7(n1)8n 所以 n 1 ， a  a 8n 即数列 n 的通项公式为 n ． a 8n b 8n2n （2）由（1）得 n ，所以 n ， b  S [76 (8n)]  222  2n 所以数列 n 的前n项和 n  n(78n) 2(12n)   2 12 15nn2  22n1 2 ． 1 a  S 6 19．（2020·毕节市实验高级中学高一期中）已知数列 {a n } 是等差数列,其前n项和为 S n, 3 2 3 . {a } （1）求数列 n 的通项公式； 1 1 1     （2）求和： S S S . 1 2 n n a 2n 【答案】（1） n .（2）n1 【解析】 a  S 3a 12a 4 d a a 642 （1）设等差数列 n 的公差为d,则有： 3 2 2 , 3 2 , a a d 422 1 2 , a  a 22(n1)2n 所以数列 n 的通项公式为： n . n(22n) S  n(n1) （2）由（1）可知： n 2 , 1 1 1 1    ∴S n(n1) n n1, n 1 1 1 1 1 1 1 1 1 n    1      1    ∴S S S 2 2 3 n n1 n1 n1 1 2 n b  b 2b 2,b a a a＝2，a＝4 20．（2020·合肥市第十一中学高一期中）数列 n 满足： n1 n n n1 n，且 1 2 . {b 2} （1）证明数列 n 为等比数列；a  （2）求数列 n 的通项公式. a 2n12n 【答案】（1）证明见解析；（2） n 【解析】 b 2b 2 b 2＝2(b 2) （1）由 n1 n ，得 n1 n b 2  n1 2 b 2 ，又b 2a a 24 n 1 2 1 {b 2}  数列 n 是首项为4，公比为2的等比数列. b 2＝42n1＝2n1，b＝2n1-2 （2）由（1）知， n n ， a a b 2n12 由 n1 n n ， a a b 2n 2(n�2) n n1 n1 ， a a 2n12(n2) n1 n2 ， a a 22 2 …， 2 1 ， a 2  22 23 L 2n 2(n1) n ， 2  2n 1  a   222 23 L 2n 2n2 2n22n12n n 21 . a  n S S 6,S 15 21．（2020·合肥市第十一中学高一期中）已知等差数列 n 的前 项和 n满足 3 5 . a  （1）求 n 的通项公式； a （2）设 b n  2a n n , 求数列 b n  的前n项和T n . 1 n T 2  【答案】（Ⅰ） a n n ；（Ⅱ） n 2n1 2n ．【解析】 a  d a S 6,S 15 （Ⅰ）设等差数列 n 的公差为 ，首项为 1，∵ 3 5 1 3a  3(31)d 6 1 2 { a d 2 a 1 ∴ 5a  1 5(51)d 15 即 { 1 ，解得  1 1 2 a 2d 3 d 1 1 a  a a (n1)d 1(n1)1n ∴ n 的通项公式为 n 1 a n （Ⅱ）由（Ⅰ）得b  n  n 2a n 2n 1 2 3 n1 n T       ∴ n 2 22 23  2n1 2n ① 1 1 1 2 3 n1 n T       ①式两边同乘以2 ，得2 n 22 23 24  2n 2n1 ② 1 1 1 1 1 n T       ①-②得2 n 2 22 23  2n 2n1 1 1  1  2 2n  n 1 n   1  ∴ 1 n 1 1 2n1 2n 2n1 T 2  2 n 2n1 2n 22．（2011·安徽省高三一模（文））设奇函数 对任意 都有 求 和 的值； 数列 满足： ，数列 是等差数列吗？请给予 证明； 【答案】解：（1） ， ；（2）是等差数列. 【解析】 （1）∵ ，且f（x）是奇函数∴ ∴ ，故 因为 ，所以 ． 令 ，得 ，即 ． （2）令 又 两式相加 ． 所以 ， 故 ， 又 ．故数列{a}是等差数列． n