文档内容
专题 4.3 对数
1对数的概念
(1)概念
一般地,如果 ,那么数 叫做以 为底 的对数,记作
ax=N(a>0 , 且a≠1) x a N
x=log N.
a
(a底数, N真数, log N对数)
a
解释 对数log N中对底数a的限制与指数函数y=ax中对a的限制一样.
a
(2) 两个重要对数
常用对数以10为底的对数,log N记为lgN;
10
自然对数以无理数e为底的对数的对数,log N记为ln N.
e
(3) 对数式与指数式的互化
x=log N ⟺ ax=N
a
对数式 指数式
如 ; .
43=64⇔log 64=3 log 25=2⇔52=25
4 5
(4) 结论
① 负数和零没有对数
② log a=1,log 1=0.
a a
特别地,lg10=1,lg1=0,lne=1,ln1=0.
解释 ∵ax=N>0, ∴log N中N>0,如log (−3)没意义;
a 2
由对数式与指数式的互化得 , .
a1=a⇒log a=1 a0=1⇒log 1=0
a a
2 对数的运算性质
如果a>0,a ≠ 1, M>0,N>0 , 有
M
① log (MN)=log M+log N ② log =log M−log N
a a a a N a a
③ ④
log Mn =n log M(n∈R) alog a M=M
a a
(每条等式均可证明)
比较 对数的运算法则与指数的运算法则的联系
指数 对数
am ⋅an=am+n log (MN)=log M+log N
a a aam M
=am−n log =log M−log N
an a N a a
(am) n =amn log Mn =n log M
a a
特别注意: , .
log MN ≠ log M⋅ log N log (M ±N)≠ log M± log N
a a a a a a
一、单选题
1.若 ,则 ( )
A.81 B. C. D.3
【答案】D
【解析】解:因为 ,所以 ,即 ,
所以 ,故选:D.
2.已知 ,则 ( )
A.2 B.3 C. D.
【答案】D
【解析】因为 ,所以 .故选:D
3.已知函效 则 ( )
A.1 B.2 C. D.
【来源】吉林省长春市十一高中2021-2022学年高一上学期第二学程考试数学试题
【答案】B
【解析】由题意知, ,
.故选:B
4.已知函数 是定义在R上的奇函数,当 时, (m为常数),则 的值为( )
A.4 B. C.7 D.
【来源】广东省广州市八校联考2021-2022学年高一下学期期末数学试题
【答案】D
【解析】根据题意,函数 是定义在R上的奇函数,当 时, ,
必有 ,解可得: ,
则当 时, ,有 ,
又由函数 是定义在R上的奇函数,则 .故选:D
5.计算: ( )
A.0 B.1 C.2 D.3
【来源】山西省长治市第四中学校2021-2022学年高一上学期期末数学试题
【答案】B
【解析】解:
;故选:B
6.已知函数 ,则 ( )
A. B. C.1 D.3
【来源】云南省昆明市2021-2022学年高一下学期期末质量检测数学试题
【答案】C
【解析】因为 ,所以 ,
,则 .故选:C.7.设 , ,则
A. B. C. D.
【答案】D
【解析】 , , , ,
则 .故选D.
8.设 ,且 ,则 ( )
A. B. C. D.
【来源】陕西省西安市雁塔区第二中学2021-2022学年高一下学期第二次月考数学试
题
【答案】B
【解析】因为 ,
所以 ,
所以 ,
又 , .故选:B.
9.若 是奇函数,则 ( )
A.2 B. C.3 D.5
【来源】河南省豫北名校2021-2022学年高一下学期第一次联考数学试题
【答案】B
【解析】依题意得: .故选:B
10.函数 的最小值为( )
A.1 B. C. D.【来源】河北省保定市2021-2022学年高一上学期期末数学试题
【答案】D
【解析】由题意得
,
当 时, 的最小值为 .故选:D
11.牛顿冷却定律描述物体在常温环境下的温度变化:如果物体的初始温度为 ,则
经过一定时间t分钟后的温度T满足 ,h称为半衰期,其中 是
环境温度.若 ℃,现有一杯80℃的热水降至75℃大约用时1分钟,那么水温从
75℃降至55℃,大约还需要(参考数据: , , )
( )
A.3.5分钟 B.4.5分钟 C.5.5分钟 D.6.5分钟
【来源】陕西省西安市长安区第一中学2021-2022学年高一下学期期末数学试题
【答案】C
【解析】:由题意, ℃,由一杯80℃的热水降至75℃大约用时1分钟,可得
,
所以 ,
又水温从75℃降至55℃,所以 ,即 ,所以 ,
所以 ,
所以水温从75℃降至55℃,大约还需要 分钟.
故选:C.
12.正数a,b满足1+log a=2+log b=3+log (a+b),则 的值是
2 3 6
A. B. C. D.
【答案】A
【解析】依题意,设1+log a=2+log b=3+log (a+b)=k,则a=2k﹣1,b=3k﹣2,a+b
2 3 6
=6k﹣3,
所以 .故选:A.
13.已知函数 为R上的偶函数,若对于 时,都有 ,且
当 时, ,则 等于( )
A.1 B.-1 C. D.
【来源】四川省自贡市2021-2022学年高一上学期期末数学试题
【答案】A
【解析】当 时, ,则 ,
所以当 时, ,所以
又 是偶函数, ,
所
.故选:A.14.随着社会的发展,人与人的交流变得广泛,信息的拾取、传输和处理变得频繁,
这对信息技术的要求越来越高,无线电波的技术也越来越成熟,其中电磁波在空间中
自由传播时能量损耗满足传输公式: ,其中D为传输距离,
单位是 ,F为载波频率,单位是 ,L为传输损耗(亦称衰减)单位为 .若
传输距离变为原来的4倍,传输损耗增加了 ,则载波频率变为原来约( )倍
(参考数据: )
A.1倍 B.2倍 C.3倍 D.4倍
【来源】广东省广州市华南师范大学附属中学2021-2022学年高一下学期期末数学试
题
【答案】B
【解析】设 是变化后的传输损耗, 是变化后的载波频率, 是变化后的传输距
离,则 , ,
,
则 ,即 ,从而 ,
即载波频率变为原来约2倍.故选:B.
二、填空题
15.已知函数 ( 且 ),且 ,则
___________.
【答案】
【解析】因为 ,则 ,
化为对数式,可得 ,
所以 ,故答案为: .
16.计算: _________.
【来源】四川省泸州市泸县第一中学2021-2022学年高一下学期开学考试数学试题
【答案】【解析】原式
.
故答案为:
17.若 , 且 ,则 的值___.
【答案】 【解析】 , 且 ,
, ,
.
故答案为:0.
18. ___.
【答案】
【解析】
= 9
.故答案为:102.
19. = ________
【来源】第11讲 对数-【暑假自学课】2022年新高一数学暑假精品课(苏教版2019
必修第一册)【答案】
【解析】
故答案为:
20. __________.
【来源】河南省信阳市信阳高级中学2021-2022学年高一下学期第一次月考数学(理
科)试题
【答案】6
21.如果关于 的方程 的两根分别是 ,则
的值是__________.
【来源】第4章 指数与对数综合测试-【暑假自学课】2022年新高一数学暑假精品课
(苏教版2019必修第一册)
【答案】
【解析】∵ 是关于 的方程 的两根
∴ 是一元二次方程 的两根
∴ ,
∴ .
故答案为:
22.已知定义在R上的函数 满足 ,且当 时,
,若对任 都有 ,则m的取值范围是_________.【来源】河南省信阳市信阳高级中学2021-2022学年高一下学期第一次月考数学(理
科)试题
【答案】 , .
【解析】:因为 满足 ,即 ;
又由 ,可得 ,
画出当 , 时, 的图象,
将 在 , 的图象向右平移 个单位(横坐标不变,纵坐标变为原来的2
倍),再向左平移 个单位(横坐标不变,纵坐标变为原来的 倍),
由此得到函数 的图象如图:
当 , 时, , , ,
又 ,所以 ,
令 ,由图像可得 ,则 ,解得 ,
所以当 时,满足对任意的 , ,都有 ,
故 的范围为 , .
故答案为: , .
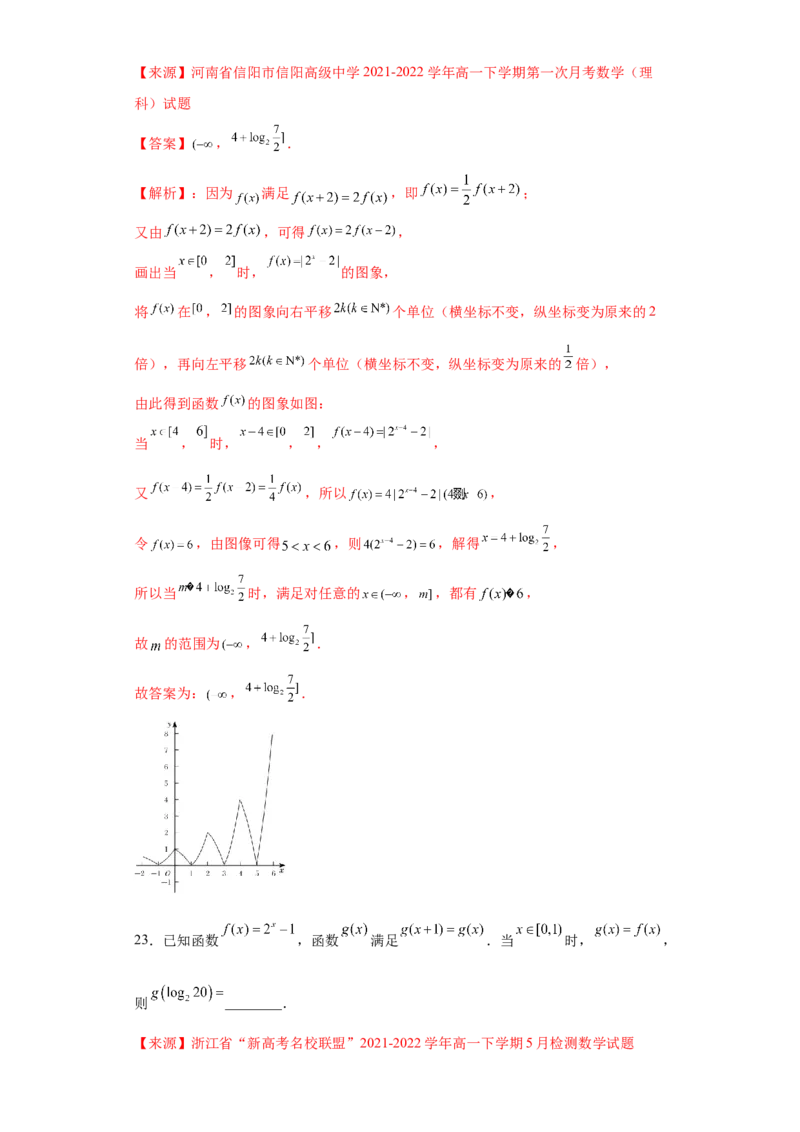
23.已知函数 ,函数 满足 .当 时, ,
则 ________.
【来源】浙江省“新高考名校联盟”2021-2022学年高一下学期5月检测数学试题【答案】 ##
【解析】:因为函数 满足 ,又 ,
则 ,
又 时
所以 ;
故答案为:
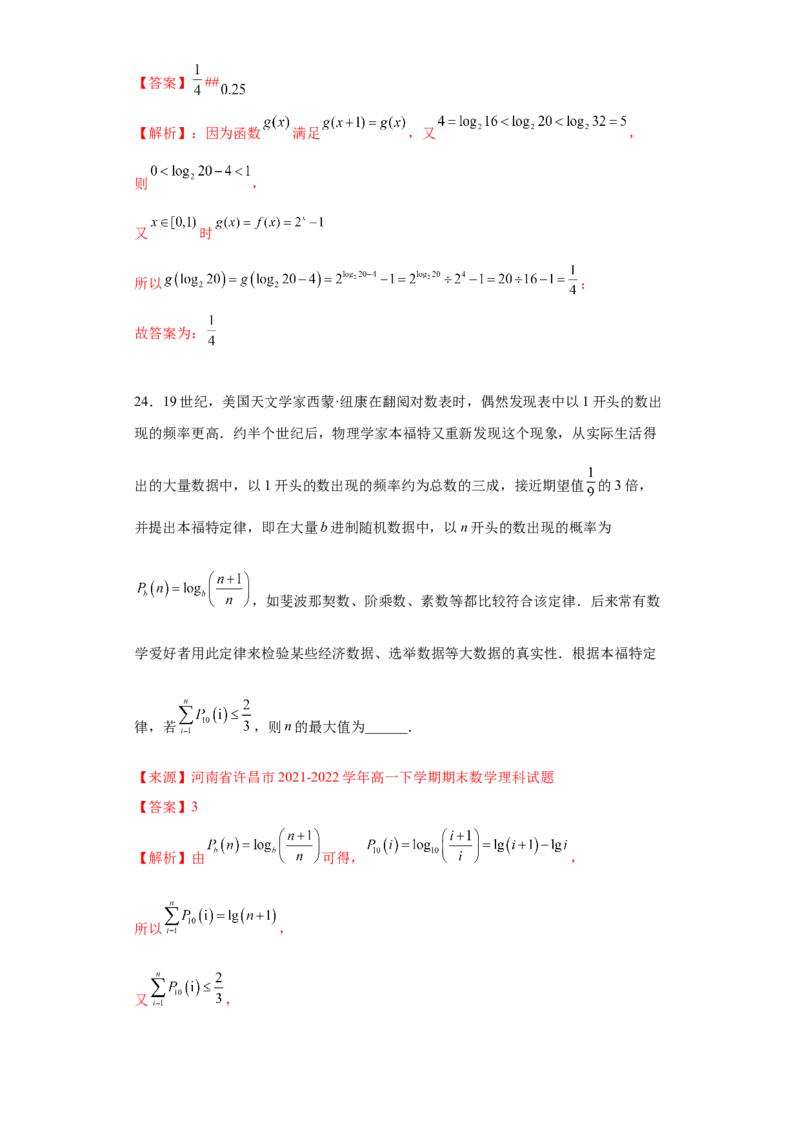
24.19世纪,美国天文学家西蒙·纽康在翻阅对数表时,偶然发现表中以1开头的数出
现的频率更高.约半个世纪后,物理学家本福特又重新发现这个现象,从实际生活得
出的大量数据中,以1开头的数出现的频率约为总数的三成,接近期望值 的3倍,
并提出本福特定律,即在大量b进制随机数据中,以n开头的数出现的概率为
,如斐波那契数、阶乘数、素数等都比较符合该定律.后来常有数
学爱好者用此定律来检验某些经济数据、选举数据等大数据的真实性.根据本福特定
律,若 ,则n的最大值为______.
【来源】河南省许昌市2021-2022学年高一下学期期末数学理科试题
【答案】3
【解析】由 可得, ,
所以 ,
又 ,所以, ,即
所以,
则n的最大值为 .
故答案为: .