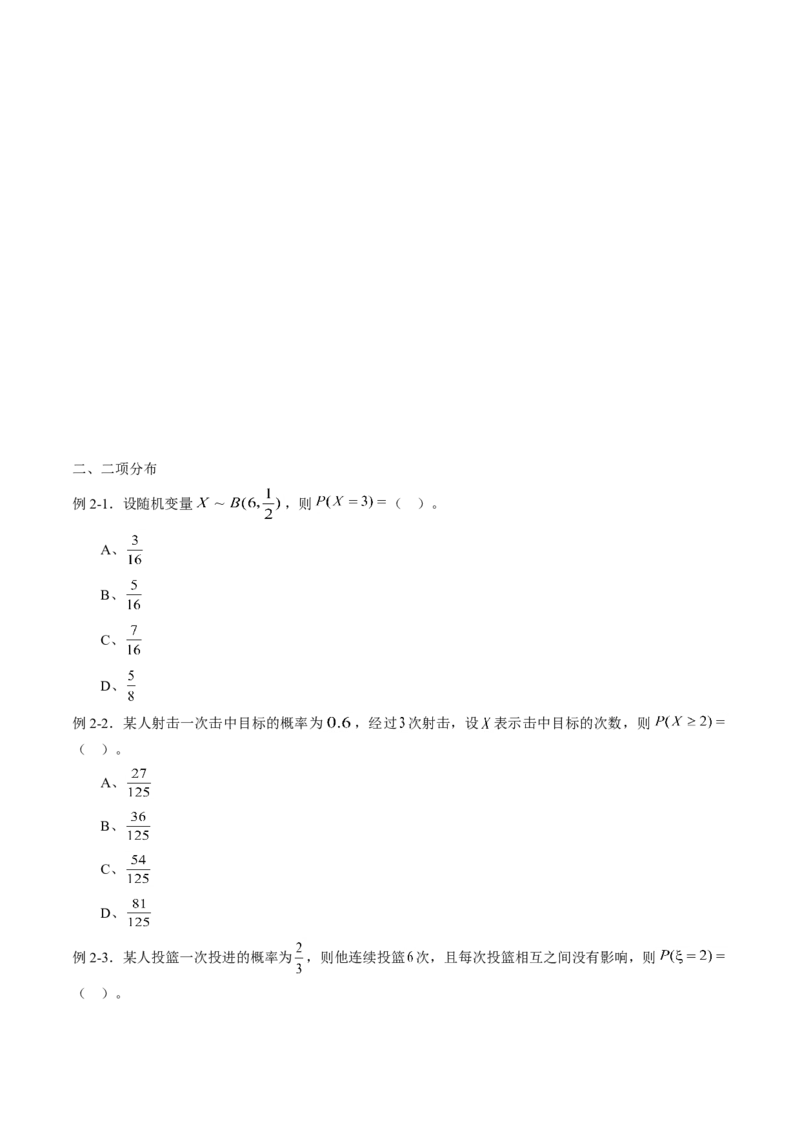文档内容
专题 7.4 二项分布与超几何分布
姓名: 班级:
重点 二项分布与超几何分布的特征
难点 二项分布与超几何分布的计算
一、超几何分布
例1-1.一工厂生产的100个产品中有90个一等品,10个二等品,现从这批产品中抽取4个,则其中恰好
有一个二等品的概率为( )。
A、
B、
C、
D、
例1-2.有 名学生,其中有 名男生。从中选出 名代表,选出的代表中男生人数为 ,则其数学期望为
( )。
A、
B、
C、
D、
例1-3.在含有 件次品的 件产品中,任取 件, 表示取到的次品数,则 。
例1-4.一个盒子装有 个红、白两色同一型号的乒乓球,已知红色乒乓球有 个,若从盒子里随机取出
个乒乓球,则其中含有红色乒乓球个数的数学期望 。
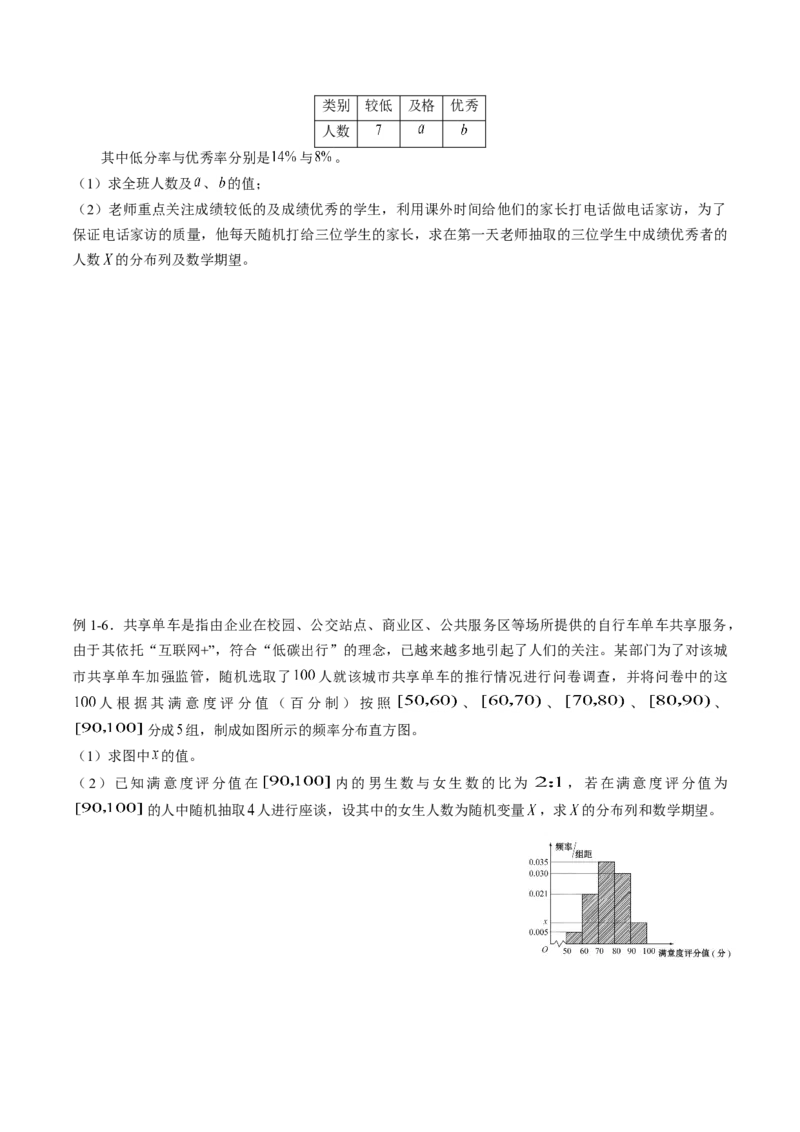
例1-5.期中考试后,老师把学生的成绩分为较低、及格(不含优秀)、优秀三类,制成下表。类别 较低 及格 优秀
人数
其中低分率与优秀率分别是 与 。
(1)求全班人数及 、 的值;
(2)老师重点关注成绩较低的及成绩优秀的学生,利用课外时间给他们的家长打电话做电话家访,为了
保证电话家访的质量,他每天随机打给三位学生的家长,求在第一天老师抽取的三位学生中成绩优秀者的
人数 的分布列及数学期望。
例1-6.共享单车是指由企业在校园、公交站点、商业区、公共服务区等场所提供的自行车单车共享服务,
由于其依托“互联网+”,符合“低碳出行”的理念,已越来越多地引起了人们的关注。某部门为了对该城
市共享单车加强监管,随机选取了 人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这
人根据其满意度评分值(百分制)按照 、 、 、 、
分成 组,制成如图所示的频率分布直方图。
(1)求图中 的值。
(2)已知满意度评分值在 内的男生数与女生数的比为 ,若在满意度评分值为
的人中随机抽取 人进行座谈,设其中的女生人数为随机变量 ,求 的分布列和数学期望。二、二项分布
例2-1.设随机变量 ,则 ( )。
A、
B、
C、
D、
例2-2.某人射击一次击中目标的概率为 ,经过 次射击,设 表示击中目标的次数,则
( )。
A、
B、
C、
D、
例2-3.某人投篮一次投进的概率为 ,则他连续投篮 次,且每次投篮相互之间没有影响,则
( )。A、
B、
C、
D、
例2-4.已知随机变量 、 满足 ,且 ,若 ,则 ( )。
A、
B、
C、
D、
例2-5.已知离散型随机变量 服从二项分布 ,且 , ,则 的最小
值为( )。
A、
B、
C、
D、
例2-6.某群体中的每位成员使用移动支付的概率都为 ,各成员的支付方式相互独立,设 为该群体的
位成员中使用移动支付的人数, , ,则 ( )。
A、
B、
C、
D、
例2-7.已知随机变量 ,若 、 ,则 的值为 。
例2-8.一批产品的二等品率为 ,从这批产品中每次随机取一件,有放回地抽取 次, 表示抽到
的二等品件数,则 。例2-9.张明要参加某单位组织的招聘面试。面试要求应聘者有 次选题答题的机会(选一题答一题),若
答对 题即终止答题,直接进入下一轮,否则被淘汰。已知张明答对每一道题的概率都为 。
(1)求张明进入下一轮的概率;
(2)设张明在本次面试中答题的个数为 ,试写出 的分布列,并求 的数学期望。
例2-10.一名学生每天骑车上学,从他家到学校的途中有 个交通岗,假设他在各个交通岗遇到红灯的事
件是相互独立的,并且概率都是 。
(1)设 为这名学生在途中遇到红灯的次数,求 的分布列、期望、方差;
(2)设 为这名学生在首次停车前经过的路口数,求 的分布列;
(3)求这名学生在途中至少遇到一次红灯的概率。