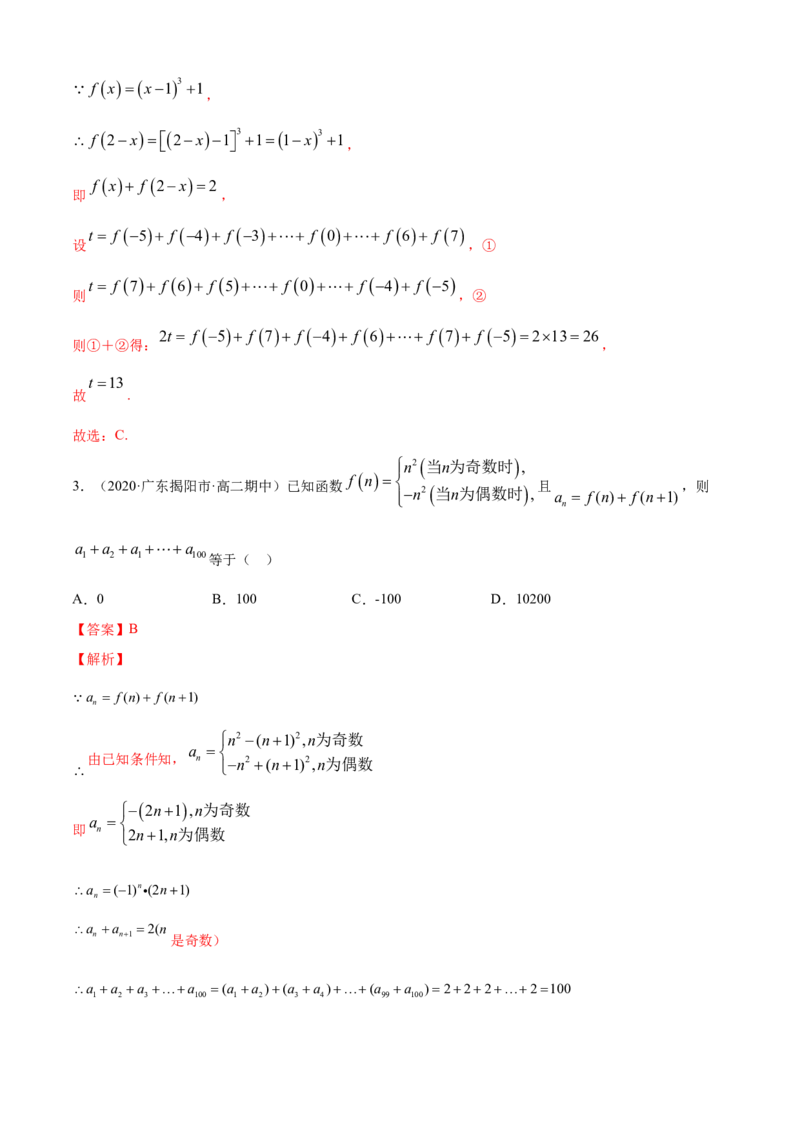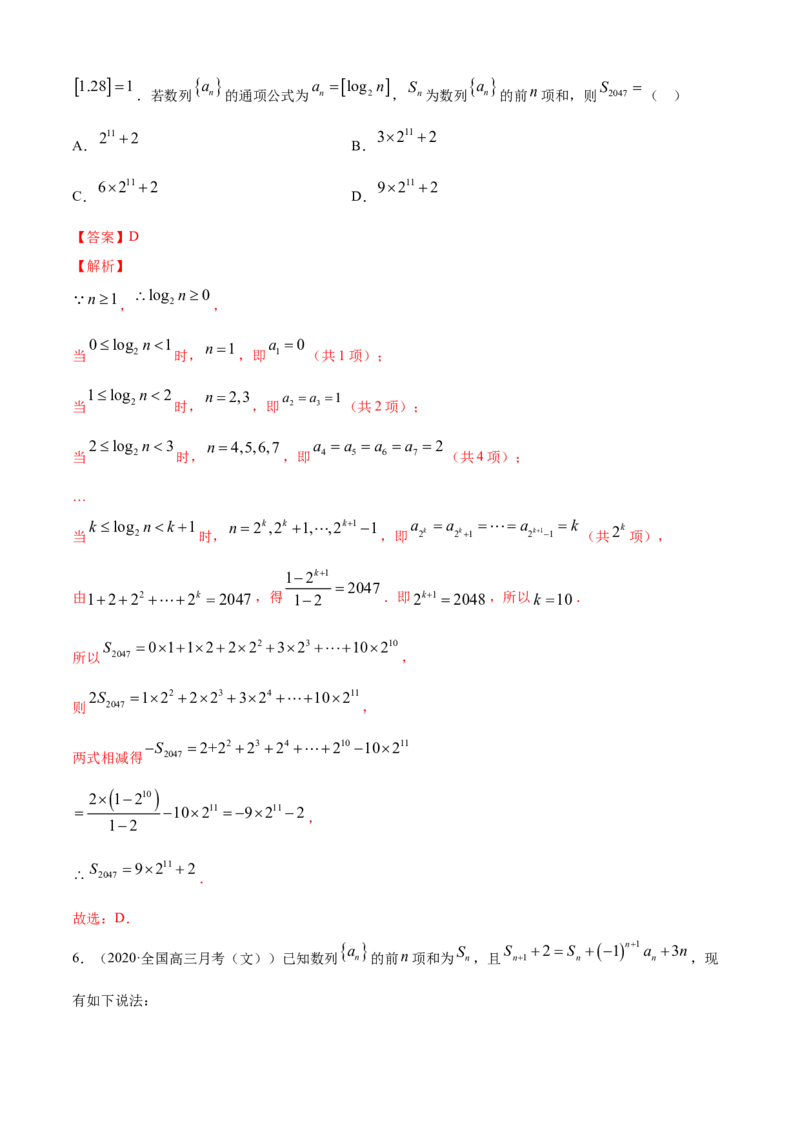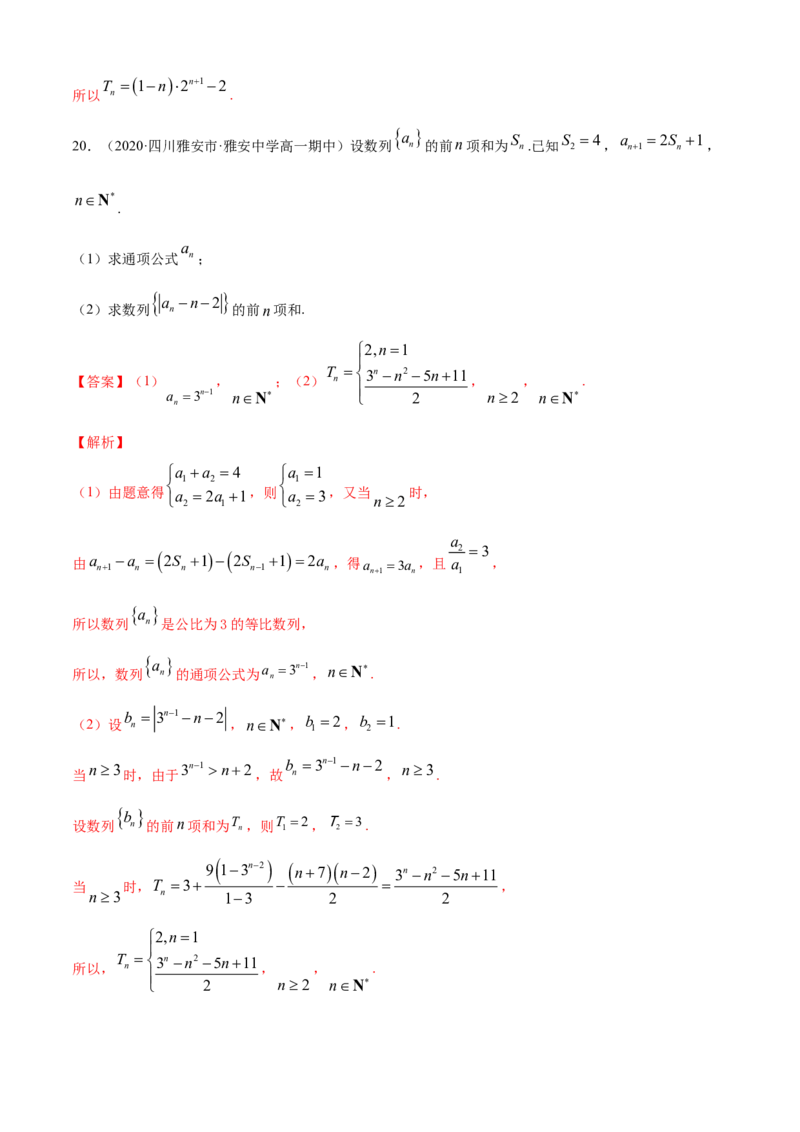专题4.4数列的求和（B卷提升篇）解析版_E015高中全科试卷_数学试题_选修2_01.同步练习_同步练习（第四套）_专题4.4数列的求和（B卷提升篇）

专题4. 4数列的求和（B 卷提升篇）（人教A版第二册,浙江专用） 参考答案与试题解析 第Ⅰ卷（选择题） 一．选择题（共10小题，满分50分，每小题5分） 1 1 1 1 1．（2020·全国高二课时练习）设数列 a n  的前n项和 S n  3 n  n2 1  ，则数列a 2 , a 3 ,  , a n1 ,  的前 n项和为（ ） n1 n1 n n A． n B． n C．n1 D．n1 【答案】D 【解析】 1 S  n  n2 1  因为 n 3 ， 1 1 a S S  n  n2 1   (n1)(n1)2 1 n(n1) 所以 n n n1 3 3   ，n2， 1 1 1 1    因此a n(n1) n1 n， n 1 1 1  1 1 1 1 1  1 n  ...  1   ...  1        所以a a a  2 2 3 n n1 n1 n1. 2 3 n1 故选:D f xx13 1 2．（2020·成都市实验外国语学校（西区）高一期中）已知函数 ，利用课本中推导等差 f 5 f 4 f 0 f 6 f 7 n 数列的前 项和的公式的方法，可求得 （ ）. 25 A．25 B．26 C．13 D． 2 【答案】C 【解析】f xx13 1  ，  f 2x2x1 3 11x3 1   ， f x f 2x2 即 ， t  f 5 f 4 f 3 f 0 f 6 f 7 设 ，① t  f 7 f 6 f 5 f 0 f 4 f 5 则 ，② 2t  f 5 f 7 f 4 f 6 f 7 f 521326 则①＋②得： ， t 13 故 . 故选：C. n2当n为奇数时,  3．（2020·广东揭阳市·高二期中）已知函数 f n  n2当n为偶数时, 且 a  f(n) f(n1) ，则 n a a a  a 1 2 1  100等于（ ） A．0 B．100 C．-100 D．10200 【答案】B 【解析】 a  f(n) f(n1)  n n2 (n1)2,n为奇数 a   由已知条件知， n n2 (n1)2,n为偶数 2n1,n为奇数 a  即 n 2n1,n为偶数 a (1)n (2n1) n  a a 2(n n n1 是奇数） a a a a (a a )(a a )(a a )2222100 1 2 3 100 1 2 3 4 99 100故选：B． 4．（2020·浙江宁波市·高三期中）公元1202年列昂那多·斐波那契（意大利著名数学家）以兔子繁殖为 a  a 1 a 1 例，引入“兔子数列” n ：1，1，2，3，5，8，13，21，34，55，……，即 1 ， 2 ， a a a  nN*,n2  n n1 n2 ，此数列在现代物理、化学等学科都有着十分广泛的应用。若将此数列 a  b  b  n T a  n 的各项除以2后的余数构成一个新数列 n ，设数列 n 的前 项的和为 n；若数列 n 满足： c a2 a a c  n S T S  n n1 n n2，设数列 n 的前 项的和为 n，则 2020 2020 （ ） A．1348 B．1347 C．674 D．673 【答案】B 【解析】   “兔子数列”的各项为：1，1，2，3，5，8，13，21，34，55， ，   此数列被2除后的余数依次为：1，1，0，1，1，0，1，1，0， ， b 1 b 1 b 0 b 1 b 1 b 0  即 1 ， 2 ， 3 ， 4 ， 5 ， 6 ， ， {b }  数列 n 是以3为周期的周期数列， T 673(b b b )b 673211347 2020 1 2 3 1 ， c a 2 a (a a ) a (a a )a 2 a a a 2 n1  n2 n1 n1 n2  n2 n2 n1 n1  n n2 n1 1 由题意知 c a 2 a a a 2 a a a 2 a a ， n n1 n n2 n1 n n2 n1 n n2 c a2 aa 1 由于 1 2 1 3 ， c (1)n 所以 n ， S (11)(11)(11)0 所以 2020 ． T S 1347 则 2020 2020 ． 故选：B x 0.390 x 5．（2020·河南商丘市·高三其他模拟（理））定义 表示不超过 的最大整数，如 ，1.281 a  a log n S a  n S  ．若数列 n 的通项公式为 n 2 ， n为数列 n 的前 项和，则 2047 （ ） 2112 32112 A． B． 62112 92112 C． D． 【答案】D 【解析】 n1 log n0  ， 2 ， 0log n1 a 0 n1 当 2 时， ，即 1 （共1项）； 1log n2 n2,3 a a 1 当 2 时， ，即 2 3 （共2项）； 2log n3 n4,5,6,7 a a a a 2 当 2 时， ，即 4 5 6 7 （共4项）； … 当 k log 2 nk1 时， n2k,2k 1,,2k11 ，即 a 2k a 2k1 a 2k11 k （共 2k 项）， 12k1 2047 由1222 2k 2047，得 12 ．即2k1 2048，所以k 10． S 0112222 32310210 所以 2047 ， 2S 122 223324 10211 则 2047 ， S 2+22 2324 210 10211 两式相减得 2047 2  1210  10211 92112 ， 12 S 92112  2047 ． 故选：D． 6．（2020·全国高三月考（文））已知数列 a n  的前n项和为 S n，且 S n1 2S n 1n1 a n 3n ，现 有如下说法：a a a a 12n1 S 1220 ① 5 41；② 2n 2n2 ；③ 40 . 则正确的个数为（ ） A．0 B．1 C．2 D．3 【答案】D 【解析】 S 2S 1n1 a 3n 因为 n1 n n ， a 1n1 a 3n2 所以 n1 n ， a a 6k21 a a 6k52 所以 2k1 2k ， 2k 2k1 ， a a 33 联立得： 2k1 2k1 ， a a 34 所以 2k3 2k1 ， a a 故 2k3 2k1， a a a a 从而 1 5 9 41， a a 6k 2 a a 6k1 2k 2k1 ， 2k2 2k1 ， a a 12k1 S a a a a a ...a a a 则 2k 2k2 ，故 40 1 2 3 4 5 38 39 40， a a a a ...a a a a  2 3 4 5 38 39 40 41 ， 20 411820 6k2  2 1220 ， k1 故①②③正确. 故选：D a  S a 1 a 2S n 7．（2020·江苏南通市·高三期中）已知数列 n 的前n项和为 n， 1 ，当 n2 时， n n1 ，，则S 的值为（ ） 2019 A．1008 B．1009 C．1010 D．1011 【答案】C 【解析】a 2S n n2 当 时， n n1 ，① a 2S n1 可得 n1 n ，② a a 2(S S )1 a a 1n2 由②－①得， n1 n n n1 ，整理得 n1 n ， a 1 又由 1 S a (a a )(a a ) (a a )1010 所以 2019 1 2 3 4 5  2018 2019 . 故选：C. 8．（2020·广东广州市·增城中学）已知 a n  的前 n 项和为 S n， a 1 1 ，当 n2 时， a n 2S n1 n ，则 S 2019的值为（ ） A．1008 B．1009 C．1010 D．1011 【答案】C 【解析】 S S a n2 由题意，当 时，可得 n1 n n， a 2S n a 2(S a )n 2S a n 因为 n n1 ，所以 n n n ，即 n n ， 2S a n1 n2 当 时， n1 n1 2a a a 1 a a 1 两式相减，可得 n n n1 ，即 n n1 ， a a 1,a a 1,a a 1, 所以 2 3 4 5 6 7  ， 20191 S a a a a a  a a 1 11010 所以 2019 1 2 3 4 5  2018 2019 2 . 故选：C. 1 9．（2020·广东深圳市·深圳外国语学校高三月考）已知数列 a n  满足： a 1  2， a n1 a n 2 a n ，用 x 1 1 1 1       表示不超过 的最大整数，则 a 1 a 1 a 1 a 1 的值等于（ ） x   1 2 2020 2021 A．1 B．2 C．3 D．4 【答案】A 【解析】 1 1 1   由a a2 a ，得a 1 a a ， n1 n n n n n1 1 1 1   ∴a 1 a 1 a 1， 1 2 2021 1 1 1 1 1 1       a a a a a a ， 1 2 2 3 2021 2022 1 1 1   2 a a a ， 1 2022 2022 1 1 3 21 a  a  a  a  1 由 1 2， a a2 a 得 1 2， 2 4， 3 16 知从 a 以后都大于1， n1 n n 3 1 0,1 ∴a ， 2022 1 2 1,2 ∴ a ， 2022  1 1 1    1   则 a 1 a 1 a 1 ，   1 2 2012 故选：A. 10．（2020·山西高三期中（理））若数列 a n  的通项公式为 a n 2n 1 ，在一个 n 行 n 列的数表中，第i j c a a a a i 1,2,,n, j 1,2,,n c c c 2021 n 行第 列的元素为 ij i j i j ，则满足 11 22 nn 的 的最大值是（ ） 4 5 6 7 A． B． C． D．【答案】B 【解析】 数列 a n  的通项公式为 a n 2n 1 ，在一个 n 行 n 列的数表中，第i行第 j 列的元素为 c a a a a i 1,2,,n, j 1,2,,n ij i j i j ， c a a a a   2i 1  2j 1  2i 12j 12ij 1 所以 ij i j i j ． S c c  c S S c 0  n2,nN S  令 n 11 22  nn，则 n n1 nn ，所以，数列 n 为递增数列， c c  c 2021 当 11 22  nn 时， S 22 124 126 1 2nn 12021 所有的元素之和为 n  ， S 22 24 26 28 43362021 n4 当 时， 4 ， S 22 24 26 28 210 513592021 n5 当 时， 5 ， n6 S 22 24 26 28 210 212 654542021 当 时， 6 ， n 5 故 的最大值为 ， 故选：B． 第Ⅱ卷（非选择题） 二．填空题（共7小题，单空每小题4分，两空每小题6分，共36分） 11．（2020·四川雅安市·雅安中学高一期中）数列 的通项公式为 ，其前2020 项的和为______. 【答案】 【解析】 ，∴ ， ，， ， ， ， ， ， 由上可知，数列 的奇数项为-1，偶数项 ， ， . 故答案为： ． 12．（2020·山西省榆社中学高三月考（理））已知 ，集合 ，集合 的所有非空子集的最小元素之和为 ，则使得 的最小正整数n的值为______． 【答案】13 【解析】 当 时， 的所有非空子集为： ， ， ，所以 . 当 时， . 当 时，当最小值为 时，每个元素都有或无两种情况，共有 个元素，共有 个非空 子集， . 当最小值为 时，不含 ，含 ，共有 个元素， 有 个非空子集， .…… 所以 … … . 因为 ， ，即 . 所以使得 的最小正整数 的值为 . 故答案为： . 13．（2020·上海市洋泾中学高三期中）已知公比大于 的等比数列 满足 ，记 为 在区间 中的项的个数， 的前 项和为 ，则 __________. 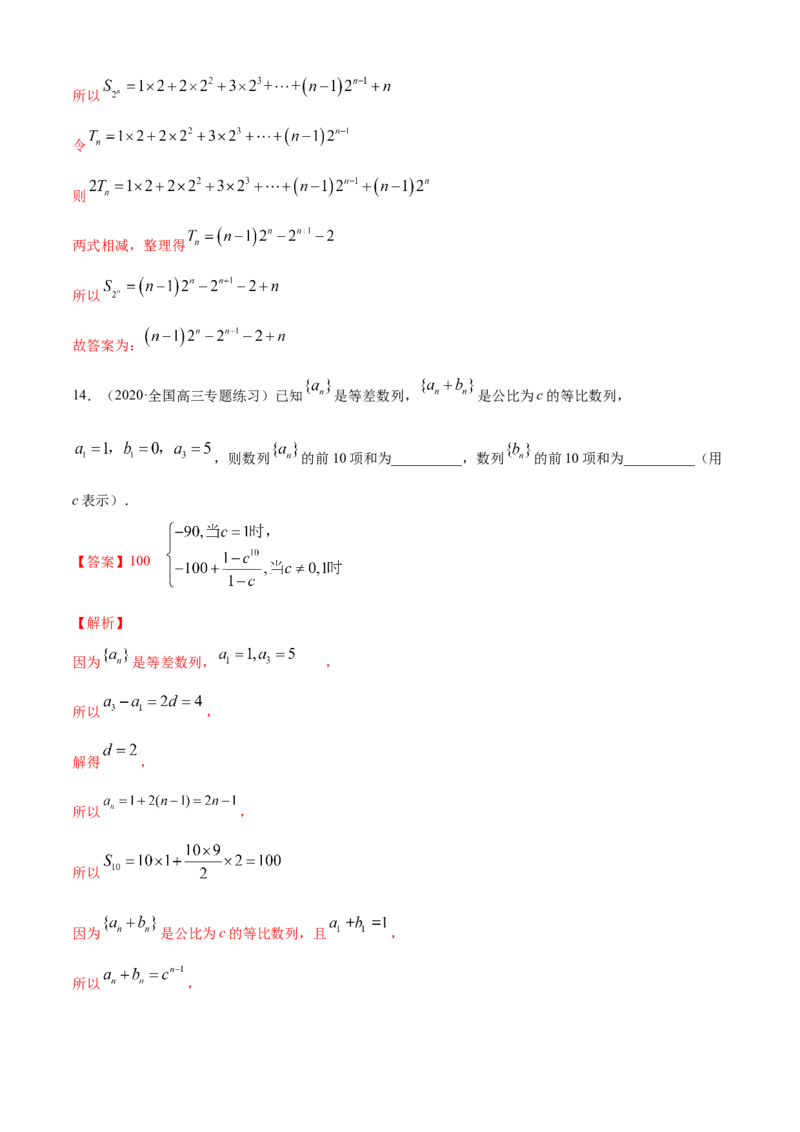【答案】 【解析】 设 的公比为 ，由 得 或 （舍去） 所以 在区间 上， ， 在区间上 上 ， 个1 在区间 上， ， 个2 在区间 上， ， 个3， … 归纳得当 时，所以 令 则 两式相减，整理得 所以 故答案为： 14．（2020·全国高三专题练习）已知 是等差数列， 是公比为c的等比数列， ，则数列 的前10项和为__________，数列 的前10项和为__________（用 c表示）． 【答案】100 【解析】 因为 是等差数列， ， 所以 ， 解得 ， 所以 ， 所以 因为 是公比为c的等比数列，且 ， 所以 ，故 ， 当 时， ， 当 时， ， 综上 , 故答案为：100； 15．（2020·江苏苏州市·周市高级中学高二月考）已知数列 的前 项和为 ，满足 ，则数列 的通项公式 ______.设 ，则数列 的前 项 和 ______. 【答案】 【解析】 因为 ，所以当 时， ， 当 时， ，符合 的情况，所以 ； 因为 ，当 为偶数时， ， 所以 ， 当 为奇数时， ，所以 ， 综上可知 . 故答案为： ； . 16．（2020·海南高三期中）已知数列 的前 项和为 ，且 ， ，则 ______； 若 恒成立，则实数 的取值范围为______. 【答案】 【解析】 由 ， ，得 ， ， 所以数列 是首项为1，公比为 的等比数列， 所以 ， ，. 又 ，所以 恒成立， 即 ， 恒成立. 令 ，则 ，所以 是递减数列， 所以 ， ，即 ， 实数 的取值范围为 . 故答案为： ； . 17．（2020·福建莆田二中高二月考）“斐波那契数列”是数学史上一个著名数列，从第三项开始每一项都 是数列中前两项之和.这个数列是斐波那契在他的《算盘书》的“兔子问题”中提出的.在问题中他假设如 果一对兔子每月能生一对小兔（一雄一雌），而每对小兔在它出生后的第三个月，又能开始生小兔，如果 没有死亡，由一对刚出生的小兔开始，一年后一共会有多少对兔子？即斐波那契数列 中， ， , ，则 ______；若 ，则数列 的前 项和是_______ （用 表示）. 【答案】144 【解析】 由 ， , ，依次可求出 的值，利用用累加法可求出数列 的前 项和 【详解】解：因为 ， , ， 所以 ，同理 ， 因为 ， , ， 所以 …… 以上累加得， ， 所以 ， 故答案为：144； 三．解答题（共5小题，满分64分，18--20每小题12分，21,22每小题14分） a  n S 18．（2020·威远中学校高三月考（理））已知数列 n 是等差数列，前 项和为 n，且 S 3a ,a a 8 5 3 4 6 . a （1）求 n； （2）设 b n 2na n，求数列 b n  的前 n 项和 T n . 【答案】（1） a n 2n3 nN* ；（2） T n (n4)2n2 16 . 【解析】5(a a ) （1）由题意，数列 a n  是等差数列，所以 S 5  1 2 5 5a 3， S 3a a 0 又 5 3，所以 3 ， a a 82a a 4 由 4 6 5，解得 5 ， a a 2d 4 d 2 所以 5 3 ，解得 ， 所以数列的通项公式为 a n a 3 n3d 2n3 nN* . b 2na n32n1 （2）由（1）得 n n ， T 222 123024  n32n1 n  ， 2T 223124  n42n1n32n2 n  ， 2T T 222   2324  2n1 n32n2 两式相减得 n n  ， 8  12n1 8 (n3)2n2 (n4)2n2 16 ， 12 T (n4)2n2 16 所以 n . a  S na n1a 19．（2020·湖南衡阳市一中高三期中）设数列 n 的前n项和为 n，从条件① n1 n，② n1a S n  2 n ，③a n 2 a n 2S n 中任选一个，补充到下面问题中，并给出解答.已知数列 a n  的前n项和 S a 1 为 n， 1 ，____. a  （1）求数列 n 的通项公式； b 2na b  T （2）若 n n，求数列 n 的前n和 n. 【答案】（1）答案见解析；（2）答案见解析. 【解析】选条件①时， a a a n1  n  1 1 na n1a （1） n1 n时，整理得n1 n 1 ， a n 所以 n . b n2n （2）由（1）得： n ， c n2n n C 设 n ，其前 项和为 n， C 121222  n2n 所以 n  ①， 2C 122 223 n2n1 n  ②， 2  2n 1  C   2122  2n n2n1  n2n1 ①  ②得： n  21 ， C n12n12 故 n ， T 1n2n12 所以 n . 选条件②时， n1a S  n （1）由于 n 2 ， 2S n1a 2S na n2 所以 n n①，当 时， n1 n1②， 2a n1a na ①②得： n n n1， n1a na n n1， a a a n  n1  n 1 整理得 n n1 1 ， a n 所以 n . b n2n （2）由（1）得： n ，c n2n n C 设 n ，其前 项和为 n， C 121222  n2n 所以 n  ①， 2C 122 223 n2n1 n  ②， 2  2n 1  C   2122  2n n2n1  n2n1 ①  ②得： n  21 ， C n12n12 故 n ， T 1n2n12 所以 n . 选条件③时， a2 a 2S 由于 n n n， ① a2 a 2S n1 n1 n1 ② a2 a2 a a  a a 1 ①②时， n n1 n n1 ，整理得 n n1 （常数）， a  所以数列 n 是以1为首项，1为公差的等差数列. a n 所以 n . b n2n （2）由（1）得： n ， c n2n n C 设 n ，其前 项和为 n， C 121222  n2n 所以 n  ①， 2C 122 223 n2n1 n  ②， 2  2n 1  C   2122  2n n2n1  n2n1 ①  ②得： n  21 ， C n12n12 故 n ，T 1n2n12 所以 n . 20．（2020·四川雅安市·雅安中学高一期中）设数列  a n  的前n项和为 S n.已知 S 2 4 ， a n1 2S n 1 ， nN . a （1）求通项公式 n；   a n2 （2）求数列 n 的前n项和. 2,n1  T 3n n2 5n11 【答案】（1） ， ；（2） n ， ， .  a 3n1 nN  2 n2 nN n 【解析】 a a 4 a 1 1 2 1   （1）由题意得 a 2a 1，则 a 3，又当 时，   n2 2 1 2 a 2 3 由a n1 a n   2S n 1  2S n1 12a n ，得a n1 3a n ，且 a 1 ， a  所以数列 n 是公比为3的等比数列， 所以，数列  a n  的通项公式为a 3n1 ，nN . n （2）设 b n  3n1n2 ，nN，b 1 2，b 2 1. n3 3n1 n2 b 3n1n2 n3 当 时，由于 ，故 n ， .  b  设数列 n 的前n项和为T n ，则T 1 2，T 2 3. 9  13n2  n7 n2 3n n2 5n11 当 时，T 3   ， n3 n 13 2 2 2,n1  T 3n n2 5n11 所以， n ， ， .   2 n2 nNa  n S a 1 a 2S 1nN  21．（2020·浙江高三月考）已知数列 n 的前 项和为 n，且 1 ， n1 n  ，数列 b  b 1 b b a n 满足 1 ， n1 n n. a  b  （1）求数列 n 、 n 的通项公式； a c  n （2）若数列 c n  满足 n b n b n1 且c 1 c 2 L c n 2b n 11对任意nN + 恒成立，求实数的 取值范围. 3n11  1 【答案】（1）a n 3n1nN   ， b n  2 ；（2）   , 2  . 【解析】 a 2S 1 a 2S 1 a 3a （1）本题首先可根据 n1 n 得出 n n1 ，然后两式相减，得出 n1 n， a 1 a 2S 1nN  a 2S 1nN ,n2 （1）因为 1 ， n1 n  ，所以 n n1  ， a a 2S S  a a 2a a 3a nN ,n2 则 n1 n n n1 ，即 n1 n n， n1 n  ， a 2a 13 a 3a 因为 2 1 ， 2 1， a  a 3n1nN  所以数列 n 是以1为首项、 3 为公比的等比数列， n  ， b b a b b 3n1 b b 3n1 因为 n1 n n，所以 n1 n ，即 n1 n ， b b b b b  b b b 则 n n n1 n1 n2  2 1 1 30  13n1 3n11 3n2 3n3L 30 1 1 . 13 2 a 3n1 43n1  1 1  c  n   2    n b b 3n11 3n 1  3n11  3n 1  3n11 3n 1 （2） n n1  ，      2   2  T c c c L c 令 n 1 2 3 n， 1 1   1 1   1 1  T 2        L     则 n 30 1 311 311 32 1 3n11 3n 1 1 1  2 2  1   2 3n 1 3n 1， T 2b 11 nN 因为 n n 对任意 +恒成立， 2  3n11  1 2 11 所以 3n 1  2  对任意 nN 恒成立， +   2   即   3n 1  3n1 ，   min 2 2 y   令  3n 1  3n1 3  3n12 3n1 ， ， t 3n1 1 2 1 y   则 3t2 t ，当t 1时，即当n1时取到最小值 2 ， 1  1   ,  故 2 ，实数的取值范围为 2. a  n S 22．（2020·四川师范大学附属中学高一期中（理））已知各项都是正数的数列 n 的前 项和为 n， 1 S a2  a n n 2 n，nN*. a  （1）求数列 n 的通项公式.  1    （2）设数列b 满足： b 1 ，b b 2a n2，数列  b  的前 n 项和 T .求证： T 2 . n 1 n n1 n n n n 1 a  n 【答案】（1） n 2 ；（2）证明见解析. 【解析】 n1 （1）①当 时，1 1 S a2  a a a2  a 得 1 1 2 1， 1 1 2 1 1 a  ∴ 1 2或0（舍去）； 1 S a2  a ②当n2时， n1 n1 2 n1， 1 1 a S S a2  a a2  a ∴ n n n1 n 2 n n1 2 n1 1 1 a2 a2  a  a 0 n n1 2 n 2 n1 1 a a a a  a a 0 n n1 n n1 2 n n1  1 a a  a a  0   n n1  n n1 2 . a  又∵ n 各项为正， 1 1 a a  0 a a  ∴ n n1 2 ， n n1 2 1 1 ∴a 为首项是 ，公差是 的等差数列， n 2 2 1 a a n1d  n ∴ n 1 2 . b b n （2）由题得， n n1 b b n1 n1 n2 ┇ b b 3 3 2 b b 2 2 1 ， 所有式子相加，b b 23n1n 得 n 1 n1n2 n2 n2   2 2 . n2 n b  又∵b 1，∴ n 2 ， 1 1 2 2 1 1    2    ∴b n2 n nn1 n n1， n 1 1 1 1 1 1  T 2        ∴ n 1 2 2 3 n n1  1  2 2 1 2    n1 n1. 又∵n10， T 2 ∴ n .