文档内容
专题 5.4 三角函数图像与性质
y=sinx,x∈R
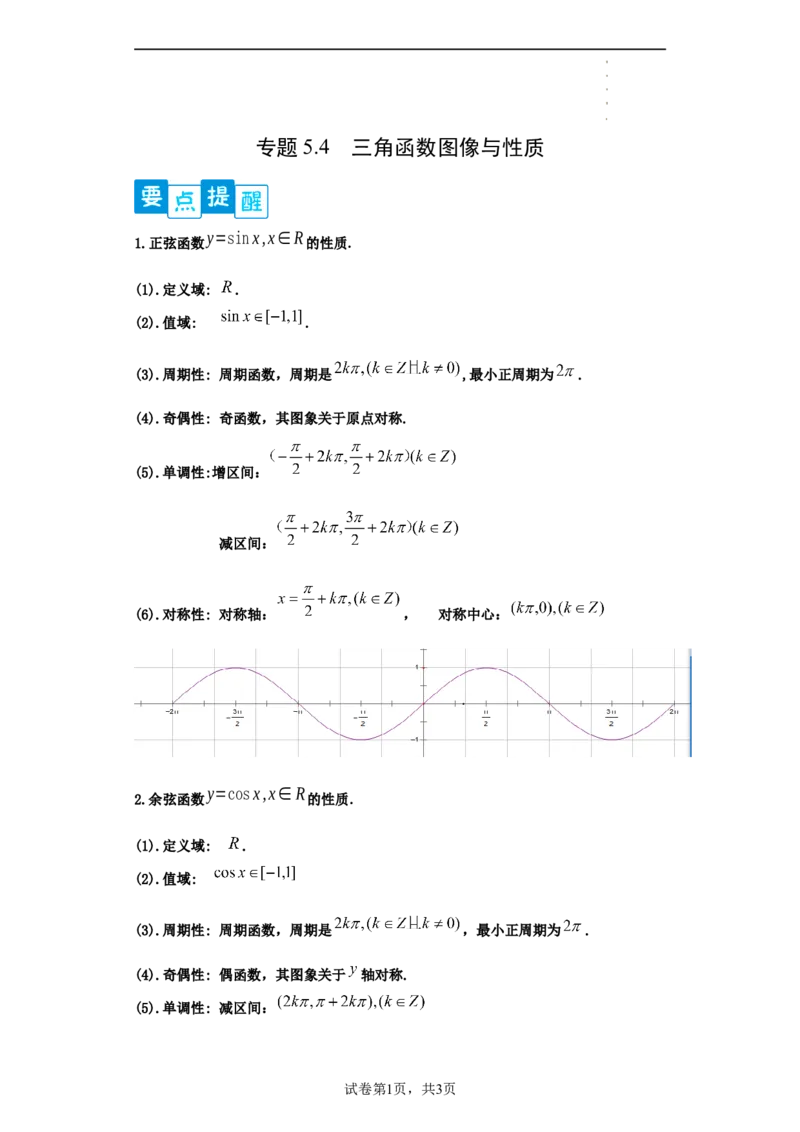
1.正弦函数 的性质.
(1).定义域: .
(2).值域: .
(3).周期性: 周期函数,周期是 ,最小正周期为 .
(4).奇偶性: 奇函数,其图象关于原点对称.
(5).单调性:增区间:
减区间:
(6).对称性: 对称轴: , 对称中心:
y=cosx,x∈R
2.余弦函数 的性质.
(1).定义域: .
(2).值域:
(3).周期性: 周期函数,周期是 ,最小正周期为 .
(4).奇偶性: 偶函数,其图象关于 轴对称.
(5).单调性: 减区间:
试卷第1页,共3页
学科网(北京)股份有限公司增区间:
(6).对称性: 对称轴: , 对称中心:
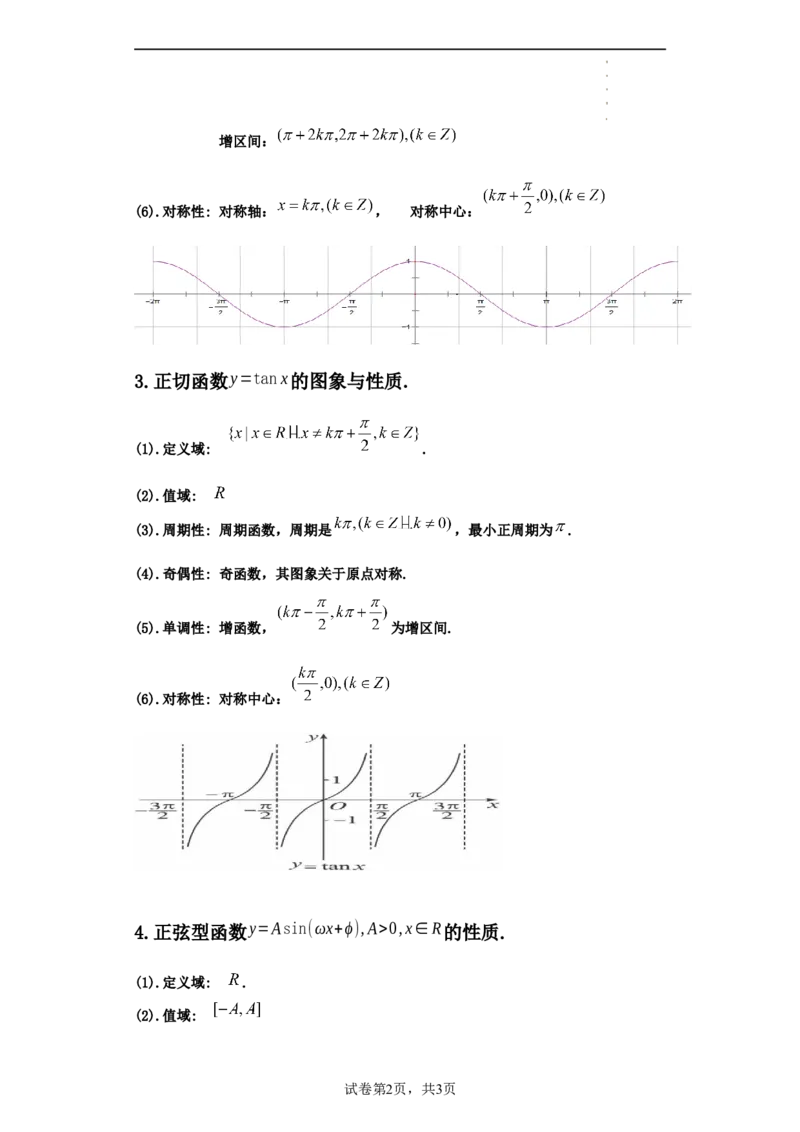
3.正切函数y=tanx的图象与性质.
(1).定义域: .
(2).值域:
(3).周期性: 周期函数,周期是 ,最小正周期为 .
(4).奇偶性: 奇函数,其图象关于原点对称.
(5).单调性: 增函数, 为增区间.
(6).对称性: 对称中心:
4.正弦型函数y=Asin(ωx+ϕ),A>0,x∈R的性质.
(1).定义域: .
(2).值域:
试卷第2页,共3页
学科网(北京)股份有限公司(3).周期性: 周期函数,周期是 .
(4).奇偶性: 当 时为奇函数;当 时为偶函数.
(5).单调性: 当 时:令 ,求解增区间.
令 ,求解减区间.
当 时:注意单调区间的转化 .
(6).对称性: 对称轴:令 ,求解对称轴方程,对称轴处取最
值.
对称中心:令 ,求解对称中心坐标.
5.余弦型函数y=Acos(ωx+ϕ),A>0,x∈R的性质.
(1).定义域: .
(2).值域:
(3).周期性: 周期函数,周期是 .
(4).奇偶性: 当 时为偶函数;当 时为奇函数.
(5).单调性: 当 时:令 ,求解减区间.
令 ,求解增区间.
当 时:注意单调区间的转化 .
(6).对称性: 对称轴:令 ,求解对称轴方程,对称轴处取最值.
试卷第3页,共3页
学科网(北京)股份有限公司对称中心:令 ,求解对称中心坐标.
一、单选题
1.已知函数 ,则( )
A. 的最小正周期为 ,对称中心为
B. 的最小正周期为 ,对称中心为
C. 的最小正周期为 ,对称中心为
D. 的最小正周期为 ,对称中心为
2.用“五点法”作函数 在一个周期内的图像时,第四个关键点的坐标
是
A. B.
C. D.
试卷第4页,共3页
学科网(北京)股份有限公司3.若函数 在区间 内没有最值,则 的取值范围是
( )
A. B.
C. D.
4.已知函数 在区间 内单调递减,则实数ω的取值范
围是( )
A. B. C. D.
5.已知 是 上的奇函数,若 的图象关于直线
对称,且 在区间 内是单调函数,则 ( )
A. B. C. D.
6.函数 的值域为( )
A. B.
C. D.
试卷第5页,共3页
学科网(北京)股份有限公司7.已知 且 ,则 的取值范围为( )
A. B.
C. D.
8.已知函数 在 上单调递增,则 的值可以是( )
A. B. C. D.
9.函数 的一个单调递减区间是( )
A. B. C. D.
10.已知函数 在 上有且只有4个零点,则 取值范围
是( )
A. B. C. D.
11.函数 的定义域是( )
A. B.
试卷第6页,共3页
学科网(北京)股份有限公司C. D.
12.函数 的单调减区间是( )
A. B.
C. D.
13.已知函数 为偶函数,则 的取值可以为( )
A. B. C. D.0
14.记函数 ( )的最小正周期为 .若 ,且
的图象关于点 中心对称,则 ( )
A.1 B. C. D.3
15.已知函数 的最大值为4,最小值为0,且
该函数图象的相邻两个对称轴之间的最短距离为 ,直线 是该函数图象的一条
对称轴,则该函数的解析式是( )
A. B.
试卷第7页,共3页
学科网(北京)股份有限公司C. D.
二、多选题
16.已知函数 ,则下列说法正确的是( )
A. 在定义域内是增函数 B. 是奇函数
C. 的最小正周期是 D. 图像的对称中心是
17.已知 为 上的奇函数,且当 时, ,记
,下列结论正确的是( )
A. 为奇函数
B.若 的一个零点为 ,且 ,则
C. 在区间 的零点个数为3个
D.若 大于1的零点从小到大依次为 ,则
18.已知函数 ,点 和 是其相邻的两个
对称中心,且在区间 内单调递减,则 ( )
试卷第8页,共3页
学科网(北京)股份有限公司A. B. C. D.
19.设函数 ,若 在 上有且仅有3条对称轴,则
( )
A. 在 上有且仅有2个最大值点
B. 在 上有且仅有2个零点
C. 的取值范围是
D. 在 上单调递增
20.已知函数 ,则下列命题正确的是( )
A.若 在 上有10个零点,则
B.若 在 上有11条对称轴,则
C.若 = 在 上有12个解,则
D.若 在 上单调递减,则
21.函数 ,对于任意的 ,方程
试卷第9页,共3页
学科网(北京)股份有限公司仅有一个实数根,则m的取值可以为( )
A. B. C. D.
22.已知函数 ,则下列关于 的判断正确的是( )
A.在区间 上单调递增 B.最小正周期是
C.图象关于直线 成轴对称 D.图象关于点 成中心对称
三、解答题
23.已知
(1)函数 ( )在区间 上恰有三条对称轴,求 的取值范围.
(2)函数 ,
①当 时,求函数 (x)的零点;
②当 ,恒有 ,求实数 的取值范围.
24.已知函数 ,图象上任意两条相邻对称轴间的距离为 .
(1)求函数的单调区间和对称中心.
(2)若关于 的方程 在 上有实数解,求实数 的取值范
围.
25.已知函数 .
(1)请用五点法做出 一个周期内的图像;
试卷第10页,共3页
学科网(北京)股份有限公司(2)若函数 在区间 上有两个零点,请写出 的取值范围,无需说明
理由.
26.已知函数 , )函数关于 对称.
(1)求 的解析式;
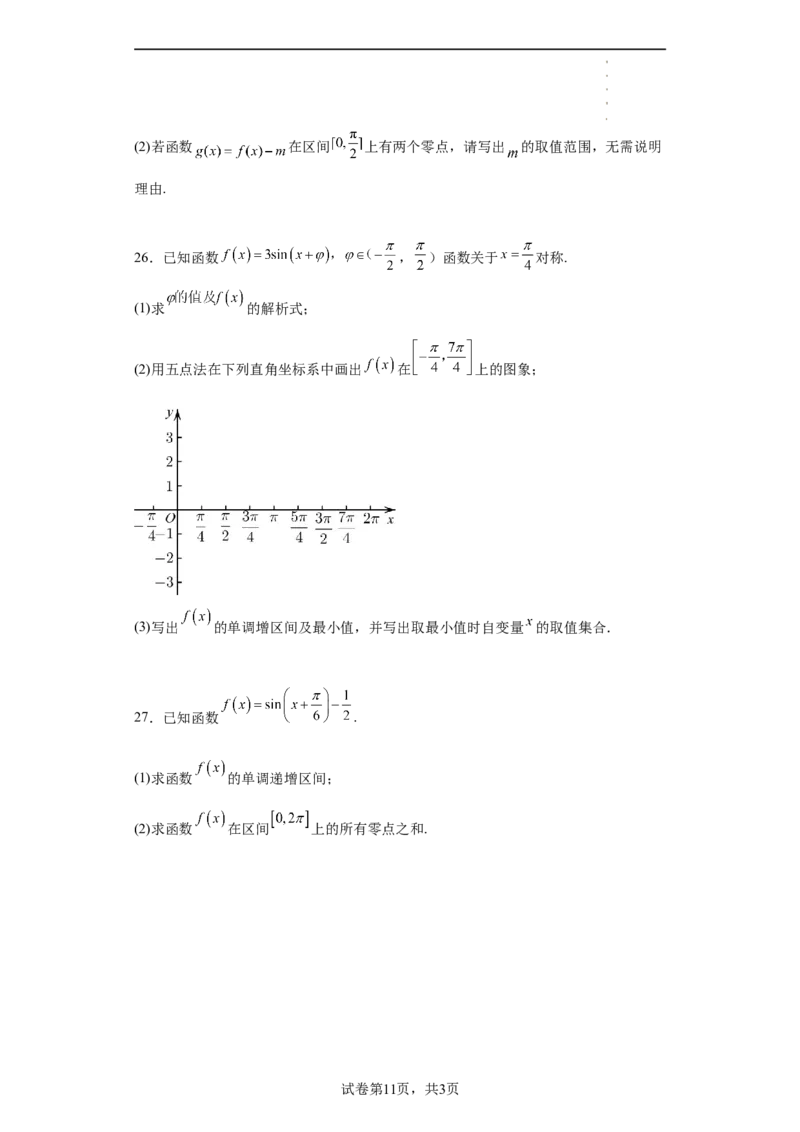
(2)用五点法在下列直角坐标系中画出 在 上的图象;
(3)写出 的单调增区间及最小值,并写出取最小值时自变量 的取值集合.
27.已知函数 .
(1)求函数 的单调递增区间;
(2)求函数 在区间 上的所有零点之和.
试卷第11页,共3页
学科网(北京)股份有限公司试卷第12页,共3页
学科网(北京)股份有限公司