文档内容
专题 5.6 函数y=Asin(ωx+φ)的图像和性质
1 性质
(1) 简谐运动可用函数y=Asin(ωx+φ),x∈[0,+∞)表示,
2π 1 ω
A是振幅,周期T= ,频率 f = = ,相位ωx+φ ,初相φ.
ω T 2π
(2) A,ω,φ对f(x)=Asin(ωx+φ)的影响
A影响函数y=f(x)的最值,ω影响周期,φ影响函数水平位置.
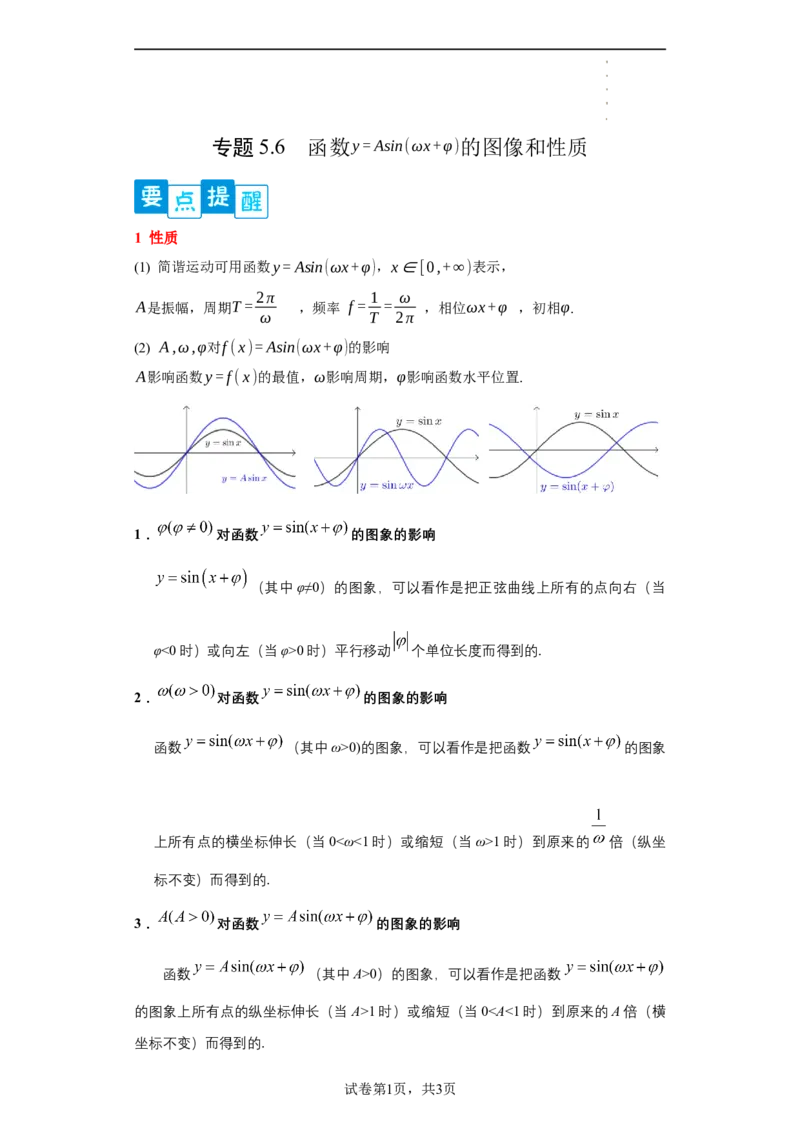
1. 对函数 的图象的影响
(其中φ≠0)的图象,可以看作是把正弦曲线上所有的点向右(当
φ<0时)或向左(当φ>0时)平行移动 个单位长度而得到的.
2. 对函数 的图象的影响
函数 (其中ω>0)的图象,可以看作是把函数 的图象
上所有点的横坐标伸长(当0<ω<1时)或缩短(当ω>1时)到原来的 倍(纵坐
标不变)而得到的.
3. 对函数 的图象的影响
函数 (其中A>0)的图象,可以看作是把函数
的图象上所有点的纵坐标伸长(当A>1时)或缩短(当00)将y=f(x)图像沿x轴向左(右)平移a个单位(左加右
减);
② y=f (x)⟶y=f (x)± b (b>0)将y=f(x)图像沿x轴向上(下)平移b个单位(上加
下减).
π π
PS f(x)=3sin(2x+ )向 左 平 移 个 单 位 , 得 到 的 函 数 不 是
3 4
π π π π
f(x)=3sin(2x+ + ), 而是f(x)=3sin[2(x+ )+ ].
4 3 4 3
(2) 伸缩变换
① y=f (x)⟶ y=A f (x)(A>0)
将y=f(x)图像横坐标不变,纵坐标伸长到原来的A倍(A>1伸长,A<1缩短).
② y=f (x)⟶ y=f (ω x)(ω>0)
1
将y=f(x)图像纵坐标不变,横坐标缩到原来的 倍( ω>1缩短,ω<1伸长);
ω
( π)
问题 怎么理解呢?例:若将f (x)=3sin x+ 图像纵坐标不变,横坐标缩到原来的
3
1 ( π) (1 π)
倍,那得到的函数是f (x)=3sin 2x+ 还是f (x)=3sin x+ 呢?
2 3 2 3
( π)
解析 我们把f (x)=3sin x+ 的图象想象成一条弹簧,若纵坐标不变,横坐标缩到
3
1 2π
原来的 倍,那说明弹簧被压缩了,则周期变小,ω会变大(T= ,T与ω成反比),
2 ω
( π)
即变换后的函数应该是f (x)=3sin 2x+ .
3
试卷第2页,共3页
学科网(北京)股份有限公司图像平移变换
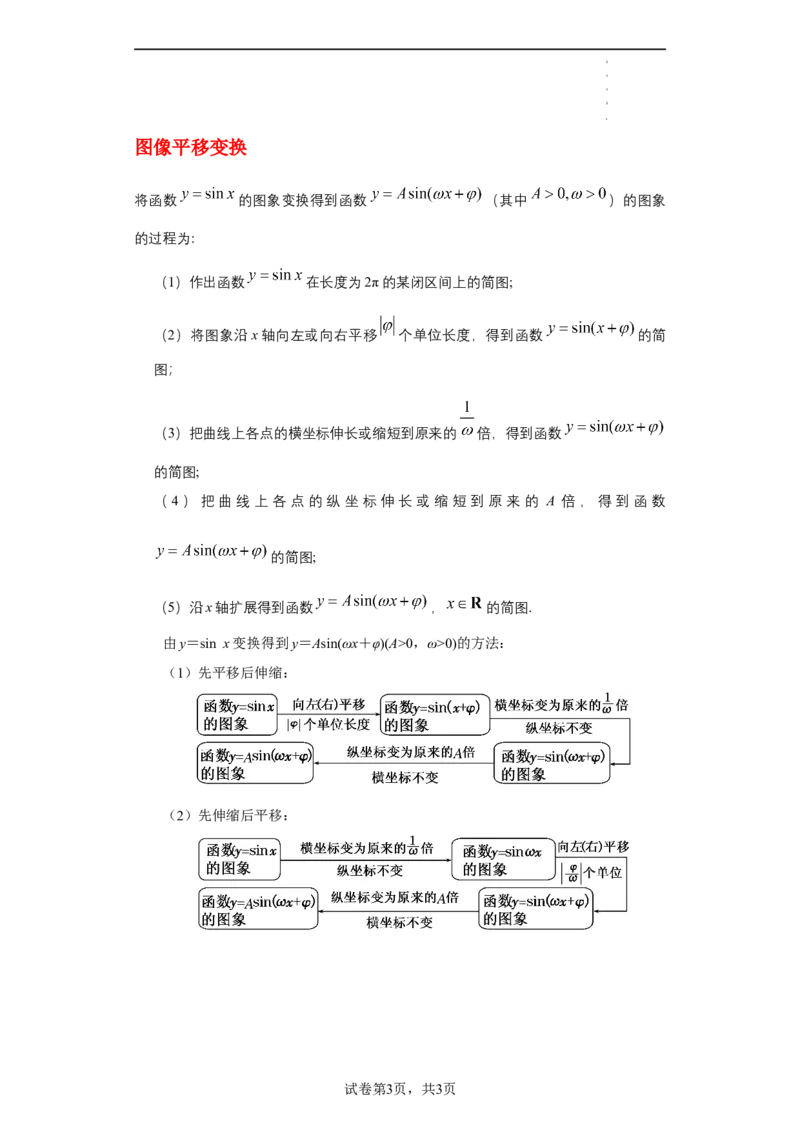
将函数 的图象变换得到函数 (其中 )的图象
的过程为:
(1)作出函数 在长度为2π的某闭区间上的简图;
(2)将图象沿x轴向左或向右平移 个单位长度,得到函数 的简
图;
(3)把曲线上各点的横坐标伸长或缩短到原来的 倍,得到函数
的简图;
(4)把曲线上各点的纵坐标伸长或缩短到原来的 A 倍,得到函数
的简图;
(5)沿x轴扩展得到函数 , 的简图.
由y=sin x变换得到y=Asin(ωx+φ)(A>0,ω>0)的方法:
(1)先平移后伸缩:
(2)先伸缩后平移:
试卷第3页,共3页
学科网(北京)股份有限公司一、单选题
1.已知函数 ,则函数 的图象可以由 的图象( )
A.向左平移 得到 B.向右平移 得到
C.向左平移 得到 D.向右平移 得到
【来源】陕西省宝鸡市陈仓区2021-2022学年高一下学期期末数学试题
【答案】A
【解析】由题意,由 的图象向左平移 得到函数 故选:A
2.将函数 图象上所有点的横坐标伸长到原来的2倍,纵坐标不变,
所得图象的函数表达式为( )
A. B.
C. D.
【来源】辽宁省丹东市2021-2022学年高一下学期期末数学试题
【答案】C
【解析】:将函数 图象上所有点的横坐标伸长到原来的2倍,纵坐
标不变,得到 .故选:C
3.将函数 的图象向左平移 个单位长度后,所得到的图象关于
试卷第4页,共3页
学科网(北京)股份有限公司轴对称,则 的最小值是( )
A. B. C. D.
【来源】陕西省宝鸡市渭滨区2021-2022学年高一下学期期末数学试题
【答案】B
【解析】因为函数 的图象向左平移 个单位长度后,所得函数
解析式为 ;
由函数 的图象关于 轴对称,所以 ,
即 ,因为 ,所以当 时, 取到最小值 .故选:B.
4.为了得到函数 的图像,需对函数 的图像所作的变换
可以为( )
A.先将图像上所有的横坐标伸长为原来的3倍,纵坐标不变,再向左平移 个单位
B.先将图像上所有的横坐标缩短为原来的 ,纵坐标不变,再向右平移 个单位
C.先将图像上所有的横坐标缩短为原来的 ,纵坐标不变,再向左平移 个单位
D.先将图像上所有的横坐标伸长为原来的3倍,纵坐标不变,再向右平移 个单位
【来源】上海市吴淞中学2021-2022学年高一下学期期末数学试题
【答案】B
【解析】对于A,先将 的图像上所有的横坐标伸长为原来的3倍,纵坐标
不变,再向左平移 个单位,所得图像的解析式为 ,
故A错误;
试卷第5页,共3页
学科网(北京)股份有限公司对于B,先将 的图像上所有的横坐标缩短为原来的 ,纵坐标不变,再向
右平移 个单位,所得图像的解析式为 ,故B正确;
对于C,先将 的图像上所有的横坐标缩短为原来的 ,纵坐标不变,再向
左平移 个单位,所得图像的解析式为 ,故C错误;
对于D,先将 的图像上所有的横坐标伸长为原来的3倍,纵坐标不变,再
向右平移 个单位,所得图像的解析式为 ,故D错
误;故选:B.
5.要得到函数 的图象,只需将函数 的图象( )
A.向左平移 个单位 B.向右平移 个单位
C.向左平移 个单位 D.向右平移 个单位
【来源】四川省巴中市2021-2022学年高一下学期期末数学理科试题
【答案】D
【解析】:
要得到函数 的图象,只需将函数 的图象向右平移 个单位即
可,即 .故选:D.
试卷第6页,共3页
学科网(北京)股份有限公司6.已知函数 的最小正周期为 ,将 的图象向左平移 个
单位长度,再把得到的曲线上各点的横坐标伸长到原来的2倍,得到函数 的图象,
则下列结论不正确的是( )
A. B. 的图象关于点 对称
C. 的图象关于 对称 D. 在 上的最大值是1
【来源】湖北省随州市曾都区第一中学2021-2022学年高一下学期期末模拟数学试题
【答案】D
【解析】因为 ,所以 , .
将 的图象向左平移 个单位长度,得到 ,
再把得到的曲线上各点的横坐标伸长到原来的2倍,得到 .
对选项A, ,故A正确.
对选项B, ,所以 的图象关于点 对称,故B正确.
对选项C, ,所以 的图象关于 对称.故C正确.
对选项D, , ,所以 ,
所以 ,故 在 上的最大值是 ,故D错误.
故选:D
7.关于函数 有如下四个命题:
试卷第7页,共3页
学科网(北京)股份有限公司甲:该函数在 上单调递减;
乙:该函数图象向左平移 个单位长度得到一个偶函数;
丙:该函数图象的一条对称轴方程为
丁:该函数图象的一个对称中心为 .
如果只有一个假命题.则该命题是( )
A.甲 B.乙 C.丙 D.丁
【答案】C
【解析】设 ,
若丙丁都正确,则 且 ,
但 ,故矛盾,
所以丙丁中有一个是错误的,故甲乙都正确,
函数 的图象向左平移 个单位长度后所得图象对应的解析式为:
,
因为平移后的图象对应的函数为偶函数,故 ,
故 ,
若 为偶数,则 ,
当 , ,
因为 在 为减函数,故 在 为减函数,符合,
试卷第8页,共3页
学科网(北京)股份有限公司若 为奇数,则 ,
当 , ,
因为 在 为减函数,故 在 为增函数,舍,
故 .
而 ,故该函数图象的对称中心为 ,丙错误,
,故该函数图象的对称中心为 ,丁正确.
故选:C
8.若将函数 的图像先向左平移 个单位长度,然后再保持纵坐标
不变,横坐标伸长为原来的2倍,得到 的图像,则( )
A. B.
C. D.
【来源】重庆市第一中学校2021-2022学年高一下学期期中数学试题
【答案】A
【解析】将函数 的图像先向左平移 个单位长度,
得 ,
试卷第9页,共3页
学科网(北京)股份有限公司再将横坐标伸长为原来的2倍,得 ,
所以函数 的解析式为 .故选:A
9.将 图象上每一个点的横坐标变为原来的3倍(纵坐标不变),得到
的图象,再将 图象向左平移 ,得到 的图象,则
的解析式为( )
A. B. C. D.
【来源】江苏省南通市如皋中学2021-2022学年高一上学期期末数学试题
【答案】A
【解析】将 图象上每一个点的横坐标变为原来的3倍(纵坐标不变),
得到 的图象,
再将 图象向左平移 ,得到 的图象,故选:
A.
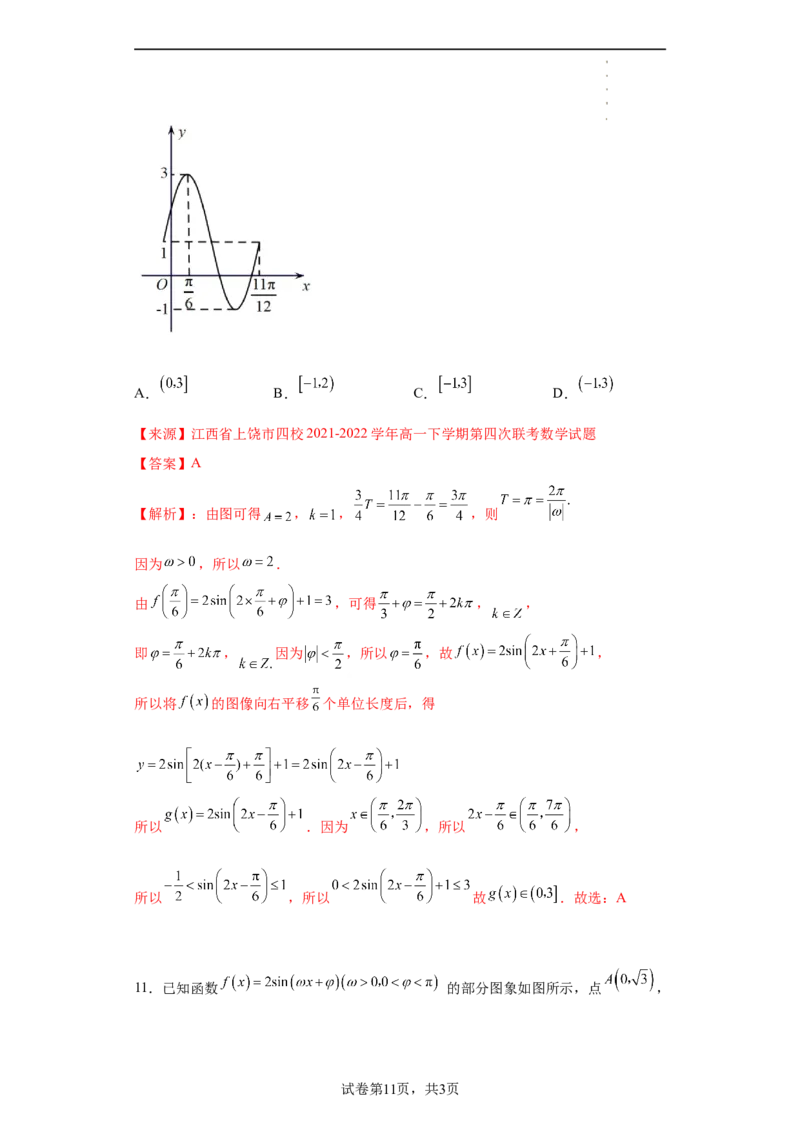
10.已知函数 的部分图像如图所示,将
的图像向右平移 个单位长度后,得到函数 的图像,则 在 上
的值域为( )
试卷第10页,共3页
学科网(北京)股份有限公司A. B. C. D.
【来源】江西省上饶市四校2021-2022学年高一下学期第四次联考数学试题
【答案】A
【解析】:由图可得 , , ,则
因为 ,所以 .
由 ,可得 , ,
即 , 因为 ,所以 ,故 ,
所以将 的图像向右平移 个单位长度后,得
所以 .因为 ,所以 ,
所以 ,所以 故 .故选:A
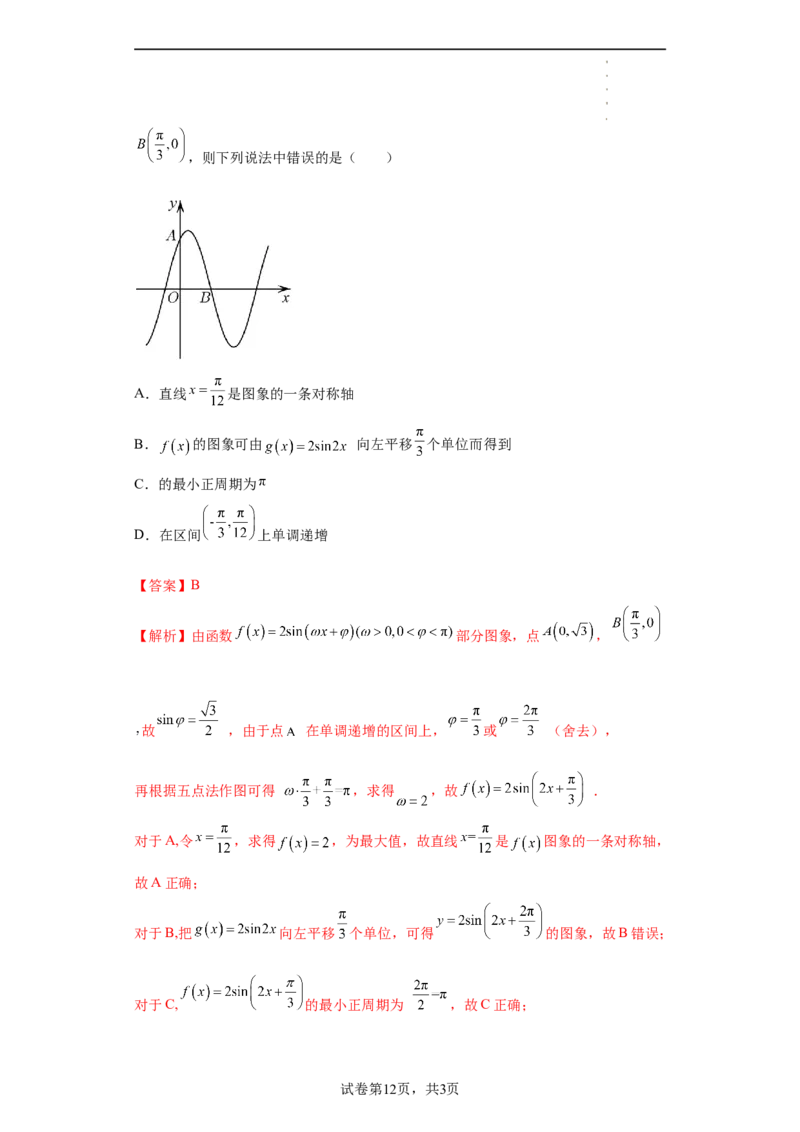
11.已知函数 的部分图象如图所示,点 ,
试卷第11页,共3页
学科网(北京)股份有限公司,则下列说法中错误的是( )
A.直线 是图象的一条对称轴
B. 的图象可由 向左平移 个单位而得到
C.的最小正周期为
D.在区间 上单调递增
【答案】B
【解析】由函数 部分图象,点 ,
故 ,由于点 在单调递增的区间上, 或 (舍去),
再根据五点法作图可得 ,求得 ,故 .
对于A,令 ,求得 ,为最大值,故直线 是 图象的一条对称轴,
故A正确;
对于B,把 向左平移 个单位,可得 的图象,故B错误;
对于C, 的最小正周期为 ,故C正确;
试卷第12页,共3页
学科网(北京)股份有限公司对于D, , ,故 单调递增,故D对.
故选:B
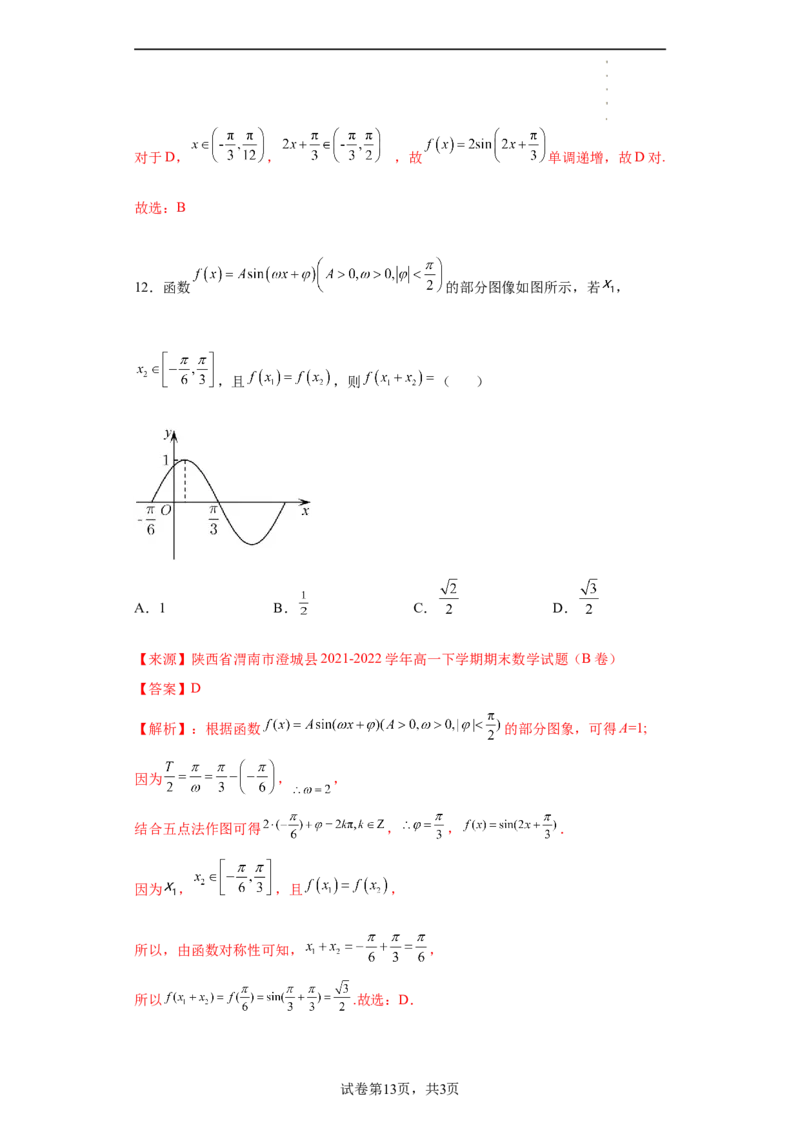
12.函数 的部分图像如图所示,若 ,
,且 ,则 ( )
A.1 B. C. D.
【来源】陕西省渭南市澄城县2021-2022学年高一下学期期末数学试题(B卷)
【答案】D
【解析】:根据函数 的部分图象,可得A=1;
因为 , ,
结合五点法作图可得 , , .
因为 , ,且 ,
所以,由函数对称性可知, ,
所以 .故选:D.
试卷第13页,共3页
学科网(北京)股份有限公司13.已知函数 (其中 , , )的部分图象如图所
示,则下列结论不正确的是( )
A.函数 的图象关于点 对称
B.
C.函数 的图象关于直线 对称
D.函数 在区间 上单调递增
【来源】河南省濮阳市2021-2022学年高一下学期期末数学(理科)试题
【答案】C
【解析】由图象可得:A=2,最小正周期为 ,所以 ,
又
又 ,所以 ,所以 .
对于A, ,
所以 是f(x)的一个对称中心,故A正确;
试卷第14页,共3页
学科网(北京)股份有限公司对于B, ,故B正确;
对于C, ,故C不正确;
对于D,令 ,
解得: ,令 ,
所以D正确.故选:C.
14.将函数 的图象向左平移 个单位,得到函数
的图象,若 在 上为增函数,则 的最大值为( )
A.1 B.2 C.3 D.4
【来源】广西柳州市2021-2022学年高一下学期期末联考数学试题
【答案】A
【解析】函数 的图象向左平移 个单位,
得到函数 ,
若 ,则 ,所以 ,即 ,
所以 的最大值为1.故选:A.
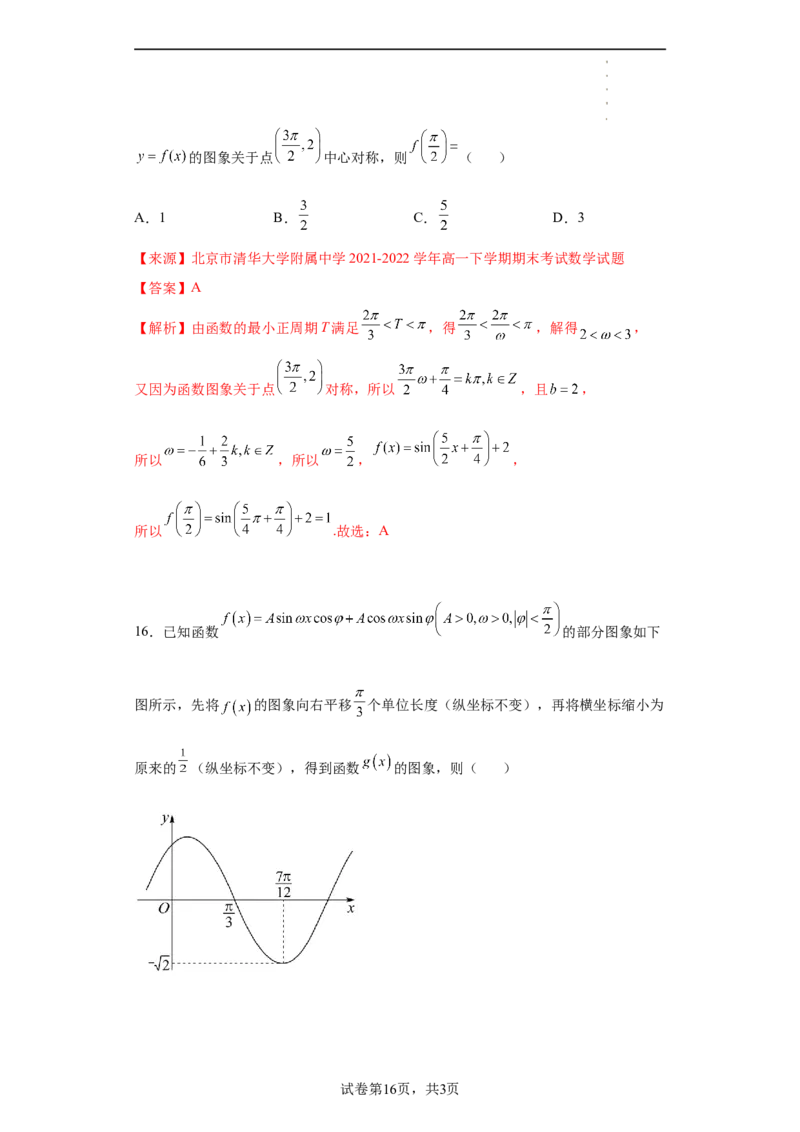
15.记函数 的最小正周期为T.若 ,且
试卷第15页,共3页
学科网(北京)股份有限公司的图象关于点 中心对称,则 ( )
A.1 B. C. D.3
【来源】北京市清华大学附属中学2021-2022学年高一下学期期末考试数学试题
【答案】A
【解析】由函数的最小正周期T满足 ,得 ,解得 ,
又因为函数图象关于点 对称,所以 ,且 ,
所以 ,所以 , ,
所以 .故选:A
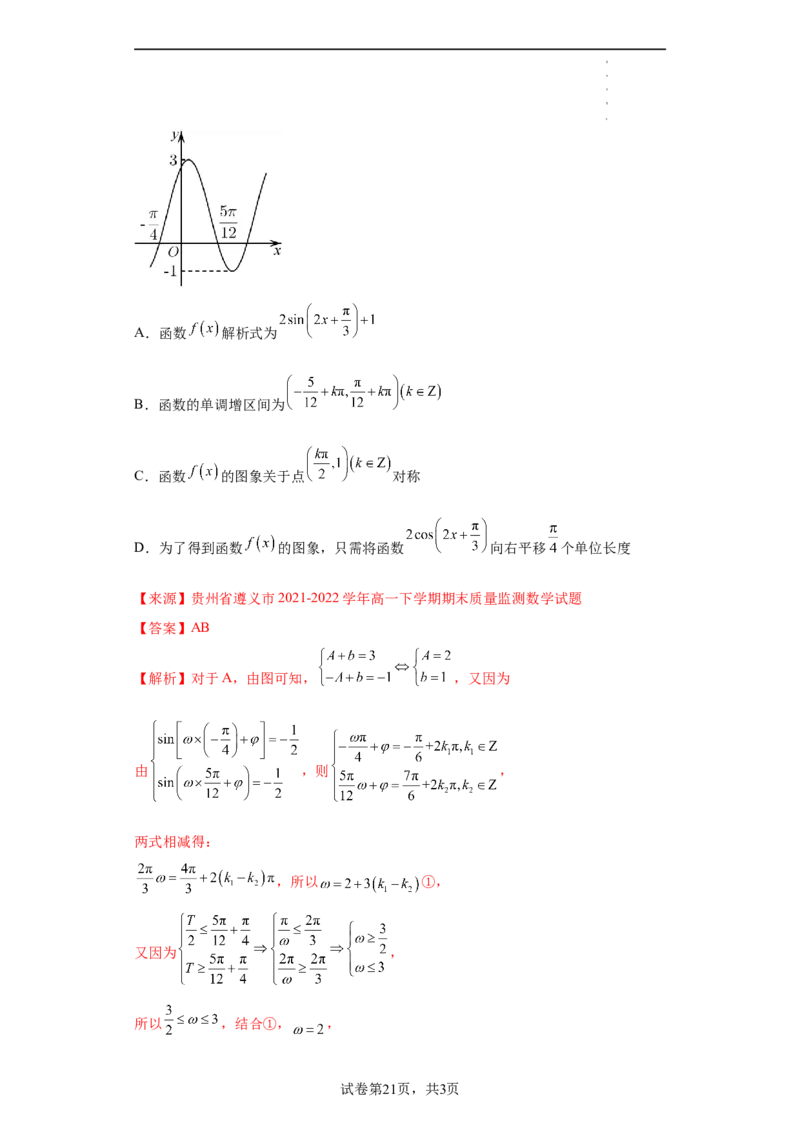
16.已知函数 的部分图象如下
图所示,先将 的图象向右平移 个单位长度(纵坐标不变),再将横坐标缩小为
原来的 (纵坐标不变),得到函数 的图象,则( )
试卷第16页,共3页
学科网(北京)股份有限公司A. B.
C. D.
【来源】江西省名校2021-2022学年高一下学期期中调研数学试题
【答案】D
【解析】 ,由图知周期
,
解得 ,又最小值为 ,所以 ,故 .
又 ,结合 ,可得 ,
所以 .
将 的图象向右平移 个单位长度(纵坐标不变),
得到 ,再将横坐标缩小为原来的 ,
得到
故选:D.
17.将函数 的图象向左平移 个单位,得到函数
的图象,若函数 在区间 上单调递增,则 的值可能为( )
A. B. C.3 D.4
试卷第17页,共3页
学科网(北京)股份有限公司【来源】辽宁省大连市第一〇三中学2021-2022学年高一下学期期中考试数学试题
【答案】B
【解析】:将函数 的图象向左平移 个单位,
得到函数 ,
因为 ,所以 ,
又因为函数 在区间 上单调递增,
所以 ,解得,
所以 的值可能为 ,故选:B
18.函数 在区间 上单调且 ,则 的范围
是( )
A. B. C. D.
【来源】广东省十五校联盟2021-2022学年高一下学期第一次联考数学试题
【答案】A
【解析】因为函数 在区间 上单调且 ,又
,
所以 ,且 ,解得 .
故选: A.
试卷第18页,共3页
学科网(北京)股份有限公司19.将函数 向右平移 个单位长度得到函数 ,若函数
在 上的值域为 ,则实数 的取值范围是( )
A. B. C. D.
【来源】安徽省淮北一中、安师大附中、铜陵一中、中科大附中四校2021-2022学年
高一下学期学业水平调研数学试题
【答案】B
【解析】将函数 向右平移 个单位长度得到函数
,
由 ,得 ,
由 ,得 ,
所以 ,
所以 ,
故选:B.
20.已知函数 在区间 上单调递
增,且在区间 上只取得一次最大值,则 的取值范围是( )
A. B. C. D.
试卷第19页,共3页
学科网(北京)股份有限公司【来源】天津市部分区2021-2022学年高一上学期期末数学试题
【答案】C
【解析】因为
,
因为 在区间 上单调递增,由 ,则
,
则 ,解得 ,即 ;
当 时, ,要使得该函数取得一次最大值,
故只需 ,解得 ;
综上所述, 的取值范围为 .
故选:C.
二、多选题
21.函数 ,( , )部分图象如图所示,下列说法正
确的是( )
试卷第20页,共3页
学科网(北京)股份有限公司A.函数 解析式为
B.函数的单调增区间为
C.函数 的图象关于点 对称
D.为了得到函数 的图象,只需将函数 向右平移 个单位长度
【来源】贵州省遵义市2021-2022学年高一下学期期末质量监测数学试题
【答案】AB
【解析】对于A,由图可知, ,又因为
由 ,则 ,
两式相减得:
,所以 ①,
又因为 ,
所以 ,结合①, ,
试卷第21页,共3页
学科网(北京)股份有限公司因为 ,所以
所以 ,故A正确;
对于B, ,
解得: ,故B正确;
对于C,令 ,解得: ,
函数 的图象关于点 对称,所以C不正确;
对于D,将函数 向右平移 个单位得到
,故D不正确.
故选:AB.
22.设函数 ,则( )
A. 为奇函数
B. 的图象关于直线 对称
C.当 时, 的最小值为
D.将 的图象向右平移 个单位,可以得到函数 的图象
【来源】辽宁省丹东市2021-2022学年高一下学期期末数学试题
【答案】ACD
试卷第22页,共3页
学科网(北京)股份有限公司【解析】对于A, , ,
为奇函数,A正确;
对于B,当 时, ,
不是 的对称轴, 的图象不关于直线 对称,B错误;
对于C, , 当 时, 分别取得 的最
大值和最小值,
,C正确;
对于D, 的图象向右平移 个单位可得:
,即得到 的图象,D
正确.故选:ACD.
23.已知 的图象关于点 对称,相邻两条对称
轴的距离为 ,则下列说法正确的是( )
A. ,
B.将函数 的图象向右平移 个单位长度后,得到的图象关于y轴对称
C.函数 在 上的单调递减区间为
试卷第23页,共3页
学科网(北京)股份有限公司D.为了得到 的图象,可以将函数 的图象向右平移 个单位
【来源】贵州省黔东南州2021-2022学年高一下学期期末文化水平测试数学试题
【答案】BC
【解析】:因为相邻两条对称轴的距离为 ,故周期为 ,则 ,
图象关于点 对称,则 ,因为 ,所以 ,A错;
,
将函数 的图象向右平移 个单位长度后得 ,该函数是偶函
数,图象关于y轴对称,B正确;
令 ,得 ,
所以函数 在 上的单调递减区间为 ,C正确;
为了得到 的图象,应该将函数 的图象向右平移 个单位,D错.
故选:BC.
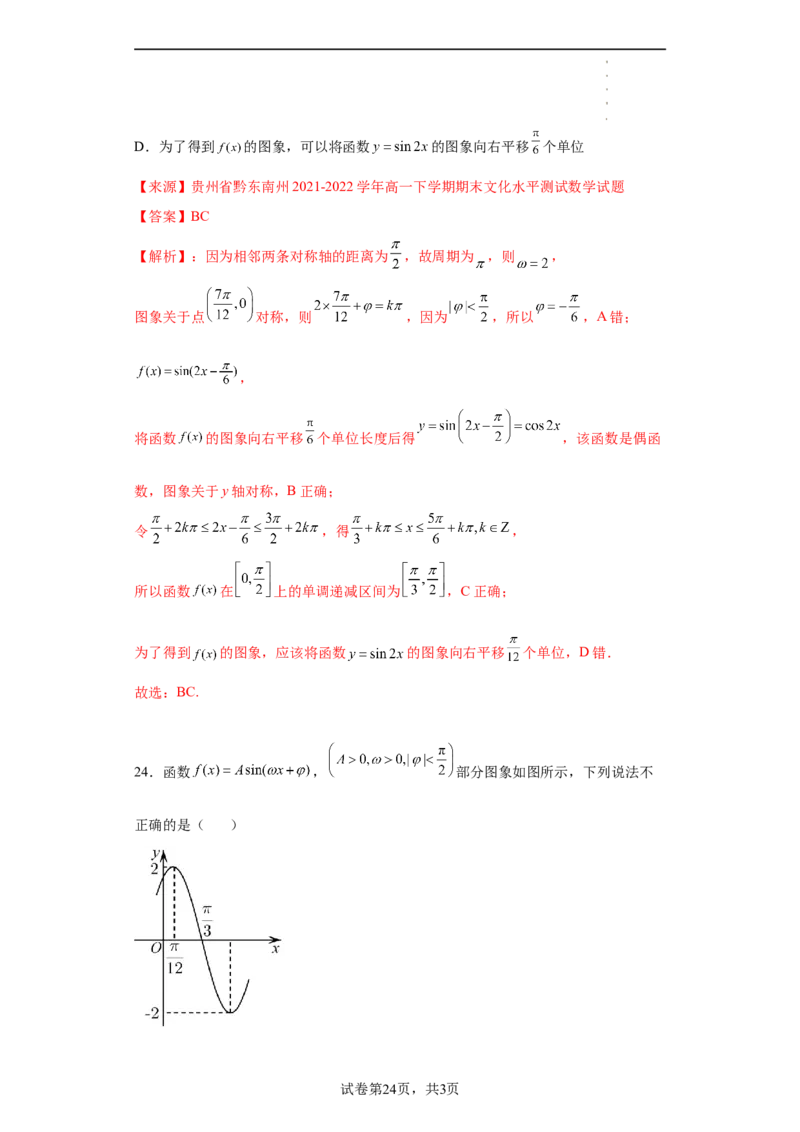
24.函数 , 部分图象如图所示,下列说法不
正确的是( )
试卷第24页,共3页
学科网(北京)股份有限公司A. 的图象关于直线 对称
B. 的图象关于点 对称
C.将函数 的图象向左平移 个单位得到函数 的图象
D.若方程 在 上有两个不相等的实数根,则m的取值范围是
【来源】黑龙江省双鸭山市第一中学2021-2022学年高一下学期期中考试数学试题
【答案】AC
【解析】从图象可以看出, , ,
因为 ,所以 ,
解得: ,将 代入解析式, ,
其中 ,解得: ,所以 ,
当 时, ,
故 不是 的对称轴,A错误;
从图象可以看出 的图象关于点 对称,B正确;
的图象向左平移 个单位后得到
,故C错误;
,则 ,
试卷第25页,共3页
学科网(北京)股份有限公司值域为 ,且在 上单调递减,在 上单调递
增,画出函数y=2sinx对应图象如下:
显然方程 在 上有两个不相等的实数根,则m的取值范围是 ,
D正确;故选:AC
25.将函数 的图象向左平移 ( )个单位,得到函数 的图象,
若函数 是奇函数,则 的可能取值为( )
A. B. C. D.
【来源】吉林省长春市十一高中2021-2022学年高一上学期期末数学试题
【答案】AC
【解析】将函数 的图象向左平移 ( )个单位,
得到函数 ,
因为函数 是奇函数,
所以 ,
解得 ,
所以 的可能取值为 , ,故选:AC
三、填空题
试卷第26页,共3页
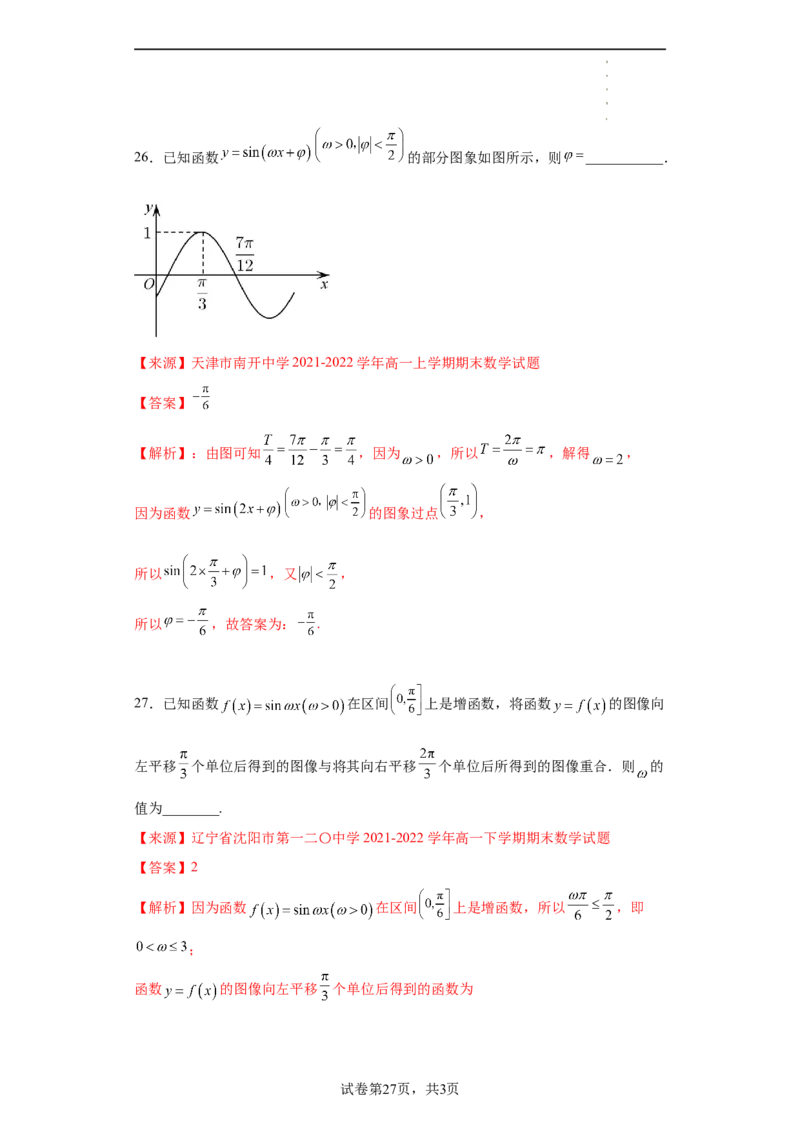
学科网(北京)股份有限公司26.已知函数 的部分图象如图所示,则 ___________.
【来源】天津市南开中学2021-2022学年高一上学期期末数学试题
【答案】
【解析】:由图可知 ,因为 ,所以 ,解得 ,
因为函数 的图象过点 ,
所以 ,又 ,
所以 ,故答案为: .
27.已知函数 在区间 上是增函数,将函数 的图像向
左平移 个单位后得到的图像与将其向右平移 个单位后所得到的图像重合.则 的
值为________.
【来源】辽宁省沈阳市第一二〇中学2021-2022学年高一下学期期末数学试题
【答案】2
【解析】因为函数 在区间 上是增函数,所以 ,即
;
函数 的图像向左平移 个单位后得到的函数为
试卷第27页,共3页
学科网(北京)股份有限公司,
函数 的图像向右平移 个单位后所得到的函数为
;
因为二者的图像重合,所以 , ,即 .
所以 .
故答案为:2.
28.已知函数 的部分图象如图所示,将该函数的图象向左平移t(
)个单位长度,得到函数 的图象.若函数 的图象关于原点对称,
则t的最小值为________.
【来源】湖南省长沙市第一中学2021-2022学年高一下学期期末数学试题
【答案】
【解析】:由图象可得 时,函数 的函数值为0,即
,
,
试卷第28页,共3页
学科网(北京)股份有限公司,将此函数向左平移 个单位得, ,
又 为奇函数,
, ,
的最小值是 .故答案为: .
29.设函数 若 在区间 上单调,且
,则 的最小正周期为____.
【答案】
【解析】函数 , , ,若 在区间 上单调,
则 , .
, 为 的一条对称轴,
且 即 为 的一个对称中心,
只有当 时,解得 , ,
故答案为:
四、解答题
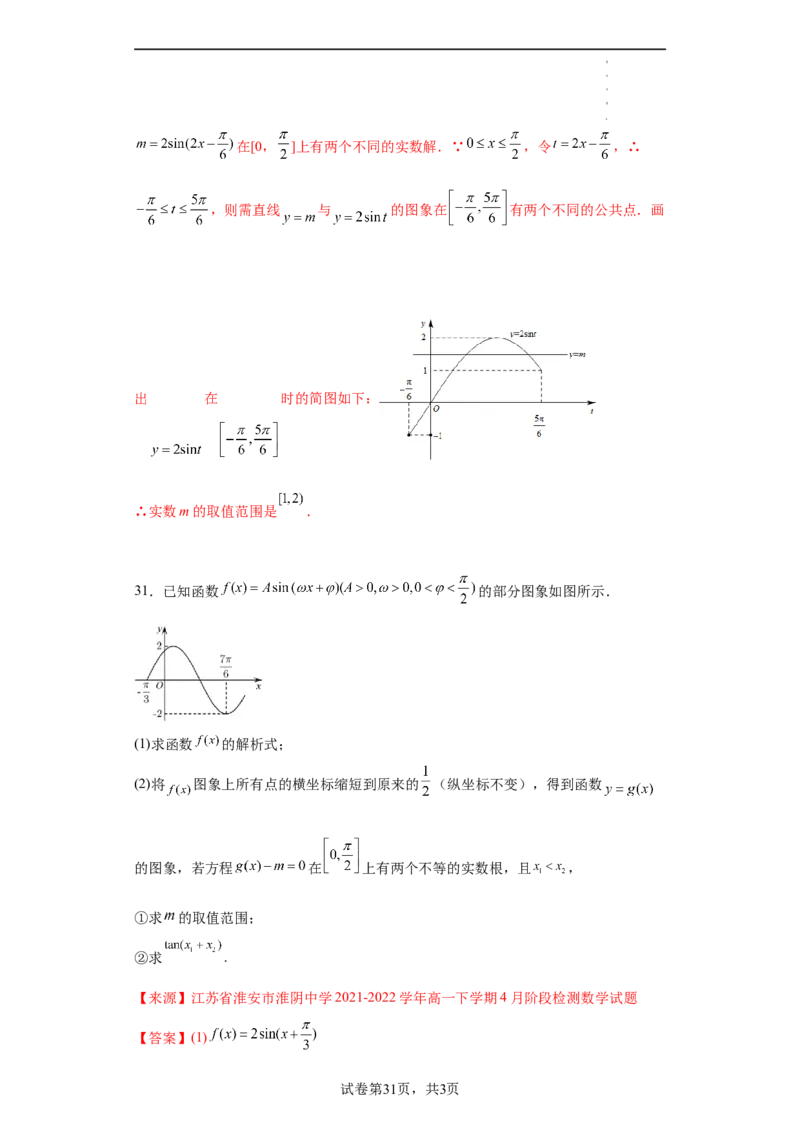
30.已知函数 的部分图象如图.
试卷第29页,共3页
学科网(北京)股份有限公司(1)求f(x)的表达式;
(2)将函数f(x)的图象向右平移 个单位长度得到曲线C,把C上各点的横坐标保持
不变,纵坐标变为原来的2倍得到函数g(x)的图象.若关于x的方程 在
上有两个不同的实数解,求实数m的取值范围.
【来源】陕西省汉中市2021-2022学年高一下学期期末数学试题(A卷)
【答案】(1) (2)
【解析】(1)根据图象,可得 , ,∴ ∴ ,
将 代入f(x),得 ,即 , ,又 ,
∴ ,∴ .
(2)将函数(x)的图象向右平移 个单位长度,得曲线C ,由题得
,∵ 在[0, ]上有两个不同的实数解,∴
试卷第30页,共3页
学科网(北京)股份有限公司在[0, ]上有两个不同的实数解.∵ ,令 ,∴
,则需直线 与 的图象在 有两个不同的公共点.画
出 在 时的简图如下:
∴实数m的取值范围是 .
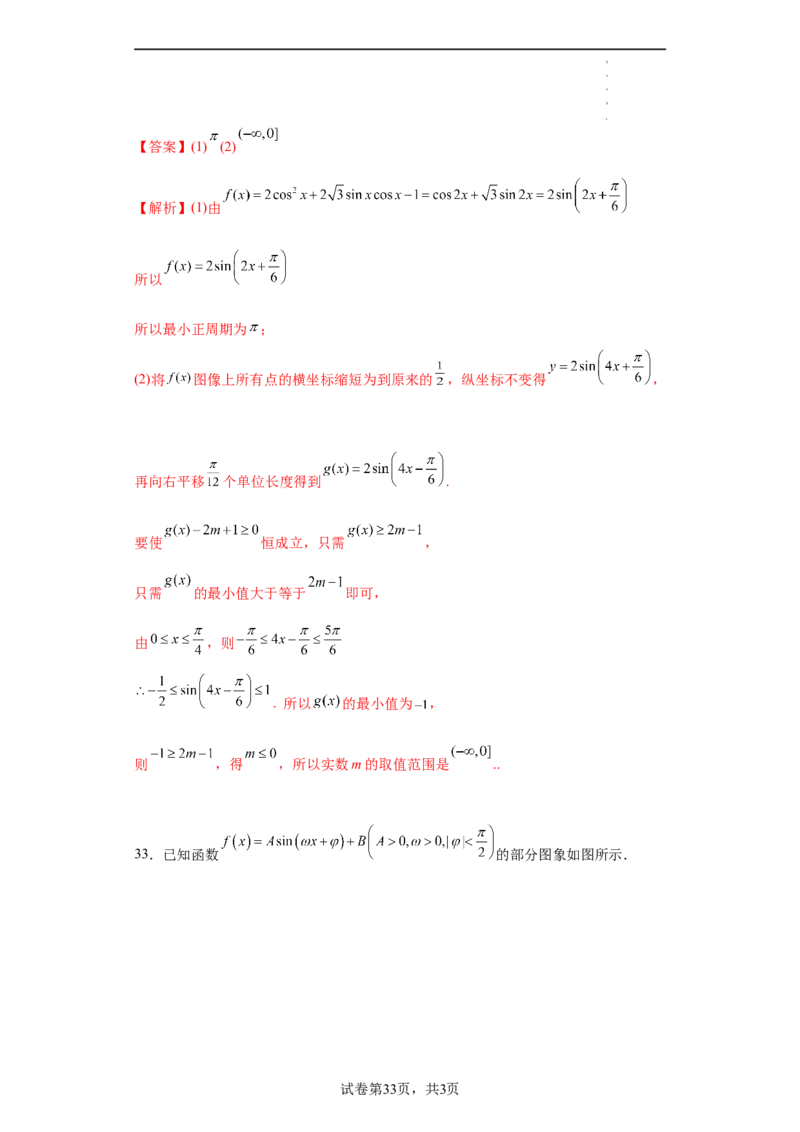
31.已知函数 的部分图象如图所示.
(1)求函数 的解析式;
(2)将 图象上所有点的横坐标缩短到原来的 (纵坐标不变),得到函数
的图象,若方程 在 上有两个不等的实数根,且 ,
①求 的取值范围;
②求 .
【来源】江苏省淮安市淮阴中学2021-2022学年高一下学期4月阶段检测数学试题
【答案】(1)
试卷第31页,共3页
学科网(北京)股份有限公司(2)① ②
【解析】(1)根据函数图像得: , ,
所以 ,所以 ,所以 ,
因为函数图像过点 ,所以 ,所以 ,
所以 .
(2)根据题意,所以 ,
当 时, 单调递增,当 时, 单调递减,
因为 , , ,
所以若 在 上有两个不等的实数根,则 ,
因为函数 关于直线 对称,所以 ,
所以 ,所以 .
32.已知函数 .
(1)求函数 的最小正周期;
(2)现将 图像上所有点的横坐标缩短到原来的 ,纵坐标不变;再向右平移 个单
位长度得到 的图像,若当 时, 恒成立,求实数m的取值
范围.
【来源】贵州省黔东南州2021-2022学年高一下学期期末文化水平测试数学试题
试卷第32页,共3页
学科网(北京)股份有限公司【答案】(1) (2)
【解析】(1)由
所以
所以最小正周期为 ;
(2)将 图像上所有点的横坐标缩短为到原来的 ,纵坐标不变得 ,
再向右平移 个单位长度得到 .
要使 恒成立,只需 ,
只需 的最小值大于等于 即可,
由 ,则
. 所以 的最小值为 ,
则 ,得 ,所以实数m的取值范围是 ..
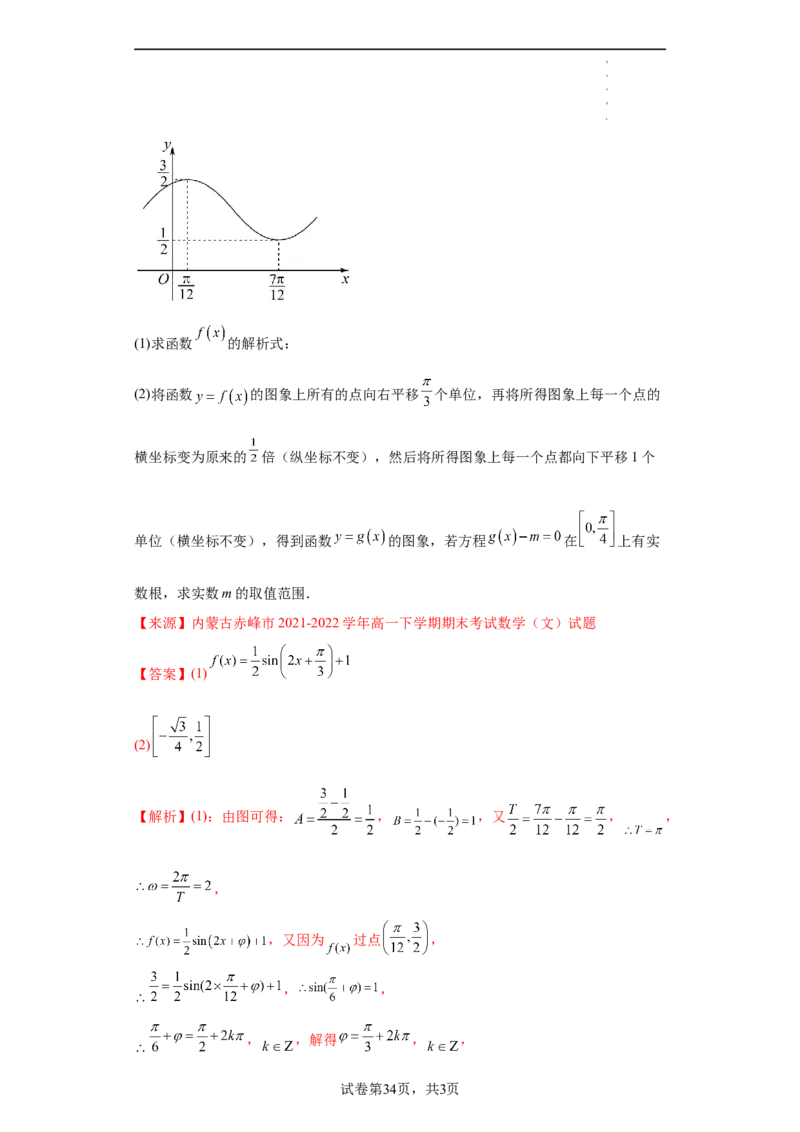
33.已知函数 的部分图象如图所示.
试卷第33页,共3页
学科网(北京)股份有限公司(1)求函数 的解析式:
(2)将函数 的图象上所有的点向右平移 个单位,再将所得图象上每一个点的
横坐标变为原来的 倍(纵坐标不变),然后将所得图象上每一个点都向下平移1个
单位(横坐标不变),得到函数 的图象,若方程 在 上有实
数根,求实数m的取值范围.
【来源】内蒙古赤峰市2021-2022学年高一下学期期末考试数学(文)试题
【答案】(1)
(2)
【解析】(1):由图可得: , ,又 , ,
,
,又因为 过点 ,
, ,
, ,解得 , ,
试卷第34页,共3页
学科网(北京)股份有限公司又 , ,
.
(2):将函数 的图象上所有的点向右平移 个单位得到
,
再将 上每一个点的横坐标变为原来的 倍(纵坐标不变)得到
,
最后将 图象上的每一个点都向下平移1个单位(横坐标不变)得到
,
即 ,
因为 ,所以 ,所以 ,
则 ,
因为方程 在 上有实数根,即 与 在 上有交点,
所以 .
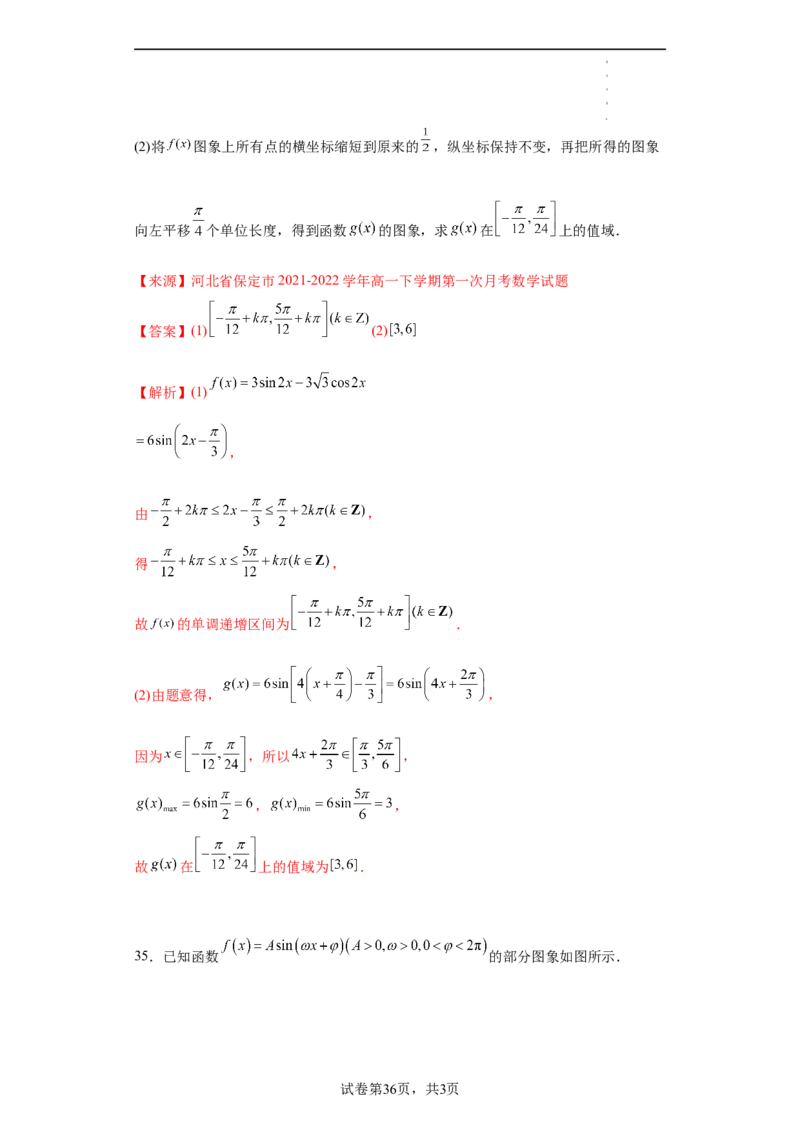
34.已知函数 .
(1)求 的单调递增区间;
试卷第35页,共3页
学科网(北京)股份有限公司(2)将 图象上所有点的横坐标缩短到原来的 ,纵坐标保持不变,再把所得的图象
向左平移 个单位长度,得到函数 的图象,求 在 上的值域.
【来源】河北省保定市2021-2022学年高一下学期第一次月考数学试题
【答案】(1) (2)
【解析】(1)
,
由 ,
得 ,
故 的单调递增区间为 .
(2)由题意得, ,
因为 ,所以 ,
, ,
故 在 上的值域为 .
35.已知函数 的部分图象如图所示.
试卷第36页,共3页
学科网(北京)股份有限公司(1)求函数 的解析式;
(2)若 为偶函数,求t的值;
(3)若 , , 的值域为 ,求实数a,b的值.
【来源】上海市奉贤中学2021-2022学年高一下学期线上教学调研检测数学试题
【答案】(1) ;(2) 或 ;(3) 或 .
【解析】(1)由图可得 , ,
, ,则 ,
又 ,解得 ,
,
, ;
(2) 为偶函数,
,解得 ,
, 或 ;
试卷第37页,共3页
学科网(北京)股份有限公司(3)令 ,
则
,
, ,
∴ ,∴ ,又 的值域为 ,
即 ,显然 ,
∴ 或 ,解得 或 .
试卷第38页,共3页
学科网(北京)股份有限公司试卷第39页,共3页
学科网(北京)股份有限公司