文档内容
专题 5.7 三角函数应用
一、函数y=Asin(ωx+φ)(A>0,ω>0)中,A,ω,φ的物理意义
1.简谐运动的振幅就是A.
2.简谐运动的周期T=.
3.简谐运动的频率f==.
4.ωx+φ称为相位.
5. x=0时的相位φ称为初相.
二、三角函数模型的应用
1.三角函数作为描述现实世界中周期现象的一种数学模型,可以用来研究很多问题,
在刻画周期变化规律、预测其未来等方面都发挥着十分重要的作用.实际问题通常涉
及复杂的数据,因此往往需要使用信息技术.
2.建立函数模型的一般步骤
3.解三角函数应用问题的基本步骤
4.运用三角函数模型解决问题的几种类型
(1)由图象求解析式:首先由图象确定解析式的基本形式,例如:y=Asin(ωx+φ),然
后根据图象特征确定解析式中的字母参数,在求解过程中还要结合函数性质.
(2)由图象研究函数的性质:通过观察分析函数图象,能得出函数的单调性、奇偶性、
对称性、周期性.
(3)利用三角函数研究实际问题:首先分析、归纳实际问题,抽象概括出数学模型,再
利用图象及性质解答数学问题,最后解决实际问题.一、单选题
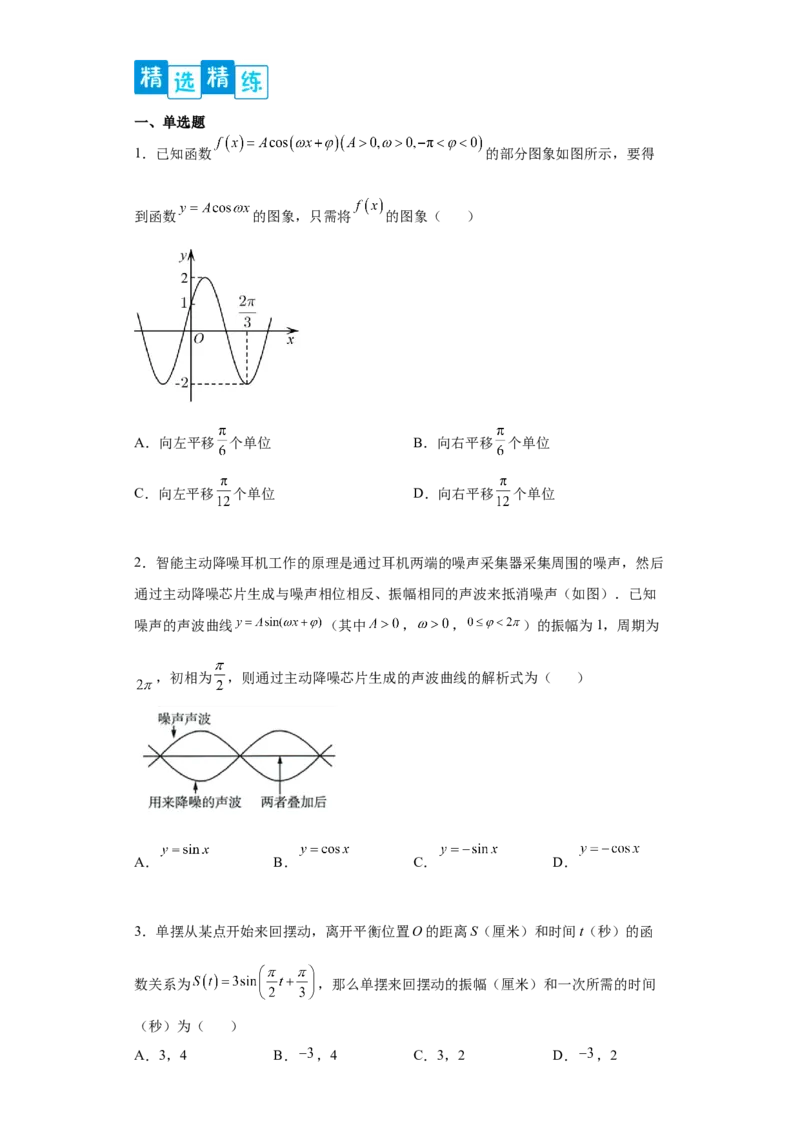
1.已知函数 的部分图象如图所示,要得
到函数 的图象,只需将 的图象( )
A.向左平移 个单位 B.向右平移 个单位
C.向左平移 个单位 D.向右平移 个单位
2.智能主动降噪耳机工作的原理是通过耳机两端的噪声采集器采集周围的噪声,然后
通过主动降噪芯片生成与噪声相位相反、振幅相同的声波来抵消噪声(如图).已知
噪声的声波曲线 (其中 , , )的振幅为1,周期为
,初相为 ,则通过主动降噪芯片生成的声波曲线的解析式为( )
A. B. C. D.
3.单摆从某点开始来回摆动,离开平衡位置O的距离S(厘米)和时间t(秒)的函
数关系为 ,那么单摆来回摆动的振幅(厘米)和一次所需的时间
(秒)为( )
A.3,4 B. ,4 C.3,2 D. ,24.如图为一简谐运动的图象,则下列判断正确的是
A.该质点的振动周期为
B.该质点的振幅为
C.该质点在 和 时的振动速度最大
D.该质点在 和 时的加速度为
5.已知函数 ,为了得到函数 的图象只需将
的图象( )
A.向左平移 个单位 B.向右平移 个单位
C.向左平移 个单位 D.向右平移 个单位
6.已知函数 ,现将 的图向左平移 个单位长度,再将所
得图象上各点的横坐标伸长为原来的 倍,纵坐标不变,得到函数 的图象,则
( )
A. B. C. D.
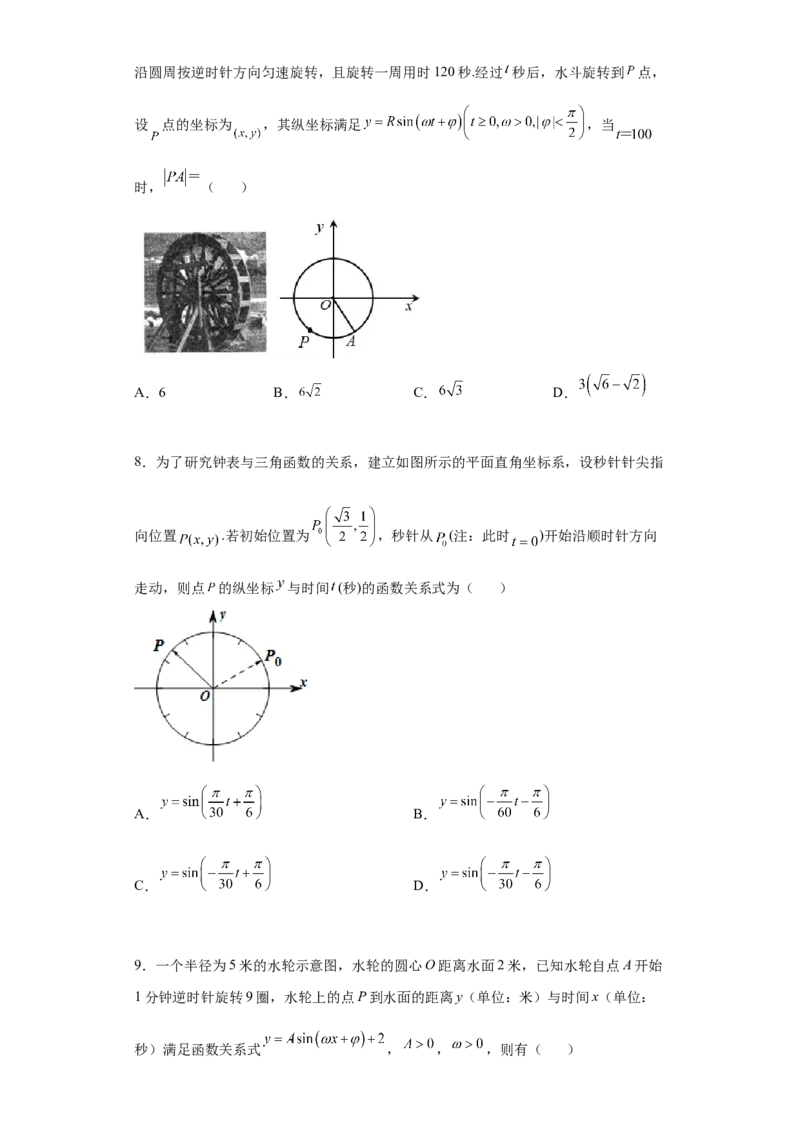
7.水车在古代是进行灌溉引水的工具,是人类的一项古老的发明,也是人类利用自然
和改造自然的象征.如图是一个半径为 的水车,以水车的中心为原点,过水车的中心
且平行于水平面的直线为 轴,建立平面直角坐标系,一个水斗从点 出发,沿圆周按逆时针方向匀速旋转,且旋转一周用时120秒.经过 秒后,水斗旋转到 点,
设 点的坐标为 ,其纵坐标满足 ,当
时, ( )
A.6 B. C. D.
8.为了研究钟表与三角函数的关系,建立如图所示的平面直角坐标系,设秒针针尖指
向位置 .若初始位置为 ,秒针从 (注:此时 )开始沿顺时针方向
走动,则点 的纵坐标 与时间 (秒)的函数关系式为( )
A. B.
C. D.
9.一个半径为5米的水轮示意图,水轮的圆心O距离水面2米,已知水轮自点A开始
1分钟逆时针旋转9圈,水轮上的点P到水面的距离y(单位:米)与时间x(单位:
秒)满足函数关系式 , , ,则有( )A. , B. ,
C. , D. ,
10.已知函数 ,那么下列判断正确的是( )
A.函数 在 上单调递减
B.函数 在 上的最小值为
C.函数 的图象关于直线 对称
D.要得到函数 的图象只需将 的图象向右平移 个单位长度
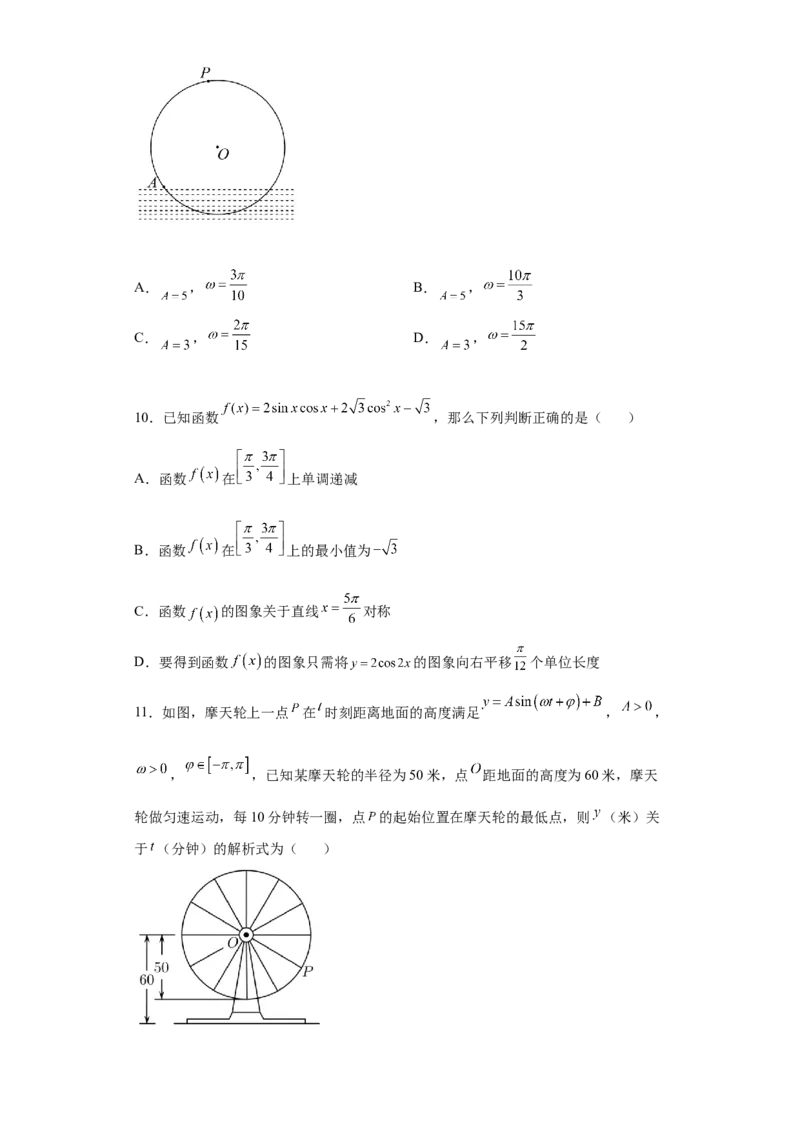
11.如图,摩天轮上一点 在 时刻距离地面的高度满足 , ,
, ,已知某摩天轮的半径为50米,点 距地面的高度为60米,摩天
轮做匀速运动,每10分钟转一圈,点 的起始位置在摩天轮的最低点,则 (米)关
于 (分钟)的解析式为( )A. ( ) B. ( )
C. ( ) D. ( )
12.一半径为 的水轮如图所示,水轮圆心 距离水面 ,已知水轮每 逆时
针转动一圈,如果当水轮上点 从水中浮现时(图中点 )开始计时,则( )
A.点 第一次到达最高点需要
B.在水轮转动的一圈内,点 距离水面的高度不低于 共有 的时间
C.点 距离水面的距离 (单位: )与时间 (单位: )的函数解析式为
D.当水轮转动 时,点 在水面下方,距离水面
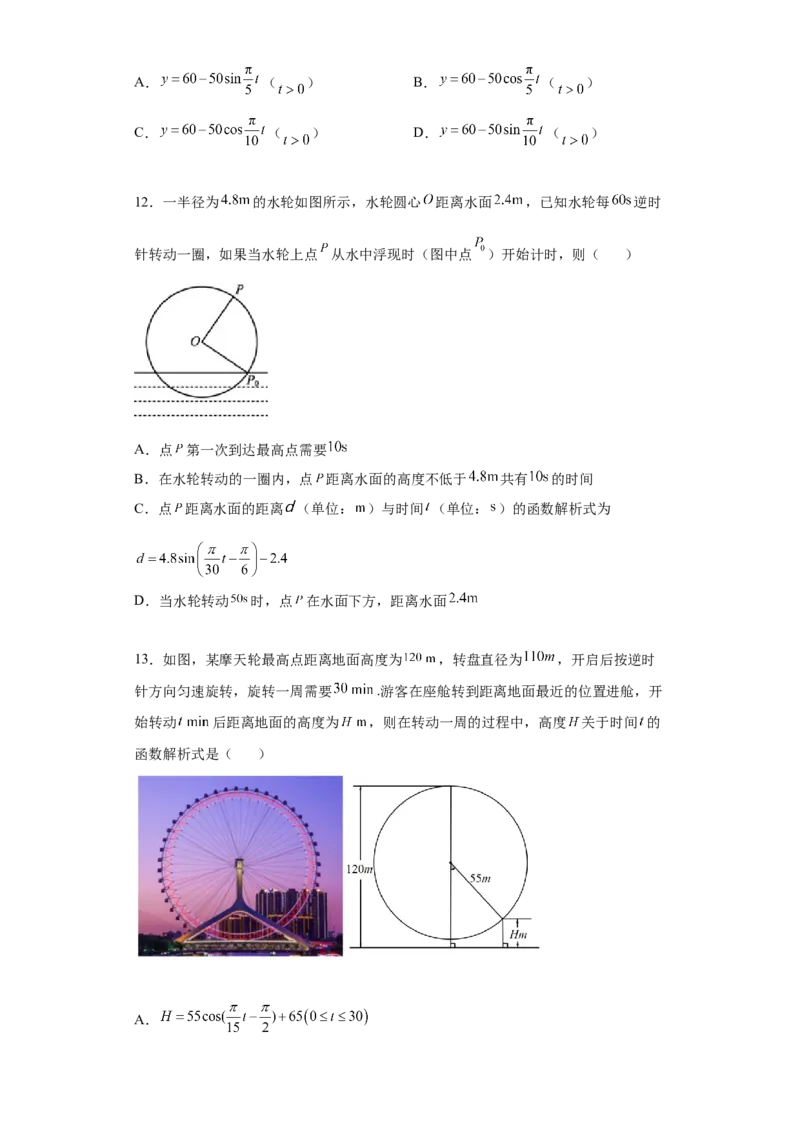
13.如图,某摩天轮最高点距离地面高度为 ,转盘直径为 ,开启后按逆时
针方向匀速旋转,旋转一周需要 .游客在座舱转到距离地面最近的位置进舱,开
始转动 后距离地面的高度为 ,则在转动一周的过程中,高度 关于时间 的
函数解析式是( )
A.B.
C.
D.
14.已知曲线C1:y=cos x,C2:y=sin (2x+ ),则下面结论正确的是
A.把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移
个单位长度,得到曲线C2
B.把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移
个单位长度,得到曲线C2
C.把C1上各点的横坐标缩短到原来的 倍,纵坐标不变,再把得到的曲线向右平移
个单位长度,得到曲线C2
D.把C1上各点的横坐标缩短到原来的 倍,纵坐标不变,再把得到的曲线向左平移
个单位长度,得到曲线C2
15.若函数 的图象向右平移 个长度单位后关于点
对称,则 在 上的最小值为( )
A. B. C. D.
二、多选题
16.对于函数 有( )A. 的图象关于点 对称
B. 的图象过点
C. 的图象是由 的图象向右平移 个单位长度得到的
D. 的图象关于直线 对称
17.已知 ,则下列说法中正确的是( )
A.函数 的最小正周期为
B.函数 在 上单调递减
C. 是函数 图象的一个对称中心
D.函数 的图象可以由函数 图象上各点的纵坐标不变,横坐
标缩小为原来的 得到
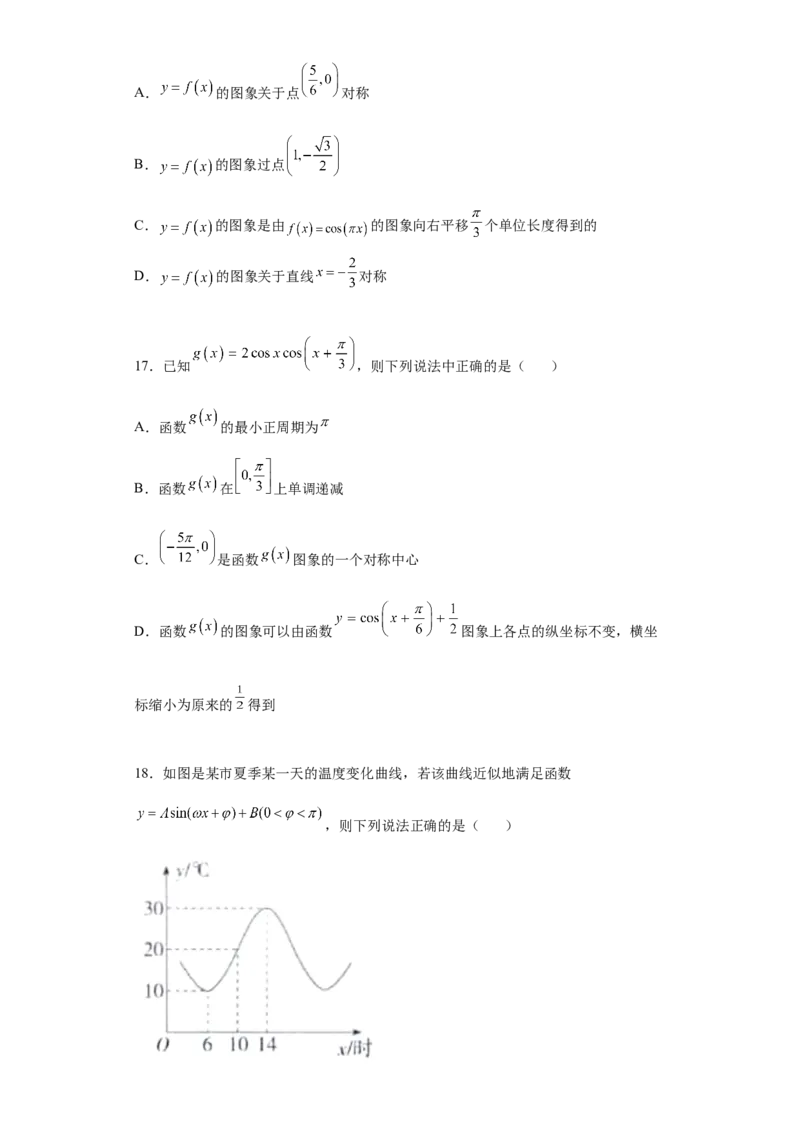
18.如图是某市夏季某一天的温度变化曲线,若该曲线近似地满足函数
,则下列说法正确的是( )A.该函数的周期是16
B.该函数图象的一条对称轴是直线
C.该函数的解析式是
D.这一天的函数关系式也适用于第二天
E.该市这一天中午12时天气的温度大约是27℃
19.已知函数 (a为常数, )的图像关于直线 对称,函
数 ,则下面说法正确的是( )
A.将 的图像向左平移 个单位可以得到 的图像
B. 的图像关于点 对称
C. 在 上单调递减
D. 的最大值为1
20.函数 ,其图象的一个最高点是 ,距
离 点最近的对称中心为 ,则( )
A.
B. 时,函数 单调递增
C. 是函数 图象的一条对称轴
D. 图象向右平移 个单位后得到 的图象,若 是奇函数,则 的
最小值是21.将函数 的图像向左平移 ( )个单位,得到函数 的图像,
若函数 是偶函数,则 的可能取值为( )
A. B. C. D.
三、解答题
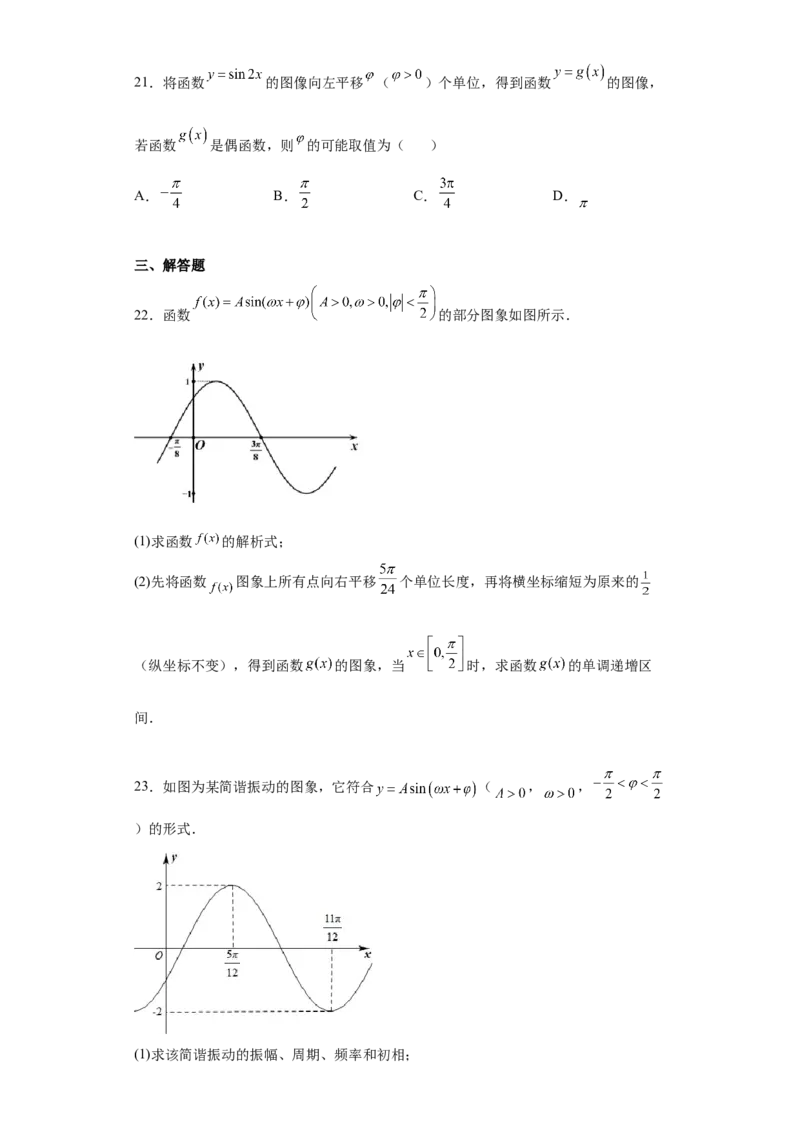
22.函数 的部分图象如图所示.
(1)求函数 的解析式;
(2)先将函数 图象上所有点向右平移 个单位长度,再将横坐标缩短为原来的
(纵坐标不变),得到函数 的图象,当 时,求函数 的单调递增区
间.
23.如图为某简谐振动的图象,它符合 ( , ,
)的形式.
(1)求该简谐振动的振幅、周期、频率和初相;(2)求该简谐振动的函数解析式;
(3)求该函数的单调递增区间.
24.已知函数 , 的图像先向右平移 ,再纵
坐标不变横坐标伸长为原来的2倍,得到 的图像.
(1)求 的对称中心;
(2)当 时,求 的取值范围
25.已知函数 满足下列3个条件:
①函数 的周期为 ;② 是函数 的对称轴;③ .
(1)请任选其中二个条件,并求出此时函数 的解析式;
(2)若 ,求函数 的最值.
26.已知函数 .
(Ⅰ)求 的最小正周期:
(Ⅱ)求 在区间 上的最大值和最小值.