文档内容
专题 7.2 离散型随机变量及其分布列
姓名: 班级:
重点 离散型随机变量的概念
难点 分布列的概念
[多选]例1-1.下列叙述中,是随机变量的有( )。
A、某工厂加工的零件,实际尺寸与规定尺寸之差
B、标准状态下,水沸腾的温度
C、某大桥一天经过的车辆数
D、向平面上投掷一点,此点坐标
【答案】ACD
【解析】标准状态下,水沸腾的温度为 ,为常数,其他均为变量,故选ACD。
例1-2.下列叙述中,是离散型随机变量的为( )。
A、某人早晨在车站等出租车的时间
B、将一颗均匀硬币掷十次,出现正面或反面的次数
C、连续不断的射击,首次命中目标所需要的次数
D、袋中有 个黑球 个红球,任取 个,取得一个红球的可能性
【答案】C
【解析】A选项是随机变量,但不能一一列出,不是离散型,
B选项掷硬币不是正面就是反面,次数之和为十,是常量,
D选项事件发生的可能性不是随机变量,
故选C。
例1-3.如果 是一个离散型随机变量,那么下列命题中假命题是( )。
A、 取每一个可能值的概率是非负实数
B、 取所有可能值的概率和为
C、 取某两个可能值的概率等于取其中每个值的概率之和
D、 在某一范围内取值的概率大于它取这个范围内各个值的概率之和
【答案】D
【解析】根据离散型随机变量的分布列的性质,每一个变量对应的概率都非负,
所有变量对应的概率之和是 ,每一个变量对应的事件是互斥事件,
取某两个可能值的慨率等于分别取其中每个值的概率之和,
得到A、B、C三个说法都正确,故选D。
例1-4.下列 个表格中,可以作为离散型随机变量分布列的一个是( )。
A、B、
C、
D、
【答案】C
【解析】根据离散型随机变量的分布列的性质检验即可。
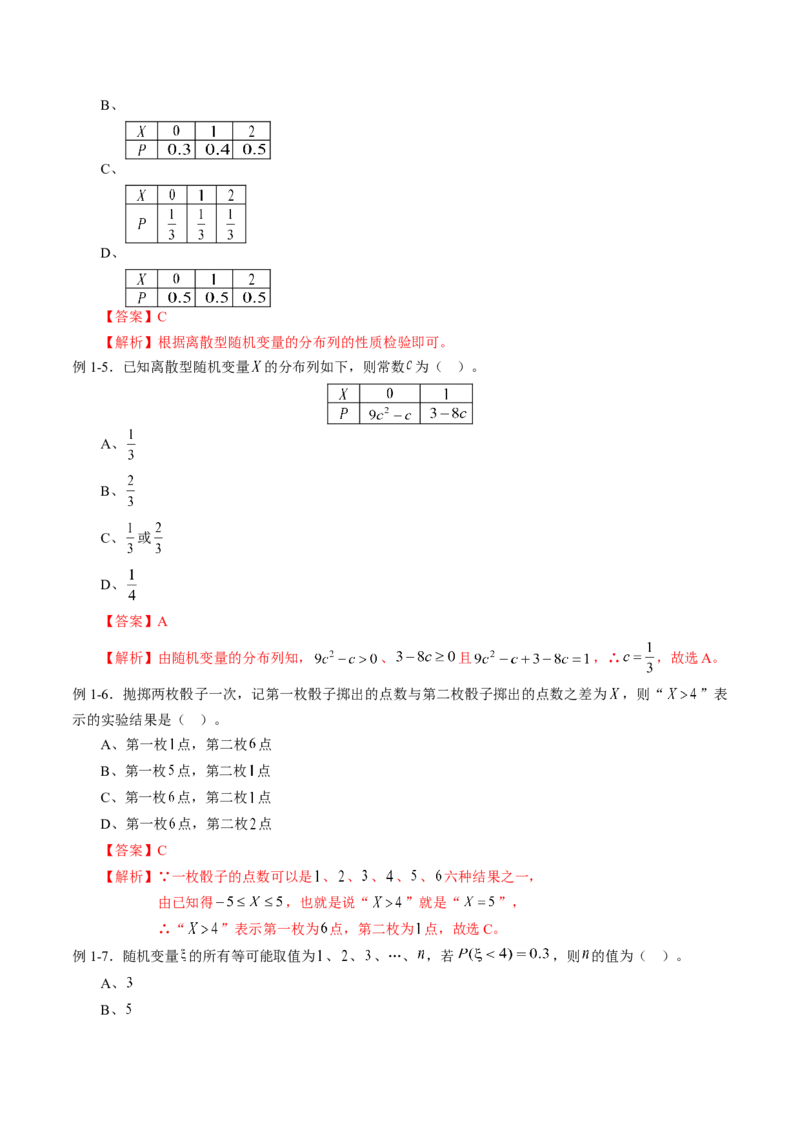
例1-5.已知离散型随机变量 的分布列如下,则常数 为( )。
A、
B、
C、 或
D、
【答案】A
【解析】由随机变量的分布列知, 、 且 ,∴ ,故选A。
例1-6.抛掷两枚骰子一次,记第一枚骰子掷出的点数与第二枚骰子掷出的点数之差为 ,则“ ”表
示的实验结果是( )。
A、第一枚 点,第二枚 点
B、第一枚 点,第二枚 点
C、第一枚 点,第二枚 点
D、第一枚 点,第二枚 点
【答案】C
【解析】∵一枚骰子的点数可以是 、 、 、 、 、 六种结果之一,
由已知得 ,也就是说“ ”就是“ ”,
∴“ ”表示第一枚为 点,第二枚为 点,故选C。
例1-7.随机变量 的所有等可能取值为 、 、 、…、 ,若 ,则 的值为( )。
A、
B、C、
D、
【答案】D
【解析】∵ ,
∴ ,而 , ,故选
D。
例1-8.抛掷两颗骰子,所得点数之和记为 ,那么 表示的随机试验结果是( )。
A、两颗都是 点
B、两颗都是 点
C、一颗是 点,另一颗是 点
D、一颗是 点,另一颗是 点,或者两颗都是 点
【答案】D
【解析】由于抛掷一颗骰子,可能出现的点数是 、 、 、 、 、 这 种情况之一,
而 表示抛掷两颗骰子所得点数之和,∴ ,
表示的随机试验结果是:一颗是 点,另一颗是 点,或者两颗都是 点,故选D。
例1-9.设 是一个离散型随机变量,则下列不一定能成为 的概率分布列的一组数是( )。
A、 , , ,
B、 , , ,
C、 , ( 为实数)
D、 , ,…, , ( 且 )
【答案】C
【解析】显然A、B满足分布列的两个性质,
对于D,有 ,又 、 ,
且 ,
∴它也满足分布列性质,
C中,由于 为实数,不妨取 ,显然 不满足概率的非负性,
故选C。
例1-10.一个人有 把钥匙,其中只有一把可以打开房门,他随意的进行试开,若试开过的钥匙放在一边,
试开次数 为随机变量,则 ( )。
A、
B、C、
D、
【答案】A
【解析】事件 表示前 次没打开,第 次打开了,
∴ ,故选A。
例1-11.抛掷两枚骰子一次,设 为第一枚骰子与第二枚骰子的点数之差,则它的所有可能取值为( )。
A、 ,
B、 ,
C、 ,
D、 ,
【答案】D
【解析】抛掷一枚骰子出现的最小点数为 ,最大点数为 ,∴ , ,故选D。
例1-12.某电子管正品率为 ,次品率为 ,现对该批电子管进行测试,设第 ξ次首次测到正品,则
( )。
A、
B、
C、
D、
【答案】B
【解析】 表示第 次首次测到正品,而前两次都没有测到正品,
则其概率是 ,故选B。
例1-13.袋中有大小相同的红球 个,白球 个,从袋中每次任取一球(不放回),直到取出球是白球为
止,取球次数是一个随机变量,这个随机变量的值域为 。
【答案】
【解析】最少取一次,最多将 个红球取完,第 次取得白球。
例1-14.设随机变量 的分布列为 , 或 ,则 。
【答案】【解析】由题意, ,且 ,解得 。
例1-15.写出下列随机变量可能取的值,并说明随机变量所取的值表示的随机试验的结果。
(1)一袋中装有 只同样大小的白球,编号为 、 、 、 、 。现从该袋内随机取出 只球,被取出的
球的最大号码数 ;
(2)某单位的某部电话在单位时间内收到的呼叫次数 。
【解析】(1) 可取 、 、 ,
,表示取出的 个球的编号为: 、 、 ,
,表示取出的 个球的编号为: 、 、 或 、 、 或 、 、 ,
,表示取出的 个球的编号为:
、 、 或 、 、 或 、 、 或 、 、 或 、 、 或 、 、 ;
(2) 可取 、 、 、…、 , ,表示被呼叫 次,其中 、 、 、…。