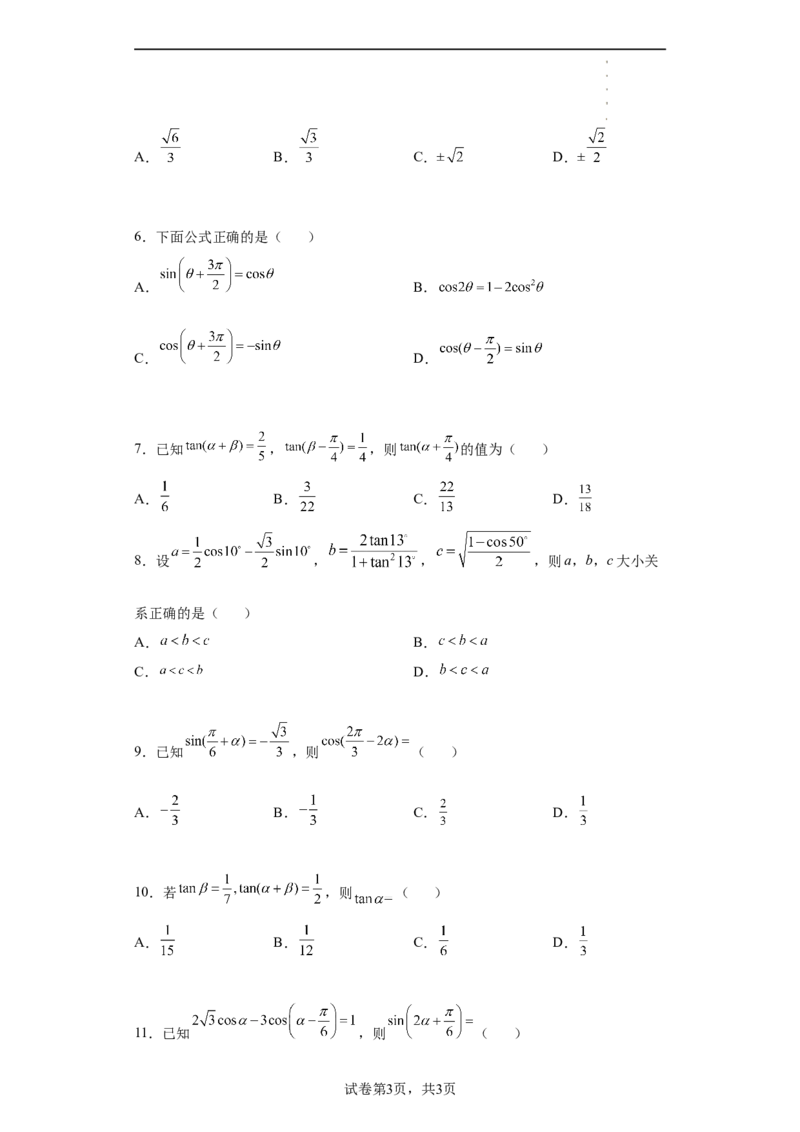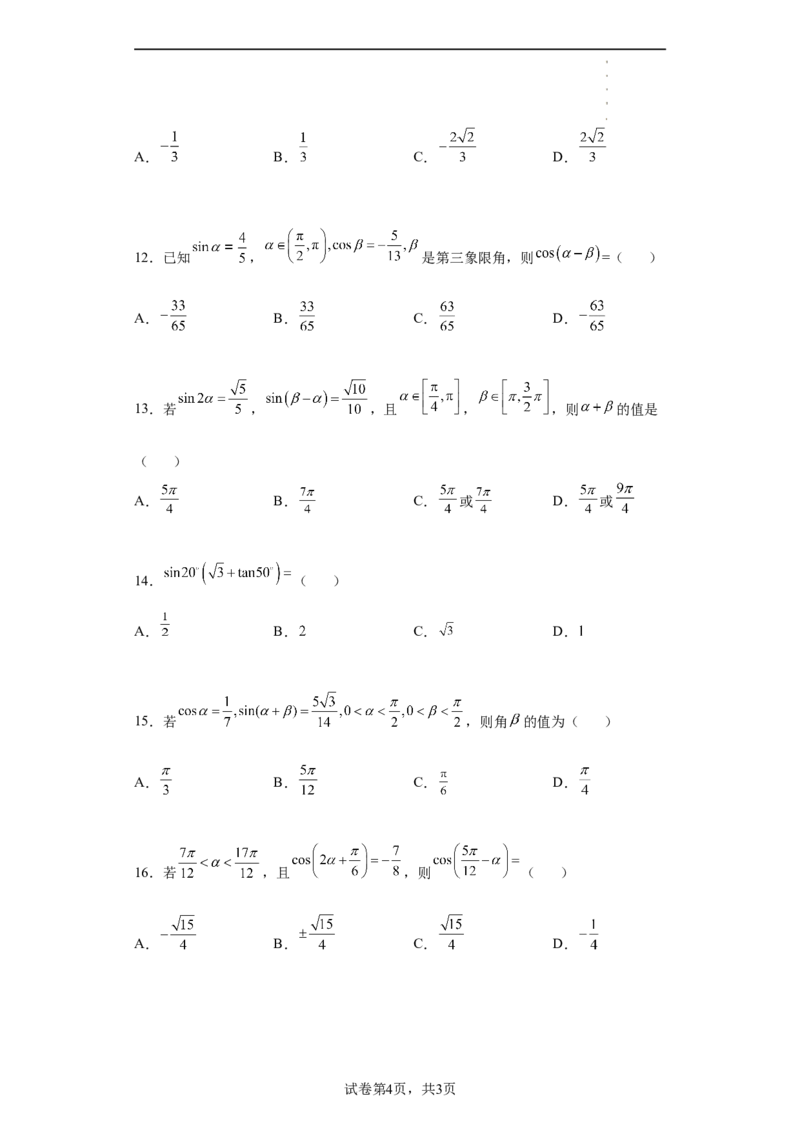专题5.5三角恒等变换（原卷版）_E015高中全科试卷_数学试题_必修1_05.复习精选精练2023年

专题 5.5 三角恒等变换 （一）两角和与差的正弦、余弦、正切公式 1．C ：cos(α－β)＝cosαcosβ＋sinαsinβ； (α－β) C ：cos(α＋β)＝cosαcos_β－sin_αsinβ； (α＋β) S ：sin(α＋β)＝sinαcosβ＋cosαsinβ； (α＋β) S ：sin(α－β)＝sin_αcos_β－cosαsinβ； (α－β) T ：tan(α＋β)＝； (α＋β) T ：tan(α－β)＝. (α－β) 2．变形公式： tan α±tan β＝tan(α±β)(1 tanαtanβ)；  sincos 2sin(∓ ) 4 . sinαsinβ＋cos(α＋β)＝cosαcosβ， cosαsinβ＋sin(α－β)＝sinαcosβ， 3．辅助角公式： 函数f(α)＝acos α＋bsin α(a，b为常数)，可以化为f(α)＝sin(α＋φ)或f(α)＝cos(α－φ)， 其中φ可由a，b的值唯一确定． （二）二倍角的正弦、余弦、正切公式 1.S ：sin 2α＝2sinαcosα； 2α C ：cos 2α＝cos2α－sin2α＝2cos2α－1＝1－2sin2α； 2α T ：tan 2α＝. 2α 2.变形公式： （1）降幂公式：cos2α＝，sin2α＝，sin αcos α＝sin 2α. （2）升幂公式 1＋cos α＝2cos2； 1－cos α＝2sin2； 1＋sin α＝； 1－sin α＝. （3）配方变形：1＋sin 2α＝(sin α＋cos α)2,1－sin 2α＝(sin α－cos α)2 1±sinα＝2,1＋cosα＝2cos2，1－cosα＝2sin2 （4）sin 2α＝＝； cos 2α＝＝. tan ＝＝. （三）常见变换规律(1)角的变换：明确各个角之间的关系(包括非特殊角与特殊角、已知角与未知角)，熟 悉角的变换技巧，及半角与倍角的相互转化，如：2α＝(α＋β)＋(α－β)，α＝(α＋β)－β ＝(α－β)＋β，40°＝60°－20°，＋＝，＝2×等． (2)名的变换：明确各个三角函数名称之间的联系，常常用到同角关系、诱导公式，把 正弦、余弦化为正切，或者把正切化为正弦、余弦． 一、单选题 1． 等于（ ） A． B．1 C．0 D． 2．已知 ，且 ，则 的值为（ ） A． B． C． D． 3．已知 均为锐角，且 ，则 （ ） A． B． C． D． 4．已知 ， ，则 的值为（ ） A．2 B． C． D． 5．已知 ，则 （ ） 试卷第2页，共3页 学科网（北京）股份有限公司A． B． C．± D．± 6．下面公式正确的是（ ） A． B． C． D． 7．已知 ， ，则 的值为（ ） A． B． C． D． 8．设 ， ， ，则a，b，c大小关 系正确的是（ ） A． B． C． D． 9．已知 ，则 （ ） A． B． C． D． 10．若 ，则 （ ） A． B． C． D． 11．已知 ，则 （ ） 试卷第3页，共3页 学科网（北京）股份有限公司A． B． C． D． 12．已知 ， 是第三象限角，则 =（ ） A． B． C． D． 13．若 ， ，且 ， ，则 的值是 （ ） A． B． C． 或 D． 或 14． （ ） A． B． C． D． 15．若 ，则角 的值为（ ） A． B． C． D． 16．若 ，且 ，则 （ ） A． B． C． D． 试卷第4页，共3页 学科网（北京）股份有限公司17．已知 ， ，则 （ ） A． B． C． D． 18．若 ，则 （ ） A． B． C． D． 19．已知 ，则 的值是（ ） A． B． C． D． 20．已知 ，且 ，则 （ ） A． B． C． D． 二、多选题 21．对于函数 ，下列结论正确的是（ ） A． 的最小正周期为 B． 的最小值为 试卷第5页，共3页 学科网（北京）股份有限公司C． 的图象关于直线 对称 D． 在区间 上单调递增 22．下列各式中，值为 的是（ ） A． B． C． D． 23．已知函数 ，则下列结论正确的有（ ） A． 的最小正周期为 B．直线 是 图象的一条对称轴 C． 在 上单调递增 D．若 在区间 上的最大值为 ，则 24．已知函数 的周期为 ，当 时， 的（ ） A．最小值为 B．最大值为 C．零点为 D．增区间为 25．关于函数 ，下列命题正确的是（ ） A．若 ， 满足 ，则 成立； 试卷第6页，共3页 学科网（北京）股份有限公司B． 在区间 上单调递增； C．函数 的图象关于点 成中心对称； D．将函数 的图象向左平移 个单位后将与 的图象重合． 三、解答题 26．求下列各式的值 (1) (2) (3) (4) . 27．已知 ，其中 . (1)求 ； (2)若 ，求 的值. 28．已知角 为锐角， ，且满足 ， (1)证明： ； (2)求 . 试卷第7页，共3页 学科网（北京）股份有限公司29．已知 ， 为锐角， ， ． (1)求 的值； (2)求角 ． 30．已知 (1)求 的值； (2)若 都是锐角， ，求 的值. 31．已知 是方程 的两根，求下列各式的值： (1) (2) ； (3) . 试卷第8页，共3页 学科网（北京）股份有限公司试卷第9页，共3页 学科网（北京）股份有限公司